基于矢量位和标量位的空间波数混合域电磁三维正演模拟

2022-01-25戴世坤赵东东1李昆张钱江凌嘉宣陈轻蕊

地球物理学报 2022年1期

戴世坤,赵东东1,*,李昆,张钱江,凌嘉宣,陈轻蕊

1 桂林电子科技大学电子工程与自动化学院，桂林 541004 2 中南大学有色金属成矿预测与地质环境监测教育部重点实验室,长沙 410083 3 中南大学地球科学与信息物理学院,长沙 410083 4 桂林理工大学地球科学学院,桂林 541004

0 引言

电磁法是地球物理勘探中相对成熟的方法之一，目前已经广泛应用于深部地质结构(Brasse and Soyer,2001;Unsworth et al.,2005;Becken et al.,2011)、金属矿产资源(Zhdanov,2010;Smith,2014)、地下水和地热(周厚芳等,2003;黄力军等,2004;Pedersen et al.,2006)及工程和环境勘察等领域(Tezkan et al.,2005;Ren et al.,2013).在三维电磁问题中，正演计算速度是影响反演成像效率与人机交互定量解释的关键因素.因此，大规模条件下高效、高精度电磁三维数值模拟方法仍然是当前电磁勘探的主要研究焦点之一.

目前，有关频率域电磁法三维正演方法的研究已经超过了30年(Varentsov,1983;Wannamaker et al.,1984)，并取得了很大的进展.从求解方法的角度(汤井田等,2007)而言，目前常用的电磁三维数值模拟方法主要分为直接解法和间接解法.其中,直接解法(Mackie et al.,1994;Newman and Alumbaugh,1995;Sasaki,2001;Nam et al.,2007)是对电磁场强度的旋度方程再求旋度，求解二阶偏微分方程得到电磁场分布.该方法存在两个问题(Pinchuk et al.,1988;Lynch and Paulsen,1991;Jin,2014)：一是只利用了场矢量的旋度，对散度没有规范，存在“伪解现象”；二是电场在界面上的法向分量不连续，与节点有限元对函数在求解区域内连续这一基本假设相互矛盾.一些学者在直接解法过程中通过(Mackie et al.,1994;Smith,1996;Kordy et al.,2016)引入散度条件和矢量有限单元法(Jin,2014;Sugeng,1998;Zunoubi et al.,1999;Mukherjee and Everett,2011;李勇等,2017)有效解决了以上问题.间接解法是先求取电磁场的势函数，进而通过差分格式求解电磁场，主要包括不加规范的矢量位标量位解法(Mukherjee and Everett,2011;Ansari and Farquharson,2014)，基于库仑条件的矢量位和标量位解法(Haber et al.,2000;Badea et al.,2001;Jahandari and Farquharson,2015)，基于洛伦兹规范的矢量位和标量位解法(Um et al.,2010)和基于轴向规范的矢量位和标量位解法(Varilsüha and Candansayar,2018).Varilsüha和Candansayar(2018)利用有限差分算法实现了以上直接解法与四种间接解法，并对比分析了它们的计算精度及计算速度.从数值方法的角度而言，目前常用的电磁三维数值模拟方法主要包括积分方程法(Hohmann,1975;Lajoie and West,1976;Newman and Hohmann,1988;Avdeev et al.,2002;Hursán and Zhdanov,2002;Zhdanov et al.,2006;Avdeev and Knizhnik,2009)、有限差分法(Mackie et al.,1994;Newman and Alumbaugh,1995;Weiss and Newman,2003;沈金松,2003;Streich,2009;殷长春等,2014;赵宁等,2017)、有限体积法(Haber et al.,2000;Haber and Ascher,2001;Weiss and Constable,2006;杨波等,2012;Jahandari and Farquharson,2014,2015;韩波等,2015)、有限单元法(Badea et al.,2001;Mitsuhata and Uchida,2004;Börner et al.,2008;徐志锋和吴小平,2010;Schwarzbach et al.,2011;Farquharson and Miensopust,2011;Ansari and Farquharson,2014;Grayver and Bürg,2014;杨军等,2015;蔡红柱等,2015 )和谱元法(Lee et al.,2006;刘玲等,2018;陈汉波等,2019)等.总体来讲，国内外相关学者关于电磁三维正演算法研究的核心仍然在于保持较高精度的同时，如何提高计算效率.

为了提高电磁三维数值模拟的计算效率，本文提出一种新的空间波数混合域电磁场三维数值模拟方法.该方法从基于矢量位和标量位耦合偏微分方程(Badea et al.,2001)出发，沿水平方向进行二维傅里叶变换，得到空间波数混合域耦合常微分方程组.采用基于二次插值的一维有限单元法求解该耦合方程组，不同波数之间的耦合方程组相互独立，具有高度并行性.该方法通过二维傅里叶变换将一个大问题拆分为多个小问题，避免了大型稀疏复线性方程组的求解，充分利用追赶法求解定带宽线性方程组的高效性和算法本身的并行性提高了数值模拟效率，减少了内存占用空间，为实现大规模、精细三维数值模拟与反演成像提供了一种新的思路.

1 理论方法

1.1 基于矢量位和标量位控制方程

在频率域，假设时间常数为e-iω t，电磁场满足如下麦克斯韦方程组：

(1)

(2)

上两式中，ω为角频率，i为虚数单位，μ0为真空中磁导率，σ为电导率，ε为介电常数，JS为外加源项，E为电场强度，H为磁场强度.B=μ0H为磁感应强度，通过磁导率与磁场强度H建立联系.

根据磁矢量位和电标量位的关系式(Biro and Preis,1989)

(3)

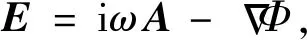
(4)

将式(3)—(4)代入式(2)中，可以得到关于矢量位和标量位的双旋度方程:

(6)

将麦克斯韦方程式(2)代入(6)式,有

(7)

其中，J=JS+σE.进而可以得到

(8)

根据式(4)中电场和矢量位及标量位的关系，将上式(8)进一步化简可得

(9)

式(6)和式(9)即为基于库仑规范的矢量位和标量位耦合方程组(Haber et al.,2000)：

(10)

该方程组在理论上比较完备，物理意义比较明确，通过改变发射场源和频率，基于库仑规范的矢量位和标量位控制方程可以适用于天然场源电磁法(例如大地电磁法，MT)、直流电阻率法(DC)和人工源电磁法(CSEM)三维数值模拟.本文在这里重点研究MT和CSEM三维数值模拟.

1.2 基于二次场的矢量位标量位控制方程

为了避免发射源对异常场的影响，这里把电磁场分解为一次场和二次场.那么基于库仑规范的矢量位和标量位表示为

(11)

其中，Ap,As分别为一次场矢量位和二次场矢量位，Φp,Φs分别为一次场标量位和二次场标量位.

(12)

(13)

式(13)右端项中的总场由一次场和二次场构成E=Ep+Es,一次场Ep是根据均匀层状介质中的电磁场公式计算得到(欧阳芳等，2016),二次场Es是由下文紧算子迭代格式部分的式(29)得到.其中，背景电导率模型一般设置为均匀半空间模型或均匀层状介质模型.

许多学者(Haber et al.,2000;Badea et al.,2001;Jahandari and Farquharson,2015)利用数值方法针对上述方程(10)或(13)的类似表达式进行了模拟，取得了不错的效果.但是由于直接求解大型稀疏矩阵线性方程组，计算量和存储量较大(Varilsüha and Candansayar,2018).为了提高数值模拟效率，充分发挥基于矢量位和标量位控制方程的优势，本文拟针对矢量位和标量位满足的耦合方程组(13)，提出一种空间波数混合域电磁快速三维数值模拟方法.该方法将式(13)沿水平方向进行基于水平网格扩边的快速傅里叶变换或高斯傅里叶变换(Wu and Tian,2014)，有效避免由于快速傅里叶变换引起的强制周期化、边界截断效应的影响.这样就把一个空间域三维偏微分方程转换为多个空间波数混合域一维耦合常微分方程，不同波数之间的耦合常微分方程组相互独立，具有高度并行性.

1.3 空间波数混合域矢量位标量位常微分方程

将式(13)写为分量形式并展开，有

(14)

对于式(14)沿x和y方向进行二维傅里叶变换：

(15)

利用二维傅里叶变换把三维偏微分耦合方程组(14)转化为一维常微分耦合方程组(15)，由此将一个超大规模问题分解为多个小问题，大大减少了对计算时间和存储的需求，且不同波数之间常微分方程组相互独立，具有高度并行性.

1.4 边界条件

(16)

(17)

1.5 有限单元法

(18)

式中，Ne为垂向单元剖分个数，Ni(i=j,p,m)为第e个单元第i个节点的二次插值函数(徐世浙,1994).针对式(18)中主要包含七种类型的积分(详见附录A)，将每一项单元积分进行总体合成，可以得到带宽为23的对角方程组

Ku=P，

(19)

式中，K是23对角矩阵，P是源项，u为待求的空间波数混合域矢量位和标量位.针对该线性方程组，采用追赶法即可实现快速求解.本文采用的数值模拟方法将三维问题转换为多个相互独立的一维问题进行求解，从根本上改变了方程组的特点和求解方式，与迭代解法和直接解法求解大型稀疏复线性方程组相比，追赶法求解常微分方程具有高度并行性，大大降低了计算时间和内存耗费.

1.6 空间波数混合域电磁场分量的计算

为了进一步求取空间波数混合域电磁场分量，须建立矢量位、标量位及电磁场分量之间的关系.将式(4)表示为分量形式：

(20)

针对式(20)沿水平方向进行二维傅里叶变换，即得到空间波数混合域矢量位、标量位与电场分量的关系：

(21)

将式(3)表示为分量形式：

(22)

针对式(22)沿水平方向进行二维傅里叶变换，即得到空间波数混合域矢量位、标量位与磁场分量的关系为

(23)

上式(21)和(23)中涉及的求导运算采用五点差分计算得到，对式(21)和(23)做二维傅里叶反变换，即可得到空间域电磁场.

1.7 紧算子迭代格式

对于上式(18)中矢量位和标量位满足的一维常微分耦合方程组，采用有限单元法求解得到的是Born近似解，直接进行迭代难以实现稳定收敛，甚至发散.针对收敛性问题，这里给出了一种迭代法计算电磁场的方法，其核心是构造一个稳定收敛的迭代算子.

定义一个线性算子

G(·)=G(Δσ·E)，

(24)

可将电场(24)式写为

E=Eb+G(Δσ·E)，

(25)

对于上式(25)，理论上可以采用迭代法逐次逼近进行求解，即可以写为

E(n)=Eb+G(Δσ·E(n-1)).

(26)

由泛函分析中的Banach定理可知，要使得式(26)收敛的条件是

‖G(Δσ·(E(n-1)-E(n)))‖<κ‖Δσ·(E(n-1)-E(n))‖，

(27)

式中κ<1，‖·‖表示2-范数，使得上式成立的条件是

‖G‖<1.

(28)

算子必须是紧算子.Gao(2005)从能量不等式出发，对算子G进行了修正，构造了满足式(28)的迭代格式，迭代格式如下：

(29)

式中α,β是与背景场电导率σb、异常体电导率与背景场电导率的差Δσ有关的张量：

(30)

(31)

2 数值试验

设计棱柱体模型用于验证空间波数混合域(mixed space-wavenumber domain,MSWD)电磁场三维数值模拟算法的正确性、计算精度和计算效率.由于大地电磁法(MT)和可控源电磁法(CSEM)对应的源项处理和背景场不同，计算精度不尽相同，但并不影响计算效率的统计，故数值试验部分主要分为：①大地电磁场(MT)计算精度；②可控源电磁场(CSEM)计算精度；③计算效率.

2.1 大地电磁场计算精度

设计如下图1所示的棱柱体模型，用于验证空间波数混合域大地电磁场三维数值模拟算法(MSWD)的正确性和计算精度.模型参数为：空气层电阻率为1.0×108Ωm,均匀半空间模型背景电阻率为100 Ωm,棱柱体电阻率为10 Ωm,其大小为0.4 km×0.4 km×0.4 km,顶面埋深为0.2 km;模拟区域大小为2 km×2 km,模拟区域网格节点剖分为51×51×71,空气层网格剖分为11层,空间水平采样间隔均为40 m,垂向采用间隔为10 m;发射频率为0.01 Hz、0.1 Hz、1 Hz、10 Hz.首先,采用本文空间波数混合域大地电磁场三维数值模拟算法(MSWD)计算了视电阻率和相位,紧算子迭代次数为15次，稳定收敛，且前后两次迭代的电磁场拟合误差<0.1%;其次,采用传统积分方程(IE)大地电磁场(MT)算法(Zhdanov et al.,2006)计算了视电阻率和相位,并将其近似为参考场;最后,计算了两种算法视电阻率和相位相对误差.

图1 棱柱体模型示意图Fig.1 The sketch of prism model

图2为y=0 km不同频率视电阻率和相位对应的相对误差曲线.从图中可以看出：不同频率视电阻率相对误差均比较小,最大相对误差仅为0.2%;不同频率的相位相对误差更小,最大相对误差仅为0.07%.通过对比不同频率的电阻率和相位相对误差,表明本文空间波数混合域大地电磁场三维数值模拟算法正确、精度较高,且稳定、可靠.

图2 y=0 km不同频率视电阻率和相位对应的相对误差曲线(a)ρxy；(b)ρxy；(c)φxy；(d)φyx.Fig.2 Relative error curves of apparent resistivity and phase at different frequencies

2.2 可控源电磁场计算精度

采用如图1所示的模型用于验证空间波数混合域可控源电磁场三维数值模拟算法(MSWD)的正确性和计算精度.模型参数、网格节点或单元剖分参数与上节模型参数一致,发射场源长度为5 m,场源东西端点坐标分别为(-20 m,0 m,0.1 m)和(-15 m,0 m,0.1 m)，发射电流幅值为50 A，发射频率为10 Hz.下面首先采用本文空间波数混合域可控源电磁场三维数值模拟算法(MSWD)计算了地面电磁异常场分量振幅；其次，采用传统积分方程CSEM算法(Zhdanov et al.,2006)同样计算了地面电磁异常场分量振幅，并将其作为参考场；最后，计算了二者电磁异常场分量振幅相对误差.

图3为地面z=0电磁异常场振幅及相对误差曲线.从图中可以看出：地面电磁异常场振幅响应呈“花瓣”状分布，且利用本文算法计算的电磁场与传统积分方程算法(Zhdanov et al.,2006)计算的电磁场吻合度较高，除突变介质边缘Ex分量个别点相对误差略有增大，其余测点最大相对误差均小于0.5%，由此验证了本文空间波数混合域可控源电磁场三维数值模拟算法的正确性和高精度特性.

图3 地面y=-40 m电磁异常场振幅及相对误差曲线(a)Ex;(b)Ey;(c)Hx;(d)Hy;(e)Hz.Fig.3 The amplitude and relative error curves of electromagnetic abnormal fields on the ground y=-40 m

2.3 计算效率

在验证计算精度的基础上，设计不同网格大小的模型验证空间波数混合域电磁场三维数值模拟算法(MSWD)的计算效率，并与传统有限单元法数值模拟算法计算时间进行对比，以突出本文算法在计算效率方面的优势.本文算法均采用Fortran 95语言编写，模型算例均在配置为Intel(R)Xeon(R)CPU3.1G，64GB RAM，16CPUs平台上并行计算得到，与张林成等(2017)计算三维模型算例采用的配置基本相同，便于与其对比计算效率.

参考已有文献有关计算效率的模型设计(张林成,2017)，本节设计一网格单元数为119×65×38(网格节点数为120×66×39)的模型用于测试本文基于二次场的空间波数混合域电磁场三维数值模拟算法(MSWD)的高效、低存储特性.下面首先统计了本文空间波数混合域电磁场三维数值模拟算法(MSWD)的计算时间(表1)；其次，引用了文献(张林成等,2017)四种算法的计算时间(表1)，这四种算法分别为：①基于总场有限元算法(TFE)；②基于二次场有限元算法(SFE)；③基于总场混合有限元-无限元算法(TFEIE)；④ 基于二次场混合有限元-边界元算法(SFEIE).其中，TFE/SFE算法具体是采用传统截断边界条件，近似认为边界上电场衰减为零，故设置较大的扩边计算区域.最后，对比了本文空间波数混合域电磁场三维数值模拟算法(MSWD)与传统有限元算法的计算效率.

另外，由于空间波数混合域电磁场三维数值模拟算法(MSWD)本身具有高度并行性特点，其计算时间和内存耗费并不会随着网格剖分节点数的增加呈指数增长，而是以近似线性的规律增加，这非常有利于大规模电磁数据的数值模拟，且网格剖分越多，本文空间波数混合域电磁场三维数值模拟算法(MSWD)的计算效率优势越明显.因此，设计了一个网格节点剖分为256×256×151的模型，并统计了其计算内存和计算时间(表1).

从表1可以看出：基于总场和二次场混合有限元-无限元两种算法(SFEIF，TFEIE)相对传统大区域的两种有限元算法(SFE,TFE)具有离散区域小、计算节点少、求解速度快、占用内存小等明显优势.而本文提出的空间波数混合域电磁场三维数值模拟算法(MSWD)与以上四种传统算法(SFEIF，TFEIE，SFE，TFE)相比，算法本身并行度高、正演速度比传统有限单元法快1～2个数量级、耗费内存更小.本文算法计算时间和内存耗费随着网格剖分的增加呈线性规律缓慢增加，网格剖分规模越大，该算法的计算效率优势越明显，尤其对可控源电磁法实现大规模、精细化三维数值模拟与反演成像奠定了坚实基础.

表1 五种算法计算内存和计算时间对比Table 1 The comparison of the memory and time obtained with the five algorithms

3 结论

本文提出一种具有高效、高精度特点的空间波数混合域电磁场三维数值模拟方法.该方法沿水平方向进行二维傅里叶变换，把矢量位和标量位满足的偏微分方程转化为不同波数相互独立的常微分方程，将一个超大规模问题分解为多个小问题，具有高度并行性；保留垂向为空间域，兼顾了计算精度与计算效率.该方法充分利用不同波数问题之间的高度并行性、快速傅里叶变换和追赶法求解定带宽线性方程组的高效性实现电磁场高精度三维数值模拟.设计了棱柱体模型开展数值试验，从大地电磁场和可控源电磁场的角度验证本文方法的正确性，试验结果表明本文方法正确、可靠，且精度较高.从数值求解方法的角度对比研究了本文数值方法与传统经典数值方法的计算效率，数值试验表明：在计算平台为Intel(R)Xeon(R)主频3.1 GHz，内存64 GB，16 CPUs工作站上，网格剖分规模为256×256×151的模型计算时间为45 s，占用内存为14 GB；本文方法比传统基于有限单元法的三维数值模拟方法计算效率高1～2个数量级，且网格剖分规模越大，计算效率优势越明显.

附录A

式(18)中矢量位和标量位表示为二次插值函数为

(A1)

将式(A1)代入式(18)得到以下几种形函数积分，通过查形函数积分表(徐世浙,1994)可得具体积分表达式.

第一类积分：

(A2)

第二类积分：

(A3)

第三类积分：

(A4)

第四类积分：

(A5)