基于激发极化弛豫时间谱的浸染型海底多金属硫化物岩石物性评价方法
2022-01-25伍操为邹长春吴涛周建平陶春辉
伍操为,邹长春*,吴涛,周建平,陶春辉
1 中国地质大学(北京)地球物理与信息技术学院,北京 100083 2 自然资源部第二海洋研究所,杭州 310012
0 引言
随着海洋探测技术的不断发展,开发利用海洋矿产资源已成为可能(Glasby,2002).作为海底热液活动的主要产物,海底多金属硫化物富含铜、铁、镍、金、银等金属,具有极高的开采价值,已经引起了诸多经济体以及矿业公司的注意(Glasby,2002;Hoagland et al.,2010;Hannington et al.,2011;陶春辉等,2014).海底多金属硫化物在矿床的不同层位会呈现不同的分布形态,如浸染分布型、网状分布型、块状分布型等(Komori et al.,2017).实验结果表明,海底多金属硫化物的物性尤其是激电特性与围岩存在明显不同,相比于大洋玄武岩和角砾岩,块状多金属硫化物岩石的直流电阻率要低1~3个数量级,极化率也更高(Nakayama et al.,2011;Spagnoli et al.,2016;李泽等,2019;Tao et al.,2020).海域资源调查的结果同样表明,硫化物矿床会出现明显的极化率异常(Goto et al.,2008,2011;Kowalczyk,2011;Ishizu et al.,2019).为了对海底多金属硫化物进行勘探开发,钻探和取心是必不可少的,在海底钻孔中开展激发极化测井,能够对各层位的激电特性进行评价,进而为含矿层的识别和评价工作提供有力支撑.
激发极化法(IP)是基于岩石对电荷可逆储存性的一种方法,广泛应用于陆域金属矿勘探、油气勘探、水文地质勘查等工作中,可以分为频率域和时间域两大类(Kemna et al.,2012).频率域激发极化法(FDIP)近年来以复电阻率法(SIP)为主,即在一个较大的频率范围(通常为10-3~103Hz)内开展连续扫频测量,通过记录到的复电阻率谱和相位谱来分析岩石的激电特性.时域激发极化法(TDIP)通过对地层通入一段时间的恒定电流,记录断电后的二次电压衰减曲线,并基于该衰减曲线对地层的激电特性进行分析(Florsch et al.,2011;Dusabemariya et al,2020).因为SIP具有较大的扫频测量区间,一般被认为能够比TDIP更加精细地对岩石激电特性进行评价,但其单次测量时间较长,且对仪器性能要求高,需要能够连续发射多种频率的电流.TDIP只需要发射单一频率的电流,对仪器性能要求低,一般直流电阻率仪器都能完成测量,且单次测量时间短,因此能够更加经济、高效地在海底钻孔中部署.
在金属矿勘探领域,目前对TDIP资料的分析方法主要有两种,第一种是直接对岩石的视直流电阻率和视极化率进行分析(Yoshikawa H and Yoshikawa M,1978;Bartetzko et al.,2003;李兆祥等,2015;李建良,2016;张刚和吕庆田,2019).网状、块状分布型海底多金属硫化物岩石具有明显的低电阻率和高极化率特征,较易识别.就多金属硫化物呈浸染状分布的岩石而言,金属硫化物颗粒之间的连通性较差,且小粒径硫化物颗粒具有较高的截止频率,在低频电场中易表现出绝缘特性,此时岩石的导电作用由孔隙中的海水主导,因此含矿岩石与同等孔隙度的未矿化岩石在直流电阻率上可能差异不大(Revil et al.,2015;Komori et al.,2017).可见,直流电阻率在浸染型海底多金属硫化物矿层的识别和评价上可能具有一定的局限性.极化率受围岩骨架导电性的影响较小,但其作为一个单一的数值,能够反映的地层信息较少.第二种分析方法是基于时域Cole-Cole模型,利用反演算法计算出TDIP二次衰减曲线(即视极化率曲线)的弛豫时间常数τ、金属因子等频谱激电参数来分析地层的激电特性.目前第二种方式的应用较少,一些反演算法的效率和精度仍需进一步提高(蓝常斌等,2012;曹平华和罗润林,2014;杨红等,2015;彭伟等,2018).在石油测井领域,根据电化学作用下的载流子运移特征,可以基于砂、泥岩的TDIP二次衰减曲线计算弛豫时间谱.弛豫时间谱一般用于评估储层的孔径分布以及渗透率、孔隙度等参数,通过与其他测井方法结合,还可以用于评估储层的阳离子吸附能力、剩余油饱和度等参数(童茂松等,2005;Tong et al.,2006;Liu et al.,2014a).近年来,弛豫时间谱的反演算法取得了较大的发展,精度和速度都不断提高(Liu et al.,2014b;童茂松,2015;Zhang et al.,2016).
尽管弛豫时间谱方法在石油测井领域取得了长足的发展,但在金属矿勘探尤其是海底多金属硫化物勘探评价中的应用较少.本研究基于金属硫化物的激发极化机理和模型,改进了弛豫时间谱反演方法,并对数值模拟数据和实验测量数据开展弛豫时间谱分析,研究弛豫时间谱和浸染型海底多金属硫化物岩石激电特性参数之间的关系.
1 弛豫时间谱分析方法
本节首先从金属硫化物的激发极化理论出发,结合电子导体的激发极化衰减模型,提出适用于金属硫化物岩石的弛豫时间谱反演方法,随后基于该方法对理论以及实测TDIP数据进行处理与分析,同时还计算出时间域Cole-Cole模型参数进行对比.
1.1 弛豫时间谱反演的基本理论
原位环境下海底多金属硫化物岩石的孔隙中充满了海水,因此金属硫化物颗粒可视为处于溶液之中.纯净的金属硫化物为本征半导体,在岩石两端施加恒定电场,金属硫化物颗粒内部带负电荷的电子和带正电荷的电子空穴(假想)会分别向颗粒两端移动,持续供电一段时间后,正负电荷会分别聚集到颗粒两端,此时硫化物颗粒可视为一个电偶极子.撤去外电场后,颗粒两端的电荷逐渐重新回到平衡位置,从而产生扩散电场,即TDIP测量的二次电压(图1).岩石孔隙也会产生激发极化效应,但远弱于金属硫化物颗粒.岩石整体的激发极化效应是其内部各种极化源的激发极化效应的线性叠加,对于砂、泥岩而言,岩石内部的极化源为一系列不同直径的孔隙,而浸染型海底多金属硫化物岩石内部的极化源除孔隙外还包含各种金属硫化物颗粒.
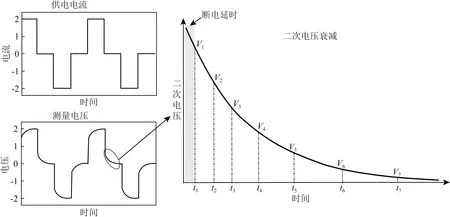
图1 时域激发极化法测量示意图Fig.1 Schematic diagram of time domain induced polarization measurement

(1)
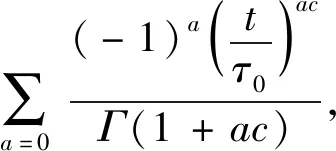
(2)
从式(2)中求解出G(τ)就能够获得含矿岩石的弛豫时间谱,进一步建立弛豫时间谱与岩石激电参数的对应关系,可以更加全面地对岩石的物性进行分析.
为了求取G(τ),需要将式(2)离散化,并构建线性方程组
Ax=b,A∈Rn×m,x∈Rm,b∈Rn,
(3)
其中bn×1为二次衰减曲线的测量点,即bn×1=(V1,V2,…,Vn)T;xm×1为计算得到的G(τ),即xm×1=(G1,G2,…,Gm)T.An×m为预先设置好的离散化单元矩阵,
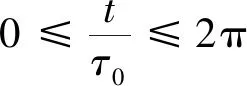
(4)
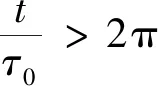
(5)
为了降低测量数据信噪比对xm×1的影响,需要对上述方程式进行正则化处理,即在方程式后加入一个约束项,约束项包括正则化因子λ和约束矩阵W(童茂松,2015).新的方程组可以写为
min∶‖b-Ax‖2+λ2‖Wx‖2.
(6)
1.2 TDIP数据的获取和弛豫时间谱反演
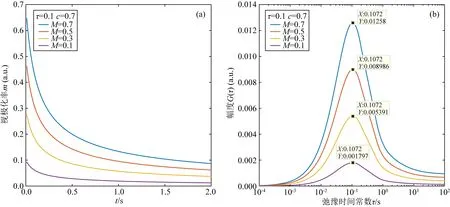
为了研究弛豫时间谱与海底多金属硫化物岩石激电特性参数间的关系,本研究分别对理论数据和实测数据进行弛豫时间谱分析.理论数据是基于时间域Cole-Cole模型(式(1))生成的二次衰减曲线.Cole-Cole总极化率和弛豫时间常数是矿体勘探评价中最关心的参数,因此生成两类二次衰减曲线,第一类曲线的总极化率M相同,弛豫时间常数τ不同;第二类曲线的弛豫时间常数τ相同,总极化率M不同.
实测数据是在实验室模拟海底环境,并对人工岩样进行时域激发极化测量所得到的数据.人工岩样为玄武岩粉末和硫铁矿颗粒混合并水泥胶结制成的直径25 mm标准柱状样,可分为两类,第一类岩样具有相同的金属硫化物体积分数,不同的金属硫化物粒径,第二类岩样具有相同的金属硫化物粒径,不同的金属硫化物体积分数.岩样的孔隙度均介于0.25~0.29之间,其基本信息如表1所示.采用矿化度与海水相当的NaCl溶液(3.5%)对上述岩样进行饱和,该溶液在18 ℃时的电导率为3.8 S·m-1.基于四电极法开展测量,夹持装置总体上分为电极盒、岩样套筒两个部分.电极盒由有机玻璃制成,其中充满了NaCl溶液(与岩样饱和液相同).供电电极为一对8 cm×8 cm网状电极,固定在电极盒的内边缘,测量电极为一对Ag-AgCl不极化电极(图2).测量前,首先将岩样置于100 ℃烘干箱中干燥12 h,随后把岩样放入真空加压饱水仪器中,设定压力为30 MPa,饱水24 h.测量时,岩样被放置于夹持装置中央的绝缘胶套中,并被软管夹夹紧,仅露出两个端面,该处理能够保证测量时孔隙水不易挥发,同时避免岩样表面形成旁路电流.测量仪器为加拿大GDD公司生产的SCIP岩心电性测量仪,设置供电时间为4 s,供电电压为3 V,采样数为20,采样区间为断电后20~2890 ms(与理论数据不同,实测数据的视极化率单位为mV/V).
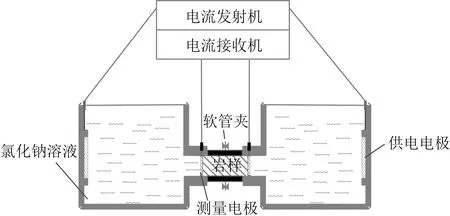
图2 本研究中采用实验装置的示意图Fig.2 Schematics of the experimental apparatus used in this study
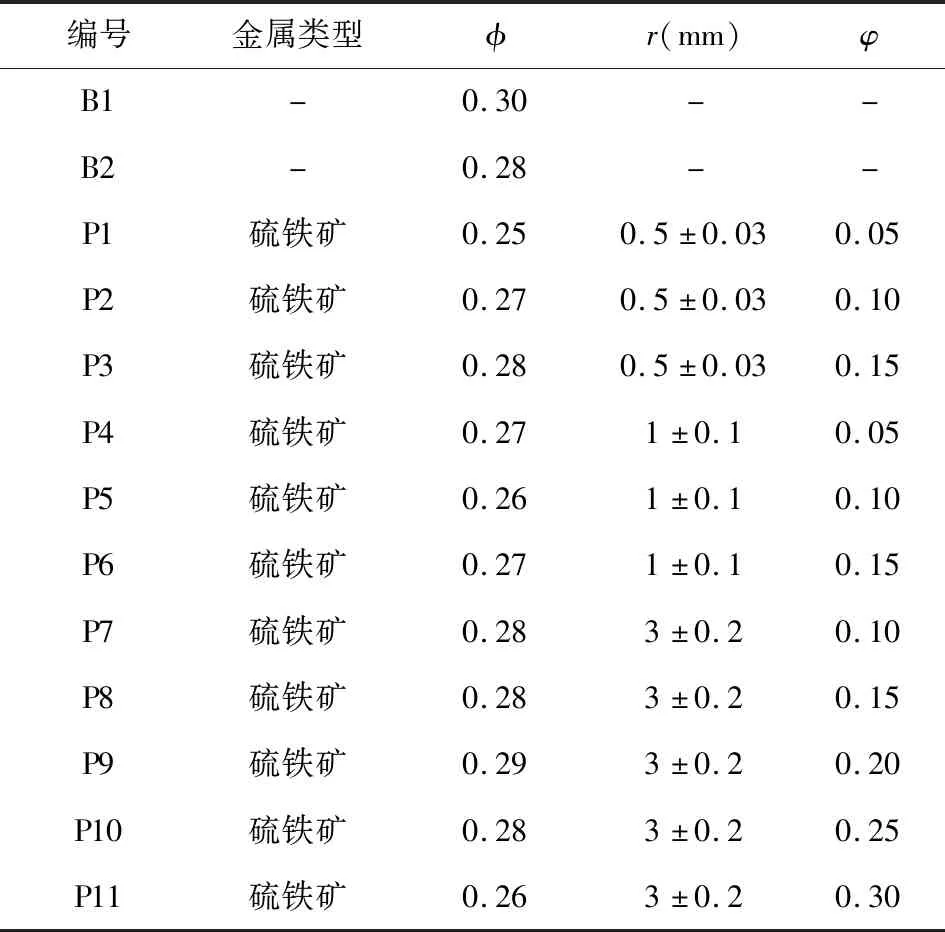
表1 实测岩样的特征.φ表示岩样的孔隙度,φ表示金属硫化物的体积分数,r表示金属硫化物颗粒的平均粒径
本研究中弛豫时间谱的求解过程可以分为以下步骤:(1)在一定范围内(0.001~10 s)随机选择一系列τ,从而设定式(3)中的离散单元矩阵An×m;(2)从测量得到的视极化率衰减曲线中选择一定的数据点(t,m);(3)构建线性方程组Ax=b;(4)对方程组进行正则化处理,加入正则化因子和约束矩阵,其中正则化因子通过“L”曲线法选取,约束矩阵采用单位矩阵;(5)采用吉洪诺夫正则化方法求解方程,获得初始弛豫时间谱,即(τ,G(τ)).获得的G(τ)可能会出现负值,需要对计算结果进行非负约束.非负约束分为以下步骤:1)将G(τ)的计算值代入式(6),计算m′=Ax,以及实际值与理论值的差Δm=m-m′;2)将Δm代入式(6),计算出校正值ΔG(τ),并令G(τ)k=G(τ)+ΔG(τ);3)如果G(τ)k中的每个值都非负,则将G(τ)k作为最终解,否则重复上述过程.
1.3 TDIP数据的Cole-Cole模型参数反演
为了对比Cole-Cole模型和弛豫时间谱对多金属硫化物岩石物性特征的评价效果,除了计算弛豫时间谱外,还对部分实测数据的Cole-Cole模型参数进行了求取.基于时域Cole-Cole模型(式(1)),采用模拟退火法对二次衰减曲线进行拟合,最小化目标函数可以写为
(7)
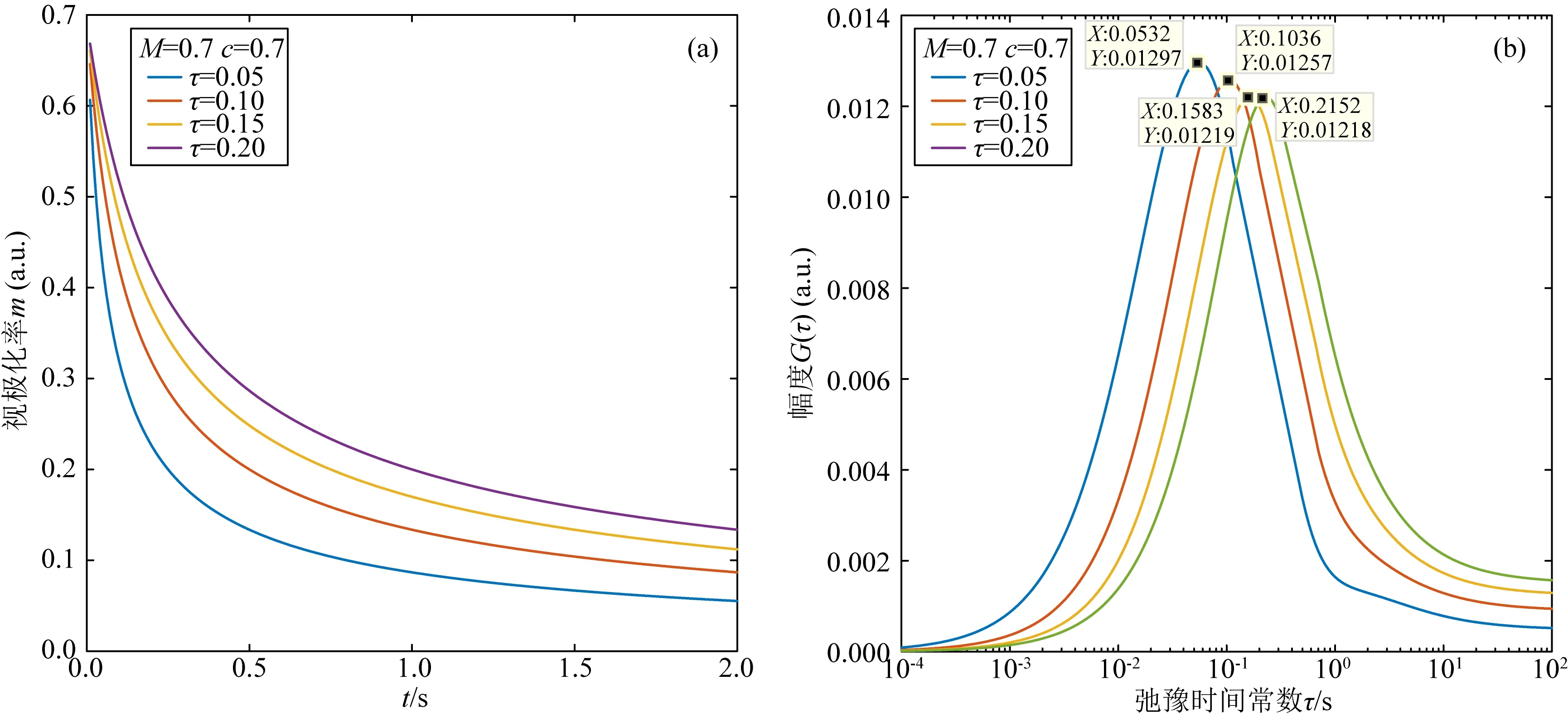
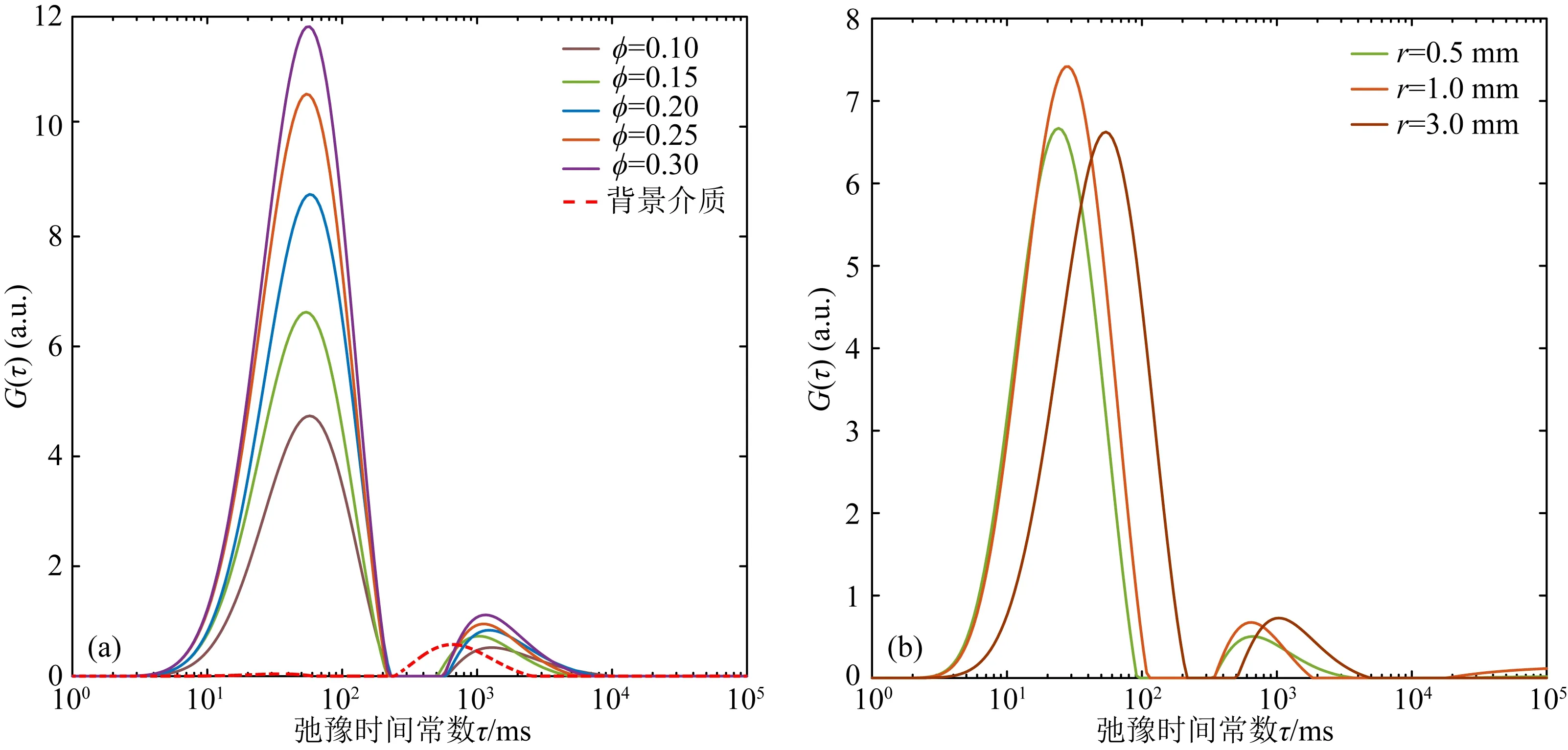
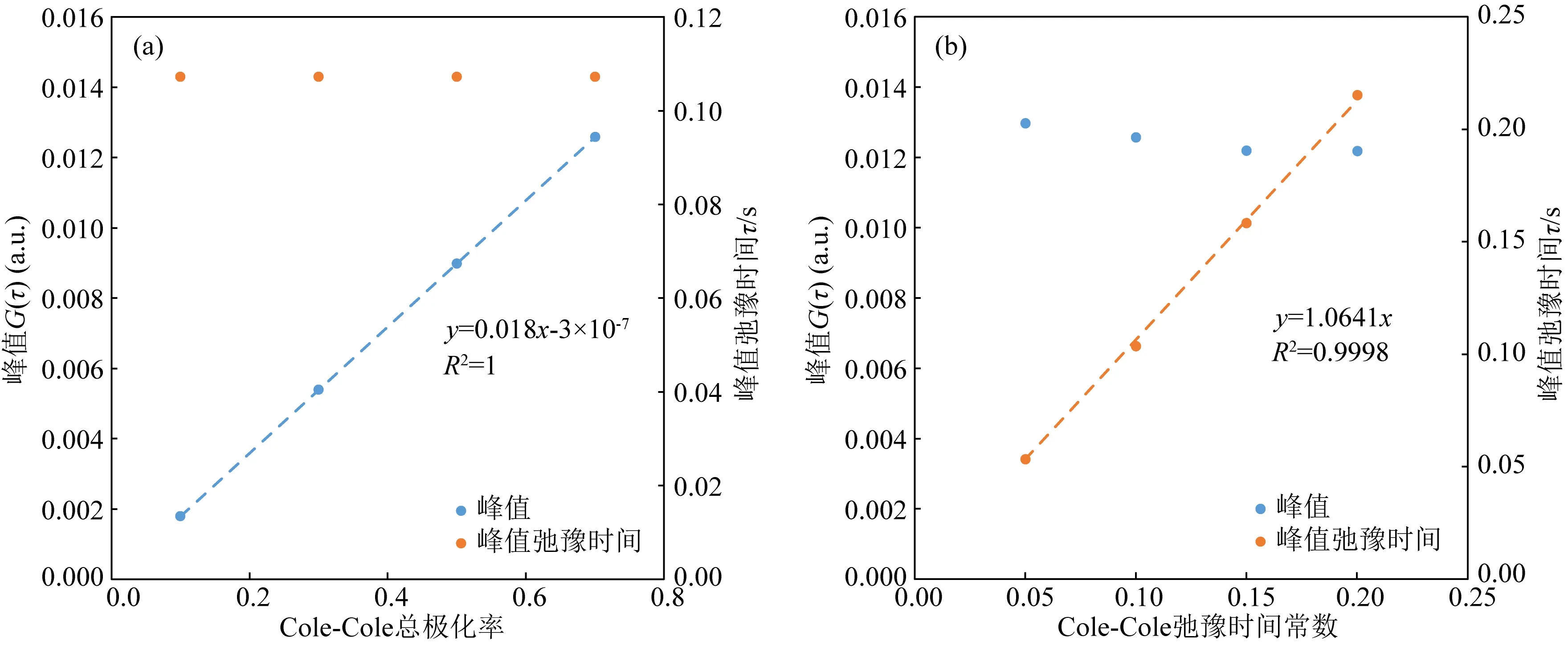
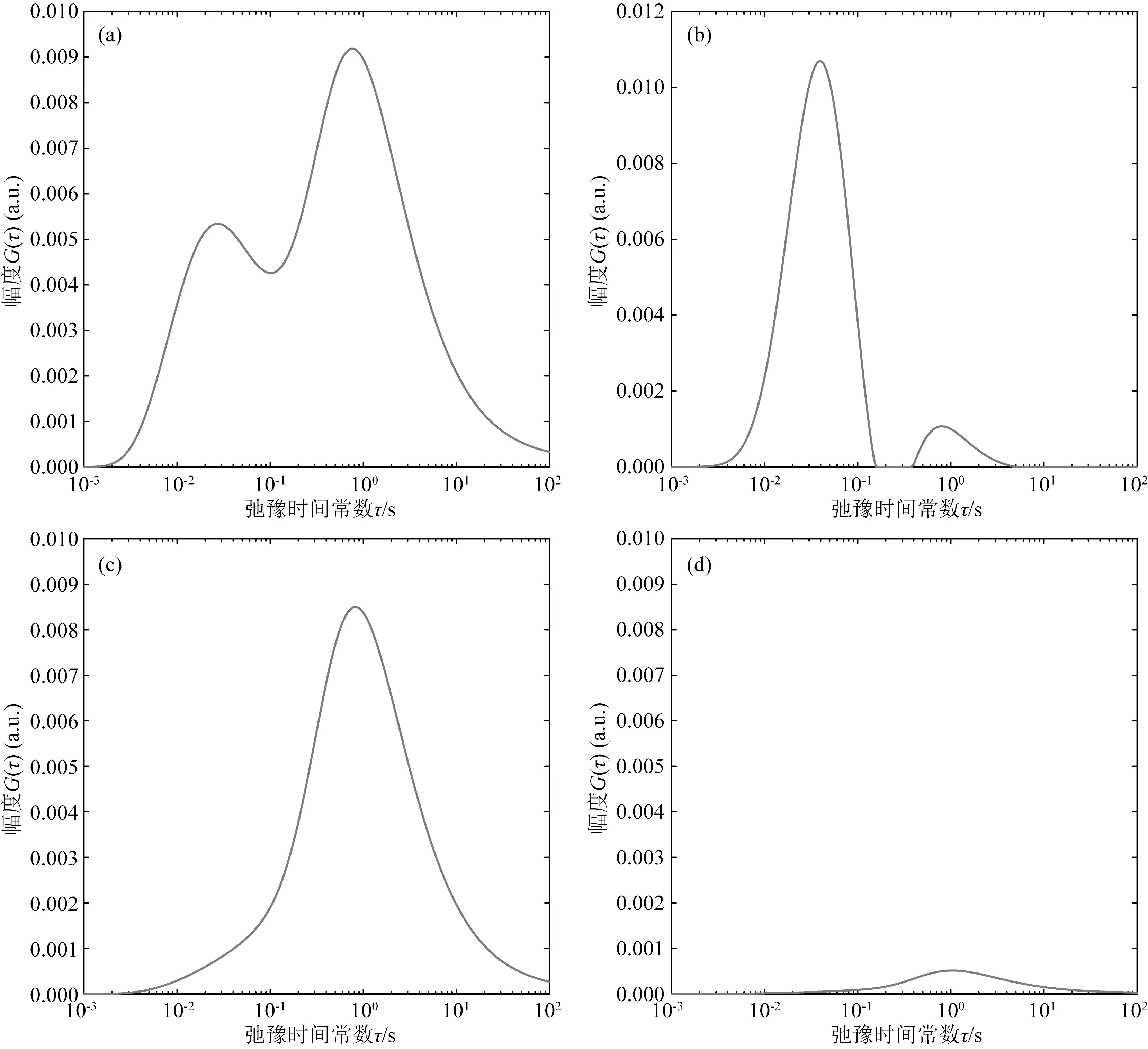
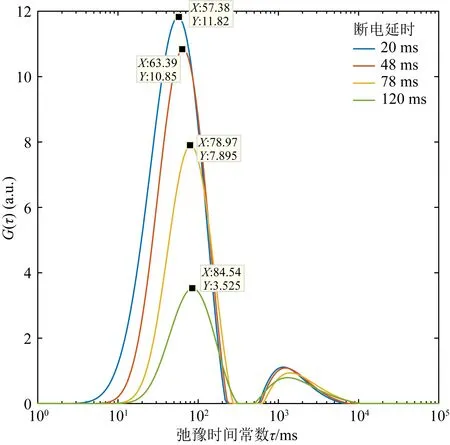
其中mobs(ti)为ti时刻实测的视极化率,mfit(ti)表示拟合的ti时刻的视极化率,N表示数据点的个数.采用数据本身来约束总极化率的大小,即mobs(t1) 利用推导出的基于本征半导体激发极化模型的反演方法以及模拟退火法分别计算出了理论和岩石物理实验数据的弛豫时间谱及总极化率、弛豫时间常数等Cole-Cole模型参数. Cole-Cole模型与理论数据的拟合效果较好,相对误差较低,体现了反演算法的可靠性(图3a).Cole-Cole模型与实测数据在衰减早期拟合效果相对较好,但在衰减后期拟合效果略差(图3b). 图3 理论二次衰减曲线(a)和岩样P7实测二次衰减曲线(b)的Cole-Cole模型拟合结果Fig.3 Cole-Cole model fitting of the synthetic secondary decay curve (a)and laboratory measured secondary decay curve of sample P7 (b) 对于实测数据而言,保持金属硫化物粒径不变,当金属硫化物的体积分数从0.10增加至0.30时,总极化率从0.31线性增加至0.95.此外,对比不同金属硫化物粒径岩样的总极化率可以发现,该线性关系的斜率受金属硫化物粒径变化的影响较小(图4).实测岩样的二次电压早期衰减较快,拟合曲线与实测曲线一些微小的差异就会导致求出的Cole-Cole弛豫时间常数出现较大变动,这导致不同实测二次衰减曲线的Cole-Cole弛豫时间常数差异较大. 图4 Cole-Cole总极化率与硫铁矿体积分数的关系Fig.4 Cole-Cole total chargeability versus the volume content of pyrite 理论数据的弛豫时间谱均为单峰形态(图5,图6).保持弛豫时间常数τ和Cole-Cole系数c不变,当总极化率M从0.1增加至0.7时,弛豫时间谱的峰值从0.0017上升至了0.012,但峰值弛豫时间始终不变.保持总极化率M和Cole-Cole系数c不变,当弛豫时间常数τ从0.05 s上升至0.20 s时,弛豫时间谱的峰逐渐右移,峰值稍有降低,但降低的趋势越来越不明显. 图5 相同τ和c,不同总极化率M的理论衰减曲线和弛豫时间谱Fig.5 The synthetic decay curve and its relaxation time spectrum with different total chargeability M under the same τ and c 图6 相同M和c,不同弛豫时间常数τ的理论衰减曲线和弛豫时间谱Fig.6 The synthetic decay curve and its relaxation time spectrum with different relaxation time constant τ under the same M and c 与理论数据的弛豫时间谱不同,实测数据的弛豫时间谱均为双峰型,左峰位于20~70 ms,右峰位于600~1000 ms(图7).含矿岩石左峰的峰值介于4.73~11.83之间,而右峰的峰值几乎都小于1.不含硫化物颗粒的纯玄武岩岩样的右峰峰值以及峰值弛豫时间均与含矿岩样接近,但左峰的峰值远远小于含矿岩样.对于硫铁矿体积分数不同、粒径相同的岩样,当硫铁矿的体积分数从0.05增加至0.3时,左峰峰值从4.73上升至11.83,但峰值弛豫时间不发生变化.对于硫铁矿粒径不同、体积分数相同的岩样,当硫铁矿粒径从0.5 mm增加至3.0 mm时,弛豫时间谱的左峰从24.77 ms移动到了57.38 ms,峰值变化相对较小. 图7 实验岩样的弛豫时间谱.(a)相同硫铁矿粒径,不同硫铁矿体积分数的岩样;(b)相同硫铁矿体积分数,不同硫铁矿粒径的岩样Fig.7 Relaxation time spectrum of measured samples with (a)various volume content and same grain radius or (b)various grain radius and same volume content of pyrite 理论数据弛豫时间谱的峰值弛豫时间与Cole-Cole弛豫时间常数几乎是相等的,峰值则与Cole-Cole总极化率M呈线性正相关关系(图8).Cole-Cole弛豫时间常数的改变对弛豫时间谱峰值的影响很小,总极化率的改变则对峰值弛豫时间的影响很小.可见,基于时域激电数据的弛豫时间谱可以直接获取其Cole-Cole模型参数. 图8 理论衰减曲线弛豫时间谱左峰峰值和峰值弛豫时间与总极化率(a)及弛豫时间常数(b)关系Fig.8 Amplitude and peak relaxation time of the left peak of the relaxation time spectrum versus (a)the total chargeability and (b)relaxation time constant of the synthetic decay curves 对于不含金属硫化物颗粒的纯玄武岩岩样B1,其激发极化效应完全由孔隙产生.一般来说,大孔隙的弛豫时间常数较大,小孔隙的弛豫时间常数较小(童茂松等,2006).本研究所采用的人工岩样孔隙较为发育,以大孔为主,小孔较少.岩样B1的弛豫时间谱表现为左峰较小,右峰相对较大,与岩样的孔隙结构特征相符(图7红色虚线所示).此外,含矿岩样与纯玄武岩岩样的右峰具有相近的峰值以及峰值弛豫时间,且含矿岩样右峰的形态并没有随金属硫化物体积分数、粒径的变化而发生改变.因此,含矿岩样弛豫时间谱的两个峰对应了岩石中的两类极化源,短弛豫时间,大峰值主要代表金属硫化物颗粒的激发极化作用;长弛豫时间,小峰值主要代表了玄武岩的激发极化作用.每块岩样弛豫时间谱右峰的峰值以及峰值弛豫时间均不相同,这也反映了岩样孔隙结构的复杂性.从弛豫时间谱的整体形态上看,含矿岩石的激发极化效应由金属矿物主导,孔隙结构上的差异对岩石整体激发极化效应的影响较小.根据电子导体的激发极化理论,浸染型金属硫化物的激发极化强度只与其体积分数有关,而弛豫时间常数只与其粒径以及颗粒内部载流子的扩散系数有关(Revil et al.,2015).本研究中实测数据的弛豫时间谱计算结果与上述理论吻合较好,随着金属硫化物体积分数的增大,含矿岩石弛豫时间谱左峰峰值呈上升趋势,而峰值弛豫时间不受影响,随着金属硫化物粒度的增大,左峰逐渐右移,而峰值受影响较小.本研究中的岩样只含有一种金属硫化物,即硫铁矿,而天然海底多金属硫化物岩石中可能还会含有黄铜矿、方铅矿等金属硫化物.这些金属硫化物的激发极化机理相同,激发极化效应均来自于内部载流子的迁移,相关实验研究也表明这些硫化物具有相近的扩散系数(Revil et al.,2015).因此,前述研究结果可以从硫铁矿推广至其他金属硫化物.从实测数据的分析结果来看,弛豫时间谱不仅能够对岩石中不同类型的极化源进行区分,还可以对浸染型金属硫化物的含量和粒度进行评估. 时间域Cole-Cole模型只包含一个弛豫时间常数τ,所以理论数据的弛豫时间谱也为单峰型,而实测数据的激发极化信号由硫铁矿颗粒和玄武岩的激发极化信号叠加而成.在海底这种高矿化度环境下,硫铁矿颗粒极化信号强,衰减速度快,在实测衰减曲线的早期起主导作用,玄武岩极化信号弱,但衰减速度慢,在实测衰减曲线的后期起主导作用,故含矿岩样弛豫时间谱为双峰型.只含有一个弛豫时间常数τ的时间域Cole-Cole模型始终是在对岩石整体的激发极化效应进行描述,在对同时含有多个极化源的极化信号进行分析时具有局限性,因此时间域Cole-Cole模型对理论数据的拟合效果要好于实测数据(图3). 弛豫时间谱可以对岩石整体的激发极化效应进行分解,对具有不同弛豫时间常数的极化源分别进行描述,从而弥补时间域Cole-Cole模型的不足.天然海底多金属硫化物岩石内部均包含有多个极化源,例如多种不同粒径的硫化物颗粒共存,或者浸染状分布的硫化物与网脉状、块状分布的硫化物共存等.不同类型的极化源,在弛豫时间谱上表现为不同形态的峰,例如,玄武岩等背景介质的激发极化效应表现为大弛豫时间,小峰值;浸染型多金属硫化物的激发极化效应表现为小弛豫时间,大峰值;可以推测块状、网状分布的多金属硫化物的激发极化效应表现为大弛豫时间,大峰值,因为此时硫化物在岩石内部形成了导电网络,增大了弛豫时间.当岩石中同时存在多种极化源时,可以推测其弛豫时间谱将呈现出多种形态,例如(1)双峰型a(图9a),此时岩石中既有网脉状、块状分布的硫化物,又有浸染状分布的硫化物;(2)双峰型b(图9b),此时岩石中仅含有浸染状分布的硫化物;(3)单峰型a(图9c),岩石中主要为网脉状或块状分布的硫化物;(4)单峰型b(图9d),岩石几乎不含硫化物. 图9 不同极化源叠加形成的弛豫时间谱Fig.9 Relaxation time spectrum generated by superposition of various polarization sources 在多金属硫化物矿的评价工作中,常通过复电阻率测量来获得岩石的频谱和相位谱,并基于频率域Cole-Cole模型计算出总极化率、弛豫时间常数等参数,以此来分析多金属硫化物的品位和分布特征.时域激发极化测井频率单一,通常被认为反映的地质信息少于复电阻率测井,然而相比于复电阻率测井,时域激发极化测井更适合在海底钻孔中开展.通过对时域激电数据求取弛豫时间谱,同时结合Cole-Cole模型参数,尤其是总极化率进行分析,可以更加充分地利用时域激电资料,使时间域激电测井达到接近复电阻率测井的效果,有利于海底多金属硫化物勘探工作的进行. 进行时间域激发极化测量时,为了降低电磁耦合效应的影响,通常在断电后经过一段延时才开始采集二次衰减信号,陆域金属矿勘探中的断电延时可达数百毫秒.金属硫化物的激发极化弛豫时间常数与地层水矿化度呈反比关系(Revil et al.,2018).由于陆域环境中地层水矿化度通常较低,金属硫化物颗粒的二次电位衰减较慢,断电延时对测量结果的影响较小.海水的矿化度远高于陆域环境中的地下水,金属硫化物在海底环境下的弛豫时间常数可能远小于在陆域环境中,因此二次电位的衰减速度也远快于在陆域环境中,若选择较长的断电延时,记录到的衰减曲线很可能是不完整的. 为了研究断电延时对弛豫时间谱反演结果的影响,将岩样P11的二次衰减曲线用不同的断电延时截断,并反演出弛豫时间谱(图10).当断电延时从20 ms增加至120 ms时,弛豫时间谱的左峰峰值从11.82下降至了3.52,同时峰值弛豫时间从57.38 ms上升至了84.54 ms,右峰受断电延时的影响较小.可见,海底环境下断电延时对弛豫时间谱反演结果的影响是较大的,尤其对短弛豫时间的极化源的影响较大.较长的断电延时会使记录到的二次电压缺失早期快速衰减的部分,造成短弛豫时间极化源的激发极化强度被低估,弛豫时间常数被高估,进而导致浸染型金属硫化物的体积分数被低估,粒度被高估.从本研究的结果来看,在高矿化度环境下对浸染型多金属硫化物岩石开展时域激发极化测量时,断电延时应小于20 ms,最好采用全波形记录,即同时连续对一次场和二次场电位差进行采集. 图10 不同断电延时下含矿岩石P11的弛豫时间谱Fig.10 Relaxation time spectrum of sample P11 with different delay time after current off (1)本文提出的方法能够有效对浸染型金属硫化物岩石的激发极化特性进行评价.弛豫时间谱不仅实现了对岩石极化率、弛豫时间常数等物性的评价,还能够区分岩石中的不同极化源.此外,金属硫化物的体积分数与弛豫时间谱的峰值呈线性正相关,其粒度则可以通过峰值弛豫时间常数确定. (2)根据不同极化源的激发极化特性,将海底多金属硫化物岩石的弛豫时间谱划分为四种典型类型.四种类型能够反映浸染分布型金属硫化物、块状/网状分布型金属硫化物以及围岩等不同极化源共存时岩石的激发极化特性. (3)时间域激发极化测量的断电延时是影响浸染型海底多金属硫化物岩石激发极化特性评价的重要因素.较大的断电延时会导致弛豫时间谱的峰值被低估,峰值弛豫时间被高估,进而导致金属硫化物的体积分数被低估,粒度被高估.2 结果
2.1 Cole-Cole模型参数
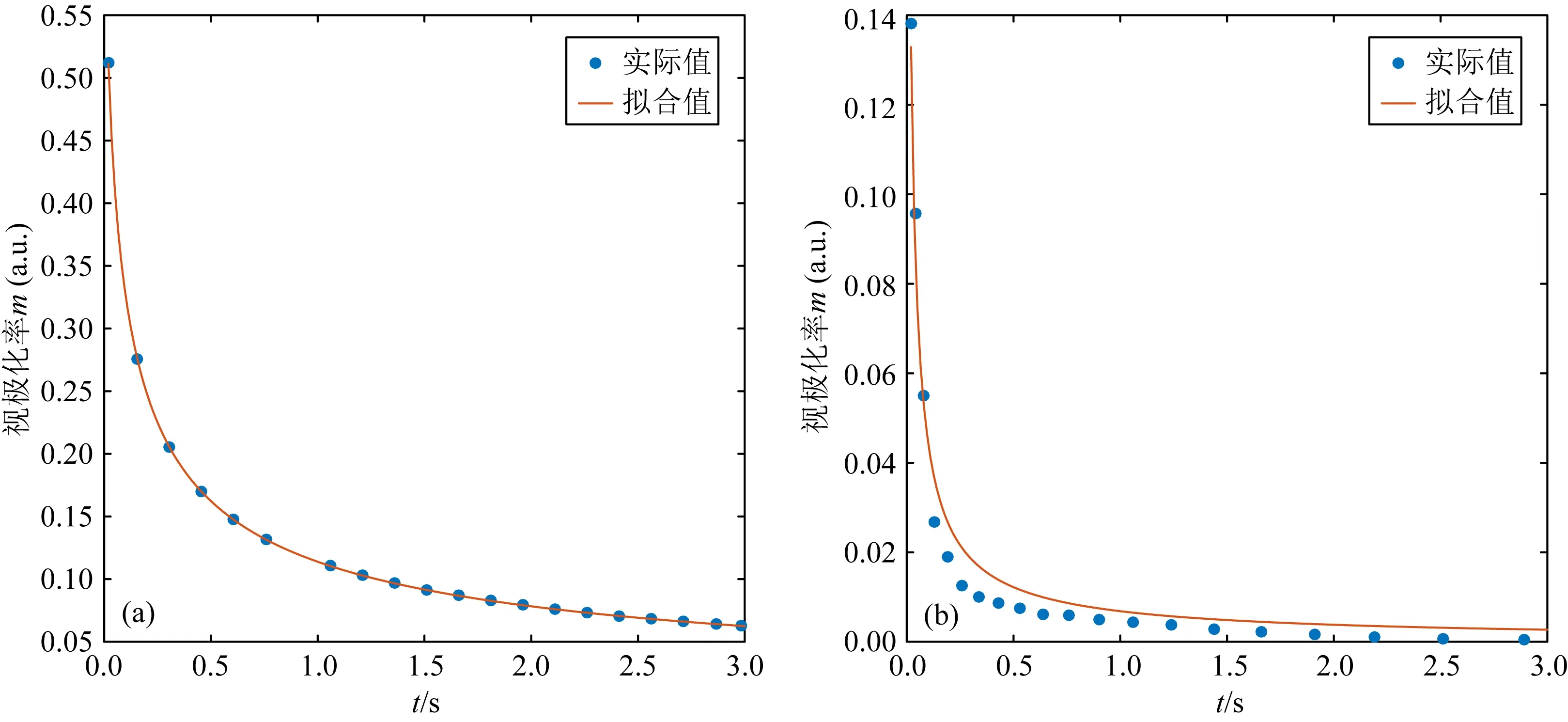
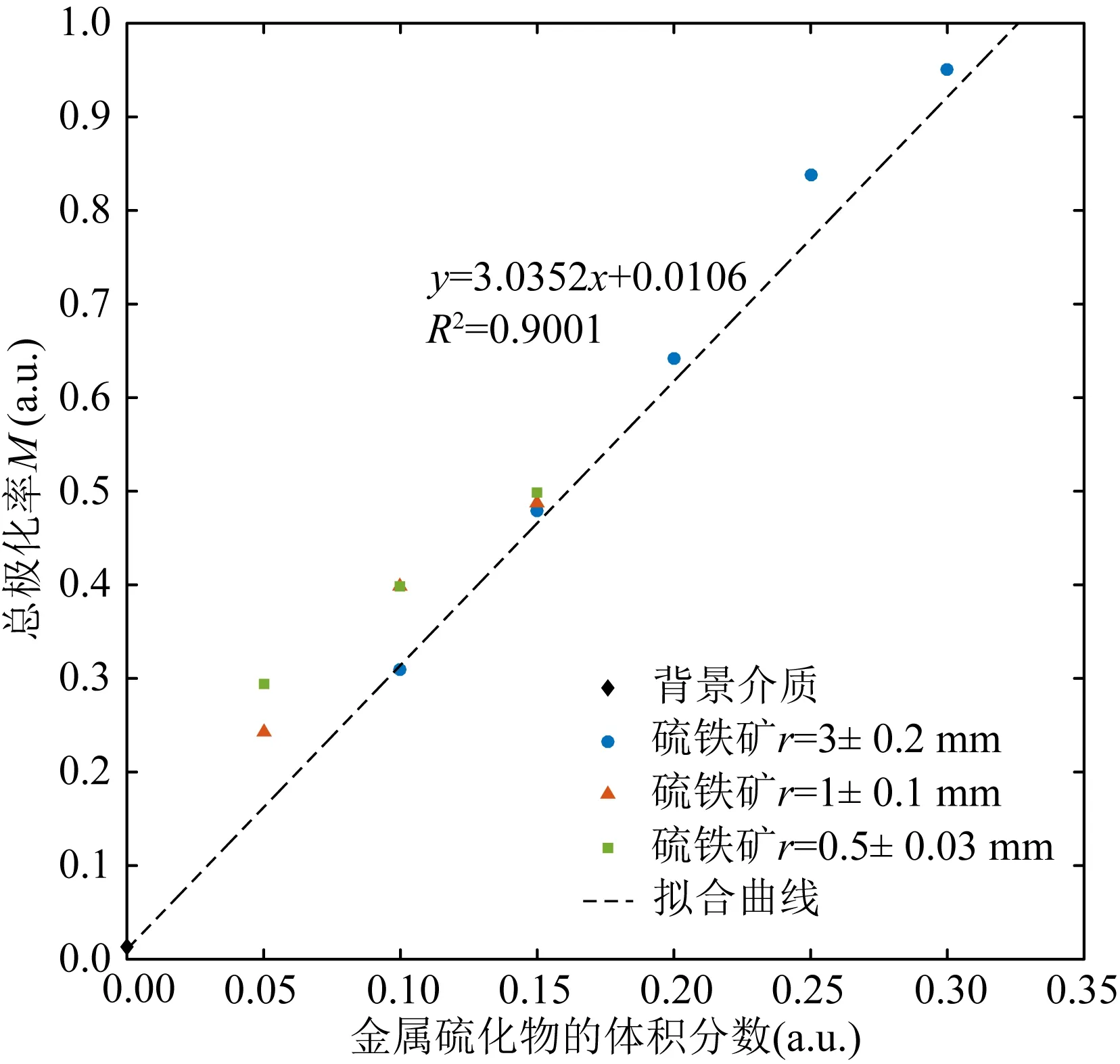
2.2 弛豫时间谱
3 讨论
3.1 理论数据和实测数据的弛豫时间谱分析
3.2 时域Cole-Cole模型与弛豫时间谱对比
3.3 断电延时对弛豫时间谱的影响
4 结论
