黏弹性VTI介质微地震正演模拟与震源机制全波形反演

唐杰，刘英昌，韩盛元，孙成禹

中国石油大学(华东)地球科学与技术学院，青岛 266580

0 引言

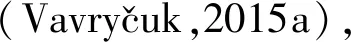
波形反演是一种数据驱动的高分辨率模型参数估计方法，其强大之处在于它能够利用记录的相位和振幅信息，通过伴随状态法获得目标函数的梯度(Fichtner et al.，2006；刘立斌等，2020)，进而通过优化算法获得目标模型参数.Tarantola(1984)指出数据残差在时间上的反向传播波场与正向传播波场的互相关有助于迭代地生成高分辨率的速度模型.结合伴随状态法，波形反演技术只需两次模拟就可以估计不同类型参数(不仅仅是速度参数)的梯度.虽然波形反演主要用于速度模型构建(孙史磊等，2020)，但微地震波形中包含的信息也可以用于反演震源参数等信息(Virieux and Operto，2009).针对各向异性介质条件下的震源参数反演，Michel和Tsvankin(2014)对弹性VTI介质中微震事件的震源位置和矩张量进行波形反演梯度计算.Grechka(2015)分析了单井微震资料全矩张量反演的可行性，认为在VTI介质中的垂直井中由于方位各向异性导致慢度矢量偏离包含射线轨迹的平面，通过处理能够得到理论上唯一的地震矩张量.Michel和Tsvankin(2019)的研究表明三维各向异性波形反演可以为微地震勘探提供高分辨率的速度模型和改进的定位结果，联合矩张量反演能够取得较好的效果.Li 等(2021)提出了一种考虑VTI介质中速度各向异性的微震震源机制反演方法，通过对合成波形和观测波形的匹配，仅用P波进行地震矩张量反演提高鲁棒性，研究表明各向异性参数的偏差会引起非DC成分的反演误差.这些研究针对的是弹性各向异性介质中的波形反演，地层的各向异性吸收衰减作用对震源机制反演的影响并没有得到充分的研究，地层的吸收衰减会影响微震信号的波形、频谱和信噪比等，从而降低震源机制的反演精度，矩张量反演结果误差会导致不同属性参数解释结果出现不同程度的偏差，因此需要对黏弹性各向异性介质中的震源机制反演开展进一步研究.

本文研究了各向异性黏弹性VTI介质中的微地震震源机制反演方法，首先基于分数阶拉普拉斯算子解耦的波动方程实现了黏弹性VTI介质矩张量震源的正演模拟，分析了衰减各向异性与震源机制对波场的影响；然后利用伴随态法计算了非均匀VTI介质中的矩张量源的目标函数梯度，采用梯度下降算法更新了震源参数，获得了震源机制矩张量反演结果，并通过实验测试验证了该方法的有效性.

1 原理

1.1 各向异性衰减VTI介质中微地震波场模拟

微地震的震源机制可以采用矩张量M的形式表示(Jost and Herrmann，1989)：

(1)

pM=pISO+pCLVD+pDC,

(2)

各成分的矩张量分量如表1所示，ISO成分由归一化单位矩阵表示；CLVD成分(Lay and Wallace，1995)被用于近似水力压裂过程中发生的拉伸事件，与拉伸裂纹不同的是，CLVD源不涉及任何体积变化，因为沿一个轴的应变会通过沿其他轴的收缩或膨胀进行补偿(Knopoff and Randall，1970).

表1 本文采用的震源机制及其分量Table 1 Focal mechanisms and components used in this paper

VTI介质是具有垂向对称轴的横观各向同性介质，其弹性系数矩阵可由C11、C13、C33、C55与C66表示.衰减各向异性也会影响地震波的振幅与相位的变化规律，通过品质因子矩阵能够表征各向异性衰减，矩阵元素可以通过复刚度系数的实部与虚部的比值来确定.黏弹性VTI介质的Q矩阵满足：

(3)

黏弹性各向异性介质中的应力-应变关系可以表示为：

σ(x,t)=ψ(x,t)*∂tε(x,t),

(4)

式中σ=(σxx,σyy,σzz,σyz,σxz,σxy)T表示应力张量，ε=(εxx,εyy,εzz,εyz,εxz,εxy)T表示应变张量，x表示空间位置矢量，ψ表示松弛函数矩阵，矩阵中的每个分量可以表示为：

(5)

式中Γ表示伽马(Gamma)函数，t0表示参考频率ω0对应的参考时间，γij=arctan(1/Qij)/π表示与Qij相关的无量纲参数，H(t)表示阶跃函数.

将各元素分量代入式(4)可以得到：

(6)

(7)

参考Caputo和Mainardi(1971)对分数阶导数的定义，黏弹性介质应力-应变关系可以表示为：

(8)

其中，δ是克罗内克函数.将VTI介质弹性系数矩阵代入式(8)可以获得时间分数阶形式：

(9)

时间分数阶导数的求解需要大量内存与计算时间，而通过近似可以将其转化为由分数阶拉普拉斯算子表征的空间分数阶导数，同时波场也可以解耦为衰减项与频散项，提高计算效率并有利于后续工作开展.在弱衰减的假设下，时间分数阶导数可以由分数阶拉普拉斯算子代替(Zhu and Harris，2014)，即：

(10)

则：

(11)

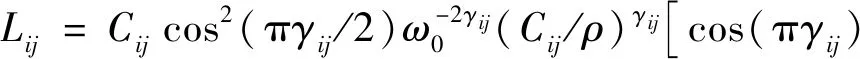
结合动量守恒公式与应变-位移关系可得到黏弹性VTI介质分数阶拉普拉斯算子波动方程的速度-应力形式：

(12)

(12′)

通常正应力和剪应力是直接施加在相应的网格点上，而在交错网格离散的伪谱法中正应力和剪应力不是在同一位置计算的.假设矩张量源作用于正应力分量的网格位置，则正应力分量的位置将作为中心点.为了得到一个对称的力矩张量源，将剪应力增量均匀分布在真实矩张量源位置附近的四个应力网格点上.因此，在矩张量源的真实位置周围总共有12个相邻的网格点，这些网格点用剪应力分量数值实现.作用于交错网格节点i、j、k(即正应力分量的网格位置)的矩张量源的完整公式如式(13)(Shi et al.，2018)：

(13)

其中V=Δx·Δy·Δz是网格单元的有效体积，Δt是时间间隔.由于应力分量的时间导数用于黏弹性动力学方程，所以使用矩张量的时间导数.

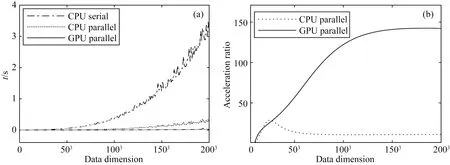
图1 运算效率对比(a)计算时间；(b)加速比.Fig.1 Comparison of calculation efficiency(a)Calculation time;(b)Acceleration ratio.

1.2 矩张量波形反演

微地震震源矩张量反演方法有很多，包括采用全波形反演或集中考虑特定的体波相位(如P波和S波)的反演方法等.本文使用全波形反演来估计黏弹性VTI介质中的微地震震源的矩张量，用伴随状态法计算目标函数的梯度.

目标函数采用L2范数：

(14)

其中dpre(m)是模拟波场记录，dobs是观测记录.采用伴随状态法计算目标函数相对于模型参数的导数∂F(m)/∂m(Michel and Tsvankin，2014)，根据Kim等(2011)可获得目标函数相对于矩张量元素的导数：

(15)

其中xs是震源位置，T是记录时间，ε+是伴随应变张量，S是震源时间函数.矩张量M的梯度只需计算在震源位置的伴随应变张量.

(16)

其中：

(17)

由于式(16)可以将波场解耦为衰减项和频散项，所以在波场反传时，保持频散项符号不变，同时将衰减项对应的符号改变可以补偿波场传播过程中损失的能量，即将式(17)修改为：

(18)

为了克服反传过程中高频噪声的影响，本文使用巴特沃兹低通滤波器在波数域对波场衰减项进行滤波处理(唐杰等，2021).对波场进行滤波时不应对传播算子信号进行滤波(Zhu and Carcione，2014)，需要将传播算子从频散项中分离，并加入低通滤波器，式(18)变为：

×[cos(πγij)(-∇2)γij-(Cij/ρ)-0.5sin(πγij)

(19)

对于微地震震源机制反演的研究，评估和量化反演参数的不确定性也是非常重要的，震源机制反演标准化误差由式(20)给出：

(20)

2 各向异性黏弹性VTI介质微地震正演

2.1 衰减各向异性对正演结果的影响

为了表征衰减的各向异性，Zhu和Tsvankin(2006)根据Thomsen参数(Thomsen，1986)的思路提出一组Thomsen型衰减参数(Thomsen-style notation for attenuation)，包括两个参考各向同性参数(QP0、QS0)与三个无量纲参数(εQ、δQ和γQ).QP0与QS0为分别表征对称(垂向)方向P波和SV波品质因子，参数εQ表征P波衰减各向异性强弱，作用与Thomsen参数中的ε类似，参数γQ表征SH波的衰减系数在水平方向与垂直方向的差异，作用与Thomsen参数中的γ类似，参数δQ在描述P波垂直方向衰减各向异性变化的快慢程度，与描述P波速度各向异性的δ相似.描述SV波衰减各向异性的σQ参数受Thomsen参数和Thomsen型衰减参数控制，即SV波衰减与ε、δ、εQ和δQ有关，σQ非独立参数.εQ、δQ、γQ、σQ分别为：

(21)

设置一个均匀模型进行波场模拟，分析衰减各向异性对正演结果的影响，模型大小为1000 m×1000 m×1000 m，网格间距10 m，网格点数100×100×100，模型参数为：纵波速度为2.42 km·s-1，横波速度为1.4 km·s-1；品质因子QP为35，QS为30；速度各向异性参数ε=0.4，δ=0.15，γ=0.1；衰减各向异性参数εQ=-0.125，δQ=0.94，γQ=-0.1.

随角度变化的纵横波速度如图2a中的实线和虚线所示，P波衰减系数与SV波衰减系数随角度变化分别如图2b、c所示.VTI介质中纵横波速度和衰减均呈现各向异性特征，图2d为弹性波与黏弹性波场快照对比，震源采用位于模型中心的主频为35 Hz的Ricker子波，时间步长为0.4 ms，震源采用爆炸源，图中四部分分别为弹性波、仅考虑频散项、仅考虑衰减项和黏弹性波，从图2d中可以看出，相对于弹性波，仅考虑频散项只有相位的延迟，仅考虑衰减项只有振幅的减小，而黏弹性介质中的波场既有相位的延迟又有振幅的减小.

图2 各向异性介质参数分析(a)速度各向异性，其中实线为P波，虚线为SV波；(b)P波衰减各向异性；(c)SV波衰减各向异性；(d)波场快照.Fig.2 Analysis of media anisotropy parameters(a)Velocity anisotropy.Solid curve is P-wave,and dashed curve is SV wave;(b)P-wave attenuation anisotropy;(c)SV wave attenuation anisotropy;(d)Wave field snapshot.

分别进行无衰减、各向同性衰减和三个各向异性衰减模型(参数如图3标注所示)正演模拟，获得0.15 s时刻的垂直速度分量波场快照如图3所示，其中图3a为无衰减波场快照，图3b为各向同性衰减波场快照，图3c、d、e分别为三个各向异性衰减模型的波场快照，图3f、g、h分别为各向异性衰减与图3b各向同性衰减的差值.在距震源约280 m位置处观测点获得0.25 s波场记录如图4b，其对比曲线如图4c.在各向同性介质中，爆炸源只产生P波，而从图3a可以看出，在各向异性介质中爆炸源同样会产生S波.除速度各向异性参数外，三组衰减各向异性参数均对波场具有一定影响.εQ表征P波在水平方向和垂直方向的衰减系数差异，0.12～0.17 s时间段曲线f存在起伏，即P波衰减受到各向异性影响，与各向同性衰减产生了差异；δQ为连接P波水平方向和垂直方向速度的过渡参数，也对P波衰减各向异性存在影响，在0.12～0.17 s的时间段曲线g存在起伏；而γQ表征SH波的衰减各向异性，在P波段曲线h基本无起伏，仅在0.18～0.25 s时间段的S波记录中曲线h存在起伏.在各向异性衰减VTI介质的波场模拟中，应当综合考虑多个各向异性参数的影响.

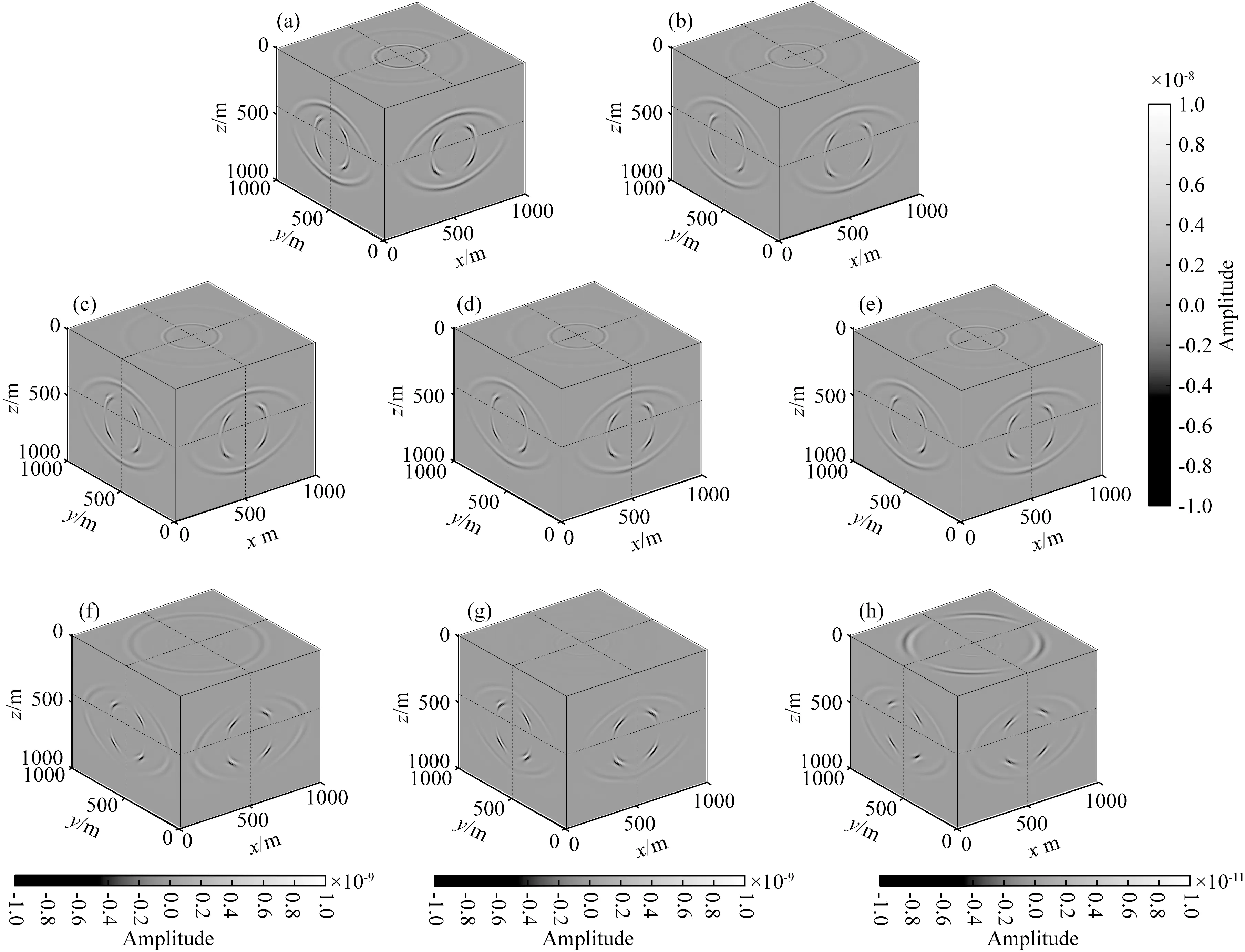
图3 介质参数对波场的影响(虚线为截面位置)(a)Q =∞；(b)εQ=0，δQ=0，γQ=0；(c)εQ=-0.3，δQ=0，γQ=0；(d)εQ=0，δQ=0.4，γQ=0；(e)εQ=0，δQ=0，γQ=0.4；(f)(c)—(b)；(g)(d)—(b)；(h)(e)—(b).Fig.3 Influence of media parameters on wave field (the dashed lines are positions of sections)

图4 介质参数对地震记录的影响(a)观测系统；(b)地震记录；(c)地震记录间差异.Fig.4 Influence of media parameters on seismic records(a)Observation system；(b)Seismic record；(c)Difference between seismic records.

2.2 不同类型震源机制正演结果

利用图2所采用的模型参数，模拟不同类型震源在黏弹性VTI介质中的波场传播，选用的震源机制如表1中所示，图5a为MISO震源的结果，图5b为MDC震源的结果，图5c为MCLVD震源的结果，图5d为混合类型震源MCOMBO的结果，不同类型震源计算得到的波场快照明显不同.MISO源在各向同性介质当中只能激发出P波，但在各向异性介质当中既能激发出P波又能激发出S波.MISO源激发出的P波能量要明显强于S波.非各向同性震源激发的信号中S波振幅和能量较大，考虑到微地震信号能量较弱，信噪比较低，P波可能会淹没在噪声中，在微地震监测中应考虑S波的拾取与利用；不同机制震源激发的信号在不同方向强弱不同，极性也存在差异，在成本的限制下应尽量考虑多口不同方位井进行多分量信号采集.

图5 均匀黏弹性VTI介质中不同类型源的波场快照(虚线为截面位置)(a)MISO；(b)MDC；(c)MCLVD；(d)MCOMBO.Fig.5 Wavefield snaps of different sources in a homogeneous viscoelastic VTI media(dashed lines are the positions of sections)

考虑断层面与[x，z]坐标平面重合的位错源，根据Aki和Richards(2002)提及的方法，若介质为VTI介质，则点位错源的矩张量可由式(22)计算得到：

(22)

图6给出了不同θ角度的纯剪切源的震源机制沙滩球与钻石图，当θ=30°或者θ=60°时，断层面不是位于VTI介质对称平面内，由图可知纯剪切错动在各向异性介质中仍然可能产生非DC成分，见表1的结果.当θ=0°或者θ=90°时，断层面位于VTI介质对称平面内，纯剪切源不会产生非DC成分，仍然为双力偶机制.

利用图2所采用的模型参数，加载图6中的位错源，图7给出了均匀黏弹性VTI介质中不同方向(由角度θ定义)位错源的垂直速度分量波场快照，不同的θ角度会导致振幅大小和极性分布发生明显的变化.背景介质各向异性强弱和断层面的几何位置等参数都会影响非DC成分，这种非DC成分也能够反应震源区的各向异性信息.

图6 VTI介质不同θ角度的位错源震源机制沙滩球与钻石图(a)θ=0°；(b)θ=30°；(c)θ=60°；(d)θ=90°.Fig.6 Focal mechanism beach balls and diamond plots of dislocation sources with different θ angles in VTI media

图7 均匀各向异性黏弹性VTI介质中不同方向(由角度θ定义)位错源的vz分量(虚线为截面位置)(a)M0°；(b)M30°；(c)M60°；(d)M90°.Fig.7 Component vz of different direction (defined by angle θ)dislocation sources in homogeneous viscoelastic VTI media (dashed lines are positions of sections)

基于常Q模型的分数阶拉普拉斯本构方程给出了一阶速度-应力方程中相应的包含震源机制影响的时域黏弹性VTI介质波动方程，通过波场模拟可以发现介质的衰减各向异性以及震源机制将使记录的波场更为复杂，速度各向异性会对记录的不同方位的地震波走时产生影响，衰减各向异性会对记录的地震波的行程时间(频散的影响)和振幅(衰减的影响)等参数产生影响，从微震数据中分析衰减各向异性有助于表征水力压裂中的裂缝特性；由速度和衰减各向异性引起的行程时间、幅度以及波形的变化可用于评估地下介质各向异性的强度.

3 各向异性黏弹性VTI介质震源机制反演

3.1 速度与衰减各向异性参数对反演的影响

为了验证各向异性黏弹性介质中震源机制全波形反演方法的有效性，建立三层黏弹性VTI介质模型，如图8a所示，模型尺寸为1000 m×1000 m×1000 m，各层的参数如表2所示，第一层和第三层为各向同性衰减的VTI介质，代表储层的上覆和下伏地层，由于不含孔隙流体，其衰减呈现各向同性，第二层为各向异性衰减的VTI介质，代表含孔隙流体的页岩地层，在该层进行水力压裂.该模型采用10 m的网格间距进行离散，震源位于模型中间位置，源函数是主频35 Hz的Ricker子波，观测系统如图8b，在震源周围设置三口垂直井，井中每50 m放置一个检波器，共60个检波器.通过正演模拟可以获得检波器位置的三分量微地震数据，不含噪声的记录如图9所示.

图8 (a)模型；(b)观测系统Fig.8 (a)Model；(b)Observation system

图9 井中地震记录(a)vz；(b)vy；(c)vx.Fig.9 Borehole seismic record

表2 模型参数Table 2 Model parameters

采用全波形反演方法可以获得黏弹性各向异性介质中的矩张量，反演时对第二层介质采用的模型参数如表3所示，其中A8为对模型介质参数进行高斯平滑的情况，因此震源区参数未发生改变.采用的震源机制MCOMBO如图10a所示，震源机制各分量见表1，其震源机制成分Lune图如图10b所示(Tape and Tape，2013)，文中矩张量反演初始值统一使用随机数组Minitial，见表1.

表3 反演采用的模型参数Table 3 Model parameters used in inversion

图10 本文采用的震源机制(a)沙滩球；(b)Lune图.Fig.10 Focal mechanism used in the paper(a)Beach ball;(b)Lune graph.

图11给出了采用不同介质参数反演目标函数随着迭代次数的变化情况，随着迭代次数的增加，目标函数都呈下降趋势，其中A1采用黏弹性各向异性介质模型，目标函数迭代后值最小，说明模拟波形与观测波形匹配得最好；A2采用弹性各向异性介质模型，忽略了衰减的影响，模拟波形的振幅与观测波形的振幅会存在差异，导致目标函数值迭代后相对较大；存在其他参数误差时，目标函数值迭代后相对无干扰时均有一定程度的升高.

图11 采用不同介质参数条件下的目标函数随迭代次数的变化Fig.11 Variation of the objective function with the number of iterations under different media parameters conditions

图12a为采用不同介质参数得到的反演矩张量的各个分量，图12b为分解得到的不同成分.由图可知采用黏弹性各向异性介质参数能够得到正确的反演结果，而速度或者Q值存在误差时会导致反演结果出现较大的偏差，衰减各向异性误差也会影响反演结果.图12c为不同介质参数条件下反演得到的震源机制沙滩球以及震源机制偏差，横轴为选取不同介质参数的情况，纵轴为反演结果的偏差.由图可知采用黏弹性各向异性介质模型能够获得正确的反演结果，本文方法在介质参数正确的情况下能够准确反演震源机制；采用弹性各向同性介质模型或者速度存在误差时，震源机制的反演结果会存在误差，结合图2及图3的分析可知ε、δ和γ控制水平纵波速度和横波速度偏离垂直方向的变化，这些参数的误差可能会改变某些接收器记录信号的到达时间和振幅，速度以及各向异性参数都会影响反演震源机制各分量的百分比.此外模型误差(如速度结构、衰减等相关的误差)的影响会随着距离的增加而增大，从而对反演结果产生不利影响，采用距离震源区较近的观测井数据能够减少此误差.

图12 不同介质参数时震源机制反演结果(a)矩张量；(b)成分；(c)震源机制沙滩球.Fig.12 Inversion results of focal mechanism with different media parameters(a)Moment tensor;(b)Component;(c)Focal mechanism beach ball.

3.2 噪声的影响

观测数据中的高斯噪声会在地震记录中造成严重的扭曲，噪声主要影响振幅，进而会影响矩张量的反演结果.为了分析数据中的噪声对微震震源机制反演的影响，在合成波形中加入不同信噪比的噪声.图13给出了添加不同噪声水平的垂直分量地震记录和单道三分量记录，当信噪比低于1时，地震记录受到大量高频成分噪声的干扰，图14为不同信噪比下反演目标函数迭代变化，存在噪声时合成记录无法与含噪信号完好匹配，伴随应变张量受到影响，目标函数值出现升高.

图13 不同信噪比条件下垂直分量地震记录及三分量单道记录对比(a)SNR=5；(b)SNR=1；(c)SNR=0.5；(d)SNR=0.1；(e)vz；(f)vy；(g)vx.Fig.13 Comparison of vertical component and three-component single-trace records under different SNR conditions

图14 不同信噪比条件下目标函数随迭代次数的变化Fig.14 Variation of the objective function with the number of iterations under different SNR conditions

图15a为采用不同噪声水平得到的反演矩张量的各个分量，图15b为分解得到的不同成分.图15c给出了不同信噪比条件下的震源机制反演结果，横轴为选取不同信噪比的情况，纵轴为反演结果的偏差.反演时采用了黏弹性各向异性介质模型，由图可知全波形反演方法具有一定程度的抗噪性.信噪比较高时尽管振幅值中增加了噪声，但结果仍具有较高的精度.如果使用较少的观测数据或者信噪比过低时，误差也会相应增大.

图15 不同噪声水平下震源机制反演结果(a)矩张量；(b)成分；(c)震源机制沙滩球.Fig.15 Inversion results of focal mechanism with different levels of noise(a)Moment tensor;(b)Component;(c)Focal mechanism beach ball.

3.3 观测系统的影响

三维波形反演应用于微地震数据的一个主要挑战是有限的源-接收器覆盖范围(数据孔径)，检波器分布对矩张量反演结果的可靠性有很大影响，因此微地震监测项目的设计应考虑到这一点.表面阵列有一个更大的孔径(即大偏移距深度比)，部署成本通常也更低，能够采集到多方位的地震信号，但由于微地震信号能量弱、衰减快，地表监测的主要问题是相对井监测记录信噪比较低，本节只讨论井监测观测系统的影响.井下观测通常使用三分量传感器，能够获得更高信噪比的微地震信号，这将提高反演结果的可靠性.但是如果需要钻新的井，则井下监测可能比地表监测昂贵得多，另外由于大多数井的一维特性，它们比设计良好的表面阵列采集的焦球信息更少，反演结果更容易受震源位置与井的关系的影响.本节采用不同数目、方位垂直井和不同检波器进行反演，分析井下观测系统对微地震震源机制反演的影响.

图16 不同观测系统下矩张量各分量反演结果(a)走滑断层；(b)倾滑断层；(c)正断层；(d)逆断层.Fig.16 Inversion results of moment tensor components with different observation systems(a)Strike-slip fault;(b)Dip-slip fault;(c)Normal fault;(d)Reverse fault.

图17给出了不同检波器分布条件下的震源机制反演结果，横轴为选取不同震源机制的情况，纵轴为反演结果的偏差.由图可知对于不同的震源机制单井三分量和单井单分量反演得到的偏差较大，震源机制沙滩球与真实值存在较大的差异.三井三分量记录反演的偏差高于三井单分量，其原因为噪声和Q值误差综合干扰，导致三分量记录受到的影响高于单分量记录，若仅考虑噪声影响时，三分量记录抗噪性高于单分量记录.在垂直横向各向同性地层中钻取的垂直井中，利用单井微震观测资料，对于地震矩张量的六个独立分量不能唯一地进行反演.通过假设震源的某些物理特性使原本独立的矩张量分量相互关联(如拉伸断裂假设等)，使矩张量反演正则化，有助于减少反演结果的模糊性(Grechka et al.，2016).

图17 不同观测系统下矩张量反演结果沙滩球(a)走滑断层；(b)倾滑断层；(c)正断层；(d)逆断层.Fig.17 Beach balls of moment tensor inversion results with different observation systems(a)Strike-slip fault;(b)Dip-slip fault;(c)Normal fault;(d)Reverse fault.

如果微地震事件靠近监测井，如图18a中1号井和2号井，由于能够采集到的更多的焦球信息，如图18b所示通过全波形反演可以从单井数据集中获得完整的矩张量(如1号井和2号井)；当观测井位于远场范围时(如3号井和4号井)，仅靠单井资料无法完成矩张量反演，因此获得足够的震源辐射花样信息对于震源机制反演具有重要的意义(Song and Toksöz，2011).

图18 (a)观测系统；(b)不同方位井记录下矩张量反演结果沙滩球Fig.18 (a)Observation system；(b)Beach balls of moment tensor inversion results with different azimuth borehole records

4 结论

本文提出了黏弹性VTI介质中震源矩张量反演方法.首先推导了黏弹性VTI介质波动方程并采用GPU并行伪谱法正演模拟微地震记录，然后通过全波形反演算法获得了微地震震源机制，并通过实验测试验证了该方法的有效性，得到的主要结论包括：

(1)页岩油气储层通常具有各向异性或者由于水力压裂而产生各向异性，基于常Q模型和分数阶拉普拉斯算子推导的黏弹性VTI介质波动方程能够描述速度各向异性和衰减各向异性，更符合地下介质的实际情况.正演结果表明介质的衰减各向异性以及震源机制将使记录波形更为复杂，分析衰减各向异性有助于表征水力压裂中的裂缝特性.

(2)震源机制全波形反演需要获得伴随波场计算矩张量梯度，由于介质具有各向异性和黏弹性，在计算伴随波场时需要进行衰减补偿，本文推导的波动方程能够在反传过程对波场进行各向异性衰减补偿，提高矩张量梯度计算的准确性.

(3)全波形反演方法可以有效反演黏弹性VTI介质中的震源矩张量.数值测试证明采用黏弹性各向异性介质模型能够获得正确的反演结果，将黏弹性各向异性添加到矩张量反演中可以帮助详细研究非DC成分是否真的存在或是由计算误差引起的.反演过程中的模型参数误差、观测数据噪声和观测系统等也会对反演结果造成影响，获取良好的地层介质参数和设计合理的观测系统能够更准确地反演震源机制以评价压裂效果.

除黏弹性各向异性外，微地震震源机制的反演还涉及许多其他问题，如震源定位结果、震源时间函数和模型网格大小等因素的影响，本文不做进一步展开.由于波形反演效果依赖背景介质模型的可靠性，为提高抗干扰能力可以在反演过程中同时对震源机制和模型参数联合反演，以减少模型参数不准确带来的误差，但这也会带来参数串扰问题以及更大的计算量，有待进一步研究.