大型铸锭的宏观偏析及其数值模拟

张 帆 殷子豪 杨宇乾 仲红刚

（上海大学先进凝固技术中心，上海 200444）

大型铸锭被广泛应用在核电、航空航天、船舶制造等领域。比如百万千瓦级核电机组的核心组件形状复杂，需整体加工，需要百t以上的铸锭。到2020年，我国电力机组大型铸锭的总需求量超过了40万t，航空航天、船舶制造等对大型铸锭的需求量也在增加。大型铸锭的生产水平直接影响国家大型装备制造业的发展，是衡量一个国家综合国力的重要标准［1-3］。

大型铸锭因其体积大、凝固时间长（甚至长达100 h以上），元素的溶质再分配系数、不同部位的凝固速度、流动状态和温度分布差异都非常大，极易产生缺陷，尤其是宏观偏析，致使铸件性能降低甚至报废［4］。宏观偏析的形成机制和控制一直是凝固理论的重要部分，因此研究宏观偏析的形成机制并进行预测和控制，特别是从大型铸锭的生产源头控制宏观偏析对提高大型铸锭的均质性和成材率具有重要意义。但是，大型铸锭一般重达几十t以上，影响凝固过程的因素极其复杂，直接通过试验进行研究，周期长且成本不可控。自20世纪60年代研究者采用有限差分法成功模拟了铸件凝固过程的温度场以来，数值模拟在试验研究和工业应用中逐渐发展，先后开发了多种宏观偏析的数学模型，并得到应用。

本文分析了大型铸锭宏观偏析的形成机制和影响宏观偏析的因素，介绍了研究铸锭宏观偏析的方法，阐述了研究凝固过程中宏观偏析形成的数值模拟技术的进展，归纳了现有的宏观偏析的数学模型及其特点，总结了目前宏观偏析数值模拟所存在的问题。

1 宏观偏析形成机制及影响因素

1991年，为了研究大型铸锭宏观偏析及组织的分布特点和形成机制，Blondeau等对65 t低碳钢铸锭进行了解剖，如图1所示，清晰地观察到铸锭底部等轴晶锥形沉积区的负偏析，铸锭上部则存在显著的正偏析，柱状晶区和等轴晶区的分界处（约1/2半径区域）存在A型偏析和分布在中心等轴晶区的V型偏析［5］。20世纪80年代，上海重型机械厂解剖了一个55 t的大钢锭，研究了其中的缩孔缩松和碳元素分布［6］。近年来，Pickering等［7］解剖了一个12 t的铸锭，通过X 射线荧光光谱分析仪研究了其中的元素分布。这些解剖试验都为宏观偏析的形态和分布特点提供了直接证据。

图1 65 t低碳钢铸锭纵向宏观组织、碳元素宏观偏析（a）及其硫印图（b）［5］Fig.1 Longitudinal macrostructure，macrosegregation of carbon elements（a）and sulfur print（b）of 65 t low carbon steel ingot［5］

早在20世纪60年代，金属凝固过程中的溶质再分配现象就被提出，认为产生宏观偏析的主要原因是高溶质的残余液相相对于低溶质的固相骨架的运动［8］。大型铸锭中不可控制的多尺度多相流动加剧了这种相对运动，产生了各种不同特征的偏析。大型铸锭生产中造成固液两相相对运动的主要原因有［9］：

（1）浇注过程、搅拌、外加电磁场等引起的强制流动；

（2）冷却过程中固液两相的收缩及凝固收缩引起的液相补缩流；

（3）残余液相温度和成分分布不均匀导致密度差异引起的自然对流；

（4）等轴晶和破碎固相碎片的运动；

（5）由热应力、收缩应力、静压力等引起的糊状区固相骨架变形；

（6）气泡、夹杂物的运动。

大型铸锭中不同特征的宏观偏析是如何形成的问题一直是国内外学者研究和争论的焦点。对A型偏析的早期研究认为，在铸锭上部，当液相流速大于固-液界面的推进速度时，局部低温区会发生重熔，熔化通道在后续的凝固过程中被富溶质液体填充，从而产生A型偏析。由此可见糊状区液相流动对A型偏析的产生有重要影响，且枝晶重熔是形成A型偏析的主要原因［10-13］。但Li等［13］采用混合凝固模型计算了2.45 t钢锭的宏观偏析，包括之前的工作［14］，并没有发现明显的重熔现象，且随着等轴晶率的降低至零，仍有A型偏析存在，说明枝晶重熔和等轴晶的形成并不是产生A型偏析的必要条件。他们认为，A型偏析起源于流动不稳定区域，等轴晶的形成加剧了柱状晶尖端附近液相的流动，A型偏析在这里产生和发展。Cao等［15］建立了一种包含夹杂物上浮的宏观偏析模型，模拟结果显示，具有足够数量且达到一定直径的夹杂物能改变局部区域液相的流动状态并破坏糊状区，然后通过溶质富集和相邻夹杂物维持夹杂物与糊状区的相互作用，从而产生A型偏析，因此认为夹杂物上浮促进了A型偏析的形成。

V型偏析的形成机制较为复杂，目前普遍认为形成于铸锭凝固后期，铸锭中心等轴晶组成的骨架结构在对流和凝固收缩作用下变形塌陷，高溶质的液相填充在其中，因此形成正负偏析的不连续分布［16］。Suzuki等［17］认为，V 型偏析主要受热状态、重力作用和枝晶形态等因素的影响，其中重力对V型偏析没有直接影响，但重力作用引起的枝晶形态和成分分布变化对V型偏析的形成有较大影响。另一种理论认为，在凝固后期，铸锭顶部所谓“小型铸锭”的形成及其内部发生的等轴晶沉降可能会导致V型偏析的产生。这种理论的提出与连铸有关，在凝固后期，由于某些枝晶生长过快产生局部“搭桥”，阻断了上部剩余高溶质液相的流动，从而形成溶质富集的“小型铸锭”凝固现象，因此要形成“小型铸锭”需要高径比较大的细长形铸锭［18］。Li等［13］通过数值模拟获得了“小型铸锭”中正负偏析之间的不连续分布，且其形态与V型偏析类似。但这种理论有一定的局限性，在当前的模型中，没有考虑其他影响V型偏析的重要因素，例如凝固收缩引起的补缩流和沿铸件中心线的糊状区枝晶的变形等。

Flemings等［16］认为，铸锭底部的锥形负偏析是低溶质的等轴晶或枝晶碎片在重力作用下沉降堆积而形成的。虽然高溶质含量残余液相的流动对铸锭底部负偏析也有影响，但等轴晶或枝晶碎片的沉降仍起决定性作用。刘东戎等［19］模拟了考虑固相移动和固相不移动条件下的宏观偏析，考虑固相移动时，铸锭底部产生明显的负偏析，同时顶部正偏析程度增大。Kumar等［20］建立了考虑等轴晶形貌与运动的三相模型，对数值模拟结果与实际6.2 t钢锭底部负偏析的比较表明，等轴晶晶粒形貌对负偏析形成有重要影响。

产生铸锭顶部正偏析的根本原因在于选分结晶现象，随着凝固的进行，溶质不断在残余液相中富集，而溶质密度比基体金属低，导致残余液相密度减小，因浮力而向上流动，最终高溶质的液相在铸锭顶部凝固，顶部产生正偏析［4］。目前的研究认为，凝固初期铸锭底部等轴晶沉积堆的形成对顶部正偏析也有影响。其主要原因是，凝固初期，等轴晶在大环流下沿固-液界面沉入铸锭底部，同时加速了热溶质对流，尤其是中心的流速，使铸锭顶部正偏析加重。

基于细化凝固组织以控制宏观偏析的思路，上海大学先进凝固技术中心提出的脉冲磁致振荡技术（pulsed magneto-oscillation，PMO）已成功应用于连铸生产［21-22］。并在此基础上提出了冒口脉冲磁致振荡技术（hot-top pulsed magnetooscillation，HPMO），通过电磁效应，在固-液界面产生振荡，促进初生晶核的形成、脱落、运动、下落，最终实现晶粒细化，同时其产生的与自然对流反向的强制流动可大大减轻铸锭的宏观偏析，实现均质化［23-27］。李辉成等［28-30］研究发现，HPMO可使铸锭凝固组织细化，锭身成分均匀。但其“结晶雨”效应会使大量晶粒从铸锭中心向下运动并沉积，加重铸锭顶部的正偏析。由于铸锭冒口一般会被切除，这一技术的工业应用几乎不会受影响。

2 研究铸锭宏观偏析的主要方法

目前，国内外研究铸锭宏观偏析的主要方法有铸锭解剖、实验室模拟和数值模拟等。直接解剖的准确度最高，但对于大型铸锭，其所需材料量大、生产周期长、测试难度大且成本高，因此国内外较少通过解剖大型铸锭来研究宏观偏析。实验室多采用低熔点合金和NH4Cl-H2O溶液模拟，能在一定程度上直观反映其凝固过程和成分分布。但由于其物性参数与钢差距较大，实用性较差。随着计算机技术的高速发展，数值模拟可实现中间过程的可视化，且成本低，已被用于宏观偏析的研究。

2.1 铸锭解剖

大型铸锭凝固周期长，对流和传输过程复杂，在凝固过程中难以直接观察到宏观偏析的形成过程，因此早期对宏观偏析的研究以解剖试验为主。自法国Creusot Loire公司对65 t大钢锭进行解剖试验以来，国内外研究者也进行了一些铸锭的解剖试验。Kim 等［31］对13、25、54、430 t的大钢锭进行了解剖，分析了横截面的成分分布，研究了铸造工艺和成分对钢锭宏观偏析的影响。日本制钢所［32］对650 t核电低压转子用大型钢锭进行了解剖，获得了纵截面的成分分布。2011年，中国第二重型机械集团公司联合太原科技大学对234 t钢锭进行了解剖，研究其显微组织和元素偏析，期望找到提高钢锭质量的途径［33-34］。2014年，中国科学院沈阳金属研究所的李依依院士和李殿忠教授等［35］对0.5 ～650 t钢锭进行了解剖研究，发现夹杂物的上浮与A型偏析相关，说明钢水的洁净程度对A型偏析的产生有重要影响。

2.2 实验室模拟

实验室模拟的方法多采用低熔点合金或水溶液，根据相似性原理模拟铸型中的流场分布、夹杂物运动、合金元素分布等。Bennon等［36］最早在NH4Cl-H2O溶液中观察到A型偏析。清华大学董超［37］采用甲基蓝模拟钢液中的碳元素，设计了浇注过程中碳元素传输分布的物理模拟（水模拟）平台，并采用光纤传感器和传感器阵列测定了水中甲基蓝的浓度和溶质的空间分布。

2.3 数值模拟

20世纪70年代以来，大量计算机仿真软件被开发和应用，逐渐开发出了成熟的商用模拟软件，包括ANSYS和ProCAST等。利用相关软件可预测大型铸锭不可控的多尺度多相凝固过程，包括熔化和凝固的相变模拟、热传导和热对流的传热模拟、自然对流和强制对流的流动模拟、各溶质元素析出和扩散的传质模拟等，大幅度缩短了试验周期，加快了大型铸锭宏观偏析的研究过程。

3 宏观偏析数学模型

20世纪60年代初，丹麦学者Forsund首次将有限差分法应用于铸件凝固过程的传热模拟计算，为研究者提供了新的研究思路。此后也有人对凝固过程的数值模拟进行了研究［38］。1958年，Kirkaldy等［39］提出了简化的枝晶模型，首次模拟了一维枝晶生长方式的成分分布。但因该模型仅考虑了凝固和溶质再分配，并未考虑枝晶间熔体对流对溶质分布的影响，局限性很大。后来，Flemings等［40-42］在铸锭液相流动连续方程和简化的溶质传输方程的基础上，提出了著名的局部溶质再分配方程：

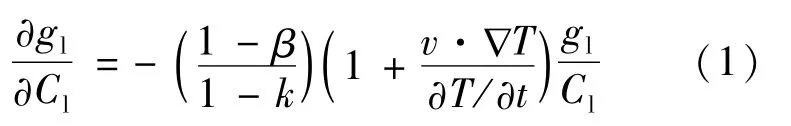
式中：g1是液相分数；Cl是液相溶质分数；β是凝固收缩率；k是平衡分配系数；v是枝晶间液相流动速度；∇T是温度梯度；∂T/∂t是凝固速度，首次将枝晶间微观流动与溶质再分配联系起来，揭示了在一定凝固收缩率下流动对溶质分布的影响。不考虑枝晶间流动和凝固收缩时，就可简化为著名的Scheil方程。Mehrabian等［43］试验验证了局部溶质再分配方程的合理性，并逐步应用于三元合金体系。而后，Mehrabian等［44］在此基础上，通过引入Darcy定律将糊状区简化为多孔介质，以此来计算枝晶间液相的流速，成功模拟了Al-Cu合金中的A型偏析。虽然该模型没有整体求解温度场，并忽略了液相区-糊状区之间的相互作用，但为之后的研究者提供了思路。此后宏观偏析的数学模型得到了快速发展，多计算域模型、连续介质模型、体积平均模型、两相及多相模型相继被提出［45］。

多计算域模型需要对每个凝固区域（固相区、液相区和糊状区）建立不同的控制方程（质量、动量、能量及溶质守恒方程），并显式追踪各区域边界。Fujii等［46］首次使用多计算域模型来计算糊状区的温度分布，通过试验验证，成功模拟出通道偏析，并通过数值模拟结果调整钢液成分抑制通道偏析。多计算域模型需持续追踪各个区域的变化，凝固过程中各相界面的复杂性及边界网格重构，尤其是考虑复杂的枝晶形貌时，无疑大幅度增加了数值模拟的复杂性，所以之后多域模型没有得到广泛应用。

20世纪90年代，Bennon等［47］基于经典混合理论，建立了二元合金凝固时的传热、传质和动量的连续介质模型。他们使用Navier-Stokes方程来求解液相区流动，采用Darcy定理处理凝固过程中固相对残余液体的流动阻力，即不再区分液相区、固相区和糊状区，视整个凝固体系为一单域连续介质，溶质在固、液相中的浓度分布与液相率的关系通过平衡相图根据局部热力学平衡推得。Bennon等［36］基于这一模型成功模拟了NH4Cl-H2O溶液和Sn-Pb合金宏观偏析的形成过程。Sahani等［48］模拟了基于连续介质模型的Pb-Sn合金的温度场和溶质场，并进行了试验验证。Ni等［49-50］在之前工作的基础上，建立了考虑凝固过程中更多细节（成分过冷、凝固收缩等）的宏观偏析数学模型。这些数值模型的建立都说明宏观偏析数学模型取得了突破性进展。

Beckermann等［51］基于体积平均的方法提出了体积平均模型，将糊状区视为相互渗透的固液两相，同时糊状区固相对液相的流动阻力也采用Darcy定理处理，并通过NH4Cl-H2O溶液凝固试验，验证了他们提出的体积平均模型的可靠性。Gu等［52］基于之前的模型，建立了适用于预测多组元大型铸锭凝固过程中产生宏观偏析的模型，铸锭顶部的正偏析与实测结果吻合度较好，但铸锭底部负偏析与实测结果偏差很大，这是因为上述模型没有考虑等轴晶和枝晶碎片的运动对宏观偏析的影响。后来众多学者对体积平均模型进行了研究和补充修正。Schneider等［53］建立了多组元等轴晶-液相两相凝固模型，成功模拟出大型铸锭的宏观偏析。Voller等［54］基于体积平均模型提出了温度与溶质的局部点对点的耦合方案，巧妙地将复杂的微观尺度的模型耦合到了一般凝固模型中。

通过对各相区建立同一套控制方程，连续介质模型和体积平均模型显著降低了数值模拟的复杂性，推动了宏观偏析数值模拟的发展，在通道偏析、连铸的中心线偏析及模铸的顶部正偏析中有成功的应用。但连续介质模型和体积平均模型忽略了固相的移动，主要考虑了热溶质对流产生的偏析，对等轴晶沉降引起的负偏析及枝晶熔断碎片的上浮不能准确模拟。同时，连续介质模型和体积平均模型是在平衡凝固的假设条件下建立的，无法考虑非平衡凝固下的过冷、形核、枝晶生长等效应，与实际的凝固过程有差异。而金属的凝固过程不仅有熔体的复杂多尺度多相流动，还包含溶质扩散、晶粒形核长大及晶核的漂移沉降等微观过程。之后在体积平均模型的基础上，Ni等［55］建立了体积平均的两相模型，对于凝固体系中的液相与固相分别采用不同控制方程处理其传输过程，也考虑了形核、过冷等微观过程，并指出形核率对晶粒运动和宏观偏析的分布有显著影响。Li等［56］建立了考虑形核与生长、晶体沉降和凝固收缩的两相模型，模拟了53 t钢锭中宏观偏析的产生，并与实际结果进行对比，验证了模型的准确性。

在两相模型的基础上，Wang和Beckerman［57-59］建立了包含固相、液相和等轴晶的多尺度多相模型。Wu等［60］建立了液相-柱状树枝晶-等轴树枝晶混合的三相模型，综合考虑了晶体形核、枝晶生长、不同界面间的阻力和溶质传输等微观因素对宏观偏析的影响，并通过与一维经典算例的比较，验证了模型的准确性。2015年，Ahmadein等［61］提出了预测包含柱状树枝晶、等轴树枝晶等五相铸态组织的宏观偏析数学模型，并进行了一系列试验对模型进行验证，计算结果与试验结果比较一致，并能预测柱状晶向等轴晶的转变。多相模型中对固相进行了更加细致的描述，而不是简单地统一为一致的相，并综合考虑了铸造过程中的各种细节，能更准确地预测多种宏观偏析。但随着相数的增加，数学模型的建立越发困难，模型求解时间也增加，限制了其在大型铸锭数值模拟中的应用。

4 结束语

在大型铸锭宏观偏析的控制方面，近年来进行了大量的研究，目前有望得到工业应用的有多包合浇、层状铸造等。特别是近年上海大学先进凝固技术中心提出的HPMO已经过多次工业试验，能有效使大型铸锭的成分均匀化，大幅度降低宏观偏析。但大型铸锭工业试验难度大、成本高，导致HPMO等技术的工业试验和应用进展缓慢，因此合理应用数值模拟已成为推动宏观偏析控制技术发展和工艺优化的重要途径。

经过几十年的发展，大型铸锭宏观偏析的形成机制和数值模拟已取得了很大进展。然而关于A型偏析和V型偏析的形成机制目前尚无定论，还需做进一步的工作。宏观偏析的数学模型发展迅速，综合考虑的因素越来越多，考虑了溶质传输、形核、固相移动、夹杂物甚至各种组织转变等微观现象对宏观偏析的影响。但随着考虑的因素的增多，模型也越加复杂，计算求解量也越来越大，求解时间和成本大幅度增加。同时受大型铸锭体积的限制，计算网格不宜划分过细，只能采用较大的网格单元，这将导致难以模拟A型偏析和V型偏析。另外，宏观偏析的数值模拟需要大量的参数，比如合金的热物性参数、初始条件、边界条件等，参数的匮乏也降低了宏观偏析数值模拟的可靠性，需要进行大量的工作建立模型数据库。因此，如何快速、准确预测宏观偏析是未来宏观偏析数值模拟的重要发展方向。总之，宏观偏析的数值模拟仍有很多问题有待解决。