支撑辊倒角对热轧钢板板形的影响

2022-01-25贾俊彪吴成军

上海金属 2022年1期

贾俊彪严彪吴成军

（1.同济大学材料科学与工程学院，上海 200092；2.上海聚重金属材料科技有限公司，上海 200433）

四辊可逆式热轧机的支撑辊在轧制过程中承受有害弯矩［1］继而发生挠曲，造成支撑辊与工作辊之间的接触应力沿辊身方向分布不均，在支撑辊边部出现应力集中。应力集中区域在加工硬化、局部过度磨损、交变剪切应力的作用下，易出现疲劳裂纹并最终导致辊面剥落，造成支撑辊失效［2-3］。为解决这一问题，较为常见的方案是对支撑辊增加倒角设计或优化已有的倒角形状。通常采用影响函数法［4］或有限元软件计算［5］方法，分析不同倒角形状辊系应力分布，从而找到轧机辊系最佳的倒角形状。针对不同的轧机辊系，倒角形状有直线型［6］、圆弧型［7］、幂函数型［8］等。

目前业内普遍认为，优化支撑辊倒角有助于板形的控制，但有学者提出过大的支撑辊倒角长度可能会产生肋浪板形缺陷［9］。某企业2 800 mm中厚板轧机支撑辊倒角优化后，抗剥落性明显提高，但钢板中间浪形缺陷的出现概率大幅度上升，严重影响了产品质量（如图1所示）。本文通过有限元模拟轧制分析不同支撑辊倒角形状下钢板横截面形状的差异及其对钢板板形的影响，为解决钢板中间浪形缺陷提供依据和新途径。

图1 热轧钢板中间浪形缺陷Fig.1 Center buckles of the hot-rolled steel plate

1 有限元模型的建立

根据轧制板形控制理论，钢板中间浪形与其轧制过程中横向变形不均匀有关，不均匀程度可以用钢板凸度以及轧制道次间钢板比例凸度的变化程度来描述［10］，因此模型重点关注轧制后钢板的横截面形状，并辅以沿辊身轴向接触应力的分布来讨论支撑辊倒角对接触应力分布的影响。为简化模型，假设轧辊、钢板都为均质材料，不施加复杂的温度场，同时假设轧辊不发生磨损。

根据实际生产数据，使用Abaqus软件创建轧制过程的三维模型，根据轧机的对称性，只取轧机及钢板的1/4部分进行建模（如图2所示），部件包括支撑辊、工作辊以及钢板，具体几何尺寸和材质设置如表1所示。为了比较，选用3种不同倒角的支撑辊以及3种不同宽度的钢板。

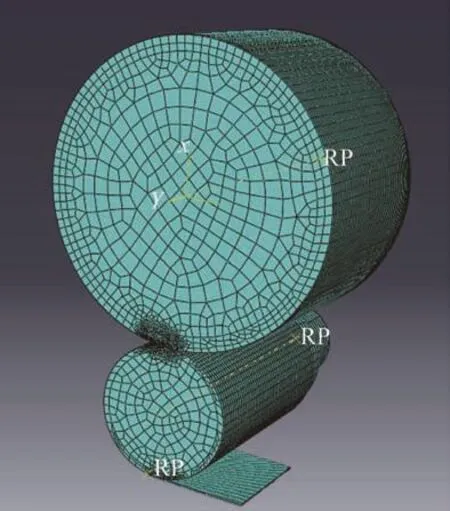
图2 Abaqus轧制模型Fig.2 Rolling model in Abaqus

表1 Abaqus模型部件尺寸及材料属性Table 1 Parts size and material properties in Abaqus model

3种支撑辊倒角均采用两段式倒角设计（如图3所示），分别为原始设计倒角（简称backup1型）、为解决支撑辊剥落问题而设计的优化倒角（简称backup2型）以及将backup2型倒角主倒角长度缩短的对比倒角（简称backup3型），具体尺寸如表2所示。从主倒角尺寸看，backup2、backup3、backup1型倒角长度依次减小，倒角长高比依次减小。

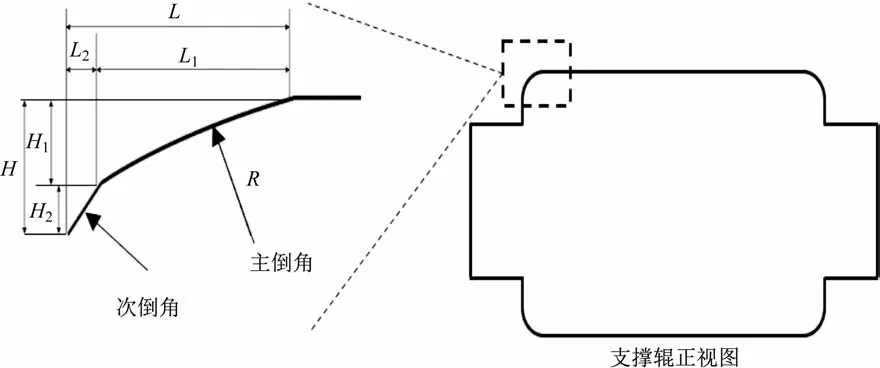
图3 支撑辊倒角示意图Fig.3 Schematic diagram of the backup roll chamfer

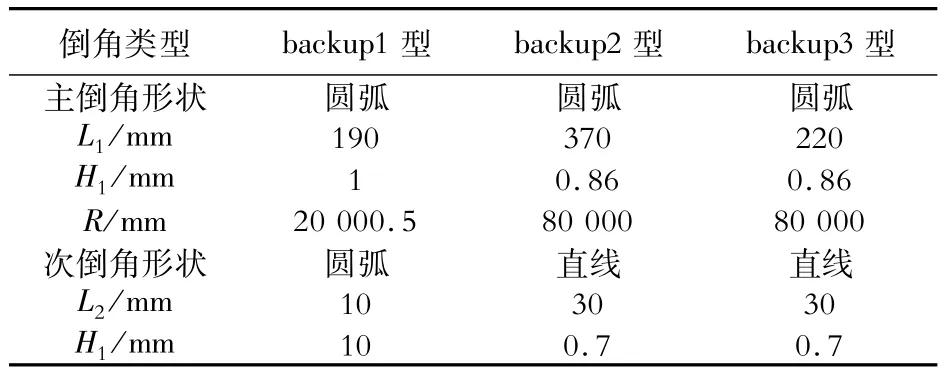
表2 支撑辊倒角尺寸Table 2 Size of the backup roll chamfer

在单元设计上，钢板的横截面形状是由轧制过程中工作辊的实际辊缝形状决定的，因此辊系变形的计算十分重要。二次单元因剪力自锁问题不适用于非线性接触的问题求解［11］，因此对于计算精度要求较高的轧辊表面接触区域，选用线性单元中应力和位移计算精度较高的8节点线性实体非协调单元（C3D8I），其余部分则使用计算成本更低的缩减积分单元（C3D8R），轧辊接触区的网格也进行细分。根据文献［8］和实际测量结果，将径向尺寸设置在2 mm内以保证计算精度。轧辊均设置为均质的弹性体，材料属性如表1所示，钢板设置为弹塑性体，流变应力参数按照实现20%～25%变形率进行设置。各部件间接触均设为硬接触，采用罚函数进行处理，摩擦因数设为0.25。约束方面，通过轧辊端部绑定刚性面来实现加载以及轧辊的转动［11］。模型计算分3步，先在支撑辊端部施加小载荷静压下实现部件接触，之后将该载荷增大至设定轧制力大小，最后在工作辊端部施加1 m/s的转动约束以及弯辊力以实现轧制模拟。

模型设置了3种轧制力（30 000、40 000、50 000 kN）、3 种板宽（1 500、1 800、2 100 mm）以及4 种弯辊力（1 800、2 000、2 300、2 500 kN）。使用Abaqus/Explicit模块进行轧制模拟计算。

2 模拟结果与讨论

图4为在2 100 mm板宽、1 800 kN弯辊力和50 000 kN轧制力条件下，3种支撑辊接触应力的轴向分布。从图4可知，支撑辊端部50 mm区域（大于次倒角长度）均未与工作辊接触，因此副倒角对本次结果没有影响，3种支撑辊接触应力均在倒角根部附近取得最大值，backup1、backup2、backup3型支撑辊的接触应力峰值分别为1 685、1 561、1 625 MPa，backup2 型的应力峰值最小，倒角根部附近的应力变化最平缓，说明随着倒角长度的增加，倒角长高比增大，支撑辊应力峰值降低，应力沿轴向分布更均匀，改善支撑辊受力的效果最好。这一规律与采用影响函数法计算的结果一致［12］。

图4 3种支撑辊接触应力的轴向分布Fig.4 Axial distributions of contact stress in the three kinds of backup rolls

根据板形控制理论，钢板板形良好的条件是钢板凸度的绝对值较小且道次间钢板比例保持不变［10］。当凸度和道次比例凸度变化为负值时，钢板可能出现中间浪形缺陷。

图5为在2 100 mm板宽、2 500 kN弯辊力和30 000 kN轧制力条件下，采用3种支撑辊轧制的钢板横截面厚度差。可以看出，采用backup1、backup2、backup3型支撑辊轧制的钢板在距离边部150 mm处的凸度（用C150表示）分别为－37、－75、－64 μm，结合倒角形状特点，说明随着倒角长度的增加，倒角长高比增大，钢板凸度减小。

图5 采用3种支撑辊轧制的钢板横截面厚度差Fig.5 Difference in the cross-sectional thickness of steel plates rolled by the three kinds of backup rolls

汇总不同试验条件下的钢板凸度，以轧制力、弯辊力、钢板宽度作为变量X，凸度作为响应Y进行响应曲面法（response surface methodology，RSM）分析，确定主要影响变量，结果如表3所示。

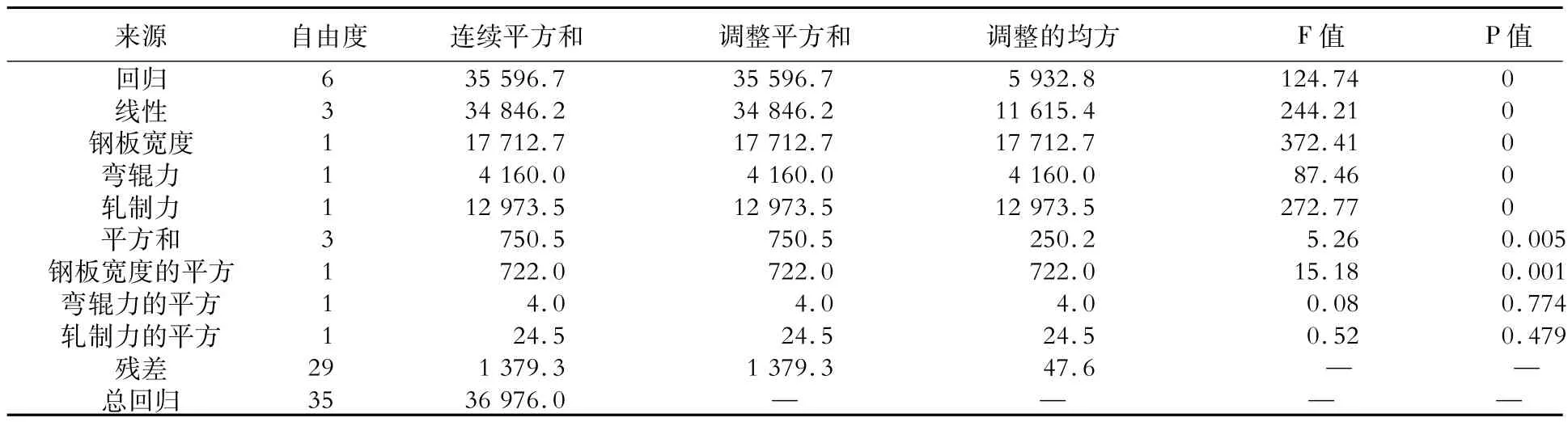
表3 板凸度C150的响应曲面法分析结果Table 3 Response surface methodology analysis result of the plate crown C150

根据各项因子的显著性分析可知，钢板宽度、宽度平方、轧制力、弯辊力的P值远小于0.05，说明是显著因素，因此可以选这4项作为参数，对钢板凸度C150进行线性回归，回归方程为：

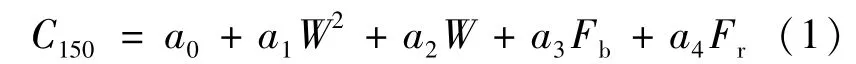
式中：a0～a4为各项系数；W为钢板宽度；Fb为弯辊力；Fr为轧制力。

表4为不同支撑辊条件下钢板凸度C150的线性回归结果（为方便讨论，对各自变量进行了归一化处理）。从表4可以看出，各条件下的拟合优度R2值均大于95%，验证了回归方程的有效性。回归方程的各项系数中，轧制力和弯辊力的系数变化很小，在不同轧制力、弯辊力条件下支撑辊倒角变化引起的板凸度C150变化基本相同；钢板宽度的系数变化较大，钢板越宽，支撑辊倒角变化引起的板凸度C150差异越大。以图5所示的轧制条件为例，改用backup2型支撑辊后板凸度减小并出现负值，可能产生中间浪形缺陷，从而解释了实际生产中使用backup2型支撑辊后中间浪形缺陷发生率升高的现象。相较backup2型，采用backup3型支撑辊对板凸度的影响较小。

表4 钢板凸度C150的线性回归结果Table 4 Linear regression result of the plate crown C150

根据上述板凸度的计算结果，进一步讨论不同支撑辊倒角对轧制过程中道次比例凸度变化的影响。道次比例凸度变化ΔCp是指某道次轧制前后钢板比例凸度的差值，计算公式为：

式中：H1、H2为道次入口、出口侧钢板厚度；Cr0、Cr1分别为道次入口、出口侧钢板凸度。

在相同轧制规程条件下，比较采用支撑辊A（原始设计）和支撑辊B（优化设计）条件下钢板最后一个轧制道次的比例凸度变化ΔCp，以A为参照，设ΔCr为某一工艺条件下采用支撑辊B后的板凸度变化量，则支撑辊B的道次比例凸度变化为：

根据式（3）可知，不同支撑辊之间道次比例凸度变化不同，该差异与ΔCr（支撑辊辊型、钢板宽度）、（H1－H2）/H1（道次压下率）成正比，与道次出口厚度H2成反比，即支撑辊辊型变化引起的板凸度变化越大，道次变形量越大，则钢板厚度越小，道次比例凸度变化量越大，板形变化也越大。由于ΔCr为负值，该板形易产生中间浪形缺陷。

3 板形控制

根据支撑辊倒角对钢板凸度以及道次比例凸度变化的影响规律，讨论中间浪形缺陷的控制方法，常规板形控制手段不在此讨论。

第一，比较图4、图5中backup2和backup3型支撑辊接触应力及钢板凸度可以发现，将支撑辊主倒角长度从370 mm缩短至220 mm时，支撑辊变化引起的板凸度变化减小，且应力峰值低于原设计水平，即在保证支撑辊应力峰值降低的前提下，能够有效改善板形质量。在实际生产中，采用backup3型倒角后，钢板因中间浪形导致的矫直率从8%降低至2.5%以下。

第二，根据式（3），道次压下率与支撑辊倒角变化引起的道次比例凸度变化成正比，因此减小道次变形量可以控制板形。图6为实际生产规格为12 mm×1 700 mm×13 000 mm的钢板时分别采用8、10、12个道次轧制后的板形。随着轧制道次数的增加，末道次压下率逐步减小至8道次轧制时的40%左右，根据式（3）可知支撑辊倒角变化引起的道次比例凸度变化也减小至40%左右，钢板板形明显改善。8、10、12道次轧制的钢板凸度C150实测值分别为106、91、80 μm，根据式（1）计算的C150分别为20、0、－8 μm，不同轧制工艺条件下板凸度C150差值的计算结果与实际测量值较为接近，也在一定程度上验证了回归方程的有效性。考虑到增加轧制道次后钢板凸度会因轧制力降低而减小，因此在采取该措施时应保证钢板凸度不为负值。

图6 轧制道次数对板形的影响Fig.6 Effect of rolling passes on plate flatness

第三，该产线实际生产中工作辊沿辊身方向的磨损量不一致，辊身中段约1 500 mm区域磨损量大而越靠近边部磨损量小，形成一个带有一定凸度的工作辊辊形。当钢板宽度大于1 500 mm时，钢板凸度随着轧辊磨损的加剧和钢板宽度的增加而增大，这与支撑辊倒角对板凸度的影响规律相近，效果相反，可以抵消支撑辊倒角变化引起的板凸度及板形变化。图7为采用backup3型支撑辊后分别在轧辊中段磨损量为80与120 μm条件下生产规格为10 mm×2 100 mm×11 000 mm的钢板板形。经计算，当轧辊中段磨损深度增加40 μm 后，此宽度钢板凸度C150增加10 ～20 μm，根据式（1）计算可知backup3型支撑辊倒角变化引起的C150变化约－20 μm，两者叠加后C150值与使用backup1型支撑辊时基本一致，板形良好。基于这一思路，可以适当调整轧制计划，将宽板的轧制顺序后延，利用轧辊磨损后的辊型来改善板形。