一种高精度的儿童成年身高预测方法

(1.浙江工业大学 计算机科学与技术学院，浙江 杭州 310023；2.浙江大学医学院附属浙江医院，浙江 杭州 310023)

近年来，儿童青少年生长发育问题受到广泛关注。国务院在2017年发布的《国民营养计划》中明确指出：到2020年，中国儿童青少年的生长迟缓率要保持在5%以下[1]。在我国，针对儿童成年身高预测的研究主要应用在运动员的选材方面[2]。在运动员选材时，身高是一项十分重要的形态指标。有些项目需要运动员个子高一些，如篮球、排球等；有些项目需要运动员个子矮一些，如举重、跳水等。这就需要教练员在选拔运动员之前能够准确预测他们成年后的身高[3]。儿童青少年在生长发育过程中可能会因为某些激素的缺失影响身高的增长，如生长激素的缺失会导致儿童身材矮小，无法达到同龄人的标准身高[4]。对儿童青少年成年后身高的预测，不但能够及时发现儿童青少年在生长发育过程中的异常情况，而且还能及时进行干预治疗，帮助其减少发育异常带来的不良影响。儿童青少年的成年身高作为评估其生长发育情况的一项重要指标，一直是大家关心的重点[5]。因此，提出一种较为精确的身高预测方法具有重要的社会意义。目前，国内外的专家学者提出了很多儿童成年身高预测方法：贺矗[6]提出了一种利用赤足迹来预测身高的方法，根据主成分分析法从赤足迹中得到主成分，利用这些主成分构建的多元回归模型虽然比当前已有的多元回归方程准确度更高，但是该方法实验时所使用的样本量较少，实验结果的适用性还有待进一步验证；潘嘉严等[7]对TW2法中的身高预测公式进行了改进，得到了TW3成年身高预测改良法，与传统的身高预测方法相比，准确度得到了提高；Karlberg等[8]利用父母身高、儿童的妊娠长度、出生时的大小、最高峰速度的估计年龄(PHV)和8岁之前的身高测量值，结合多元回归分析，预测儿童青少年的成年身高；Beunen等[9]使用Beunen-Malina-Freitas方法来预测女孩的成年身高，该方法虽然在预测12～15 岁女孩的成年身高时是有效的，但是在预测较低年龄段女孩成年身高时准确度较低。后面两个方法所使用的实验数据并非来自中国，并且年代久远，因此不太适用于中国人口或具有中国血统的人口。随着人工智能领域的兴起，机器学习的方法在儿童青少年身高预测上被广泛应用：Shmoish等[10]根据儿童青少年的身高和体重数据，分析了线性、多层感知机(MLP)、决策树和随机森林等回归模型预测儿童成年身高的可行性，发现随机森林回归模型预测精度较好；Thodberg等[11]提出了一种基于骨龄自动评判的成人身高预测新方法，并取得了不错的结果。

虽然目前已有大量的身高预测方法，但是大多数方法都已经随着儿童青少年身体素质的提升而被逐渐淘汰，并且预测的准确率也不够高。为了准确预测儿童青少年的成年身高，笔者基于BP神经网络提出一种高精度的儿童成年身高预测方法。针对BP神经网络易陷入局部最优解的不足，提出一种基于位置策略的蚁狮算法(Location strategy ant lion optimization，LSALO)并对其进行优化。该算法的主要改进之处在于改变了蚂蚁随机游走的方式，加强了算法的全局搜索能力。

1 BP神经网络预测模型

BP神经网络是一种按误差反向传播算法进行学习的多层前馈网络，由输入层、隐藏层和输出层构成，是目前应用最广泛的神经网络模型之一[12]。典型的BP神经网络如图1所示，图1中(X1，X2，…，Xn)为一组输入值，其期望值为Y；Wij为输入层与隐藏层之间的权值；i为输入值的个数；j为隐藏层神经元的个数；Vj1为隐藏层与输出层之间的权值。BP神经网络预测模型主要由两个过程构成：输入信号的正向传播和误差信号的反向传播。正向传播时，传播方向由输入层经过隐藏层最后从输出层输出，若在输出层得到的值与期望值相差较大，则开始误差信号的反向传播，按误差梯度下降的方式修正各层权值[13]。通过这两个过程对网络进行反复训练，最终使输出结果的误差在要求的范围内。

图1 BP神经网络示意图Fig.1 Schematic diagram of BP neural network

2 ALO算法

蚁狮优化算法ALO (Ant lion optimizer)是澳大利亚学者Mirjalili[14]在2015年提出的一种新的群体智能优化算法。研究证明：蚁狮算法的寻优能力要优于粒子群算法、遗传算法和萤火虫算法等7 种智能算法，该算法通过模拟自然界中蚁狮捕捉蚂蚁的行为进行全局最优解的搜索[14]。蚁狮算法包括以下几个角色：蚂蚁、蚁狮以及精英蚁狮。蚂蚁代表尝试解，它可以围绕蚁狮随机游走，尝试寻找解空间上的最优解；蚁狮代表局部最优解，当围绕蚁狮游走的蚂蚁搜索到比该蚁狮更优的位置时，蚁狮会将蚂蚁“吃掉”(将蚂蚁当前位置赋值给蚁狮)，取代蚂蚁当前的位置；精英蚁狮代表全局最优解，每次更新后，都会从全部蚁狮中选取位置最好的蚁狮作为精英蚁狮。通过这样不断迭代，最后得到一个较精确的全局最优解。

蚂蚁的随机游走可以通过数学的方式表示为

X(t)=[0,cumsum(2r(1)-1),cumsum(2r(t)-
1),…,cumsum(2r(T)-1)]

(1)

式中：cumsum为位置的累加和；t为当前的迭代次数；T为最大迭代次数；r(t)为一个随机函数，表示为

(2)

式中rand为在[0,1]的范围内生成的随机数。蚂蚁的游走范围并不是无限制的，蚂蚁只能在搜索空间内发生随机游走的动作，具体公式为

(3)

(4)

(5)

式中：ct为所有变量在第t次迭代时的最小值；dt为所有变量在第t次迭代时的最大值。

通过适应度函数可以判断蚂蚁位置的优劣，并记录每个蚂蚁的适应度值，即

(6)

式中：FOA用来记录每组蚂蚁的适应度；Ki,j为第i个蚂蚁第j维的值；n为蚂蚁的数量；f为适应度函数。

适应度越高，说明蚂蚁的位置越好。在每一次迭代时，如果在蚁狮的狩猎范围内出现适应度更高的蚂蚁，蚁狮就会将其捕捉并吃掉，代替蚂蚁原来的位置，即将蚂蚁的位置值赋值给蚁狮，表达式为

(7)

每次迭代之后，从所有蚁狮中选出一只适应度最高的蚁狮作为精英蚁狮。当迭代次数达到最大迭代次数或者误差范围时停止搜索，这时的精英蚁狮即代表解空间范围内的全局最优解。

3 LSALO-BP算法

蚁狮算法具有调节参数少、收敛精度高和鲁棒性好等优点，已被应用到多种参数寻优场合。在传统的蚁狮算法中，蚁狮位置的优劣是根据适应度来评判的，适应度高的蚁狮周围有更多的蚂蚁围绕其游走，找到解空间上全局最优解的概率增大。适应度低的蚁狮很少会有蚂蚁在其身边游走，蚁狮作用减小，同时可能会因为蚁狮的位置不佳，算法在一定程度上存在陷入局部最优的问题。因此，为进一步提高蚁狮算法的寻优能力，对算法进行改进。

3.1 蚁狮替换

在原始的蚁狮算法中，蚂蚁围绕蚁狮进行随机游走，蚁狮的选择使用轮盘赌的方式，对于适应度高的蚁狮来说被选中的概率更大。当蚁狮所处的位置不够好时，蚂蚁的寻优过程就相当于在局部范围内寻找局部最优解。为了降低这种情况发生的概率，在每次迭代时对蚁狮进行以下替换操作：

Step1假设原始的蚁狮数量为n，在一次迭代完成之后，随机初始化相同数量的蚁狮。

Step2计算新蚁狮群的适应度值，对原蚁狮群和新蚁狮群进行排序，适应度值较高的蚁狮排在前面。

Step3运用贪心选择机制选择适应度更高的n个蚁狮作为下一次迭代的原始蚁狮群。

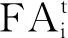
(8)

(9)

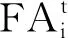
经过替换，原来位置不好的蚁狮被位置更好的蚁狮所替换。不仅蚂蚁在寻找最优解，蚁狮也同样在寻找最优解出现的范围。因此，算法的搜索能力得到了提高。

3.2 改进蚂蚁游走方式

每个新替换蚁狮适应度较高，但是会出现未被轮盘赌选中的情况，导致蚁狮替换成为无意义动作，无法发挥其作用。因此，只要判断出有新蚁狮的更替，就使蚂蚁围绕其随机游走，保证每个新蚁狮都有其存在的意义。而精英蚁狮是每次迭代后选出的全局最优解，它在很大程度上影响了蚂蚁的随机游走，所以在每次迭代时，让蚂蚁围绕精英蚁狮、新替换蚁狮以及通过轮盘赌选中的蚁狮进行随机游走。在蚁狮优化算法中，前期蚂蚁游走的步长要大，越到后期步长越小，直到收敛到某一位置附近，所以引入了步长调节函数y(t)，其数学表达式为

(10)

对蚂蚁随机游走的过程进行调整，数学表达式为

(11)

(12)

(13)

图2 y(t)函数图像Fig.2 Function image of y(t)

每次迭代蚂蚁随机游走的最终位置为

(14)

3.3 蚂蚁替换

假设有m个蚁狮被替换，蚂蚁寻优过程结束后就会出现m个新的蚂蚁。这些蚂蚁根据式(14)得到最终位置。蚂蚁的位置越好，适应度值越高，则越容易被蚁狮“吃掉”。因此，蚂蚁的位置在一定程度上决定了最优解出现的位置。为了提高LSALO算法的寻优效率，对适应度值低的蚂蚁进行替换。

(15)

(16)

蚂蚁替换过程和蚁狮替换过程是相辅相成的。蚁狮确定蚂蚁的搜索范围，蚂蚁在该范围内寻找最优解。在原始的蚁狮算法中，蚁狮的更替只能通过“吃掉”位置更好的蚂蚁来实现。算法改进后，位置较差蚂蚁和蚁狮能够被位置更好的蚂蚁和蚁狮替换，使得算法更容易找到最优解，提高了算法的搜索效率。

3.4 适应度函数选择

为了得到BP神经网络的最优权值，选择样本集实际值与BP神经网络预测值的均方误差作为预测准确度的判断标准。均方误差越小，说明当前的权值越好。因此，选择均方误差的倒数作为LSALO的适应度函数，其表达式为

(17)

式中：FMSE为均方误差；n为样本总数；Yi为第i个样本实际值；_Yi为第i个BP神经网络预测值。

3.5 LSALO-BP算法实施步骤

LSALO-BP算法由两个部分组成，LSALO部分和BP神经网络训练部分，具体步骤如下：

Step1初始化算法的各项参数。

Step2计算每个蚁狮所在位置的适应度值，记录每个蚁狮当前适应度值和全局最优值。

Step3记录每个蚁狮当前适应度值和全局最优值，将全局最优值作为权值赋值给BP神经网络，运行BP神经网络进行一次训练。

Step4根据BP神经网络的返回值，判断是否满足停止迭代条件，若满足，结束循环，否则跳至下一步。

Step5利用式(8，9)替换适应度值较低的蚁狮，并利用贪婪选择机制选择蚁狮。

Step6蚂蚁根据式(14)进行随机游走并更新其位置和适应度值。

Step7利用式(15，16)替换适应度值低的蚂蚁。跳转至Step 3。

LSALO-BP算法流程图如图3所示，其中左侧为LSALO部分，右侧为BP神经网络训练部分。

图3 LSALO-BP算法流程图Fig.3 LSALO-BP algorithm flow chart

4 实验结果与分析

4.1 数据采集及分析

本研究使用的数据集来自浙江省的中小学。笔者获取到儿童的基本信息，并通过回访的形式确认检测者成年后的身高，总计1 096 人，其中男生647 人，女生449 人。训练集和测试集的划分见表1。最终的数据信息包括：性别、年龄、骨龄和当前身高。这些数据来自浙江省的城市学校以及乡村学校，保证了数据的多样性，并且数据的可用性要优于来自医院的数据。

表1 训练集和测试集的划分Table 1 The division of training set and test set 单位：人

通过对回访样本数据的整理分析，样本中年龄人数的基本分布情况如图4，5所示。以6岁为例，表示的是6岁0～12月的人数。采集的数据样本中，男女生样本分布较均匀。处于青春期的人数较多，说明儿童在到达青春期后开始重视自身的身高情况。通过对比图4，5可知女生开始发育的时间要早于男生。

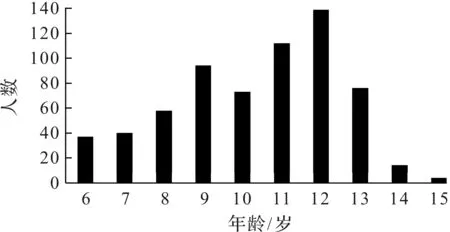
图4 男生年龄人数分布情况Fig.4 Distribution of boys by age

图5 女生年龄人数分布情况Fig.5 Distribution of girls by age

样本中骨龄的分布情况如图6，7所示。根据骨龄和年龄之间的关系，可将儿童的发育情况分为3 种，即发育迟缓、发育正常和发育提前。发育迟缓表示骨龄小于年龄1 岁或1 岁以上，发育正常表示骨龄和年龄相差在1 岁以内，发育提前表示骨龄大于年龄1 岁或1 岁以上。样本中包括了以上3 种发育情况的儿童，具有可靠性。

图6 男生骨龄人数分布情况Fig.6 Distribution of boys’ bone age

图7 女生骨龄人数分布情况Fig.7 Distribution of girls’ bone age

4.2 基准函数测试结果

为了验证位置策略的有效性，选取10 个基准函数进行算法的对比实验，结果如表2所示。表2中：f1～f4为单峰函数；f5～f7为多峰函数；f8～f10为固定低纬度下的多峰函数。对比的对象为原始ALO算法以及文献[15]提出的OB-L-ALO算法[15]。

表2 基准函数Table 2 Benchmark function

为了体现本次对比实验的公平性，3 种算法采用相同的参数设置，即种群规模N=30，最大的迭代次数T=1 000，并且将不同算法对每个基准函数独立运行30 次，取实验结果的平均值进行比较，以减小随机性带来的影响。ALO算法、OB-L-ALO算法和LSALO算法的实验结果如表3所示，ALO算法和LSALO算法的迭代收敛曲线对比情况如图8所示。

表3 基准函数对比情况Table 3 Benchmark function comparison

表3 (续)

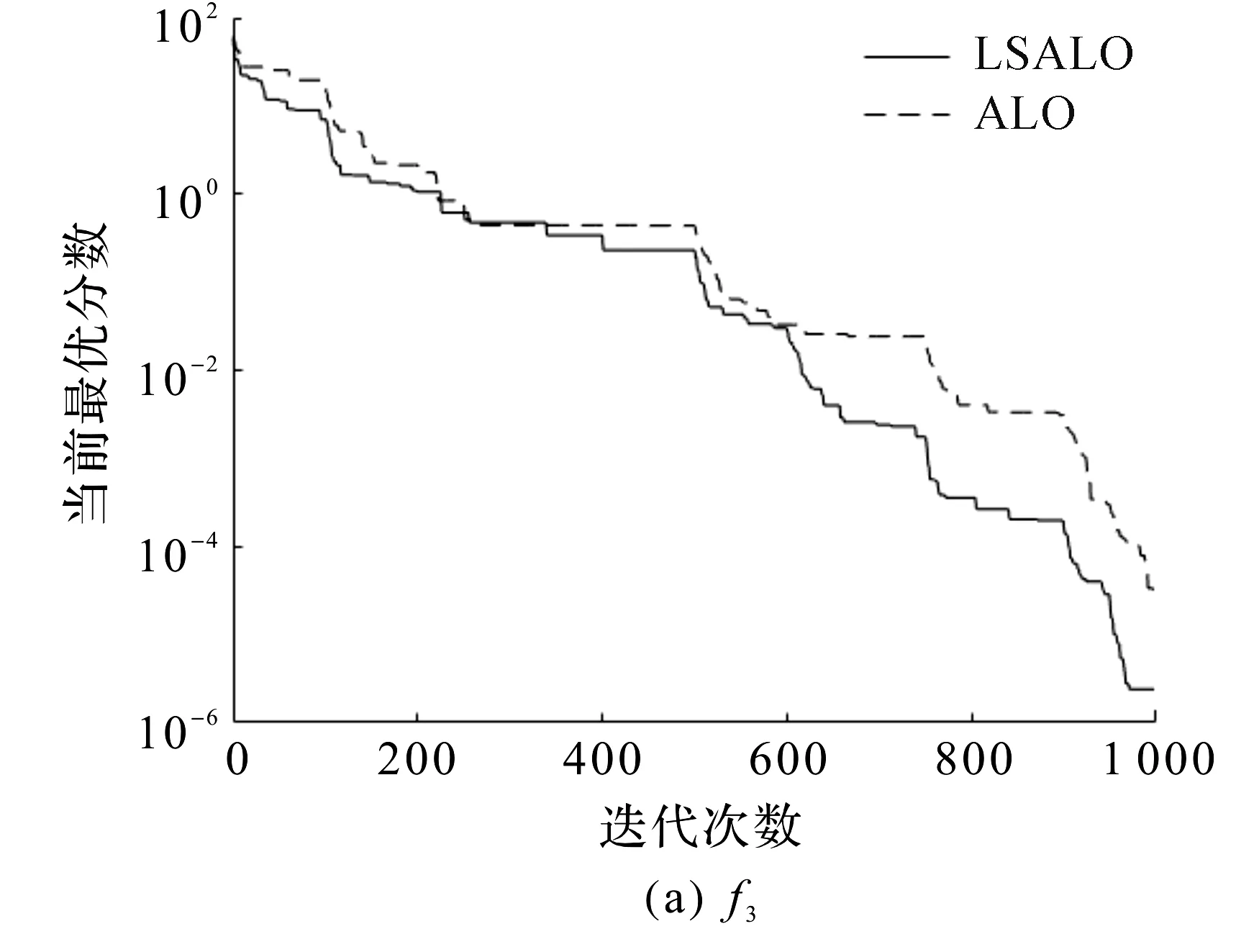
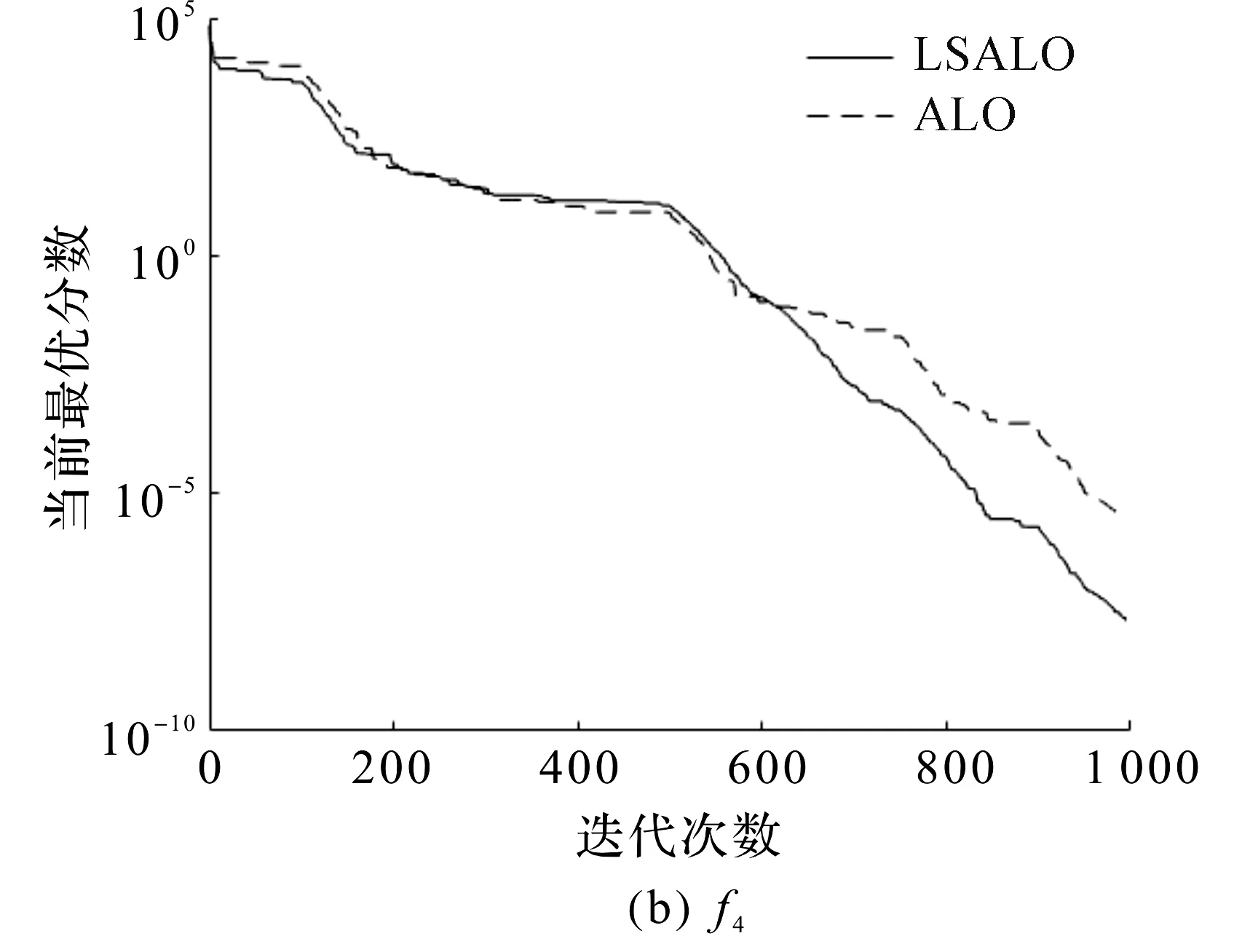
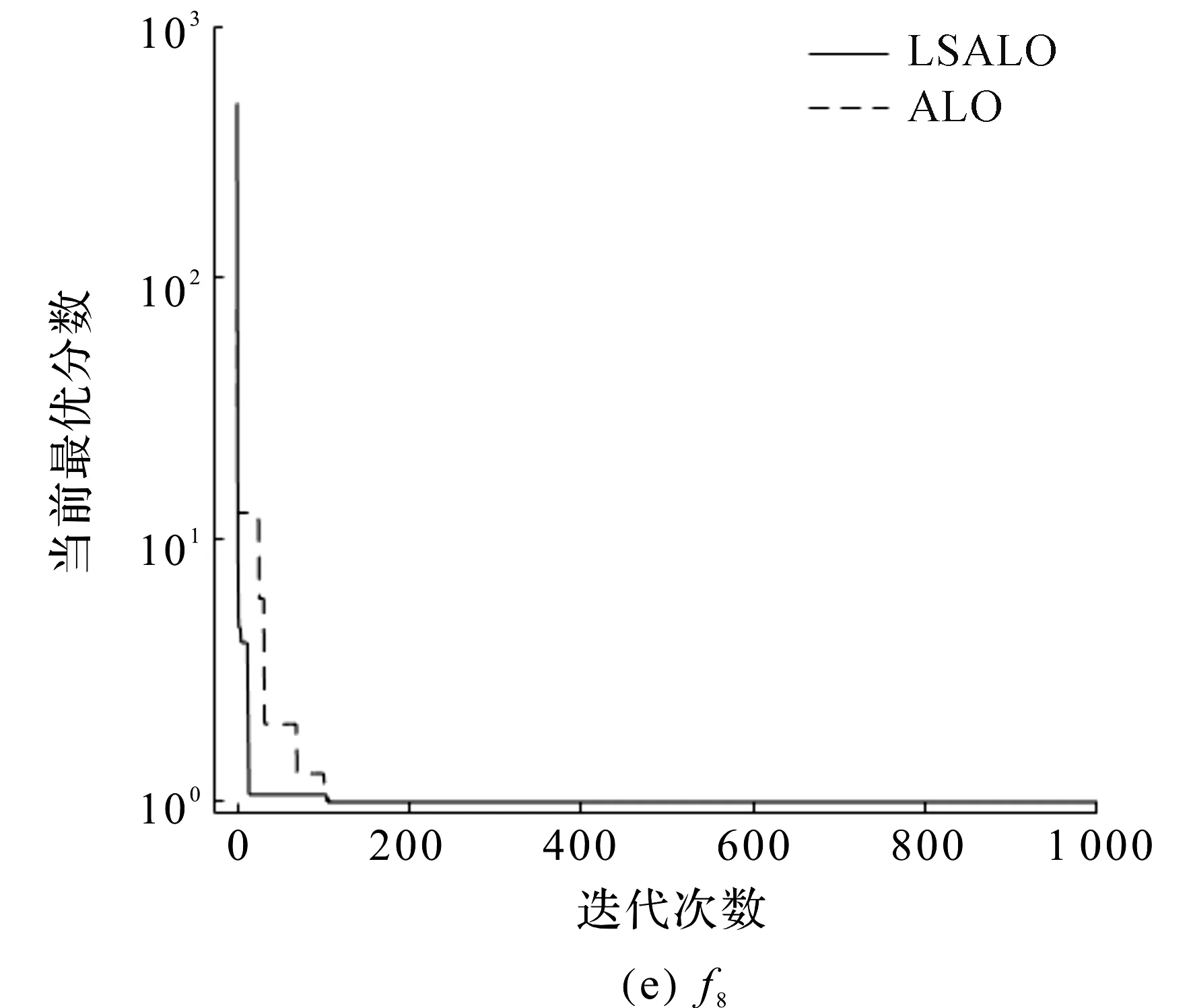
图8 基准函数的迭代曲线Fig.8 Iteration curve of benchmark function

由表3和图8可知：与其他算法相比，LSALO算法取得了更好的实验结果。对于单峰函数f3和f4，LSALO算法的实验平均结果相比ALO算法和OB-L-ALO算法提高了1～5 个数量级，且标准方差更小，说明该算法的寻优能力强，稳定性好。对比函数f3和f4的收敛曲线发现，LSALO算法的收敛精度更高。对于多峰函数f5，ALO算法在迭代次数不到100 次时就陷入了局部最优，导致算法寻优过程早早结束。而LSALO算法的位置策略使得该算法不易陷入局部最优，全局搜索能力更强。对于固定低纬度下的多峰函数f8和f9，LSALO算法的结果平均值已经达到了理论上的最优值，寻优率达到了100%。

综上所述，根据基准函数的优化结果可知：LSALO在全局寻优能力和收敛精度方面均优于ALO算法和OB-L-ALO算法，说明该算法是有效可行的，可以进一步应用于BP神经网络的权值寻优问题，改进后的BP网络可用来预测儿童成年身高。

4.3 实验结果

4.3.1 BP网络结构

BP神经网络输入变量选取准则有两点[16]：1) 输入变量应与预测对象密切相关；2) 输入变量之间不能有较强的线性关系。基于这两个准则，选取儿童检测时的身高、骨龄以及年龄作为输入量，表达式为

Xi=(X(age)i,X(boneage)i,X(height)i)

(18)

式中：Xi为第i组输入值；X(age)i为第i个儿童的检测年龄；X(boneage)i为第i个儿童当前的评估骨龄；X(height)i为第i个儿童的当前身高。输出层以儿童成年预测身高作为输出值。

骨龄、年龄等身体基本信息和成年身高之间并不是简单的线性关系，且每个儿童的生长发育情况不同，导致输入量呈现多样性的特征。BP神经网络具有较强的非线性映射能力和自学习能力，能够更高效地建立多因子模型[17]，本次实验的BP神经网络采用双隐藏层的设计。

在BP神经网络模型中，隐藏层节点数太少将导致欠拟合，节点数过多将导致过拟合，降低神经网络的泛化能力。常用的隐藏层节点数选择公式为

(19)

式中：NH为隐藏层节点数；ni为输入层节点数；l为输出层节点数；∂为1～10的常数。根据式(19)计算，隐藏层节点数NH的取值范围可以确定为[2,12]。大量实验表明：当第1层隐藏层节点数为输入层节点数的2倍，第2层隐藏层节点数和输入层节点数一致时，BP神经网络的训练效果最好。因此，可以确定BP神经网络的结构为3-6-3-1。

4.3.2 预测结果比较

将LSALO-BP模型与GA-BP模型[18]、PSO-BP模型[19]、BP神经网络和Bayley-Pinneau法[20]进行对比，对样本进行预测分析。以真实值和预测值的差值是否在±2 cm以内作为准确性的判断依据。男生、女生成年身高预测的分析结果分别如表4，5所示。由表4可知：LSALO-BP模型针对男生的预测结果在准确性和标准差方面要优于其他预测模型，准确率达到了86.67%，标准差为1.176，相较于BP神经网络，准确率提高了16.08%；由表5可知：LSALO-BP模型针对女生的预测结果在准确性和标准差方面仍然优于其他预测模型，准确率达到了85.32%，标准差为1.615。

表4 男生成年身高预测分析Table 4 Predictive analysis of adult height of boys

表5 女生成年身高预测分析Table 5 Predictive analysis of adult height of girls

误差分析结果采用箱线图展示，结果如图9所示。箱线图能够直观地判断误差的离散分布情况，了解误差的分布状态，并能识别出误差中异常值。误差的范围用垂直距离表示，误差的四分位间距由箱子的高度表示。图9(a，b)分别表示男生、女生的误差分析结果。由图9(a)可知：LSALO-BP模型预测误差的四分位间距和中位数都要优于其他预测模型；由图9(b)可知：LSALO-BP模型预测误差的四分位间距和中位数与Bayley-Pinneau法相似，但是异常值的数量要少于Bayley-Pinneau法。综合以上分析可知LSALO-BP预测模型的性能要优于其他预测模型。

图9 误差分布图Fig.9 Error distribution map

笔者利用回访的儿童青少年成年身高样本，对基于LSALO-BP模型的儿童青少年成年身高预测模型进行实例验证，每个性别随机抽取20 个实例，预测结果如表6，7所示，其中年龄、骨龄以及身高指的是当时检测时所采集的数据，成年身高是回访采集到的数据，绝对差值表示成年身高和成年预测身高之间差值的绝对值。由表6可知：男生的成年身高与成年预测身高的绝对差值总体保持在±2.0 cm范围内，最大差值为2.68 cm，最小差值为0.02 cm；由表7可知：女生的成年身高与成年预测身高的绝对差值总体也都保持在±2.0 cm 范围内，最大差值为2.42 cm，最小差值为0.02 cm。实例验证表明：基于LSALO-BP模型的儿童青少年成年身高预测模型预测结果精确度较高，误差波动较小，可以用来预测儿童青少年成年身高。

表6 男生成年身高预测具体结果Table 6 Prediction results of adult height of boys

表7 女生成年身高预测具体结果Table 7 Prediction results of adult height of girls

5 结 论

针对传统成年身高预测存在预测方法过时、预测精度不高等问题，基于BP神经网络提出了一种高精度的儿童成年身高预测方法。为了弥补BP神经网络易陷入局部最优解的不足，提出基于位置策略的蚁狮优化算法。该算法通过改变蚂蚁的游走方式和替换方式，增强了全局搜索能力和局部优化能力。通过对不同基准函数的优化求解，将LSALO与原始蚁狮算法和其改进算法进行对比，验证了位置策略的有效性。将LSALO算法优化的BP神经网络应用于儿童成年身高预测，选取4 种不同的模型与其进行对比。实验结果表明：LSALO-BP模型的预测精确度更高，误差波动更小，可以准确地预测儿童成年身高。