智能车辆转向姿态鲁棒滚动时域估计
2022-01-26
(浙江工业大学 信息工程学院,浙江 杭州 310023)
随着电子安全技术的发展,主动安全系统如电子稳定控制系统(Electronic stability control system, ESC)和防抱死制动系统(Anti-lock brake system, ABS)在危及安全的情况下发挥着越来越重要的作用。例如,2015年ESC在美国挽救了1 949 人的生命,但仍有2 272 人死于各类车辆事故[1]。为了保证此类安全系统的最佳性能,获取的车辆姿态信息必须非常准确,航向角轻微的偏差将会导致车辆偏离原来的行驶路线;质心侧偏角是判断车辆是否稳定的关键依据;横摆角速度是车辆动力学控制系统进行控制决策的主要依据。现有的车辆姿态测量数据来源主要有传感器、陀螺仪和全球导航卫星定位系统[2-5]。然而,在测量过程中,车辆姿态的数据通常会受噪声的污染以及环境的影响,难以精确或者经济地测量车辆姿态,这就产生了对可靠的在线估计算法的需求。
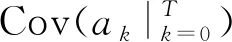
1 问题描述
智能车辆转向系统如图1所示。图1中XOY为惯性坐标系;a和b分别为车辆质心到前轴和后轴的距离;Fyf和Fyr分别为车辆前轮和后轮轮胎侧向力;δf为前轮转向角;v为车辆速度,vx为车辆纵向速度,vy为车辆横向速度;β为质心侧偏角;r为横摆角速度。
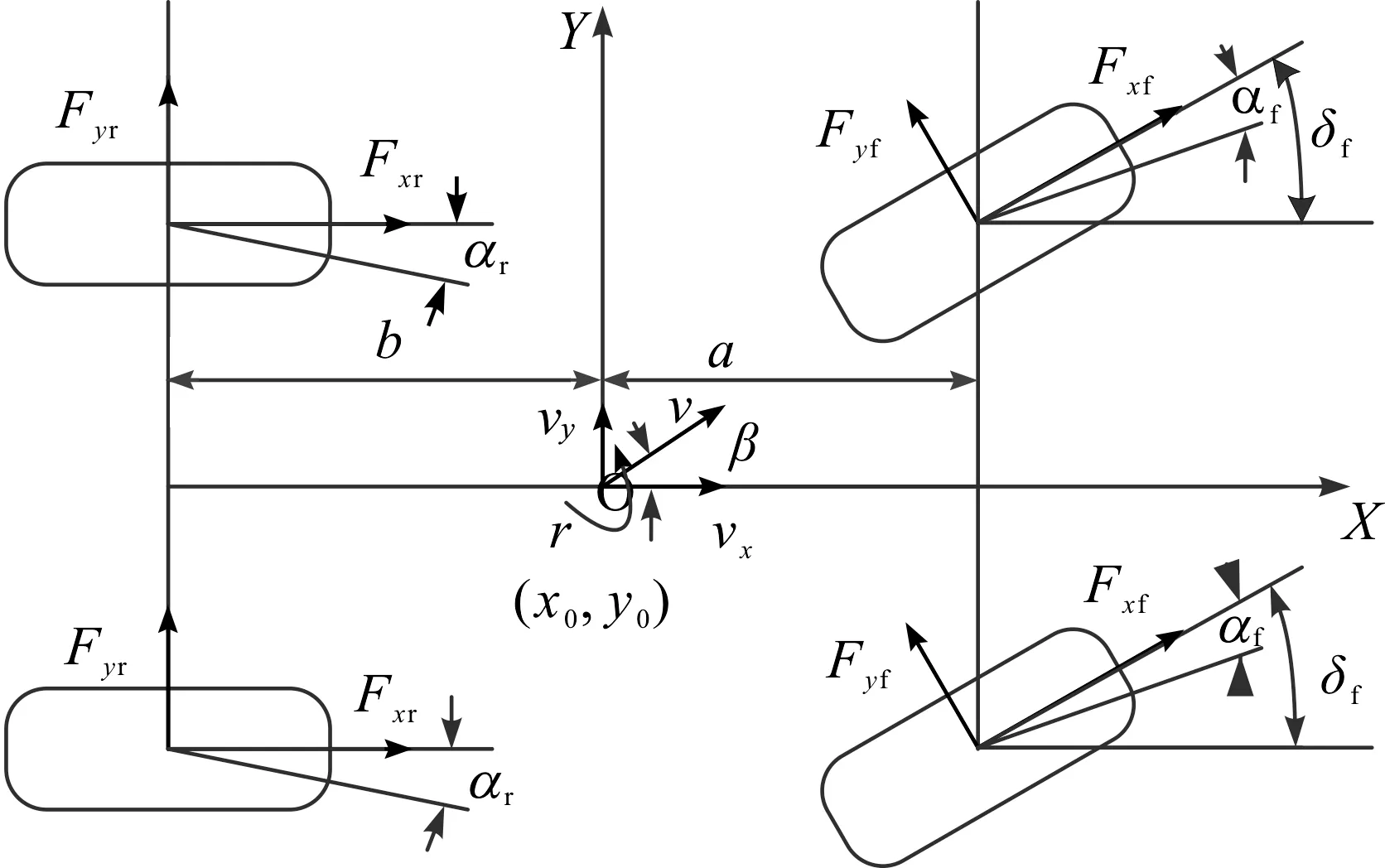
图1 车辆转向系统模型Fig.1 The model of vehicle steering system
在车辆动力学建模中,为简化模型,通常忽略空气动力学和悬架俯仰运动的影响,假设纵向速度在短时间内保持不变,忽略纵向动力学,则二自由度动力学模型的数学表达式为

(1)
式中:m为车辆质量;Iz为车辆绕z轴的转动惯量;Cf和Cr分别为车辆前轮和后轮侧偏刚度。在车辆侧向轮胎力未达到饱和状态时,前、后轮侧向力与轮胎侧偏角基本呈线形关系,其表达式分别为
(2)
在运动学建模中,假设车辆为刚体。车辆纵向位置x0、侧向位置y0和横摆角φ可分别表示为
(3)
基于小角度θ假设(θ表示每个角度,包括前轮偏转角和前后轮胎侧偏转角),其满足近似条件cosθ≈1,sinθ≈θ。则质心侧偏角β可近似为
车辆纵向位置x0和侧向位置y0可简化为
(4)
联合式(1,4),可得车辆转向系统模型为
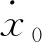
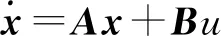
(5)
其中系数矩阵A和B分别为
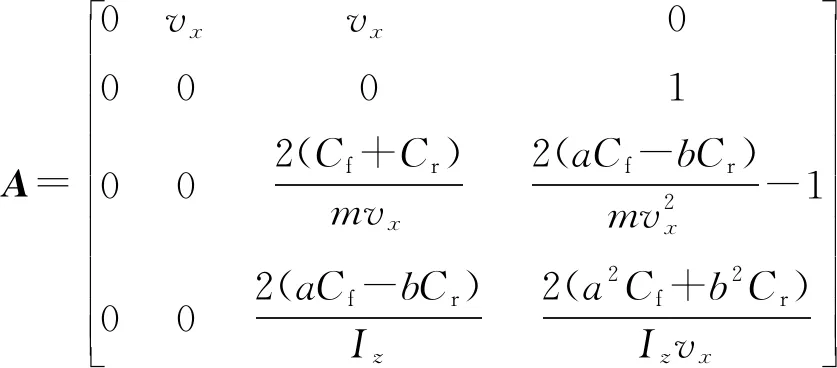
为获取车辆姿态信息需对车辆状态进行采样测量。以Ts为采样周期,将式(5)离散化得
x(T+1)=Acx(T)+Bcδf(T)+w(T)
(6)
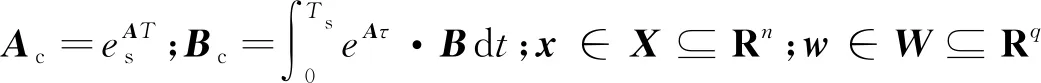
y(T)=Cx(T)+v(T)
(7)
式中:y∈Rp为T时刻收集到的车辆数据;C为已知观测矩阵,(C,Ac)可观;v∈V⊆Rp为T时刻接收到的车辆数据中所带有的不确定噪声,满足vmin≤v≤vmax。
由于外界环境中不确定扰动的影响以及现有测量工具的局限性,车辆姿态信息通常难以精确地测量,或者无法经济地测量,如测量车辆质心侧偏角和外部扰动的传感器十分昂贵,且信号的可靠性问题也尚未完全解决,使得这些信息目前在实际车辆系统中很难通过传感器测量直接获得。GNSS定位系统虽然可输出航向角度信息,但其随机噪声大,且速度越低噪声越大。此外,卫星信号的传递经常因受到地形和地物的影响而发生信号错误,甚至出现信号丢失等问题,因此在实际使用时经常会出现GPS无法提供信息或者所提供的信息偏差较大的问题。陀螺仪用于测量横摆角速度,但存在几何尺寸大、强度差、容易掉电和噪声大等问题。现在使用较多的微机械陀螺仪的几何尺寸虽然有所减小,噪声问题也有所改善,但还是存在着诸如标定误差和温度漂移等问题,其价格随性能的提高而增加,并且陀螺仪安装比较麻烦,要尽量安装在车辆质心位置,限制了它的广泛使用。
综合考虑硬件测量的精度、经济性和可操作性,设计观测器以减少对硬件的依赖非常必要。笔者基于噪声的不确定性,设计了鲁棒滚动时域估计,有效利用测量数据来估计车辆的姿态信息。
2 转向姿态鲁棒滚动时域估计
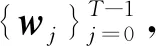
(8)
与经典滚动时域估计的目标函数不同,考虑数据测量以及传输过程中不确定噪声的影响,在目标函数中添加噪声抑制项来获得鲁棒性。参考H∞滤波的博弈近似理论[25,27],定义扰动抑制函数为
(9)
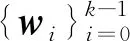
考虑数据传输时受不确定性噪声的影响,基于不确定离散线性模型式(6)的鲁棒全信息滚动时域估计问题(Robust full information estimation, RFIE)可表示为
(10)
s.t.xk+1=Acxk+Bcδfk+wk∈X
vk=yk-Cxk∈V
wk∈W,k∈I0∶T-1
(11)
其中目标函数为
(12)
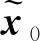
随着时间的推移,全信息滚动时域估计需处理更多的数据,为使估计问题可行并在计算上易于处理,引入固定时域N。当T>N时,优化问题RFIE的计算时域可分为{0≤k≤T-N-1}和{T-N≤k≤T}。则目标函数式(12)可改写为
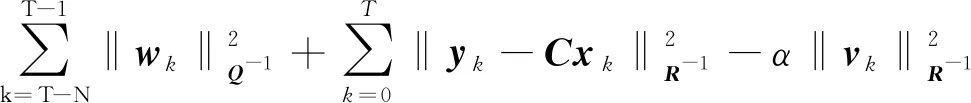
对任意可行初始状态x0和干扰序列{wk},定义T时刻系统状态可达集为
(13)
取s∈Sa,到达代价为
(14)
其中问题式(14)满足约束式(11)。
为适用于车辆快速转向,引入扰动块结构,在估计过程中,每个时刻均对估计窗口内的扰动进行分块,强制令同一扰动块结构内的扰动值相等,从而减少所求的优化变量,降低计算量。
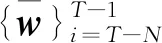
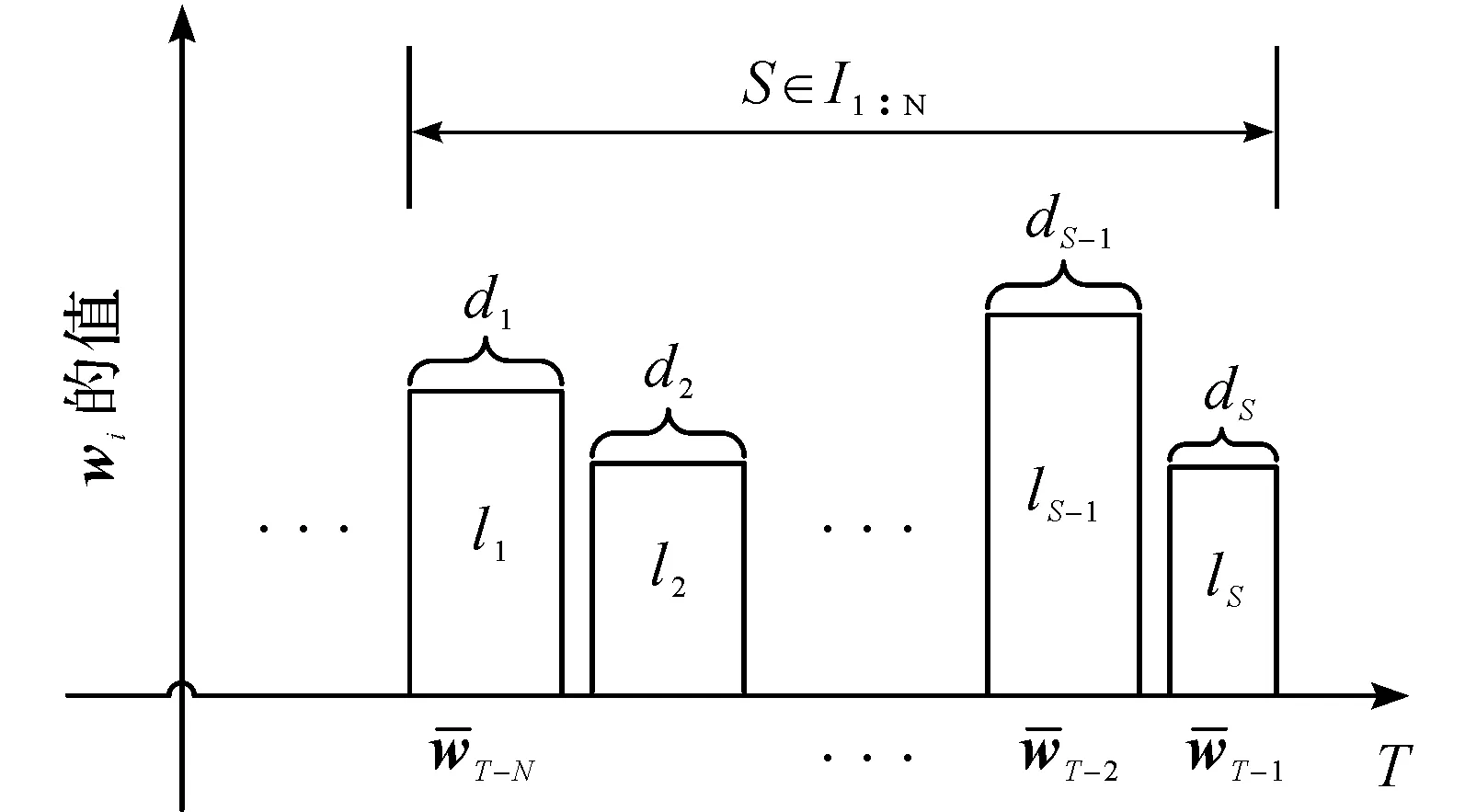
图的块结构示意图Fig.2 Segment structure of
给定估计时域N>n,在T时刻求解以下带有扰动块的鲁棒滚动时域估计问题(Blocking moving horizon estimation, BRMHE),即
(15)

(16)
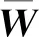
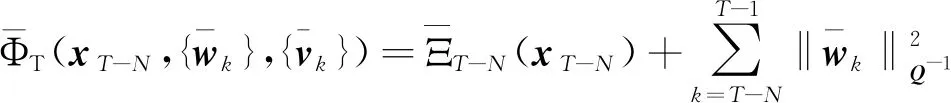
(17)
到达代价为
(18)
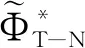
(19)
(20)
算法步骤:
1) (初始化):当T=0时,设定矩阵P0和车辆初始状态x0,其中P0为初始条件x0的协方差矩阵。
2) 当1≤T≤N时,求解优化问题RFIE。
3) 当T>N时,求解基于扰动块的鲁棒滚动时域估计问题BRMHE。
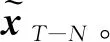
3 可行性与稳定性分析
针对RFIE问题可行性,为符号简便,式(12)记为
(21)
为证明算法可行性,需要以下引理来保证RFIE从x0估计x1的鞍点解的存在。
引理1[25]假设X,W,V为凸的紧集,ΦT在(x0,w0,v0)处连续。若对∀v0∈V,ΦT在点(x0,w0)处为凸;对∀x0∈X,w0∈W,ΦT在点v0处为凹,则函数ΦT存在鞍点。若函数ΦT为严格凹凸,则该鞍点是唯一的。
(22)
(23)
(24)
定义1[18]考虑线性系统,即
xk+1=Acxk+Bcδfk,yk=Cxk
(25)
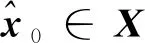

(26)
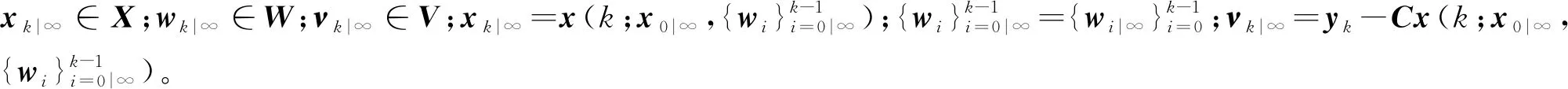
为书写清晰,令
(27)
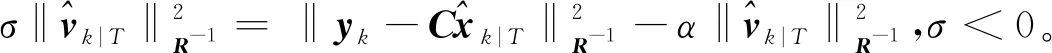

基于引理3,可获得如下结论:
定理1考虑车辆转向模型式(6),假设矩阵P0,Q,R正定,且假设1成立,则RFIE是渐近稳定的。
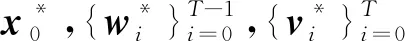
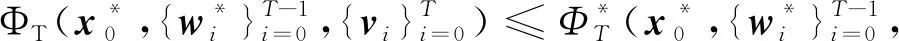
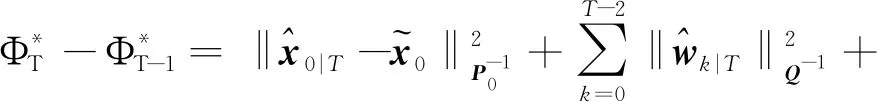
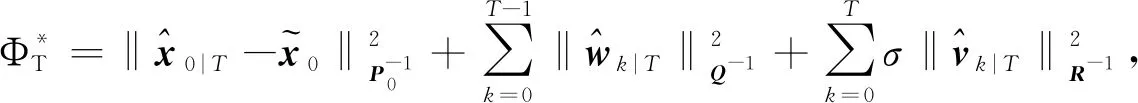
(28)
为证明稳定性,设ε>0,考虑T=n时,选择足够小的γ>0。若选择δ>0,使得ρδ2<γ,则对所有T≥n有
(29)
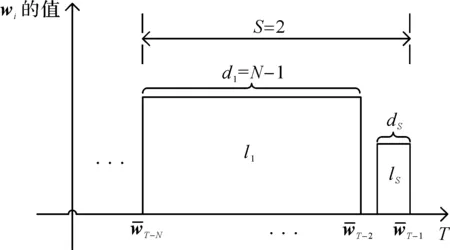
图3 S=2时的块结构示意图Fig.3 Segment structure of when S=2
最大分块长度块结构的扰动示意图如图3所示。式(15~18)特例可表示为
(30)

(31)
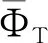
为符号简便,式(17)记为
(32)

通过定理2和定理3讨论BRMHE的可行性和引入扰动块结构后算法的估计性能。
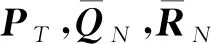
(33)
(34)
(35)
则式(15~18)在每个采样时间均存在唯一鞍点解,其中PT由式(20)给出。
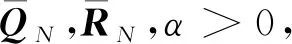
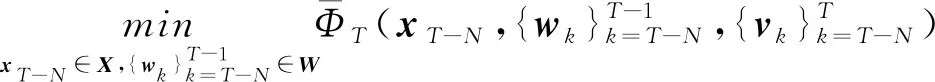
存在唯一解,即式(33,34)。
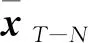
(36)
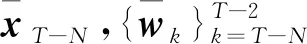
假设2系统矩阵Ac非奇异且满足
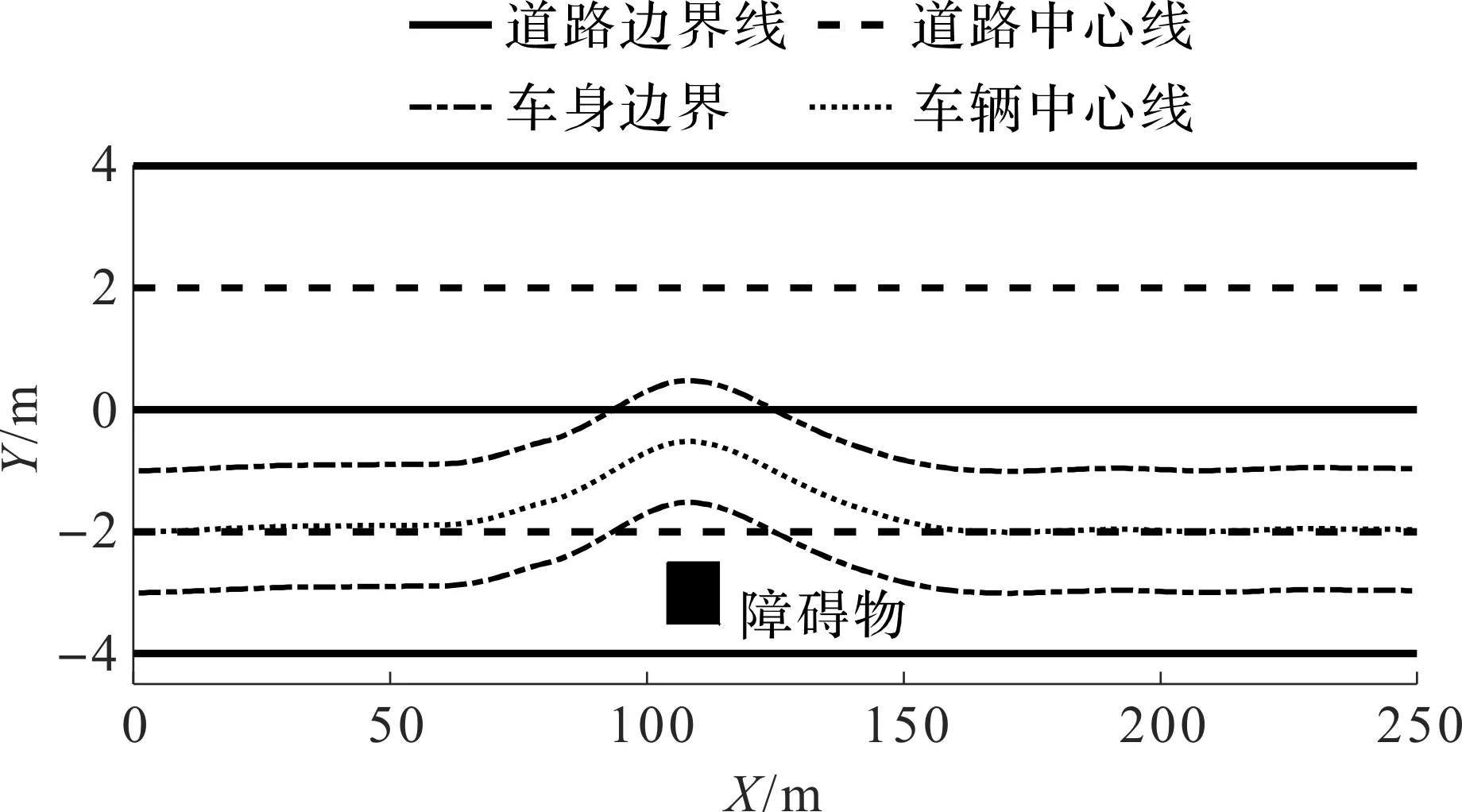
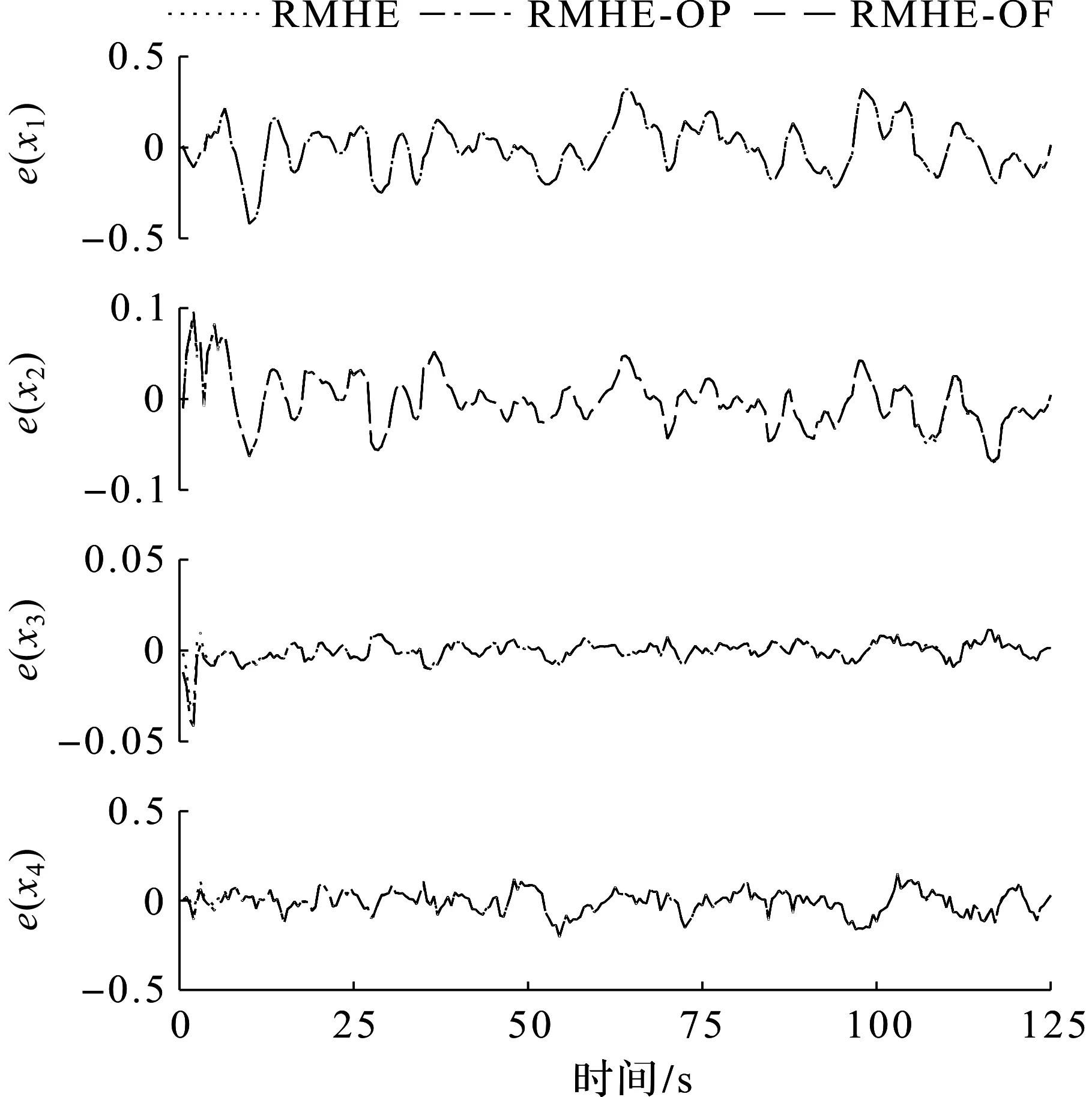
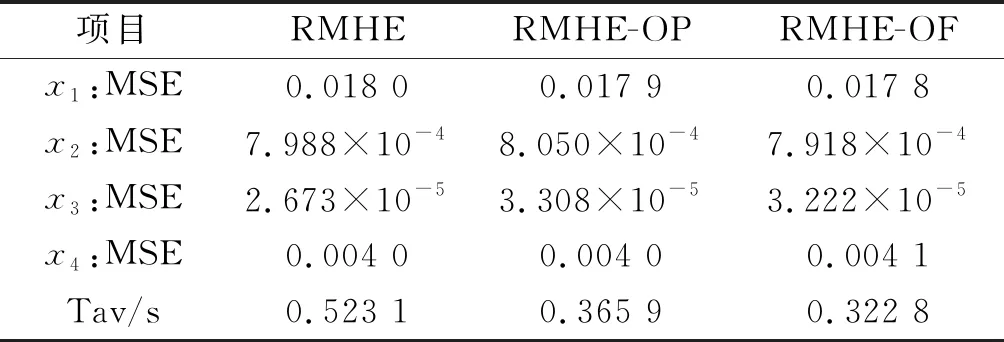
定理2若假设2成立,且S 满足 推论1若将窗口前N-1个扰动分为S块,BRMHE问题可行性和估计性能同样能得到保证。 证明由定理1可知,S=2时等价解存在,且S=2为S∈I3∶N的特殊情况,故当S∈I3∶N时至少存在一组等价解。其中S=N时,BRMHE等价于不设有块结构的RMHE。 基于推论1,若S=2时BRMHE收敛,则当S∈I3∶N时算法收敛性依然存在。故验证S=2时(最小分块数量)算法的收敛性。 为书写清晰,令 (37) 引理6考虑车辆转向模型式(6),则对任意s∈Rn,协方差矩阵PT满足 (38) 该引理证明过程与文献[28]引理4.4.4相似,此处省略。 定理3考虑网联车队模型式(6),若假设1,2成立,且N≥n,BRMHE估计器是渐近稳定的。 (39) 根据假设1,有 (40) 引理6可保证 (41) 联合式(40,41),则有 (42) 为证明稳定性,设ε>0,考虑T=N时,选择足够小的γ>0。若选择δ>0,使得ρδ2<γ,则对所有T≥N有 (43) 考虑到min-max问题具有较高的计算复杂度,因此引入坐标轮换法,分离min-max问题近似求解。min-max问题近似求解过程为 (44) 其中极小化问题满足约束式(11)。 (45) 其中优化问题满足约束式(11)。 若初始状态的置信度低,则可转至步骤2)进行多轮循环,直至连续两次循环求得的最优解的差小于给定收敛精度。鲁棒滚动时域估计最小-最大问题的近似解类似于鲁棒全信息滚动时域估计。 本节考虑在同向双车道上匀速运行的智能车辆,以评估所提算法的有效性。仿真中使用的自主车辆模型选取CarSim软件中的C级掀背式轿车模型,车辆模型中参数以及控制器参数如表1所示。 表1 车辆及控制器参数Table 1 Vehicle and controller parameters 设自主车辆纵向行驶速度vx=25 m/s,初始位置x0=0 m,y0=-2 m,在行驶过程中设置静态障碍,如图4所示。采用模型预测控制(Model predictive control, MPC)规划避障路径[29],假设该障碍物相邻车道有足够的横向空间,自主车辆经控制后,可从障碍物侧面安全避开。为准确获取车辆行驶过程中的状态,通过测量状态分量x1(车辆纵向位置)来估计状态。仿真满足假设1~4,设不确定扰动w∈[-0.1,0.1],不确定噪声v∈[-1,1],α,P0,Q,R满足式(33~35),分别为α=0.9,P0=diag[0.01,0.01,0.01,0.01],Q=diag[9×10-4,9×10-4,9×10-4,9×10-4],R=0.1。采样时间Ts=0.5 s,滚动窗口N=6,初始状态x0=[-2,0,0,0]。 图4 MPC规划路径Fig.4 MPC planning path 在仿真中分别对比了3 种不同块结构BRMHE算法:1) 标准RMHE算法(扰动不分块);2) 将扰动分别分为长度为d1=3,d2=2,d3=1的块结构,记为RMHE-OP;3) 将扰动以最大分块形式划分,即窗口内最后扰动单独分为1 块,其余扰动分为1 块,记为RMHE-OF。仿真结果如图5,6所示,图5,6分别为各算法估计状态轨迹图和估计误差图:实线表示实际状态轨迹;虚线、点划线和双划线分别表示RMHE,RMHE-OP和RMHE-OF的仿真结果。各算法的估计均方误差(MSE)和各算法所需的平均计算时间(Tav)如表2所示。仿真结果显示:3 种鲁棒分块算法的估计状态轨迹均收敛于实际轨迹,且均方误差相近,此外在块结构约束下,算法RMHE,RMHE-OP和RMHE-OF的优化变量分别为7,4,3 个。分析图6和表2可知:各算法的计算速度满足RMHE 图5 状态轨迹Fig.5 State trajectory 图6 各算法估计误差Fig.6 Estimation error of each algorithm 表2 各算法估计均方误差(MSE)和平均计算时间(Tav) 通过结合滚动时域估计算法与博弈论方法,设计可处理不确定噪声的鲁棒滚动时域估计器。采用坐标轮换法近似求解min-max优化问题。为降低算法复杂度,在鲁棒滚动时域估计算法中,通过设计扰动块结构以及构造等价解有效降低算法计算量,从而达到快速估计的目的。仿真结果表明:设计的鲁棒滚动时域估计算法能有效处理智能车辆转向系统中带有不确定噪声的姿态估计问题,具有较好的抗扰性,且鲁棒快速滚动时域估计算法中扰动分块数量越少,算法估计时间越短,对于满足可行性条件的不同分块形式的鲁棒滚动时域估计算法,均可在保证估计性能的基础上降低计算时间。笔者主要讨论车辆转向姿态模型中基于不确定扰动与测量噪声的估计,后续还可进一步考虑模型的结构和参数的不确定性问题。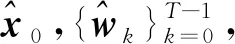
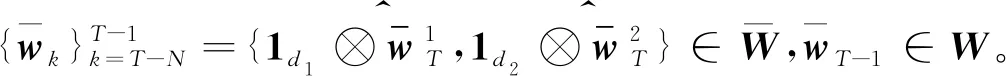


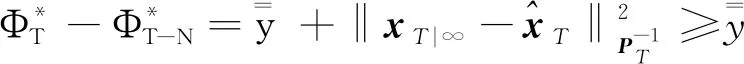


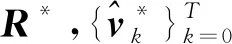
4 仿真与结果分析


5 结 论
