水下滑翔机纵垂面变浮力过程建模与控制优化

严 升 张润锋 杨绍琼，3 牛文栋，3 张宇航 李保玉

1.天津大学机构理论与装备设计教育部重点实验室，天津，3003502.天津大学青岛海洋技术研究院，青岛，2662373.青岛海洋科学与技术试点国家实验室海洋观测与探测联合实验室，青岛，266237

0 引言

水下滑翔机(underwater glider，UG)是一种依靠净浮力驱动的新型海洋观探测工具[1]。水下滑翔机通过特定阶段间歇性地改变自身净浮力实现垂直面内的上浮和下潜运动，同时依靠改变自身重心在垂直纵剖面的位置调整滑翔运动过程中的姿态，从而改变受到的水动力。通过净浮力与水动力的共同作用使得水下滑翔机在垂直剖面内实现锯齿状运动。由于水下滑翔机改变自身重力和重心是间歇性的且调节频率较低，因此能耗非常小，适合执行长时序、大范围的海洋环境监测任务。

为了对水下滑翔机进行运动控制优化，需要对其进行动力学建模与参数识别。目前，国内外学者对各型号水下滑翔机的动力学研究已取得显著的成果。普林斯顿大学的Leonard是水下滑翔机理论研究的重要先行者，其研究团队通过改变重块安放点来改变实验样机的重心位置，从而得到不同重心位置下相对应的滑翔轨迹，并且利用几何力学和动力学理论对实验样机的运动行为进行动力学分析[2-3]；王树新等[4]、王延辉[5]、孙秀军等[6]利用浮基多刚体理论和鱼雷水动力模型建立了水下滑翔机的动力学方程，并利用吉布斯-阿佩尔方程对非线性动力学方程的准确性做进一步优化；武建国[7]基于FLUENT软件计算了混合驱动水下滑翔机滑翔状态下机翼的水动力特性，给出了水下滑翔机不同运动状态下最大升阻比时对应的攻角，优化了水下滑翔机的航行效率；王旭超等[8]对水下滑翔机进行了运动学和动力学建模，并在此基础上设计了控制器，进行了俯仰和偏转过程的仿真研究。

较早的部分文献为了简化建模过程，将水下滑翔机的回排油动作视为油囊体积变化引起的浮力改变，且将这种变化用单独在外油囊处的作用力来体现。现在，主流文献将水下滑翔机可浸水舱部分的海水质量作为其自身质量的一部分，但是对水下滑翔机建模的影响考虑不充分，仅引入了浮力调节质量的概念，缺少对油液质量的转移过程的描述以及对可浸水舱部分海水质量的准确计算，进而导致建模过程中排回油行为表述不准确，并且随着深度的变化其海水密度和压强对浮力的影响也未反映到水下滑翔机的动力学模型中，导致现有水下滑翔机模型不能较好地反映真实的运动行为。目前水下滑翔机主要采用不依赖于模型的控制方法，如自适应控制、模糊控制以及神经网络等智能控制[9]。传统的控制方法比较简单且容易应用在工程实践中，但存在精度和能源利用率低等问题，而随后发展起来的控制方法虽然提高了控制精度，但是对水下滑翔机的适用性不强，且大部分仍处于实验和仿真阶段[10]。

本文以天津大学自主研制的“海燕-Ⅱ”混合驱动水下滑翔机作为研究对象进行动力学建模及运动仿真分析，并引入了不同深度海水密度与压强的变化参数，将水下滑翔机搭载的温盐深仪观测数据作为关键参数导入模型中，通过PID控制器调控的动力学模型进行数值仿真可以得到该型水下滑翔机电池包的前后移动量(以下简称“俯仰舵量”)与深度之间的关系。仿真得到的控制参数可作为水下滑翔机的直接控制参数，适合“海燕-Ⅱ”水下滑翔机的控制流程且可在能源利用率相同的条件下增强其运动性能。

1 海燕-Ⅱ水下滑翔机建模

1.1 水下滑翔机简化模型

在对水下滑翔机动力学建模过程中，可将其简化为由多个质点组成的系统[11]。水下滑翔机完全进入海水后，前后导流罩内会充满海水，这部分海水由于导流罩和天线杆的形状特点及进(排)水孔径的限制会时刻跟随水下滑翔机主体一起运动，因此，这部分海水质量可视为水下滑翔机自重的一部分。海燕-Ⅱ水下滑翔机的整体结构如图1所示。

图1 海燕-Ⅱ水下滑翔机Fig.1 Petrel-Ⅱ underwater glider

通过三维模型分析，可计算出海燕-Ⅱ水下滑翔机该部分海水总质量为9.95 kg，约占总体质量的1/9，该部分质量对水下滑翔机的运动有一定程度的影响，因此有必要考虑该部分质量，建立精确的水下滑翔机模型。

水下滑翔机回排油动作会引起外油囊的体积变化，同时将水下滑翔机前导流罩内的海水通过排水孔挤入或排出导流罩，这个过程将导致水下滑翔机自身重力的改变，即水下滑翔机姿态变化的驱动力产生源于电池包移动和回排油动作引起的自身的重力和重心的改变。

针对上述分析，本文将海燕-Ⅱ水下滑翔机载体质量分为3个部分：调整水下滑翔机姿态的内置电池包及其附属可移动质量块(以下简称“可移动电池包质量块”)的质量mp、水下滑翔机的静态质量ms和可变质量mb。然后建立图2所示的体坐标系e0e1e2e3和惯性坐标系E0ijk。质量块沿着e1方向的移动可改变水下滑翔机重心在垂直纵剖面的位置，进而改变自身的俯仰角来改变水下滑翔机在不同深度下的运动性能。通过改变可变质量块的质量mb1和mb2的大小来实现水下滑翔机的上浮和下潜运动。图2中，G表示为水下滑翔机的重力，B为浮力，FL为机翼在水动力下产生的升力，v为水下滑翔机的速度，FD为沿水下滑翔机速度反方向的阻力，θ为俯仰角，α为攻角，σ为滑翔角。

图2 海燕-Ⅱ水下滑翔机体坐标系与惯性坐标系Fig.2 Petrel-Ⅱ gliders inertial frame and body frame

当水下滑翔机设计完成后，壳体和内部固定设备的质量、配平质量块的质量以及前后导流罩不跟随回排油动作变化的海水质量为静态质量，各质量关系如下：

ms=mh+mw+mz

(1)

m=ms+mp+mb1+mb2

(2)

其中，m为水下滑翔机总质量；mh为不变质量，包含自身壳体质量和内部固定设备的质量；mw为前后导流罩及其他不跟随回排油动作变化的海水质量；mz为配平质量块的总质量。可变质量mb可分为两部分，mb1为内油箱可变油液质量，mb2为外油囊油液质量及前导流罩内可变海水质量的总和。由此可知，mb1与mb2是关联的，泵机每向外泵出体积Vb的油液，内油箱质量会减小ρoilVb，与此同时，外油囊会增加相同质量的油液，但是该部分油液会将前导流罩内的海水通过排水孔挤压出去，这部分海水质量为ρVb。因此，水下滑翔机外油囊处的质量变化为(ρVb-ρoilVb)，即当水下滑翔机处于排回油的变质量过程时，内油箱与外油囊质量都会变化，整体质量大小与质心位置也都会变化。按照上述理论，将水下滑翔机浸水舱内充满的海水作为水下滑翔机本身的一部分，可以认为水下滑翔机在排回油过程中的表征浮力(该浮力由表征体积计算得到)与浮心位置不发生变化，这有助于将水下滑翔机浮心作为原点进行动力学建模。

各个质量点在体坐标系中的位置分别为矢量rs、rp、rb1和rb2，可求得重心的位置矢量：

(3)

1.2 水下滑翔机纵垂面动力学模型

本文主要研究海燕-Ⅱ水下滑翔机垂直面内的运动，需要求得其纵垂面动力学模型，即将三维的动力学模型局限到惯性系的E0ik平面和体坐标系的e0e1e3平面。将水下滑翔机电池包的移动视为缓慢的过程，忽略动质量块与壳体质量块间的相互作用力，仅考虑动质量块位置、净浮力和水下滑翔机运动状态之间的关系，给出如下动力学模型：

(4)

(5)

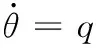
(6)

(7)

(8)

(9)

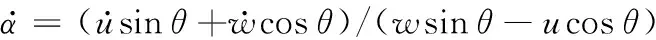
(10)

1.3 海水密度变化和壳体变形下的水下滑翔机纵垂面运动

海洋深度对海水压力、温度、盐度等物理性质有显著影响，海水密度与压力、温度以及盐度直接相关。随着水下滑翔机下潜深度增加，其外部壳体会随海水压强的增大产生压缩变形，同时海水密度也会发生变化，这会显著影响水下滑翔机的浮力大小。YANG等[12]利用多项式拟合出了海水密度随深度变化的关系，同时引入了该型号水下滑翔机壳体的压缩性因子Kvh，该压缩性因子表示水下滑翔机壳体体积变化与深度的关系。李昊璋[13]根据日本海洋数据中心(JODC)1992年12月在经纬度为142°34.95′E、11°22.78′N海域的温盐深数据进行分析，获得了深渊海水温度与深度、海水密度与深度的拟合关系式；之后根据深渊水下滑翔机同时包含有圆柱形、球形耐压舱以及含补偿液浸水舱的特点，计算了整个水下滑翔机的压缩性因子。本文研究的海燕-Ⅱ水下滑翔机仅涉及圆柱形耐压舱，其压缩性因子可通过实验测量直接得到。

将本文海上试验海域的密度-深度曲线采用相同方法拟合，如图3所示。

图3 试验海域海水密度与深度变化曲线Fig.3 Variation curve of seawater density and depth in the experimental sea area

海水在水面的密度最小值为1022.4 kg/m3，1000 m深度处的密度最大值为1031.5 kg/m3。拟合多项式如下：

ρ=p1H4+p2H3+p3H2+p4H+p5

(11)

其中，H为海水深度。拟合曲线参数p1=-2.879×10-11，p2=7.132×10-8，p3=-6.45×10-5，p4=0.03123，p5=1022.4。

海燕-Ⅱ主体壳体是一个密封的罐体结构，具有圆柱形中部和半球形端部特征，其壳体在空气中标准大气压下的体积为

Vs=(4R+3Lb)πR2/3

(12)

其中，R和Lb分别为船体圆柱部分的半径和长度，数值分别为0.11 m和1.45 m。在给定深度下壳体的体积可以表示为

Vh=Vs-KvhH

(13)

其中，Kvh=0.271 72。

综上所述，可求得给定深度下水下滑翔机的浮力变化量ΔB和浮力B分别为

ΔB=ρVh-ρ0Vs

(14)

B=ρ0V0+ΔB

(15)

其中，水面密度ρ0=p5；V0为标准大气压下水下滑翔机的表征体积。

分析水下滑翔机不同深度重力与浮力变化可以知道，水下滑翔机在深度变化的滑翔过程中，重力不改变但是表征浮力随环境因素逐渐变化，综合分析密度和压强对水下滑翔机壳体压缩的影响可知，海燕-Ⅱ水下滑翔机浮力大小会随着深度的增加逐渐变大。由于水下滑翔机在上浮和下潜过程中净浮力的方向是不同的，下潜过程向下，上浮过程向上，这将导致下潜过程随着浮力的增加净浮力会减小，上浮过程随着深度的减小和浮力的减小净浮力也会减小，进而导致水下滑翔机运动状态的变化。

由此可知，水下滑翔机在滑翔过程中需要根据温度和盐度参数来调整俯仰舵量与深度的关系。海水密度可由水下滑翔机搭载的温盐深仪测量的参数推导得出。一般情况下，同海域的海水密度变化较为稳定，根据前剖面的海水深度-密度曲线可近实时计算出该水域的深度-密度曲线参数，进而可以更加精确地得出水下滑翔机俯仰舵量随深度变化的关系曲线。

2 水下滑翔机纵垂面控制策略分析

2.1 水下滑翔机纵垂面控制方法分析

水下滑翔机的升阻比直接决定单个相同深度剖面的滑翔距离，是评价水下滑翔机性能的重要指标之一[14]。为了尽可能达到最大的升阻比，需要调节水下滑翔机俯仰舵量使其在任意深度条件下都能达到最优的滑翔角。目前已有控制方法是通过PD跟踪控制俯仰角的数值来控制水下滑翔机的运动状态，这仅适用于假定的理想滑翔过程，实际水下滑翔机的纵垂面滑翔运动是一种浮力随着深度变化的非定常运动，各时刻运动状态会一定程度上影响水下滑翔机的攻角大小，进而影响对水下滑翔机滑翔角的控制，这样仅通过俯仰角来跟踪最优滑翔角远不如直接跟踪滑翔角的控制有效。文献[15]将水下滑翔机的运动过程视为速度恒定的定常滑翔运动，其俯仰角、攻角和滑翔角都不发生变化，这样处理能极大简化计算过程，但是实际情况下，水下滑翔机深度变化和整体速度的减小会导致攻角变化，这种变化使水下滑翔机的滑翔角计算误差变大，不利于对水下滑翔机的控制，因此，需要建立更加准确的动力学模型来计算不同深度下达到最优滑翔角的俯仰舵量。

为了在水下滑翔机攻角变化时充分控制水下滑翔运动，考虑添加PID控制器跟踪控制水下滑翔机的滑翔角，使水下滑翔机在任意深度都能处于最优滑翔角的运动状态，以实现最大的升阻比，控制流程如图4所示。

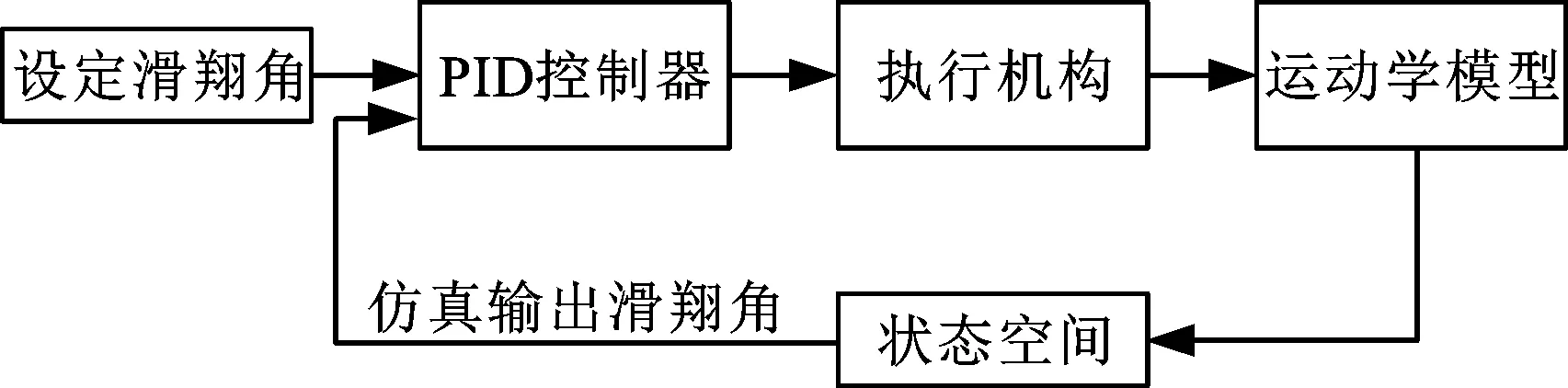
图4 PID控制器跟踪控制滑翔角Fig.4 Control flow of gliding angle tracking with PID controller

通过该优化方法可直接得到水下滑翔机各个深度下达到最优滑翔角的俯仰舵量值。俯仰舵量数值曲线相对比较固定，变化仅仅受到不同区域海水密度-深度曲线和水下滑翔机本身壳体压缩率的影响，所以，得到该曲线后可以将水下滑翔机深度作为水下滑翔机的直接控制输入量。这种控制策略相较于通过俯仰角调节水下滑翔机状态的策略将更加有效和可靠。

2.2 水下滑翔机纵垂面稳态分析

在攻角存在的条件下，可以得到滑翔角的范围为[16]

其中，KD0、KD、KL0、KL分别为零攻角总阻力系数、总阻力系数、零攻角总阻力系数、总升力系数。

由上述分析可知，任意类型的水下滑翔机均可根据水动力参数计算临界滑翔角，但水下滑翔机的滑翔角越接近于临界角度其自身稳定性越低，反映到仿真模型上则运动曲线快速失真，无法通过数值求解得到临界滑翔角下的其他运动变量。实际中水下滑翔机为了保持抗干扰能力，需要尽可能保证一定的速度，因此，不能为了追求最大的升阻比而选择最小的滑翔角。为了保证水下滑翔机能较长时间持续稳定运行，本文将滑翔角设定为∓21°，通过多次仿真测试证明该滑翔角是保证海燕-Ⅱ水下滑翔机稳定滑翔的最优值。

3 实验数据与仿真结果分析

3.1 水下滑翔机动力学数值仿真

本文使用MATLAB仿真平台，仿真对象为海燕-Ⅱ水下滑翔机模型，通过CFD软件FLUENT计算了攻角变化过程中水下滑翔机受到的水动力和力矩，并通过最小二乘法拟合得到水动力系数如表1所示。

表1 海燕-Ⅱ总体水动力参数[17]

本模型将水下滑翔机的中性状态作为仿真初始状态，此时水下滑翔机内油箱油量(即油箱内存有的油液体积占总油箱体积的百分比)为40%，下文用Z表示，俯仰舵量为0。相关参数如表2和表3所示。

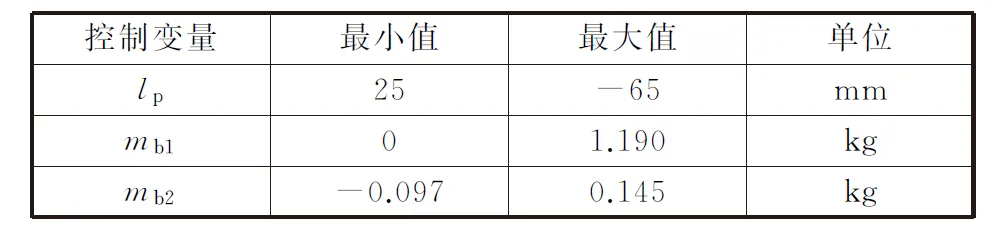
表2 水下滑翔机的控制变量

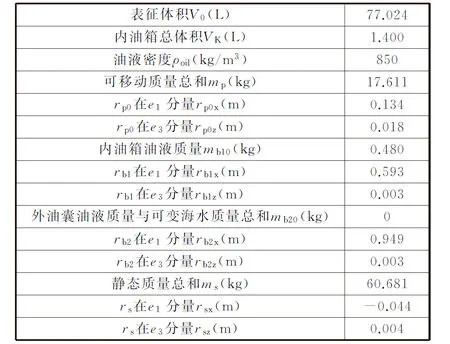
表3 中性状态下的几何与物理参数

3.2 仿真试验结果与分析

设置水下滑翔机下潜过程中内油箱油量为80%，俯仰角为-20°；上浮过程中内油箱油量为20%，俯仰角为20°。通过采用与实际水下滑翔机相同的PD跟踪控制俯仰角，并设置与目标值相差5°时开启调控，MATLAB仿真结果如图5～图9所示。

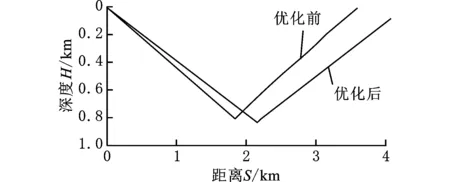
图5 优化前后水下滑翔机纵垂面运动轨迹Fig.5 Vertical trajectory of underwater glider beforeand after optimization

图6 优化前后水下滑翔机工作深度与时间关系Fig.6 Relationship between working depth and time ofunderwater glider before and after optimization

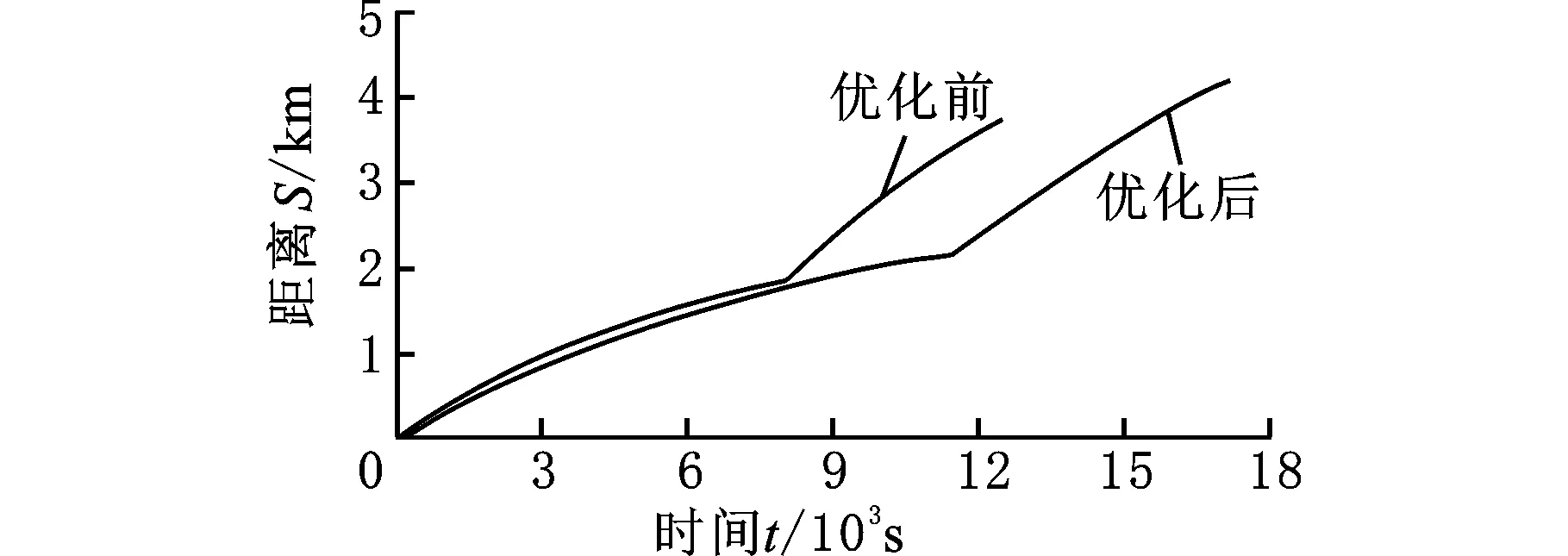
图7 优化前后水下滑翔机滑翔距离与时间关系Fig.7 Relationship between glide distance and time ofunderwater glider before and after optimization

图8 水下滑翔机各角度与时间关系Fig.8 Relationship between angle and time of underwater glider

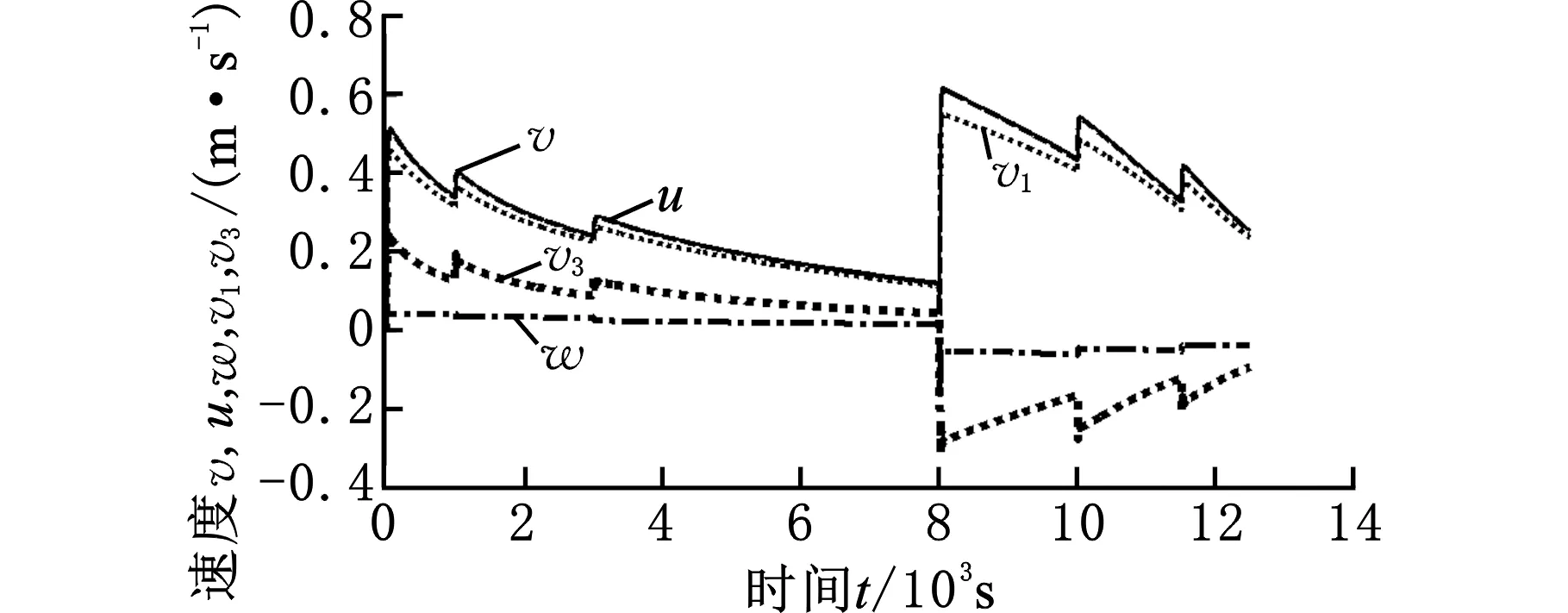
图9 水下滑翔机各速度与时间关系Fig.9 Relationship between speed and time of underwater glider

由图5中优化前水下滑翔机的轨迹可以看出水下滑翔机做V字形运动。

由图6可知，下潜时间约是上浮时间的两倍，两者深度变化相同，说明上浮过程垂直方向的平均速度高于下潜过程垂直方向的平均速度。

由图7可知，下潜和上浮过程两者的水平距离基本相同，0.8 km深度剖面水平滑翔距离约为相同的1.8 km。同时，通过分析斜率也可以印证上浮过程的速度大于下潜过程的速度。另外，观察到两个过程的曲线都是凸的，说明无论是上浮还是下潜过程的水平速度都在逐渐减小，这与水下滑翔机净浮力变化趋势相同。

图8为水下滑翔机俯仰角θ、滑翔角a和攻角σ随时间的变化曲线。滑翔角和俯仰角的变化趋势相同，都是逐渐向0°偏移，滑翔角σ调整幅度比俯仰角和攻角小，下潜过程滑翔角的最大值为-22°，上浮过程最小值为21°，与2.2节海燕-Ⅱ水下滑翔机的最优滑翔角∓21°相符。此外，俯仰角在超出其临界俯仰角度∓15°时会通过调节俯仰舵量将俯仰角调整至∓20°附近，因此，水下滑翔机的俯仰角θ会在-20°～-15°或15°～20°范围内调整。攻角α的变化趋势是逐渐向远离0°偏移，偏移绝对值在5°～8°范围内。可以发现，水下滑翔机以俯仰角作为控制参考量、俯仰舵量作为控制量时的调整过程对俯仰角、滑翔角和攻角随深度的变化有抑制作用。

图9表示水下滑翔机速度与时间的关系，包括体坐标系下和惯性坐标系下的速度，两者数值满足式(4)和式(5)的转换关系。由图可知，无论水下滑翔机处于下潜或上浮阶段，速度均逐渐减小，体坐标系下最大速度为下潜转上浮的初期阶段，大小为0.55 m/s；最小速度为排油前时刻，大小为0.18 m/s。图中水下滑翔机的水平速度和垂直速度也逐渐减小，速度变化与图6和图7结果相符。

水下滑翔机净浮力会显著影响运动状态，但是过大的净浮力并不会有效增强水下滑翔机的运动性能，相反可能会造成水下滑翔机不必要的能量损失。例如，排油下潜转上浮时的净浮力相对于下潜过程偏大，但滑翔距离的增加不明显。另外，泵机的功率受外界环境影响，外界压力越大泵机的功率也需要相应增大，这会产生大量的能量浪费，但在深度较浅的海域排油时，排油抵抗的海水压力较小，能一定程度降低功耗，因此，在排油下潜转上浮切换的过程中可以采用分段排油的控制方法，先让泵机向外排出一部分油液使水下滑翔机的净浮力方向改变，直到水下滑翔机上浮滑翔到较浅的深度再将剩余的油液泵出，以达到降低功耗增加续航的目的。

3.3 海上试验数据验证

2019年5月12日—6月1日，项目组在南海北部海域进行了海上试验，试验区域及水下滑翔机(HY08)航行轨迹如图10所示。

图10 HY08水下滑翔机海上试验航行轨迹Fig.10 Sea trial trajectory of HY08 underwater glider

HY08水下滑翔机总计运行85个剖面，平均深度930 m，随机选取水下滑翔机稳定航行数据中第39剖面的实际运行数据与仿真进行对比，结果见图11～图14。

图11 水下滑翔机内油箱油量与时间的关系Fig.11 Relationship between fuel volume and time inunderwater glider

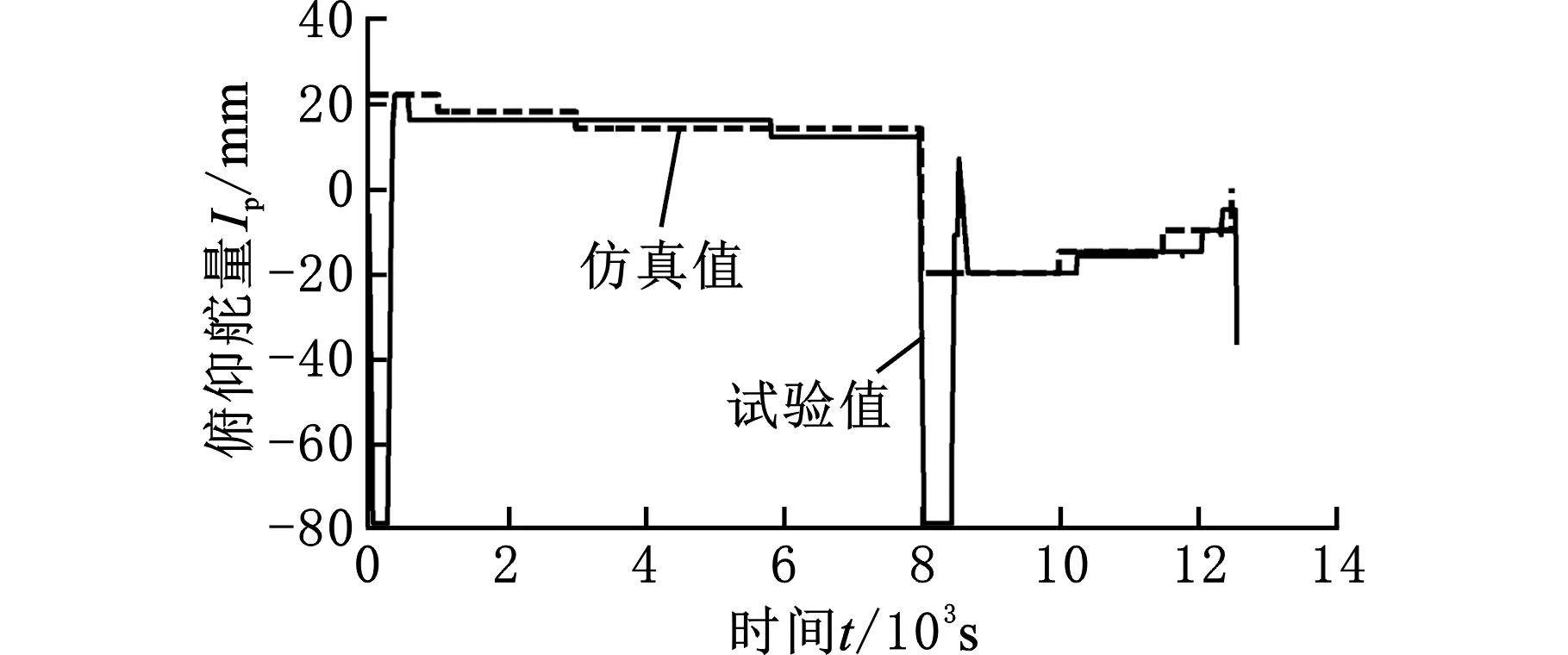
图12 水下滑翔机俯仰舵量与时间的关系Fig.12 Relationship between pitching rudder and timeof underwater glider

图13 水下滑翔机工作深度与滑翔时间的关系Fig.13 Relationship between working depth andgliding time of underwater glider

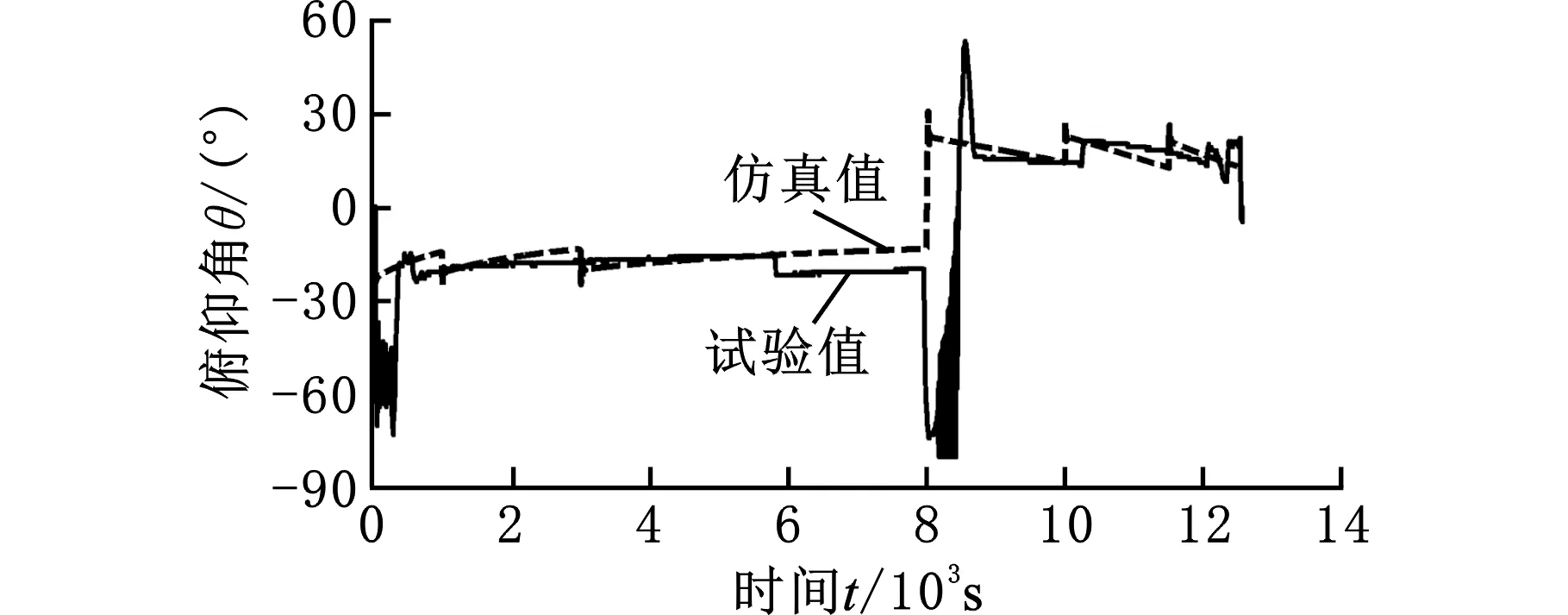
图14 水下滑翔机俯仰角度与时间的关系Fig.14 Relationship between pitch angle and time ofunderwater glider

图11所示为水下滑翔机海上试验时内油箱油量与仿真油量对比。试验油量与仿真油量有5%的偏差，原因是该试验样机实际配平油量与设计配平油量之间有差异，这种差异受不同海域海水密度影响(水下滑翔机的配平过程基于某一海域水面的海水密度计算)，因此，该误差属于正常的实验误差，之后在多次采集该试验区域的温盐深数据后可以修正该误差。

图12所示为水下滑翔机俯仰舵量海上试验数据与仿真数据对比。两者相近，变化趋势也相同，下潜和上浮过程都是随着水下滑翔机深度的变化对俯仰舵量的控制逐渐向0舵量值靠近。

图13所示为水下滑翔机工作深度海上试验数据与仿真数据对比。对比可知，两者下潜时间均为8×103s，上浮时间均约为4×103s，两者曲线变化相近。

图14所示为水下滑翔机俯仰角度海上试验数据与仿真数据对比。两者数值接近且变化趋势相同，当俯仰角度超过水下滑翔机设定的俯仰角度阈值时，俯仰舵量的调控会显著改变整个水下滑翔机的姿态。对比下潜和上浮过程中的俯仰角度变化可知，上浮过程俯仰角度的变化更加剧烈。同时，为了保证俯仰角度在设定的范围内，对俯仰舵量的调控需更加频繁，这是由于下潜过程与上浮过程中的净浮力大小有差异，该差异是为了保证水下滑翔机有足够动力上浮并能以一定姿态漂浮在海面上，特别是在水下滑翔机处于漏水或者紧急情况净浮力不足时仍然可保证水下滑翔机正常上浮。

一般地，在实际海上试验过程中水下滑翔机做三维运动，由于海流等环境不确定性，海上试验数据与仿真结果不可避免地有一定差异。对比分析图13和图14可知，考虑海水密度与壳体变形的因素，仿真数据的变化趋势与试验数据基本相同，其中最明显的特征是水下滑翔机下潜过程的深度变化曲线是凹的，上浮过程是凸的，且俯仰角度变化趋势完全相同，即随着俯仰舵量的改变，俯仰角度的变化相同，表明本文建立的仿真模型是准确和可靠的。

由图9可以看出，在油量不变的条件下，水下滑翔机速度变化十分明显，这与我们一般认为的定常滑翔运动不符。由此可以推断，即使在滑翔过程中水下滑翔机外部油囊的体积不发生变化，其本身浮力的变化也会影响运动状态，通过俯仰角作为参考量的控制策略在整个水下滑翔机的运动过程中的控制能力会减弱，水下滑翔机的控制方法还有待改进。

3.4 控制策略优化仿真

由于将水下滑翔机俯仰角作为控制参考量的控制能力不足，本文直接将滑翔角作为控制参考量对水下滑翔机进行控制，过程如图4所示，采用PID控制器跟踪控制滑翔角，设定水下滑翔机下潜过程中内油箱油量为80%、滑翔角为-21°，上浮过程中内油箱油量为20%、滑翔角为21°，得到的仿真结果如图5～图7和图15～图17所示。

图15 优化后水下滑翔机各角度与时间的关系Fig.15 Relationship between glide angle and time after optimization

图16 优化后惯性坐标系下水下滑翔机速度与时间的关系Fig.16 Relationship between velocity and time of underwater glider after optimization

图17 优化后水下滑翔机俯仰舵量与时间的关系Fig.17 Relationship between pitch rudder and time ofunderwater glider after optimization

综合分析图6和图7可知，直接将最优滑翔角作为控制参考量，单个0.8 km深度剖面的航行时间优化后比优化前增加约80 min，滑翔的水平距离优化后比优化前增加约530 m，增长率为14.1%。

图15表示水下滑翔机在PID控制器下跟踪滑翔角为∓21°时，各角度随时间变化的仿真结果。结果表明，该PID控制器能有效地将运动模型的滑翔角维持在∓21°附近。在这个过程中，水下滑翔机的俯仰角和攻角数值都会变化，但是均满足图2所示的|σ|=|α|+|θ|。

图16所示为优化后水下滑翔机各速度与时间的关系，包括体坐标系下和惯性坐标系下的速度，数值满足式(4)、式(5)的转换关系。观察可知，水下滑翔机总体速度的变化和优化前相同，下潜和上浮过程速度逐渐减小，添加了PID控制器后速度变化更加平稳，没有产生大幅度改变俯仰角带来的速度波动。

图17所示为优化后水下滑翔机的俯仰舵量数据与试验数据对比，发现两者在上浮或下潜的过程中，俯仰舵量数值变化趋势相同，都是向0舵量缓慢间歇性偏移。

综合分析，优化后考虑到攻角变化并直接通过最优滑翔角作为控制参考量的控制策略能有效提高同深度剖面的航行距离。此外，可以通过对比图13和图17得到下潜或上浮过程不同深度最优滑翔角对应的俯仰舵量，可以将该参数作为试验水下滑翔机控制的直接参数。进一步分析图17可知，在该优化控制策略下，水下滑翔机下潜或上浮的过程中俯仰电机的运动为间歇性单向运动，其中下潜过程俯仰舵量由23.5 mm逐渐变为15.5 mm，上浮过程俯仰舵量由-19 mm逐渐变为-12 mm。同时，试验俯仰舵量在下潜过程由22 mm逐渐变为12 mm，上浮过程由-20 mm逐渐变为-5 mm。从做功的角度对比优化后的数据与依靠PD控制俯仰角调节水下滑翔机运动状态的试验数据，两种策略所消耗的能量差别不大，因此，可以得出依靠水下滑翔机的动力学模型跟踪最优滑翔角的控制策略是有效的。

4 结论

本文详细分析了水下滑翔机以重心位置改变导致姿态变化的运动行为，讨论了在正常滑翔运动过程中水下滑翔机的浮力随海水密度与压强增大而逐渐增大，从而导致净浮力减小的运动过程。在此基础上建立了水下滑翔机纵垂面变浮力过程的动力学改进模型，该模型能正确反映水下滑翔机在任意深度的运动状态。对最优滑翔角的跟踪控制可以有效增强水下滑翔机在单剖面的运动距离，并且不会产生额外能量消耗。该控制策略不仅适用于水下滑翔机，且可拓展应用到一般的水下航行器。

由于洋流的速度在不同区域或不同深度均有不同，在洋流影响下，水下滑翔机最优滑翔角会发生相应变化。此外，任意时刻水下滑翔机的最优滑翔角与水下滑翔机的水平速度相关，不同深度下水下滑翔机的水平速度与当前深度下的迎流速度是计算水下滑翔机在该状态下最优滑翔角的关键参数。未来工作会将观测海域的流场作为干扰项，在三维空间内进行模型的完善，建立更准确的动力学模型。