机器学习方法拟合宏观经济变量优于传统统计方法吗——基于经济政策不确定指数的拟合

袁 靖 刘 响 董雅菁 马 腾

（山东工商学院 统计学院，山东 烟台 264005）

一、引言及文献综述

经济政策是为实现既定的宏观经济目标、增进社会福利而制定的解决经济问题的指导原则和措施。受经济政策自身特征和国内外环境因素的影响，经济政策往往具有不同程度的不确定性，即未来与经济相关的政策变动中包含的各类无法预知的成分。近年来，突发事件凸显不确定冲击是影响宏观经济运行的主要冲击，尤其经济政策不确定是引起宏观经济波动的原因，并且对经济变量总体上表现为负面效应（Bloom，2009；Caggiano等，2014；Jurado等 2015；Arouri等，2016；Dinb 等，2018；Dayorg zhang 等，2019；Tao Li等，2019；Shen Huayu 等，2021；FengHe等，2020；Dhole等，2021；Altig等，2020）。2020年全球爆发了新冠肺炎疫情，疫情凸显不确定性对经济造成巨大冲击，随着经济环境不确定性增强，经济政策不确定指数的波动也呈现长期加强趋势。

对经济政策不确定指数（EPU）的构建，最具代表性的是Baker等（2016）利用媒体文本，分析构造的经济政策不确定性指数，研究者选取各个国家主流报纸构建相关词库，通过词频统计构建经济政策不确定性指数（EPU指数），该指数被广泛使用。我们可以从网站http：//www.policyuncertainty.com下载26个国家的EPU数据。已有文献对EPU的分析均为EPU对经济波动的影响效应分析，对EPU波动拟合的文献仅有一篇，文章采用高维VAR模型，基于18个发达国家的EPU，对巴西、中国、印度、俄罗斯（金砖四国）的EPU进行了拟合。

近年来，宏观经济预测领域应用ML方法的研究日益增多（Ahmed 等，2010；Stock 和 Watson，2012；Li和Chen，2014；Kim 和 Swanson，2018；Smeekes 和 Wijler，2018；Chen 等，2019；Milunovich，2020；Coulombe 等，2020），采用计量经济模型AR和随机森林、神经网络以及增强树三种机器学习方法重点预测了美国经济的五个代表性宏观经济指标：工业生产、失业率、消费者物价指数、10年期国债固定到期利率与联邦基金利率之差和住房开工率。结论认为，机器学习非参数非线性是最显著的特征，因此大大提高了所有宏观经济变量的预测精度，特别是在大数据背景下做长期预测时效果更为显著。

本文采用ARIMA模型、BP神经网络、长短期记忆神经网络LSTM以及将统计方法与机器学习融合在一起的随机森林分位数回归方法，对美国、英国的经济政策不确定指数进行拟合对比，拟合效果显示，长短期记忆神经网络LSTM预测效果最优，ARIMA模型拟合效果最差，相同样本期内ARIMA模型拟合均方根误差几乎达到LSTM方法预测均方根误差的3倍，随机森林分位数回归及BP神经网络拟合效果居中。这为今后采用机器学习方法对宏观经济变量进行拟合及预测提供了新思路。

二、机器学习方法及ARIMA模型

（一）BP神经网络

BP神经网络是一种多层前向神经网络，由于在网络的训练中，调整权阈值的训练算法遵循了误差反向传播方式，所以它是神经网络中比较成熟和完美的一部分。通常BP神经网络是一种具有3层或者3层以上神经元的神经网络，包括输入层、隐含层和输出层，上下层之间实现全连接，但同一层神经元之间无连接。

（二）长短期记忆神经网络 STM

LSTM模块由多个同构单元格构成，单元格常被称作节点。每个节点内部包括遗忘门、输入门、输出门以及由它们控制的输入到输出的各种连接。三个门是LSTM的核心，可以看作是在LSTM内部流动时的调节者。具体功用如下：遗忘门负责对此前状态空间中的信息进行过滤调节；输入门调节各节点输入信息进入状态空间的比例；输出门对当前节点下状态空间所保存的信息流入隐层的过程进行调控。

（三）随机森林分位数回归

随机森林是通过集成学习的思想将多棵树集成的一种算法，它的基本单元是决策树，而它的本质属于机器学习的一大分支——集成学习方法。随机森林算法是一种非线性模型，即将多个决策树集成为森林的一种模型。分位数随机森林（QRF）由分位数回归和随机森林发展得到，但保留了两种算法的优点，其输出值为不同分位点的回归预测结果。QRF运算速度快，模型性能受参数影响小，且具有较强容噪性。

分位数回归森林可以被看作是一个适应性近邻分类和回归过程。对每一个X=x，都可以得到原始n个观察值权重集合 wi（x），i=1，2，...，n。记 θ为随机参数向量，决定决策树的生长（比如每个结点对哪些变量分割），对应的决策树记为T（θ），记B为X的域。

具体说，设训练样本为（Xi，Yi），i=1，...，n，其中特征向量X为P维，即X∈Rp。决策树是一种树形结构，其中每个内部节点基于一个属性进行测试，根据测试结果的不同继续分配到不同的分支，每个叶节点代表最终输出的类别，设θ为单颗决策树的参数，决定每个节点的分裂变量和树的深度等条件，决策树的叶子节点记为l，l=1，...，L。每个样本的特征向量x都属于叶子中的一个区域，记为X∈Rl，同时将这个节点记为l（x，θ）。对训练样本Xi，考虑其对应叶子节点上的权重向量wi（x，θ）为：

式中，（I·）为示性函数，显然上式的权重和为1。

对随机森林算法来说，新观测值条件均值的估计E（Y|X=x）即为k棵决策树的平均。设每棵决策树的参数 θt为独立同分布，t=1，...，k，则权重向量w（ix）为各个决策树平均：

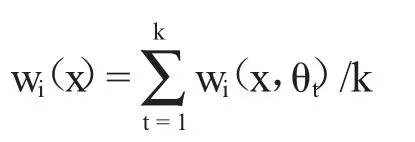
则随机森林最终的预测为对因变量的加权平均：

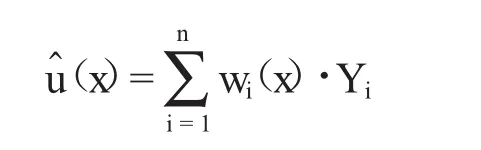
分位数回归森林建立在随机森林的基础上，对因变量全部的条件分布进行估计，设给定条件X=x时因变量Y的条件分布为：

利用随机森林估计的权重wi（x），条件分布的估计可以看成对示性函数I（Yi≤y）的加权平均，因而给出对条件分布的估计为：

进一步可得到利用样本数据估计的Y的条件分位点Qτ（Y）

分位数回归森林中，模型的参数主要有两个，分别为树的数量和每个节点参与分裂变量的个数。这里：对最优参数的选取方法为：在样本内数据集上进行训练，使该参数建立的模型在样本内失败个数N更接近于理论失败个数。

（四）ARIMA 模型

具有如下结构的模型称为求和自回归移动平均模型，简单记为 ARIMA（p，d，q）模型：

式中，Δd=（1-B）d；Φ（B）=1-φ1B-L-φpBp，为平稳可逆ARMA（p，q）模型的自回归系数多项式；Θ（B）=1-θ1B-L-θqBq，为平稳可逆 ARMA（p，q）模型的移动平滑系数多项式。ARIMA模型的建立和预测方法已经成熟，因此，利用合理阶数的差分运算来平稳化，就能满足对非平稳系统输出简便有效的建模。

三、基于机器学习方法及ARIMA模型对经济政策不确定指数拟合

（一）数据

本文选取美国经济政策不确定指数、英国经济政策不确定指数历史数据（美国数据从1985年1月1日至2021年3月19日，英国数据从2001年1月1日至2021年3月19日），数据来源为http：//www.polic yuncertainty.com/index.html。

（二）拟合评价指标

确定性点拟合误差评价指标采用平均相对误差（Mean Percentage Error）和均方根误差（Root Mean Square Error）统计，分别按以下方法计算：

1.平均相对误差δ

2.均方跟误差（RMSE）

（三）美国、英国经济政策不确定指数拟合效果对比分析

1.BP神经网络构建、参数调优及拟合结果

BP神经网络以EPU滞后数据为特征向量从输入层输入，因此采用滑动窗口法得到输入矩阵，具体方法为：依次将美国、英国EPU数据的n个滞后值作为特征向量输入，当前EPU数据作为输出，构建前n个EPU数据和之后1个EPU数据的非线性映射，最终m个EPU样本观测值滑动生成m-n个训练集样本，即（m-n）×n输入矩阵。本文输入层的节点数目为8，输出层的节点数目为1，根据美国1985—2021年EPU数据，滑动生成10575个训练集样本，根据英国2000—2021年EPU数据，滑动生成7375个训练集样本，绘制BP神经网络模型的拟合曲线，并用虚线表示测试集真实的EPU数据，实线为BP神经网络拟合EPU指数，图1为美国、英国经济政策不确定指数BP神经网络全样本拟合图，美国EPU拟合均方根误差为63.87，英国EPU拟合均方根误差为140.14。

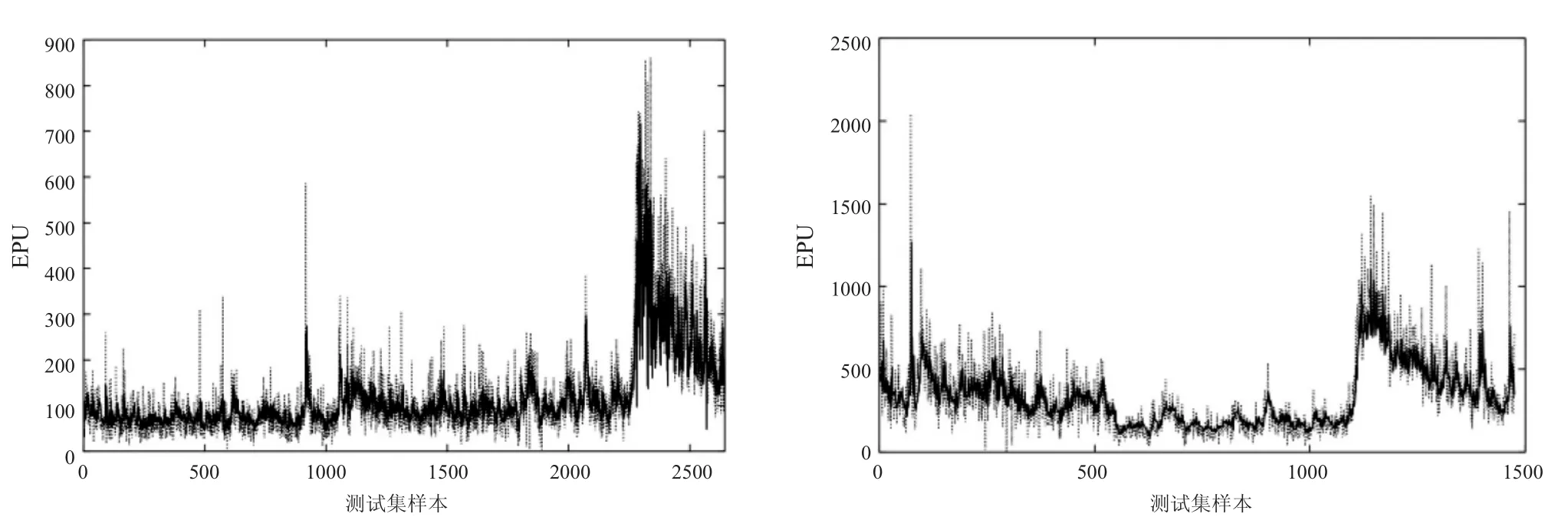
图1 美国、英国EPU的BP神经网络全样本拟合图

2.长短期记忆神经网络LSTM构建、参数调优及拟合结果

在单步EPU指数多维数据自回归模型中，采用每步长都即时更新的真实历史数据进行序列自回归，即时间滑动窗口每向下移动一步时更新真实历史数据，输入的数据维度为[1，7]，记录预测值，绘制随每次迭代的损失函数变化图像。为防止拟合LSTM层的神经元个数过多，模型总计四层，经调整后模型具体参数如下：

第一层：LSTM层，神经元个数为4个，输入步长为8，单步多维序列自回归数据输入维度为7。

第二层：隐藏层，神经元个数为4个。

第三层：全连接层，输出神经元个数为1，激活函数为linear线性激活。

图2为美国、英国经济政策不确定指数LSTM全样本测试集的拟合图，虚线为EPU真实值，实线为EPU拟合值，美国EPU拟合均方根误差为60.12，英国EPU拟合均方根误差为128.31。

图2 美国、英国EPU的长短期记忆神经网络LSTM全样本拟合图

3.随机森林分位数回归参数选择及拟合结果

基于多次实验，选择树的数量为500，分裂变量为自动选取优化。图3为随机森林方法对美国、英国EPU的拟合图，虚线为真实值，实线为拟合值，美国EPU拟合均方根误差为61.19，英国EPU拟合均方根误差为138.26。

图3 美国、英国EPU的随机森林分位数回归全样本拟合图

4.ARIMA模型拟合效果

根据AIC和BIC准则，确定美国EPU数据的最优模型是 ARIMA（4，1，2），英国 EPU 数据的最优模型是 ARIMA（1，1，1），绘制 ARIMA 模型的拟合曲线如图4所示，其中虚线表示测试集真实的EPU数据，实线为ARIMA模型拟合的EPU指数，美国EPU拟合均方根误差为169.25，英国EPU拟合均方根误差为142.08。

图4 美国、英国EPU的ARIMA模型拟合图

5.总结

我们将四种方法对美国、英国EPU拟合效果总结如下：

表1 误差比较

由此可以得出结论，长短期记忆LSTM方法拟合美国EPU拟合效果最优，传统ARIMA模型拟合效果最差，其均方根误差几乎是长短期记忆LSTM方法拟合均方根误差的3倍，BP神经网络及随机森林分位数回归方法居中。长短期记忆神经网络LSTM在经济学现有文献中均用于股票收益率预测，本文将其运用于宏观经济变量EPU拟合，效果很好。对英国EPU拟合效果，四种方法拟合均方根误差差异接近，由于英国EPU数据时间维度不如美国EPU数据时间维度长，因而采用机器学习方法拟合效果虽好但不明显。

四、结论

机器学习与统计学的交叉已经成为经济学的重要研究领域。由于大数据的可用性，特别是在微观经济应用中，机器学习方法已经得到重视（Belloni，2017和Athey，2019）。

本文采用机器学习与计量经济模型相结合的方法对美国、英国历史EPU数据进行拟合，由于机器学习方法能够体现数据的非线性特征，因而拟合效果优于传统统计模型（ARIMA模型），这与Coulombe等（2020）的研究结论是一致的。数据时间维度越长，采用机器学习拟合效果越好，数据时间维度短则机器学习优越度不明显，换句话说，在大数据背景下机器学习方法的优良性能够更好地显现出来。对宏观经济核心指标进行预测一直是统计学、宏观经济学等领域的重要研究课题，近年来我国学者致力于改进预测模型，提高预测精度，随着未来经济环境的不确定性增加，非线性日益成为经济变量显著特征，在宏观经济高度不确定性、金融压力及经济衰退时期，非线性的表现尤其被放大，此时机器学习方法在预测宏观经济变量时表现出优越性，因而未来机器学习方法将更多适用于宏观经济预测。