基于区间权重组合预测方法的GDP预测实证
2022-01-24王洪霞周姣姣
王洪霞 周姣姣
(1.河南财经政法大学 统计与大数据学院,郑州 河南 450046;2.河南省教育统计数据分析与研究中心,郑州 河南 450046)
一、引言
2013年我国政府创造性地提出了宏观调控的新模式,即区间管理。区间管理要求宏观经济从点目标管理向区间目标管理转变。预测是管理之魂,区间管理首先要从区间预测开始。因此,如何对宏观经济进行区间预测值得研究。
对宏观经济进行区间预测,极具现实意义。一方面,由于不确定性因素的存在,很难得到精确的点值预测,而区间预测值相对容易获得;另一方面,对经济政策制定而言,宏观经济区间形式的预测值既能反映GDP未来的水平又能反映其波动状况,比点值预测更具参考价值。正如《新京报》2019年1月20日的报道,北京、福建和河南等5省市政府工作报告中将GDP增长目标设定为区间值,加设上下限。
为了得到区间预测值,传统方法是基于不同的计量模型,如经典的ARMA、VAR、GARCH等模型,通过点估计和模型标准偏差来构建变量的置信区间。然而,该方法过于狭隘以至于不能够实现理想的区间覆盖(Gardner,1988;Granger,1996),通过点估计的置信区间得到的未来变量波动幅度和现实中的变量变动区间具有本质上的不同(韩艾和陈曦等,2008)。
组合预测方法在GDP预测中被广泛应用。这方面的研究较多,王莎莎和陈安等(2009)基于多个时间序列模型的组合对我国GDP进行了预测;游文倩和庄科俊(2020)基于ARIMA模型和Holt-Winters无季节性模型构建了组合预测模型,对安徽省GDP进行了预测。组合预测方法于1969年由Bates和Granger首次提出,其是由若干不同的单一预测模型按照一定的加权方式集结而成的,总体预测效果显著优于单一模型的预测结果。此方法的关键在于如何确定权重系数。权重系数的好坏,直接影响到预测结果的精确度。对于点值实际值,如果权重系数为通常情形下的点值,则组合预测值也为点值;但如果权重系数为区间值,根据区间运算,组合预测值就是区间值。
为了得到GDP的预测区间,本文拟构建区间权重的组合预测模型,并进行GDP区间预测实证分析。
二、区间权重组合预测方法
为了确定区间权重系数,沈家骅和严振祥(2006)基于区间数学知识将其转化为一个线性规划的求解问题,其缺点是要事先确定预测精度,如果值设定的不合适,就会影响预测的可靠性。何其慧和黄德舜等(2011)基于一种误差指标构建了一个预测权重半径的最优化模型,其缺点在于区间权重系数是在点值权重基础上添加了一个权重半径构成,而不是直接由最优模型解出。上述两种确定区间权重系数的方法,均没有考虑时间序列数据的新旧程度对预测结果的影响。实际上,在时间序列预测中,离预测时间越近的数据对预测结果的影响越大,离预测时间越远的数据影响越小。殷春武(2011)提出可以在预测建模中对时间赋予一定的权重,并提出以作为时间权重。殷春武(2013)针对区间时间序列数据,研究了时间权重的组合预测方法。
参考多位学者的研究文献,本文给出具有时效性的区间权重系数的确定方法。


三、实证分析
选取全国1992—2020年GDP年度数据进行分析。首先,对GDP序列进行二次指数平滑,得到的预测结果见表1。

表1 二次指数平滑结果
预测序列在1—29期(样本数据范围)的取值是一步预测值(k=1),30—34期(预测值,即预测年份为2021—2025 年)是多步预测值(k=1,2,3,4,5),预测期内使用的预测公式是:

上式中,T=29(样本末期),截距和斜率见表1,预测效果见图1。

图1 全国1992—2020年GDP实际值序列和平滑值序列比较
接着,建立指数曲线趋势模型,其参数估计结果如表2所示。

表2 指数曲线参数的最小二乘估计
趋势模型为:

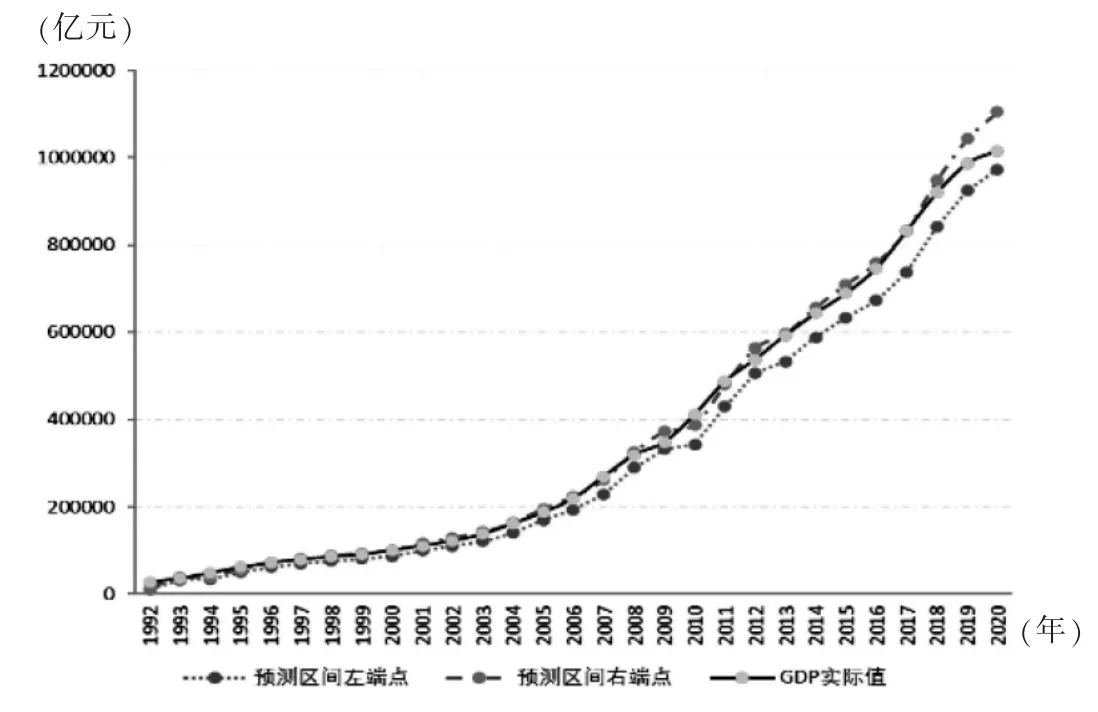
指数曲线趋势模型的预测效果见图2。

图2 全国1992—2020年GDP实际值序列和指数曲线预测值序列比较
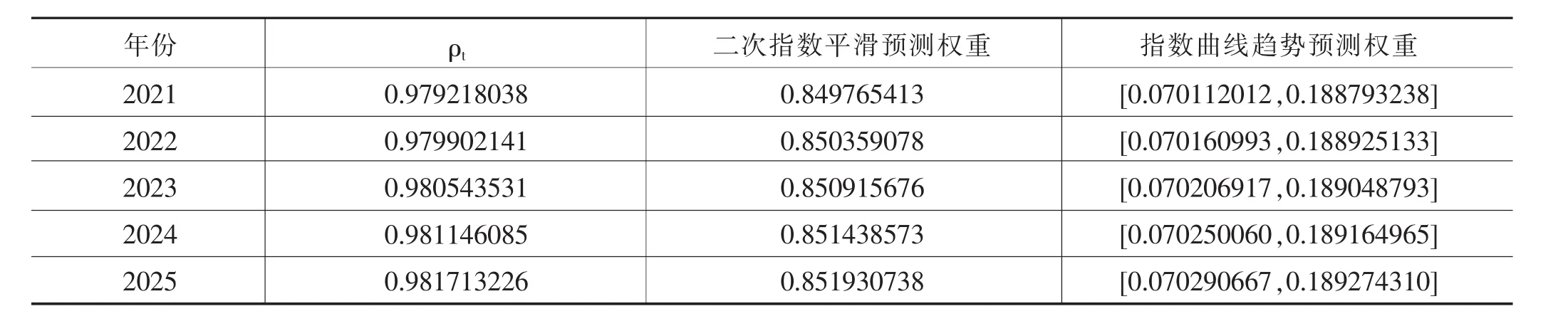
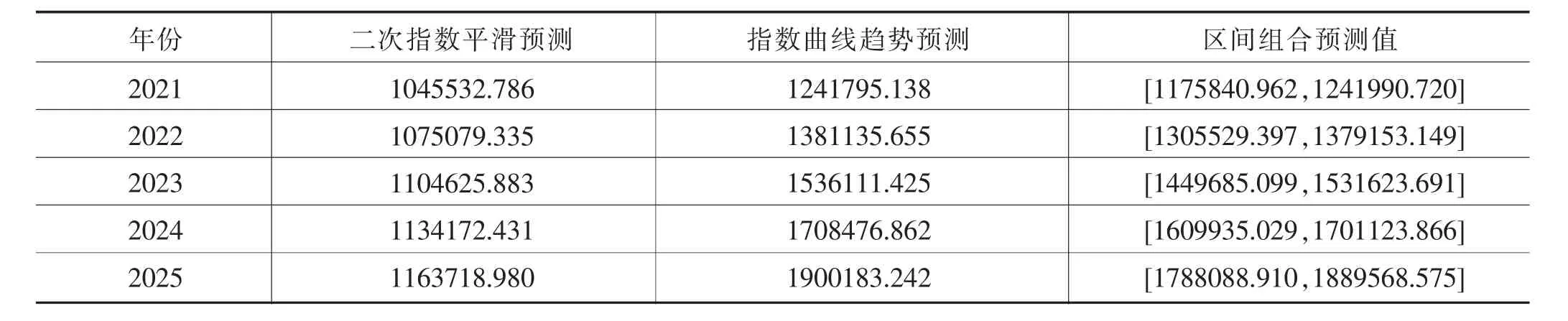
利用上述两种方法进行组合预测,假设二次指数平滑预测的权重为<ρtl1,ρtr1>,指数曲线趋势预测的权重为 <ρtl2,ρtr2>,其中为时间权重,l+l=1,120 模型(2)和模型(4)实际上是二次规划问题。将GDP实际值及预测值代入,模型(2)变形为: 利用Matlab可得l1=0.8687,l2=0.1322。 模型(4)变形可得 由图3可知,采用区间组合预测方法得到的预测区间,大多数能够包含实际值,少数的预测区间其端点值已很接近实际值。 图3 全国1992—2020年GDP实际值序列和组合预测值序列比较 以2016—2020年为例,其间GDP实际值与区间预测值的比较见表3。 表3 2016—2020年全国GDP实际值与区间预测结果单位:亿元 由表3可知,2016—2020年区间组合预测值均包含实际值,并且其半径相对于实际值的比值均小于0.1,说明区间权重组合预测方法具有一定的可行性。 组合预测中2021—2025年二次指数平滑预测的权重系数、指数曲线趋势预测的权重系数见表4。 表4 GDP组合预测中两种单项预测方法的权重 全国2021—2025年GDP预测结果见表5。 表5 全国GDP预测结果单位:亿元 组合预测方法在GDP预测中被广泛应用。为了得到GDP区间预测值,本文将传统组合预测中的权重系数替换为具有时效性的区间权重,进而拓展了组合预测方法。为了验证新方法的可行性,采用全国1992—2020年GDP年度数据展开GDP实证预测分析,研究结果表明:基于区间权重组合预测方法的区间预测值绝大多数能够包含实际值,并且其半径相对于实际值的比值均小于0.1。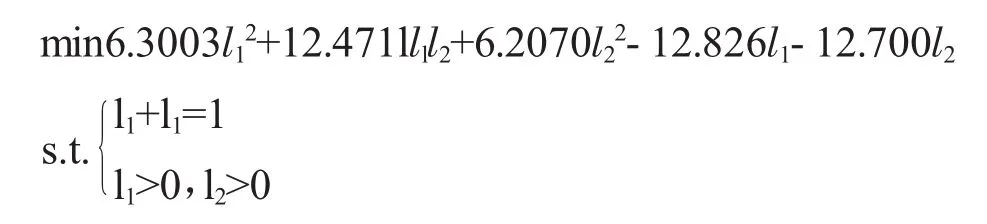


四、结论
