区域创新能力变量选择及时空协同研究

熊晓娅 杨宜平，2

（1.重庆工商大学数学与统计学院，重庆 400067；2.重庆工商大学经济社会应用统计重庆市重点实验室，重庆 400067）

一、引言

创新作为引领我国经济发展的战略性资源，深刻影响着国家前途命运，影响着人民福祉。

在全球科技创新进入空前密集活跃的时期，我国的科技创新能力还有待加强，各省（区市）之间区域创新资源集聚及创新能力的不平衡现象仍较为严重。相对于发达的东部沿海地区，西部地区创新资源投入量较少。如何更合理地投入创新资源和实现资源的最优利用，以此创造出更大的经济价值是当前社会关注的问题。

在此背景下，对我国各地区的创新资源投入以及对区域创新能力进行研究十分有必要。对于这两个问题的探索不仅有助于更为直观、科学地了解中国省域创新资源的分布与区域创新能力水平，而且可以在空间关系层面上更加明确区域创新能力的影响机制，为创新资源在全国范围内的布局、创新资源的投入提供决策依据与政策建议，具有理论和实践上的重要意义。

二、文献综述

创新作为经济增长的源泉，受到政府、企事业单位的广泛关注，区域创新能力的影响因素一直以来是学者研究的热点。周元元和冯南平（2015）选取R&D人员集聚度、R&D经费集聚度作为衡量创新要素集聚的指标，同时将政府对创新活动的资助金额作为控制变量，用专利申请量度量区域自主创新能力[1]。陈强和颜婷等（2017）将创新主体、创新网络和创新环境作为科技创新能力影响因素，认为应充分发挥高校资源对于提升科技创新能力的直接和间接作用[2]。王淑英和王洁玉等（2020）在进行创新资源指标选取时，将产业结构水平、对外开放水平和信息化水平等对区域创新绩效有一定影响的指标作为控制变量考虑其中，选取专利授权量和新产品销售收入作为创新资源集聚相关衡量指标，用R&D人员流动量和R&D资本流动量来测度创新资源流动[3]。傅雅文和顾元媛（2021）认为政府R&D补助对企业创新投入具有激励作用，且市场化程度越高、知识产权保护越强、人力资本投入越多，激励作用越强[4]。

在区域创新能力的评价方法上，吴卫红和杨婷等（2017）实证分析高校和高技术产业创新资源水平对区域创新的溢出效应，认为单一的创新资源集聚会过高或者过低地抑制经济增长[5]。张铁山和白慧林（2020）利用熵权TOPSIS法对长三角的科技创新能力进行评价，发现长三角内部科技创新发展不均衡，自主创新能力缺乏[6]。张安妮（2019）建立时空双效应空间杜宾模型（SDM模型），对创新资源集聚水平和创新能力的空间关系进行检验，得到创新资源集聚水平和创新能力具有空间依赖性，创新资源集聚水平的直接效应为正且显著等结论[7]。王淑英和王洁玉等（2020）将空间计量模型运用到创新资源研究中，分析资源流动对区域创新绩效的影响以及金融集聚在其中的调节作用，研究结果显示创新资源流动对区域创新绩效具有空间溢出效应。谢泗薪和胡伟（2021）设计经济高质量发展与科技创新两系统的评价指标体系，并测算两系统的综合指数、耦合度和协调度，在此基础上引入空间计量模型进行影响因素分析[8]。周春应（2021）运用主成分分析法测算中国30个省（区市）科技金融发展水平，构建空间计量模型研究科技金融对地区经济增长的影响，发现中国的科技金融呈现“东强西弱”态势，各地区之间存在空间正相关性[9]。

综上所述，关于创新资源对区域创新能力的研究取得了较为丰硕的成果。但对于创新指标的选取加入了许多主观因素，本文试图在现有研究的基础上，以中国31个省（区市）为研究对象，选取2011—2019年省域面板数据，使用lasso方法进行区域创新指标选择，随后讨论空间自相关（SAR）模型、空间误差（SEM）模型、空间杜宾（SDM）模型的优劣，实证分析创新资源投入对创新能力的影响机制。

三、指标选取与数据来源

（一）区域创新能力评价指标初步选取

综合诸多学者的经验，本文将创新资源归结为三大类：创新教育资源、创新财力资源和创新人力资源。

教育作为创新人才培养的基础，为区域创新能力提供了很多未知的可能，是不可忽略的因素，选取高等院校在校生数量、高等院校师生比（教师=1）、教育经费投入来衡量地区创新教育资源。

创新财力资源是一个地区对科技创新领域的资金投入量，区域创新能力的提升离不开财力的支持，一般而言，财力资源投入越多，科技创新水平往往更高，选取高技术产业产值和R&D经费内部支出来衡量地区创新财力资源。

创新人力资源是一个地区从事科技创新事业的人员，投入高技术产业和R&D从业人员，产生创新性成果，对提高区域创新能力有很大影响，选取高技术产业从业人员数量、R&D人员全时当量来衡量地区创新人力资源。

用专利申请授权数量来衡量区域创新能力水平，并使用符号y表示，具体构建指标体系见表1。

表1 区域创新能力指标体系

（二）L asso方法指标选取结果

本文选取的区域创新能力指标大多是参考已有学者的研究，但已有文献对于指标体系的选取和研究大都掺杂了较多的主观因素。因此，有必要利用统计方法对指标体系进行处理，筛选出最重要的创新能力影响因素。

首先，基于固定效应面板模型进行变量选择，模型设定如下：

其中，yit是因变量，xit是 p×q维协变量，β是（q+1）维的回归系数，αi是固定效应，εit是随机误差项，且 ε～ N（0，σ2In）。

Lasso方法在1996年由Tribshirani R提出[10]，与传统变量选择方法不同，Lasso能够同时进行变量选择和参数估计，并添加惩罚函数使得对模型影响因素较小的变量快速压缩至零，从而能够快速选择出影响因素较大的那些变量。对于式（1）的回归模型，本文用惩罚函数来估计参数β，惩罚函数的基本形式如下：

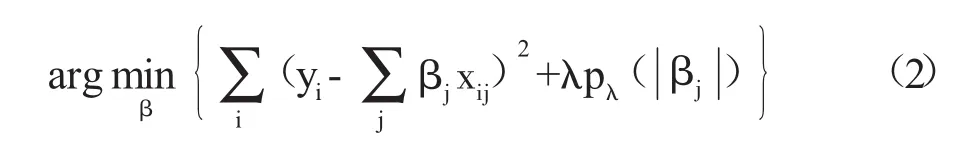
调用R软件中ncvreg、glmnet、msgps程序包，实现Lasso的变量选择，可以得到该方法具体的系数路径图和交叉验证图，如图1所示。

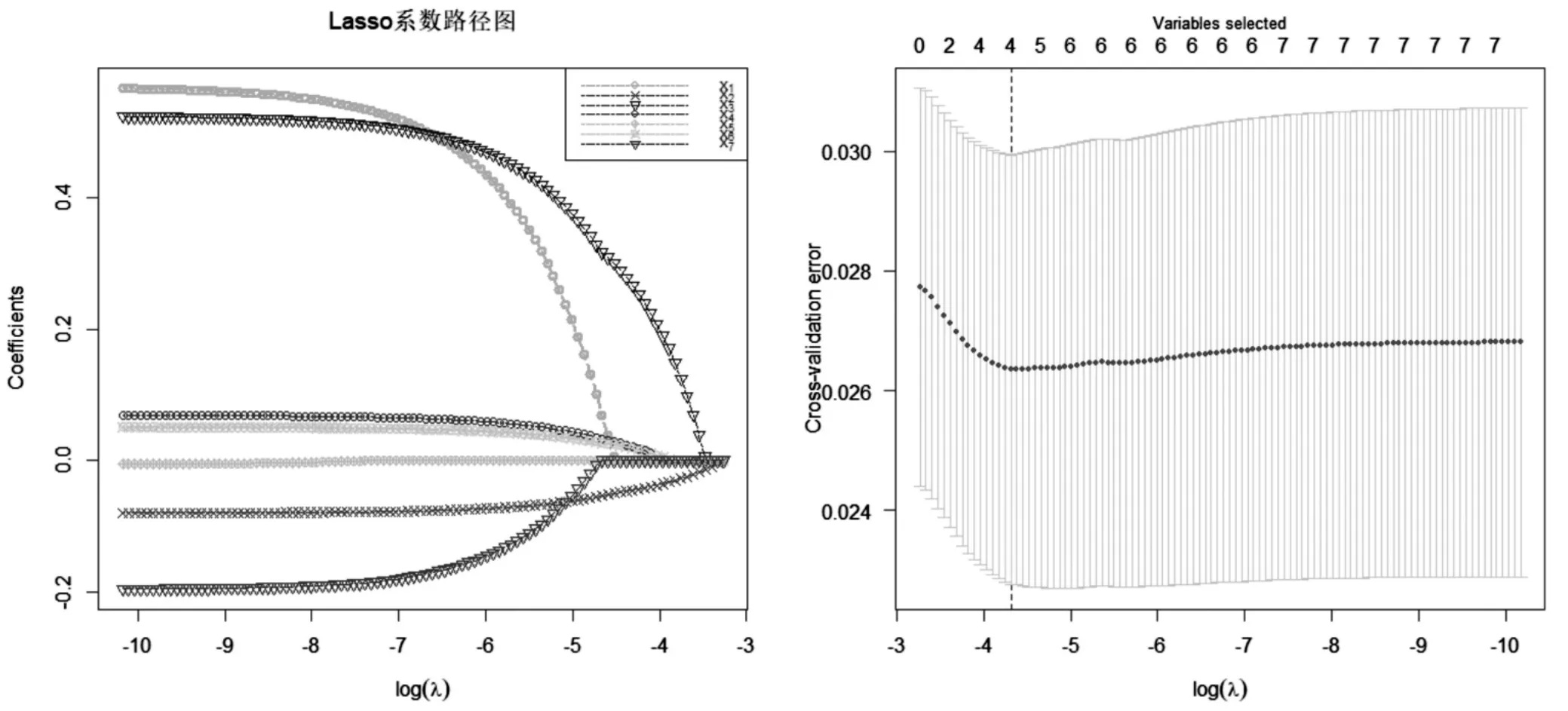
图1 Lasso变量选择的系数路径图和交叉验证图

从Lasso的系数路径图和交叉验证图可得到：λ的值是十折交叉验证确定的，随着log（λ）的增加，估计系数β变为0的变量越来越多；随着选取的指标数目不断增加，交叉验证的误差先下降后上升，当选取4个变量时，回归模型误差最小，约为0.026。

最终选择的变量为：高等院校师生比（x2）、教育经费投入（x3）、高技术产业从业人员数量（x4）、高新技术产业产值（x6）。

（三）数据来源

本文采用2011—2019年我国31个省、自治区、直辖市的面板数据作为研究对象。鉴于数据的可得性与全面性，本文使用的数据来源于国家统计局、各省（区市）的统计年鉴和《中国科技统计年鉴》。

四、区域创新能力的空间效应分析

为反映我国创新资源集聚情况，本文将创新要素指标面板数据运用到空间上，根据Lasso选择的4个变量，采用空间面板数据模型，将区域创新资源的溢出效应和空间相关性的作用机制更直观的显现。

（一）空间相关性分析

在进行空间计量模型设定前，先对研究的被解释变量做空间相关性检验，验证其是否存在空间上的自相关性。常用的自相关检验方法有Moran's I检验、LM检验、LR检验。因Moran's I检验具有很好的性质，渐进等价于LR检验、RS检验、LM检验，故本文选择最常用的Moran's I进行空间自相关检验，其计算公式如下：

j表示地区，取值为 1，2，…，31；i表示指标。Wij表示第j个地区的第i个指标的空间权重，采用0—1邻接矩阵法确定，即i和j相邻则取值为1，不相邻取值为0。且空间权重矩阵Wij对角线为0，同一地区永不相邻。

计算出Moran's I后，还要检验其显著性，看其是否具有显著性意义，检验方法为Z-score正态分布方法。如果Z-score正态分布方法通过了10%、5%或1%三个水平上的显著性检验，则说明Moran's I有显著意义，其公式如下：

本文使用距离权重矩阵，检验创新资源集聚变量的空间相关性。用stata15计算2011—2019年我国各省（区市）的创新能力Moran's I，结果如表2所示。

表2 2011—2019年创新能力全局Moran'sI

由表2可知，中国自2011年以来各省（区市）创新能力全局均大于0.1，且p值均通过显著性检验，表明我国31个省（区市）的创新能力水平有显著的空间正相关关系。为对区域创新能力空间集聚情况做进一步研究，本文绘制2019年31个省（区市）的创新能力Moran散点图，如图2所示。

图2 2019年创新能力Moran散点图

根据图2可分析得出我国31个省（区市）的创新能力空间聚集特征。位于第一象限表明该区域具有良好的空间溢出效应，对周边创新能力的发展起到一定的带动作用，位于第三象限表明该区域具有恶化的溢出效应，而位于第二、四象限则表明该区域与相邻区域之间不存在同方向的相互影响。江苏、山东、浙江、上海等具有高-高（H-H）聚集的空间特征特性；广西、河北、湖南位于第二象限，具有低-高（L-H）聚集的空间特性；大部分省（区市）位于第三象限，如四川、重庆、贵州、内蒙古、新疆等，具有低-低（L-L）聚集的空间特性；北京、广东位于第四象限，具有高-低（H-L）聚集的空间特性。

（二）空间计量模型设定与检验

1.模型设定

基于理论分析，可以构建出创新能力与各类创新资源投入的基本计量模型（见式5），由于指标的数据口径不统一，无法进行比较，因此取对数进行实证分析。

其中，被解释变量是区域创新能力（yit），以i区域t年的国内三种专利申请数量来表示。解释变量包括：高等院校师生比（x2）、教育经费投入（x3）、高技术产业从业人员数量（x4）、高技术产业产值（x6）。

同时，创新能力的空间相关性检验结果表明，区域创新能力具有明显的空间自相关性，基本计量模型与实际模型可能存在一定的偏差，故需要建立空间计量模型来进行区域创新能力分析，常用的空间计量模型有空间自回归（SAR）模型、空间误差（SEM）模型、空间杜宾（SDM）模型。

（1）加入被解释变量空间自回归项后，空间自回归（SAR）模型的形式如下：

ρ为区域创新能力的空间自相关系数，βi为回归系数，εi为随机误差项，且 εi～N（0，σ2In）。

（2）加入空间误差项，空间误差（SEM）模型的形式如下：

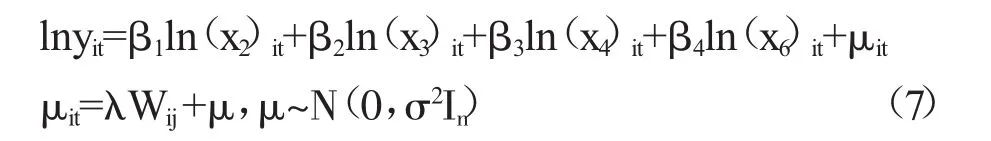
（3）在空间自回归（SAR）模型的基础上，加入解释变量的自回归项，得到空间杜宾（SDM）模型形式：

SDM模型可解释为三部分，第一部分：区域创新能力与相邻地区的创新能力有相关关系。第二部分：被解释变量和解释变量有相关关系，即创新能力与教育资源、人力资源和财力资源有关。第三部分：相邻区域的教育资源、人力资源和财力资源影响该区域的创新能力。

2.模型检验

首先，用LM检验对比SAR和SEM模型，从检验结果（表3）可以看出：SAR模型下的LM和Robust LM统计量的p值分别为0.941、0.135，SEM模型下LM和Robust LM统计量的p值均为0.000，只有空间误差模型才具有显著性，因此不适合选择空间杜宾模型进行分析，可选择空间误差（SEM）模型。

表3 LM检验结果

为进一步验证是否选择SEM模型，随后对空间杜宾（SDM）模型进行模型LR和Wald检验，检验结果如表4所示。

表4 SDM模型的LR和Wald检验

LR检验时p值为0.0149，测算结果显著，Wald检验的p值为0.2293，不具有显著性，说明空间杜宾模型会退化成SEM模型，再一次验证了本文适合用空间误差（SEM）模型来进行空间计量分析。

（三）空间计量模型结果分析

基于SEM模型，采用Hausman检验对模型的个体效应进行判定。用stata15对模型进行Hausman检验，得到卡方值为16.32，p值为0.0026，通过水平为5%的显著性检验，拒绝原假设，认为选择固定效应模型更适合SEM模型的分析。

故对式（7）进行模拟，得到SEM模型的空间固定效应模型、时间固定效应模型和双向固定效应模型的估计结果，如表5所示。

表5 SEM模型的效应系数

由表5可知，空间固定效应模型、时间固定效应模型和双向固定效应模型、随机效应模型的拟合优度的判定系数均高于0.7，模型的拟合优度较好。

其中，时间固定效应模型的可决系数最低，但变量的估计系数均在5%显著性水平下，通过显著性检验，四个变量的估计系数显著。其余模型均为0.82，但较多系数未通过显著性检验。因此，认为时间固定效应的SEM模型的计量结果比其余三个模型更适合用来解释变量的意义。空间误差（SEM）模型的系数在空间固定效应下为正，表明相邻省（区市）区域创新能力扰动误差对该地区创新能力有正向的影响，在时间固定效应下为负，表明时间对于该地区的创新能力有负向的影响。

因此，空间误差（SEM）模型的具体形式如下：

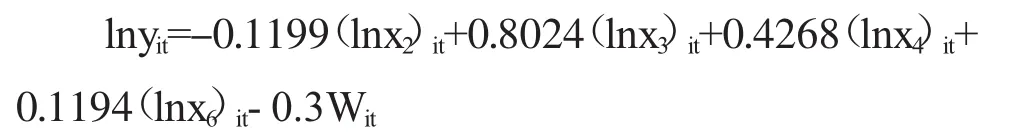
高等院校师生比在SEM模型的时间固定效应显著为负，高等院校师生比每上升1个百分点，区域创新能力就下降0.1199个百分点，区域师资力量的投入不足，高校学生和教师的不平衡对区域创新能力产生了明显的负影响作用。

教育经费投入、高技术产业从业人员数量、高技术产业产值系数估计在SEM模型的时间固定效应下都显著为正，分别为0.8024、0.4268、0.1194。教育经费投入每上升1个百分点，区域创新能力将增长约0.8024个百分点；高技术产业从业人员数量每增加1%，区域创新能力将增长0.4268%；高技术产业产值每提升1%，区域创新能力将增长0.1194%。说明教育资源、区域高技术产业的规模和经济效益对区域创新能力的影响起着十分重要的作用。

五、结论及建议

通过Lasso进行变量选择，在原有的指标中选择对创新能力有主要影响的4个变量，进行空间面板数据分析，得到以下结论：①区域创新能力有空间相关性且存在空间集聚现象。集聚效应呈现出中西部地区低低（L-L）集聚、东部沿海地区高高（H-H）集聚的两极分化、创新能力不均衡的态势。②构建SAR模型、SEM模型和SDM模型，通过LM检验、LR检验、Wald检验三大检验选择出SEM模型更适合本研究的实证分析；Hausman检验通过显著性检验，并对比空间固定效应、时间固定效应和双向固定效应，最终选定时间固定效应的SEM模型。③教育经费投入、高技术产业从业人员数量、高技术产业产值的投入对区域创新能力的提高有明显的正向促进作用，而高等院校师生比投入在空间维度上对区域创新能力有显著的负影响。

因此，为提高区域创新能力，在教育经费支持方面应加大力度，在高校本科生、研究生扩招的同时，也应当注重师资力量的引进，使其达到一个合理的平衡点，注重培养高质量人才。注重当地传统产业的升级转型，将传统制造业往高技术产业方向转型，紧跟国家创新发展潮流，注重新型基础设施建设、数字产业经济等新兴产业的发展。