傅里叶级数拟合LEO轨道误差下的BDS/GPS/LEO 精密单点定位

李相君，叶小舟，刘文祥，王飞雪

（ 国防科技大学 电子科学学院, 长沙 410073 ）

0 引 言

精密单点定位(PPP)技术只需要利用单台接收机接收伪距和载波相位观测值即可实现高精度定位，具有作业灵活、覆盖范围广、定位成本低、定位精度高等优点，已成为定位领域的热点和新发展方向[1].然而PPP技术也存在一定的短板，PPP所涉及的误差项与解算参数较多，处理过程较为复杂，导致其初始化时间较长[2]，而全球卫星导航系统 (GNSS)卫星轨道高度较高，信号传播到达地面时信号强度较弱，在边远地区和室内、森林等遮盖严重区域难以实现高精度连续可靠定位.

为了克服上述问题，国内外学者提出了利用低轨道地球卫星(LEO)播发导航信号来增强GNSS，从而实现GNSS/LEO联合PPP. 与GNSS相比，LEO星座轨道高度低，信号落地功率高，有助于改善边远地区定位性能. 其次，LEO运动速度快、几何构型变化明显，可以有效降低定位过程中观测方程间的相关性，增加参数的可估性，从而实现高精度快速定位[3-5].

马福建[6]全面评估了LEO星座卫星个数、轨道高度及轨道类型对PPP收敛时间的影响. 其结果表明：LEO星座卫星数目越多，PPP收敛时间越短. 以中纬度测站为例，引入60、96、192、288颗LEO后，PPP收敛时间分别从8.2 min减少至7.0 min、3.2 min、2.1 min、0.8 min. ZHAO等[7]建立了BDS/GPS/LEO三频非组合PPP模型，并设计了一个卫星个数为180颗的低轨星座. 其实验结果表明：与单BDS相比，BDS/GPS、BDS/LEO、BDS/GPS/LEO组合下的PPP浮点解精度分别提升42.77%、72.77%、77.73%.LI 等[8]建立GNSS/LEO三频组合观测量方程并分析了LEO星座对PPP模糊度解算的影响. 实验结果表明：LEO星座对PPP模糊度解算速度具有显著提升效果，且LEO数目越多，PPP模糊度固定速度越快.

上述仿真实验基本以获取LEO事后精密星历为前提进行PPP仿真实验，即假定LEO轨道误差很小，几乎忽略不计. 然而国内外的大多LEO星座设计目前仍然处在初步论证阶段，系统建设刚刚起步.LEO星座构型和轨道位置尚未确定，事后精密星历同样无法获取. 其次，实际PPP应用过程中对实时性要求较高，在进行PPP解算过程中主要采用精度较低的实时预报星历，必然会引入LEO轨道误差. 因此探究LEO轨道误差对GNSS/LEO联合PPP的影响十分重要.

柯明星等[9]将LEO轨道误差设定为服从零均值的正态分布，探究了不同轨道误差下LEO与GPS联合PPP的定位性能. 实验结果表明：当GPS轨道误差固定为0.25 m时，LEO轨道误差小于0.35 m，LEO与GPS联合PPP可以提升浮点解精度并缩短固定解的收敛时间. 当LEO轨道误差增加到0.4 m时，PPP浮点解精度将降低，固定解的收敛时间增加.

但是LEO轨道高度低，所处空间环境和受力情况较为复杂. LEO受到太阳活动，电磁活动等复杂外界因素影响以及大气阻力、辐射光压、重力场等模型误差影响，难以建立出LEO高精度确定性动力学模型[10]. 目前主要采用简化动力学定轨方法进行LEO精密定轨. 简化动力学定轨是在确定性动力学模型的基础上引入经验加速度模型来吸收未模型化的动力学误差，从而保证动力学模型对轨道的约束，并满足高精度定轨需求. 由于卫星轨道具有周期性，简化动力学定轨的经验加速度呈现准周期正弦曲线特点，简化动力学定轨后的LEO轨道误差也呈现准周期正弦曲线特点[11-12].

因此，本文根据LEO轨道误差特点，采用高阶傅里叶级数级数拟合LEO轨道误差，并由此探究LEO轨道误差对BDS/GPS/LEO联合PPP定位结果的影响.

1 BDS/GPS/LEO PPP模型

1.1 PPP函数模型

GNSS和LEO系统的伪距以及载波相位观测方程为：

式中：s、fs、r、i分别代表卫星、载波频率、接收机和历元；分别代表地面接收伪距与载波相位观测值；代表卫星发射天线相位中心到接收机天线相位中心的几何距离；ts,fs(i)、tr(i) 分别代表卫星和接收机钟差；分别代表卫星和接收机码硬件延迟偏差；分别为卫星和接收机相位硬件延迟偏差分别代表电离层延迟误差和对流层延迟误差； λfs代表fs对应的载波波长；代表整周模糊度； ϕs,fs为天线相位缠绕偏差为伪距和载波观测噪声.

在PPP处理过程中采用无电离层组合模型，利用观测方程的线性组合消除电离层一阶延迟量. 无电离层组合后的观测值的观测方程为：

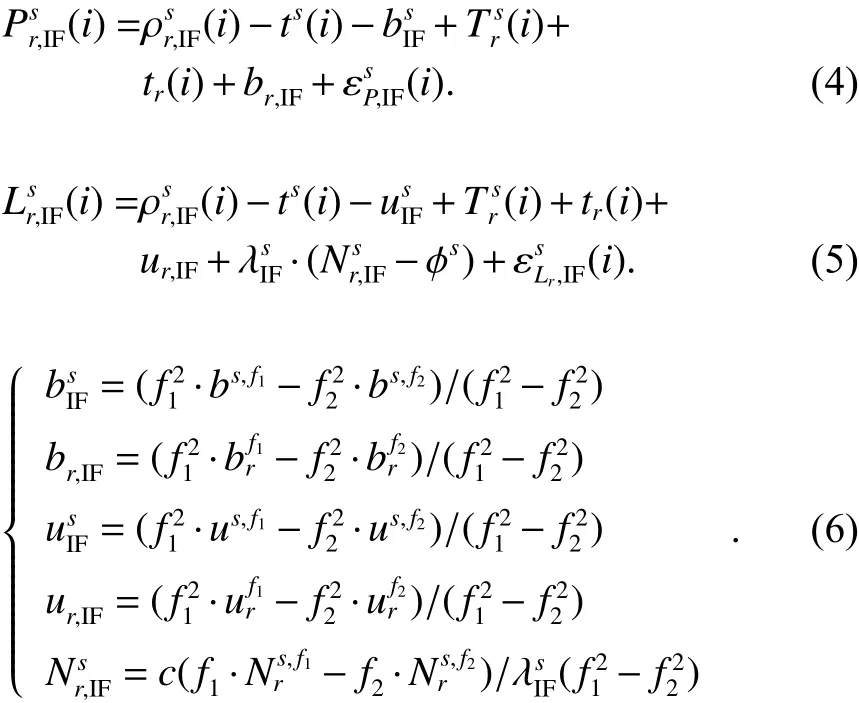
在PPP处理过程中，利用仿真星历产品消除部分轨道误差，精密钟差产品消除卫星钟差. 利用高精度修正模型和国际GNSS服务(IGS)产品修正对流层干分量延迟、天线PCV和PCO等，并将对流层湿分量作为未知参数进行估计. 将硬件码延迟作为接收机钟差的一部分，吸收到接收机钟差内. 并将UPD作为模糊度的一部分，吸收到模糊度内.

因此，无电离层组合模型下的伪距载波相位函数表达式可以简化为：

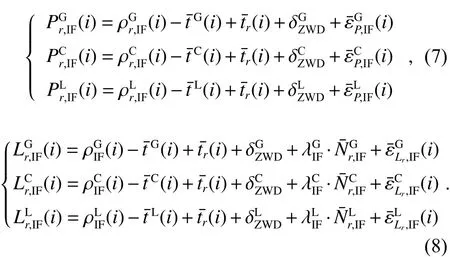
其中：G代表GPS，B代表BDS，L代表LEO星座.

因此，剩余的待估参数为接收机位置坐标，吸收了误差的接收机钟差，对流层湿分量延迟以及吸收了误差的模糊度参数.

1.2 PPP处理策略

表1 为BDS/GPS/LEO PPP处理策略.

表1 BDS/GPS/LEO PPP处理策略

2 实验数据仿真

2.1 BDS、GPS、LEO星座构型仿真

本文星座构型和卫星轨道位置均利用STK航空商业仿真软件进行设计以及仿真. STK仿真时间环境配置为2021-05-01T00:00:00—2021-01-02T00:00:00.场景仿真时长为1天. BDS、GPS和LEO星座构型仿真参数如表2所示.

表2 仿真星座构型参数

2.2 LEO地面接收数据仿真

LEO地面接受数据仿真是在计算卫星接收机真实距离后增添各项误差和观测噪声所得[14].

首先，设定LEO星座系统信号载频为B1、B2频率. 利用STK软件以30 s的采样间隔输出卫星在ECEF坐标系下的三维坐标以及三维速度矢量，进行卫星位置与卫星运行速度仿真. 然后获取IGS和iGMAS提供的仿真当日GPS与北斗三号(BDS-3)精密钟差产品. 并将其等效成LEO精密钟差产品，进行卫星精密钟差仿真. 并运用迭代法计算卫星发射时刻位置，再利用行星列表计算仿真固体潮误差数值；利用BLQ文件仿真得到海潮误差；利用地球自转参数ERP文件计算极潮. 然后运用ATX产品仿真得到卫星端与接收机天线端PCV与PCO[15]. 考虑相对论效应，根据式(3)计算得到基于GIM模型计算电子浓度总含量(TEC)，并根据高度选取合适的比例系数来计算电离层延迟[16]. 再采用Hopfiled模型进行干分量延迟建模仿真，将实测国际GNSS服务(IGS)数据进行PPP解算，求得对流层湿延迟分量，将解算结果等效到本实验仿真[17]. 利用实测IGS数据进行PPP解算求得接收机钟差仿真. 且为保证仿真的真实性，同样采用实测数据仿真法，利用真实IGS数据进行PPP解算，得到真实路径高度角与之对应的残差值. 再计算仿真路径高度角，选取仿真高度角与真实路径高度角最相近的路径进行伪距与载波相位多路径残差仿真. 最后仿真出白噪声形式的伪距载波量测噪声，模糊度与伪距硬件延迟可进行人为随机设定. 通过观测方程，计算得到地面接收数据.

2.3 傅里叶级数拟合轨道误差

由于简化动力学需要引入额外的经验摄动力模型来吸收摄动力模型误差和未模型化的误差，且简化动力学定轨法的经验加速度呈现准周期正弦特性[10].因此卫星轨道误差同样呈现准周期正弦特性，

LEO轨道误差函数模型可有傅里叶级数表示为

式中：e(t) 表 示LEO轨道误差；n表示傅里叶级数的阶数；c表示常数项；ai、bi分 别为傅里叶展开系数； ω 表示基频；t表示时间.

不同时空环境条件下动力学模型和不同外部星历产品改正后定轨误差基本不会相同，因此对拟合弧段内的轨道误差的变化规律，只需要从趋势上进行拟合，无需在其幅度上进行拟合.

在仿真过程中，首先设定LEO轨道误差均方根(RMS)为R0，选取傅里叶展开系数初值并计算LEO轨道误差RMS为R，若满足

则说明仿真误差符合设定需求，否则逐渐增大傅里叶展开级数，不断迭代计算得到R，直至达到上述条件.

以RMS=0 cm、2 cm、5 cm、10 cm、20 cm、30 cm的LEO轨道误差为例，利用傅里叶级数拟合法进行LEO轨道误差拟合. 其径向、法相、切向的误差形式如图1所示.

图1 傅里叶级数拟合LEO轨道误差图

3 仿真实验分析

本文定义LEO星座轨道数为N，每个卫星轨道面的卫星个数为M. 在表示LEO星座构型时通过N×M来进行表述.N×MLEO 星座表示为轨道数目为N，每个卫星轨道面的卫星个数为M的LEO星座.并定义静态PPP收敛时间为定位结果东(E)、北(N)和天顶(U)方向的误差均小于并在此之后始终小于5 cm时所需要的时间.

3.1 不同LEO轨道误差下的BDS/GPS/LEO PPP定位精度

本小节中PPP仿真时长为1天，观测值PPP解算时间间隔为30 s. PPP定位精度定义为最后500个历元PPP解算出的定位误差RMS. 以中纬度地区测站JFNG为例，通过设定LEO轨道误差RMS=0 cm、2 cm、5 cm、10 cm、20 cm、30 cm，仿真计算出在6×10LEO 星座下的BDS/GPS/LEO PPP精度.

由图2可知，仿真时长在1天范围内，LEO轨道误差RMS从0 cm逐渐增加到30 cm时，BDS/GPS/LEO PPP定位精度均能达到收敛条件，不会出现定位不收敛情况.

图2 不同LEO轨道误差下的JFNG测站PPP精度图

采用相同处理方法，选取高中低纬度地区多个测站进行蒙特卡罗仿真，计算高中低纬度测站的PPP平均定位误差.

表3 和图3表示高、中、低纬度测站在LEO轨道误差RMS=0 cm、2 cm、5 cm、10 cm、20 cm、30 cm下的BDS/GPS/LEO PPP定位精度. 可以发现，在LEO轨道误差RMS相同的条件下，高、中、低纬度测站的PPP定位误差基本一致，相差在1.5 cm以内，造成偏差的主要原因为LEO轨道误差的随机性和蒙特卡罗仿真次数的有限性. 但LEO轨道误差RMS增加到2 cm、5 cm、10 cm、20 cm、30 cm时，定位误差增加至0.26 cm、0.33 cm、0.65 cm、0.90 cm、1.92 cm、3.05 cm. 因此，PPP定位误差与测站纬度无明显关系，但随着LEO轨道误差的增加而逐渐增加.

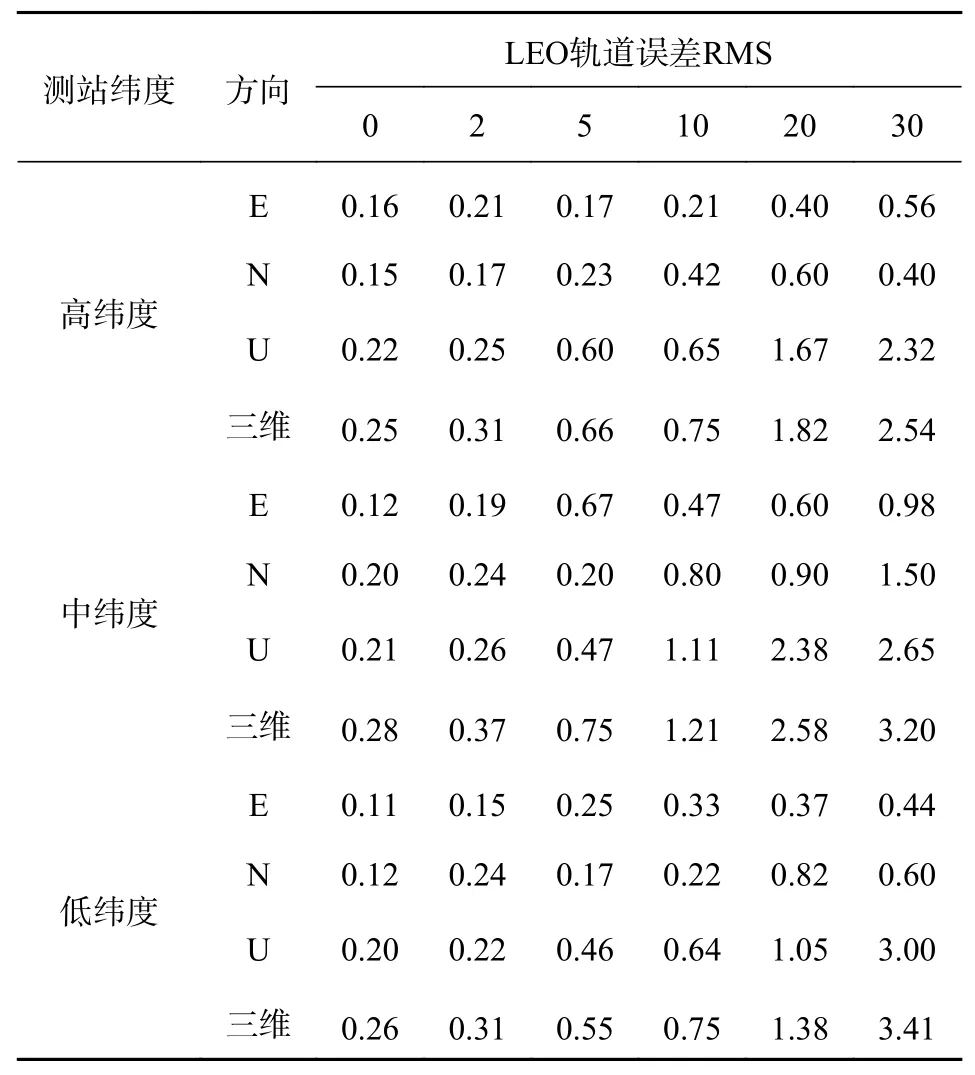
表3 不同LEO轨道误差下高中低纬度测站PPP精度 cm

图3 不同LEO轨道误差下高、中、低纬度地区PPP精度

为比较不同LEO星座构型下的BDS/GPS/LEO PPP定位精度，同样以中纬度地区测站JFNG为例，仿真计算出引入12×10 LEO 星座和18×10 LEO星座后，LEO轨道误差RMS=0 cm、2 cm、5 cm、10 cm、20 cm、30 cm时的BDS/GPS/LEO PPP定位精度.

表4 和图4表示6×10、12×10、18×10 LEO星座下，LEO轨道误差RMS=0 cm、2 cm、5 cm、10 cm、20 cm、30 cm时的BDS/GPS/LEO PPP定位精度. 可以发现在LEO轨道误差RMS相同的条件下，不同的LEO星座构型下的BDS/GPS/LEO PPP定位误差基本一致，偏差在1.5 cm以内，造成偏差的主要原因为LEO轨道误差RMS的随机性和蒙特卡罗仿真次数的有限性.

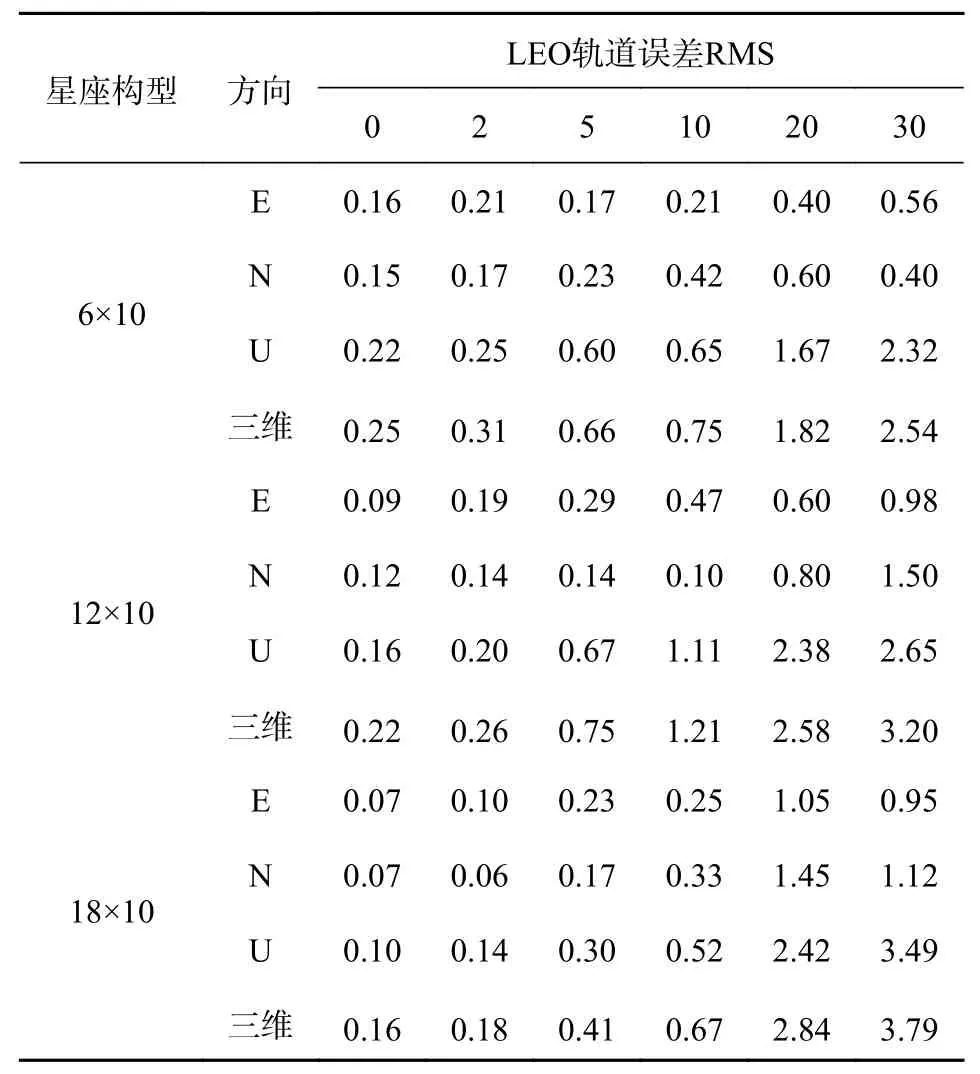
表4 不同下高中低纬度测站PPP精度 cm

图4 不同LEO轨道误差和星座构型下的PPP精度

因此，在相同LEO轨道误差下的BDS/GPS/LEO PPP定位误差与测站纬度以及LEO星座构型和LEO数目均关联不大，且只随着LEO轨道误差的增加逐渐增大.

3.2 不同LEO轨道误差下的BDS/GPS/LEO PPP收敛时间

为精确计算BDS/GPS PPP收敛时间和不同LEO轨道误差下BDS/GPS/LEO PPP的收敛时间，本小节中PPP仿真间隔为1 h，观测值PPP解算时间间隔为2 s.

以中纬度地区测站JFNG为例，通过设定LEO轨道误差，仿真在6×10 LEO星座下的BDS/GPS/LEO PPP.

由图5可知，当引入LEO星座后，BDS/GPS/LEO PPP 收敛时间与BDS/GPS PPP收敛时间相比，有明显的缩短. 但当引入LEO轨道误差RMS后，BDS/GPS/LEO PPP 收敛时间会随着LEO轨道误差的增加而逐渐增大，直到达到并超过BDS/GPS PPP收敛时间. 说明此时引入LEO星座并不能改善PPP收敛性能，反而因为LEO轨道误差RMS的引入恶化了PPP的收敛性能.利用相同仿真方法，计算出高、中、低纬度测站在引入6×10、12×10、18×10 LEO后，不同LEO轨道误差下不同纬度测站的BDS/GPS/LEO PPP收敛时间.由图6可知，在相同LEO星座构型下，高、中、低纬度测站PPP收敛时间均随着LEO轨道误差RMS的增加而逐渐增大. 在相同LEO轨道误差RMS的条件下，随着LEO星座卫星数目的增加，高、中、低纬度测站PPP收敛时间逐渐减小. 由于LEO星座为极轨星座，其LEO可见卫星数目随着纬度的增加而增加. 因此引入LEO星座后，高纬度测站PPP收敛时间始终最小，中纬度测站次之，低纬度测站PPP收敛时间最长. 但随着引入的LEO星座卫星数目的逐渐增多，相同LEO轨道误差RMS下，高、低、中纬度测站PPP收敛时间差距逐渐减小.

定义每增加1 cm的LEO轨道误差RMS的条件下，PPP收敛时间平均增加数值为收敛时间变化率kLa,Sa. 其数学表达式为：

式中：La表示测站纬度；Sa表示LEO星座构型；t表示收敛时间；m表示LEO轨道误差. 其不同纬度不同星座构型的kLa,Sa如表5所示：

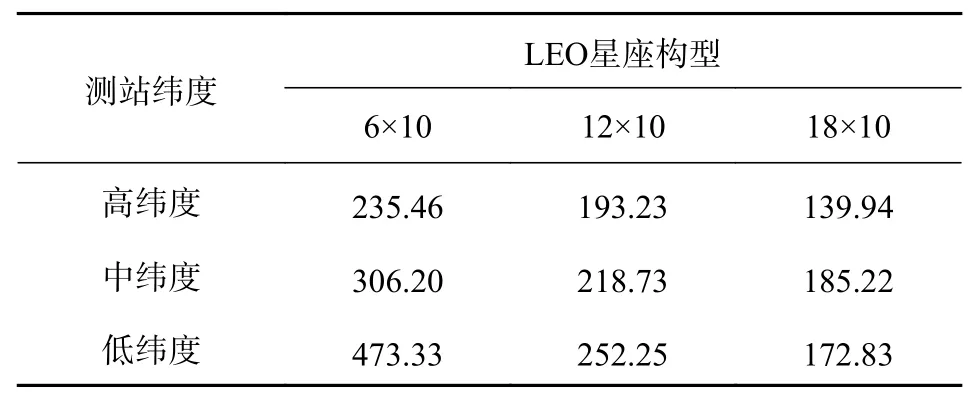
表5 PPP收敛时间变化率 (s·cm-1)

由表5可知，高中低纬度测站下的kLa,Sa随着LEO数目的增加而逐渐降低，说明LEO轨道误差对PPP收敛时间影响作用随着LEO数目的增加而逐渐降低. 即LEO数目越多，PPP收敛时间对LEO轨道误差“容忍性”越好.

仿真计算出高、中、低纬度测站不引入LEO时BDS/LEO PPP收敛时间以便于与不同LEO轨道误差下BDS/GPS/LEO PPP的收敛时间进行比较，结果如表6所示.

表6 高中低纬度测站BDS/GPS PPP收敛时间 s

如图7所示，在相同LEO轨道误差下，随着LEO星座卫星数目的增加，低纬度测站PPP收敛时间缩短效果最为明显，中纬度次之，高纬度测站PPP收敛时间缩短效果最差. 其主要原因为引入LEO星座后，高纬度测站PPP收敛时间极具缩短，在逐渐增加LEO数目后，PPP收敛性能提升效果已经不太明显. 引入6×10 LEO星座后，为了使高、中、低纬度测站BDS/GPS/LEO PPP收敛时间小于BDS/GPS PPP收敛时间，LEO轨道误差应小于9 cm、7 cm、5 cm；引入12×10 LEO星座后，为了使高、中、低纬度测站BDS/GPS/LEO PPP收敛时间小于BDS/GPS PPP收敛时间，LEO轨道误差应小于12 cm、11 cm、12 cm；引入18×10 LEO星座后，为了使高、中、低纬度测站BDS/GPS/LEO PPP收敛时间小于BDS/GPS PPP收敛时间，LEO轨道误差应小于12 cm、14 cm、17 cm.

因此，为保证全球区域BDS/GPS/PPP收敛时间均优短于BDS/BDS PPP收敛时间，引入6×10、12×10、18×10 LEO星座后，LEO轨道误差应小于5 cm、11 cm、12 cm. 且由于高纬度地区收敛时间提升效果已经达到极限，不会再随着LEO数目的增加而明显改善. 因此继续增加LEO数目，LEO轨道误差均应小于12 cm以保证全球区域BDS/GPS/PPP收敛时间均短于BDS/BDS PPP收敛时间.

4 结束语

本文提出了一种傅里叶级数拟合LEO轨道误差下的BDS/GPS/LEO PPP分析方法. 仿真分析了利用傅里叶级数拟合的LEO轨道误差对BDS/GPS/LEO PPP定位精度和收敛时间的影响，得到了以下结论：

1) 在LEO轨道误差相同的条件下，不同LEO星座构型，不同纬度测站的BDS/GPS/LEO PPP定位误差基本一致. 但BDS/GPS/LEO PPP定位误差随着LEO轨道误差的增加而逐渐增大.

2) 在相同LEO星座构型下，不同纬度测站PPP收敛时间均随着LEO卫星轨道误差的增加而逐渐增大.

3) LEO轨道误差对PPP收敛时间影响的变化率均随着LEO数目的增加而逐渐减小，LEO轨道误差对PPP收敛时间影响作用随着LEO数目的增加而逐渐降低.

4) 为保证全球区域BDS/GPS/PPP收敛时间均短于BDS/GPS PPP收敛时间，引入6×10、12×10、18×10 LEO星座后，LEO轨道误差RMS应小于5 cm、11 cm、12cm. 且由于高纬度地区收敛时间提升效果已经基本达到极限，不会再随着LEO数目的增加而明显改善. 因此继续增加LEO数目，其LEO轨道误差均应小于12 cm，以保证全球区域BDS/GPS/PPP收敛时间均短于BDS/BDS PPP收敛时间.