重力场模型对Swarm卫星精密定轨的影响分析

方文豪，孔巧丽，李长松，张德志，张令纲，王田发

（ 山东科技大学 测绘与空间信息学院, 山东 青岛 266590 ）

0 引 言

欧洲航天局(ESA)已于2013年11月22日成功发射Swarm卫星[1]，Swarm星座是ESA首个用于测量来自地球核心、地幔、地壳、海洋、电离层等区域磁场信息的对地观测卫星星座[2]. 该星座包括A、B、C三颗小卫星，分别运行在2个轨道面上. 其中Swarm-A和Swarm-C卫星在高度450 m，倾角87.4°的极轨道面运行，而Swarm-B卫星在高度530 m，倾角88°的极轨道面飞行[3].

自星载GPS观测技术成功应用于TOPEX/Poseidon卫星[4]以来，该技术已成为低轨卫星精密定轨最主要的技术手段. 常见的低轨卫星精密定轨方法有动力学定轨、简化动力学定轨以及运动学定轨. 采用动力学法能够获得连续的卫星轨道坐标及速度，但难以精确测定大气阻力、太阳光压以及地球返照射压等摄动力，因此卫星的定轨精度有待进一步提高[5].运动学法利用星载GPS双频观测值对低轨卫星进行精密定轨，不考虑低轨卫星的受力情况和天气状况，精度不受低轨卫星轨道高度的影响[6]. 但这种方法的定轨精度与GPS卫星的几何图形结构有很大关系，因此，其定轨精度并不稳定[7]. 简化动力学法融合了动力学法和运动学法的优点，采用过程附加参数来吸收动力学模型误差与未被模型化的误差，通过确定几何信息与动力学模型之间的最优权来减弱动力学模型对精度的影响，从而实现几何信息和动力学信息的最佳匹配[8-9]. 随着星载GPS测轨技术的迅速发展，利用简化动力学法进行低轨卫星精密定轨获得了广泛的应用. 文献[7]采用星载GPS观测数据，对Swarm卫星进行精密定轨，定轨精度为4～7 m. 文献[10-11]采用简化动力学法对GOCE卫星进行精密定轨，轨道精度优于2 m. 文献[12]利用星载GPS双频观测值，对GRACE卫星进行简化动力学定轨，GRACEA与GRACE-B的轨道精度均达到2.5 m. 文献[13]将简化动力学定轨应用于TOPEX/Poseidon卫星，其定轨精度优于3 m. 文献[14]利用BERNESE5.2对Jason-3卫星进行精密定轨，精度优于3.6 m. 文献[15]运用简化动力学法对HY-2A卫星进行精密定轨，其径向定轨精度达到2 m.

在对Swarm卫星进行简化动力学定轨过程中，卫星所受到的摄动力模型会影响其定轨精度，其中地球重力场模型的精度对定轨精度的高低具有较大的影响. 不同的地球重力场模型和不同阶次的重力场模型会对卫星定轨精度产生不同的影响. 本文利用Swarm卫星星载GPS双频观测值和简化动力学法，对Swarm卫星精密轨道进行解算. 解算轨道的过程中引入适当的伪随机脉冲参数，并将这些参数与其他参数一起估计. 重点研究了GOCO06s地球重力场模型展开到不同阶次时的Swarm卫星简化动力学定轨精度，并且探讨了采用100阶次的PGM2000a、EIGEN-2、EGM2008和GECO重力场模型对Swarm卫星轨道的影响，得出了一些有益的结论.

1 简化动力学定轨理论

简化动力学定轨方法是低轨卫星精密定轨的常用方法. 该方法能够充分利用星载GNSS观测数据和动力学模型的优点实现低轨卫星的精密定轨. 为了减少待求参数的个数，一般会引入经验参数或伪随机脉冲参数，从而吸收动力学模型误差和未被模型化的摄动力误差. 该方法可以保证动力学模型对卫星轨道的约束，从而有效提高低轨卫星精密定轨精度[16].

低轨卫星在轨道上运行时会受到多种摄动力的作用，从而导致卫星轨道比较复杂. 这些摄动力包括地球非球形摄动、地球潮汐摄动、相对论效应、多体摄动等保守摄动力和大气阻力、太阳光压、地球返照压等非保守摄动力. 在惯性系中，低轨卫星运动方程表示为[5]

2 数据来源和处理策略

本文采用欧空局(ESA)提供的1 s采样间隔的星载GPS双频观测数据，欧洲定轨中心(CODE)提供的15 min采样间隔的GPS卫星精密星历文件、地球自转参数文件和30 s采样间隔的精密卫星钟差文件. 观测数据的时间跨度为2020-08-01—05，采用的软件为BERNESE5.2. 伪随机脉冲和分段常数加速度的时间间隔均设置为6 min，伪随机脉冲先验标准差设置为10-6m/s，分段常数加速度先验标准差设置为10-9m/s. 基于简化动力学定轨法，利用最小二乘法将伪随机脉冲参数和其他轨道参数一起进行解算，从而得到卫星精密轨道. 表1为Swarm卫星简化动力学定轨模型及处理策略.

表1 Swarm卫星简化动力学定轨模型及处理策略

3 Swarm卫星定轨结果分析

采用外符合法进行轨道精度验证，参考轨道为ESA提供的科学轨道. 为了分析不同阶次的GOCO06s地球重力场模型对Swarm系列卫星定轨精度的影响，本文将GOCO06s地球重力场模型分别展开到30阶、50阶、80阶、100阶及120阶，利用BERNESE5.2软件基于简化动力学方法采用上述不同阶次的重力场模型解算Swarm卫星精密轨道. 表2为定轨精度统计信息，采用30、100及120阶次GOCO06s地球重力场模型解算的Swarm-A、Swarm-B和Swarm-C卫星的简化动力学轨道与参考轨道差异分别如图1～3所示.

图1 采用30阶次GOCO06s地球重力场模型解算的轨道与参考轨道差异

表2 采用不同阶次的GOCO06s地球重力场模型解算的卫星轨道与参考轨道差值 m

图2 采用80阶次GOCO06s地球重力场模型解算的卫星轨道与参考轨道差异

由图1～3和表2可知：采用30阶次的GOCO06s地球重力场模型解算的Swarm卫星轨道精度均保持在分米级，无法满足低轨卫星精密定轨的需求. 当GOCO06s地球重力场模型的阶次保持在30～100阶次时，随着重力场阶次的不断增加，Swarm-A、Swarm-B和Swarm-C卫星在径向、切向、法向上的定轨精度越来越高，而在100阶次与120阶次的定轨精度相当，说明在100阶次定轨精度基本稳定. 采用120阶次的GOCO06s地球重力场模型进行简化动力学定轨，Swarm-A卫星的径向、切向、法向以及三维方向上的定轨精度分别为0.009 m、0.018 m、0.014 m和0.024 2 m，Swarm-B卫星的定轨精度分别为0.009 m、0.016 m、0.013 m和0.023 m，Swarm-C卫星的定轨精度分别为0.008 m、0.016 m、0.015 m和0.024 m. 因此可以看出，三颗Swarm卫星的定轨精度均优于3 cm.

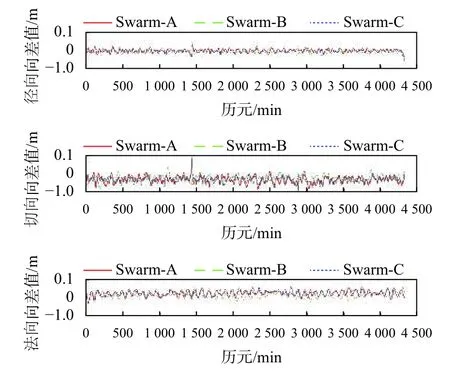
图3 采用120阶次GOCO06s地球重力场模型解算的卫星轨道与参考轨道差异

此外，采用100阶次的PGM2000a、EIGEN-2、EGM2008以及GECO重力场模型分别对Swarm卫星进行定轨，以此来考察不同的地球重力场模型对Swarm卫星定轨精度的影响. 分别采用100阶次的各重力场模型对Swarm-A、Swarm-B和Swarm-C卫星进行精密定轨，定轨结果与参考轨道差值的均方根(RMS)统计信息见表3.

表3 100阶次的不同重力场模型解算的Swarm卫星定轨结果与参考轨道差值RMS m

由表3可知，利用100阶次的PGM2000a重力场解算出的三颗Swarm卫星轨道精度均在分米量级，而采用100阶次的EIGEN-2、EGM2008以及GECO重力场模型得到的轨道精度均在厘米量级，定轨精度优于3 cm. 由此可以看出，采用EIGEN-2、EGM2008以及GECO重力场模型得到的定轨精度明显均优于PGM2000a. 由表2和3可知，相比于100阶次的PGM2000a、EIGEN-2、EGM2008以及GECO重力场模型，采用100阶次的GOCO06s、GECO和EGM2008模型解算出的Swarm卫星轨道精度相对较高. 所以，为了保证解算出的Swarm卫星轨道具有较高的精度和稳定性，实际解算卫星轨道时，需要考虑卫星的在轨运行高度等情况，合理选取地球重力场模型及其阶数.

4 结束语

本文采用星载GPS双频观测数据对Swarm卫星进行简化动力学定轨，在轨道解算过程中加入伪随机脉冲参数. 详细研究了GOCO06s地球重力场模型分别展开到30阶、50阶、80阶、100阶以及120阶时的Swarm卫星简化动力学定轨精度，对比了采用100阶次的PGM2000a、EIGEN-2、EGM2008以及GECO重力场模型时解算的Swarm卫星轨道精度，得到结论如下：

1)当GOCO06s地球重力场模型从30阶次逐步展开到100阶次时，解算出的Swarm-A、Swarm-B和Swarm-C卫星轨道在径向、切向、法向上的精度越来越高，在重力场模型阶次大于100时，轨道精度稳定，3颗卫星的精度均优于3 cm.

2)采用100阶次的PGM2000a重力场模型解算出的卫星定轨精度在分米量级，而利用同阶次的EIGEN-2、EGM2008以及GECO重力场模型解算的轨道精度均保持在厘米级，其中采用GECO和EGM2008模型解算出的轨道精度与GOCO06s解算出的轨道精度相当.

3)实际解算卫星轨道时，为了得到较高的定轨精度，需要合理选取地球重力场模型及其阶次.