GNSS调零抗干扰天线的反欺骗性能分析

任彬彬，倪少杰，陈飞强，吴健，高立朝

（ 1. 国防科技大学 电子科学学院, 长沙 410073；2. 北京遥测技术研究所, 北京 100076 ）

0 引 言

随着卫星导航技术的迅速发展，卫星导航系统已逐步从军事领域扩展到民用领域、渗透至国民经济各个部门，成为国家定位、导航和授时(PNT)体系的重要组成部分[1]. 导航战(NAVWAR)理念的提出[2]，对卫星导航系统干扰与抗干扰技术的研究正受到越来越多的关注，其中利用天线阵的空域抗干扰是目前最有效的干扰抑制技术[3].

天线阵抑制干扰的基本原理是自适应调整天线阵的方向图，使其在干扰来向形成零陷，对干扰的功率进行衰减. 许多研究都提出了几种有效的全球卫星导航系统(GNSS)阵列自适应算法[4-7]. 对于导航接收机，功率倒置(PI)算法是应用相当广泛的空域抗干扰算法[8-12].

PI算法利用自适应调零天线接收信号，根据信号的强度自适应调整天线阵的权系数，在干扰信号对应的方向形成零陷. 其优势是不需要知道期望信号的先验信息，实现简单. 在雷达、扩频通信等强干扰、弱信号的环境中得到了广泛应用[13-14].

目前国内外关于PI算法在各种环境下的性能分析较为全面，COMPTON[9]阐述了PI的概念，对PI算法天线阵列进行性能的分析与研究. MYRICK等[15]阐述了GPS系统的自适应算法，选取PI算法实现准则. GECAN等[10]研究了采用最小二乘算法的GPS接收机的PI天线阵列的性能. 田玉坤等[16]利用最小二乘算法迭代计算PI的最优权值，针对四阵元天线仿真了PI算法在不同干扰条件下的抗干扰性能，以及迭代步长等因素对算法收敛性能的影响. 桑怀胜等[17-18]仿真分析了采用RLS算法实现PI阵列的性能. 石荣等[19]分析基于线性约束最小准则(LCMV)下求得的PI最优权矢量和基于最小二乘算法的PI最优权矢量是相等的，两种PI模型完全等效.

需要指出，对PI算法的分析都是在干扰功率高于噪声水平的前提下进行的，并且大部分分析都集中在寻找最优权向量的计算方案上[20-23]. 关于抗欺骗性能的分析很少，欺骗信号功率一般高于真实信号功率0～40 dB，大部分的欺骗信号功率是低于噪声水平的. 主要关注的指标是输出的信号与干扰加噪声比(SINR)，但是在导航系统中，真实信号功率远远低于噪声水平，SINR的变化范围非常小，所以这个指标并不适用于本文的研究.

因此本文对导航系统中欺骗信号对PI性能的影响进行了研究分析，主要针对输出的欺骗信号和真实信号功率、载噪比，以及欺骗抑制比等导航领域常用的指标. 通过研究推导，得到如下结论：当天线阵输入的欺骗信号逐渐增加时，输出的真实信号功率几乎保持不变，而输出的欺骗信号功率先增加后减小. 并通过仿真和实测验证了结论的正确性.

1 问题提出

1.1 信号模型

考虑一个天线阵阵元数为N，假设有q个导航信号源从不同的角度 θ1,θ2,···,θq入射到该天线阵，其中信号和噪声相互独立，期望信号来向已知为 θ1，其余信号计为欺骗信号，则天线阵接收的N路信号可以写成表达式

v(t)是欺骗加噪声矢量，其表达式为

式中：si(t) 表 示在阵列参考点接收的第i个信号；n(t)是具有0均值和协方差矩阵 σnI的高斯随机向量；α(θi)表示对应信号的导向矢量，各个导向矢量的重要性质为

为使公式简洁，下文中使用 αi来 代替 α (θi) .

1.2 在有限快拍数下权矢量的表达形式

PI准则是以某一个阵元的输出作为参考信号，保证这一路信号输出功率的加权系数恒定，调整其他通道的阵列取值，使阵列输出信号的功率最小，其优化目标可以表达为[24]

式中：c1为除第一个元素为1外其余元素均为0的N维列矢量，等价于固定第一个阵元的权值为1，调整 [w1,w2,···wN]H

使输出功率最小，约束的目的是为了避免得到无意义的全零解，即w1=w2=···=wN=0 ，对上式进行求解，可得PI算法最优权值的表达式为

式中，Rx=E[x(t)xH(t)] 表示阵列接收数据的协方差矩阵.

在快拍数有限的情况下，PI算法实际的权矢量应表示为

rˆ 为期望信号和欺骗加噪声信号的采样互相关

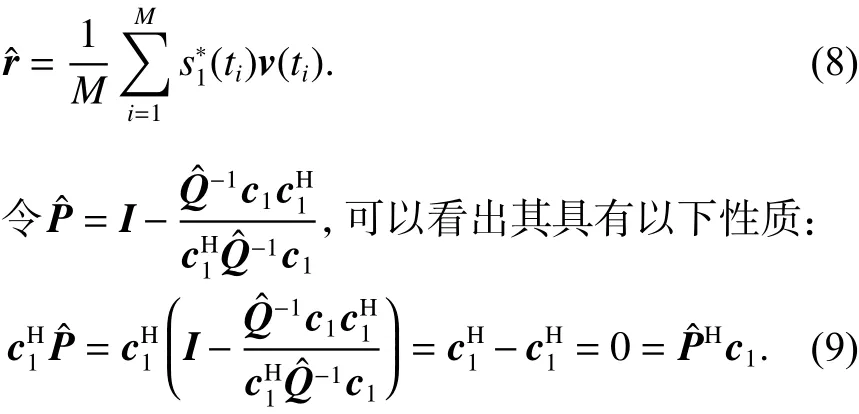
上式说明了在有限快拍数下权矢量可以分为两部分：只由欺骗和噪声决定的权值部分权矢量部分(式右边第一项)和由欺骗信号和期望信号的相关性以及有限快拍数引起的非期望扰动部分(式右边第二项).

2 欺骗信号功率对算法性能影响

经过PI算法处理后的阵列信号可以写成如下形式

为了简化运算，本文只考虑存在单个欺骗信号的情况，即

将式(12)代入式(11)得到

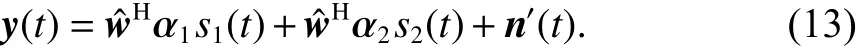
式中，n′(t)=wˆHn(t) ，是天线阵输出的噪声.

此时

为了分析输入欺骗信号的功率对PI算法影响，本文分别研究了其对期望信号以及欺骗信号输出功率的影响.

2.1 期望信号输入功率对期望信号输出功率影响

期望信号输出功率表达式为

将式(6)～(8)代入式(18)中，Ps又可以表示为

由式(20)可知，输出期望信号的功率与多个输入变量有关，首先是期望信号和欺骗信号的输入功率，其次是天线阵的阵型以及两种信号在时域和空域上的相关性[25]，是一个复杂的多元函数.

2.2 欺骗信号输入功率对欺骗信号输出功率影响

经由天线阵加权处理后的欺骗信号功率可以表示为

将式(22)化简得

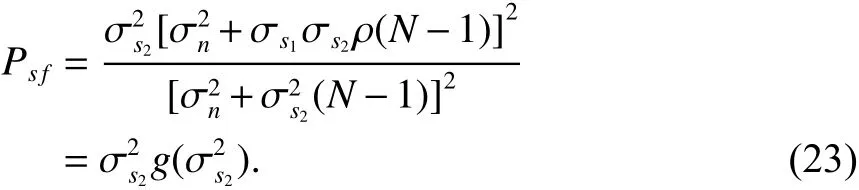
看出欺骗信号输出功率受真实信号和欺骗信号输入功率以及噪声功率和阵元数的影响.

由于噪声带宽为20 MHz时，导航信号通常比噪声低30 dB[26]，欺骗信号一般高于真实信号0～40 dB，因此当欺信比(欺骗信号功率比真实信号功率)较低时，即欺骗信号和真实信号功率相差不大时，有此时原式可以化简为

可以很直观看出，在欺信比较小时，输出欺骗信号功率大致等于输入欺骗信号功率，即PI算法此时不对欺骗信号进行抑制.

3 仿真结果分析

为了验证上节的分析结果并更深入地了解PI算法的抗欺骗性能，本文在这一节用仿真结果和理论分析进行比较. 使用200次蒙特卡洛运行的样本均值代替期望算子，每次运行由1 500个数据样本组成，一共设置了两组仿真场景.

3.1 场景1

仿真场景设置，天线阵为7元中心圆阵，阵元间距为0.5 λ ，图1为阵元排布情况.

图1 阵元排列示意图

仿真场景1中信号设置如下：期望信号到达角(俯仰角，方位角)为[70°，120°]，功率为-160 dBw；欺骗信号到达角为[10°，10°]，由于欺骗信号功率通常在噪声水平之下，在本文仿真中令其功率从-160～-110 dBw递增，在仿真中统一使用欺信比来表征欺骗信号的功率，即欺信比在0～50 dB；噪声的功率谱密度为-205 dBw/Hz，接收机带宽为20 MHz. 欺骗信号比期望信号延迟1个码片.

在上述信号设置下，计算得到相关系数为ρ=0.007-0.009i，真实信号和欺骗信号的导向矢量α1、α2以及二者的空间相关系数 α 为：

在实验中，首先仿真了真实信号和欺骗信号输出功率随着欺信比的变化，欺信比从0以1 dB为间隔逐渐递增到50 dB，图2～3为仿真结果.

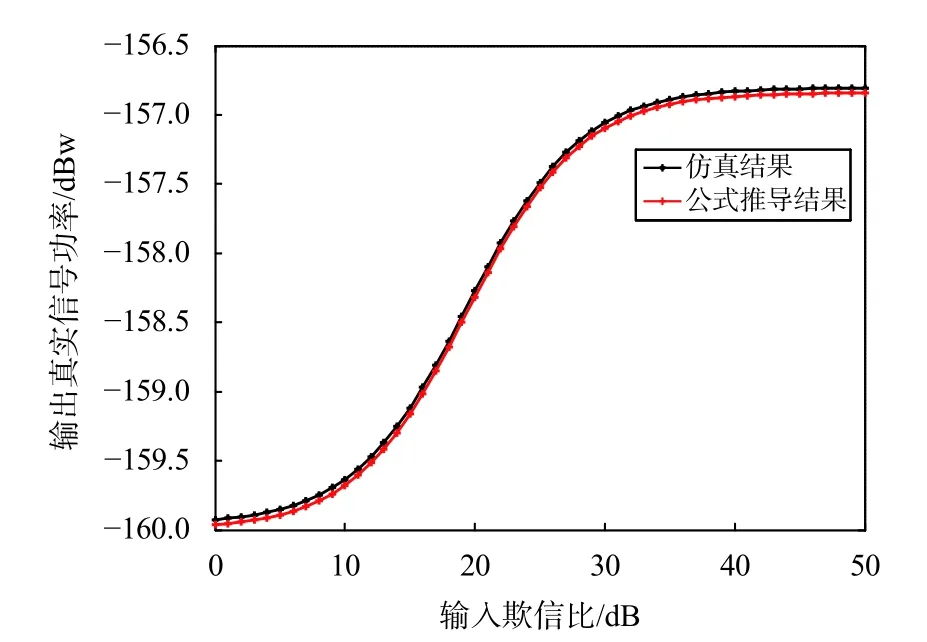
图2 输出真实信号功率随欺信比变化（场景1）

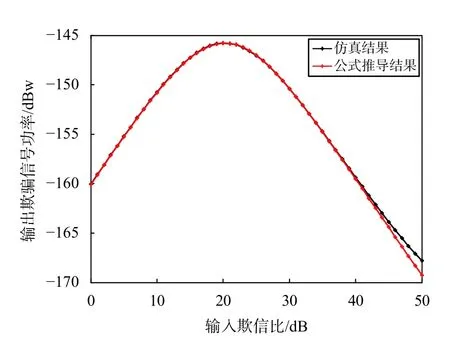
图3 输出欺骗信号功率随欺信比变化（场景1）

为了分析使用PI算法具体对导航接收机反欺骗性能的影响，如图4所示，本文给出了接收机输出导航信号和欺骗信号的载噪比随着输入欺信比的变化.

图4 输出信号载噪比随欺信比变化（场景1）

为了直观地体现出PI算法对欺骗信号的抑制效果，本文引入了欺骗抑制比这一指标，其定义为未使用抗欺骗算法输出的欺骗信号功率与经过抗欺骗算法处理后欺骗信号功率的比值，图5展示了欺骗抑制比随输入欺信比的变化图.

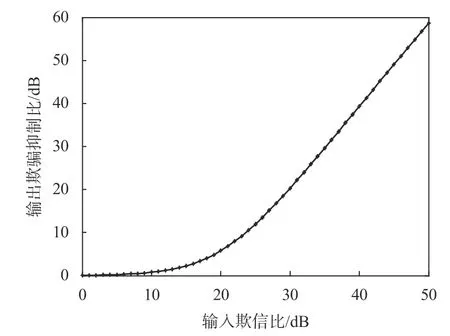
图5 欺骗抑制比随欺信比变化（场景1）

3.2 场景2

仿真场景2中信号设置如下：期望信号到达角(俯仰角，方位角)为[68°，135°]，功率为-160 dBw；欺骗信号到达角为[23°，95°]，功率与场景1相同，噪声和带宽设置不变. 欺骗信号比期望信号延迟30个码片.

在该信号设置下，计算得到相关系数为ρ=-0.007+0.011i，真实信号和欺骗信号的导向矢量 α1、α2以及二者的空间相关系数 α 如下：

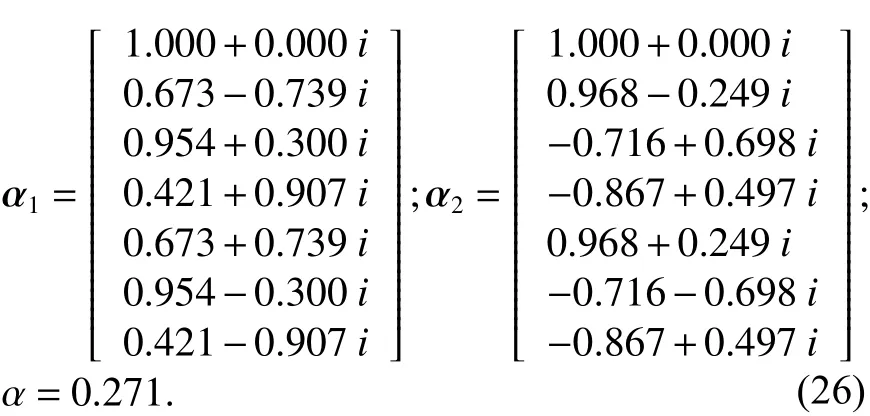
同样的，图6～9展示了在该场景下真实信号和欺骗信号输出功率、载噪比以及欺骗抑制比随着欺信比的变化.

图6 输出真实信号功率随欺信比变化（场景2）

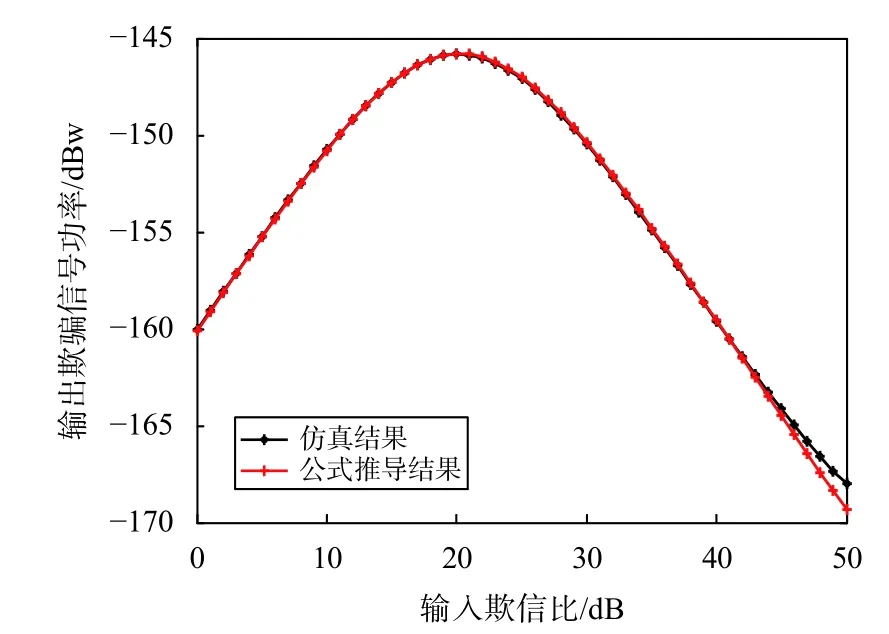
图7 输出欺骗信号功率随欺信比变化（场景2）

图9 欺骗抑制比随欺信比变化（场景2）

上面分别仿真了欺骗信号小延迟和大延迟的两个场景，可以看出仿真结果和理论分析的曲线均十分接近，对于真实信号而言，输出功率随欺信比的增长而变化，其增长和衰减与导向矢量的相关系数 α 有关.当 α ＜0 时，输出功率随欺信比增加而小幅度增长，最后趋于稳定；当 α ＞0 时，输出功率随欺信比增加而降低，降低幅度不到2 dB.

对于欺骗信号，在两个场景中开始随着输入欺信比的增加，输出欺骗信号功率呈线性增长趋势，欺骗抑制比始终保持为0，PI算法此时并没有对欺骗进行抑制.当欺信比到达10 dB之后，增长放缓，在20 dB时到达最大值，随后开始下降，其欺骗抑制比也是从欺信比10 dB之后开始增加，说明欺骗信号在噪声水平之下时，PI算法是可以对欺骗进行抑制的理论和仿真结果均吻合，证明了上节的理论分析和化简结果正确.

下面对真实和欺骗信号的载噪比以及欺骗抑制比进行分析. 由图4～5以及图8～9可知，在中低欺信比区间即欺信比在10～20 dB，此时欺骗信号依旧在噪声水平之10～20 dB，PI算法已经识别出欺骗，并在欺骗信号来向形成了零陷.虽然未能将其抑制到真实信号水平之下，但是通过处理使得欺骗信号载噪比高于真实信号不到15 dB，对之后信号和信息层面的处理奠定基础.

图10 给出在场景1欺信比50 dB时的PI准则下的波束方向图.

此时天线阵在干扰来向形成了64.24 dB的零陷，零陷深度高于欺信比，使得欺骗信号功率比真实信号低10 dB左右，与图4中的结果相吻合.

4 实测验证

为了使结论更具有说服性，作者在暗室中搭建了一个天线阵平台，对采集数据进行实测分.通过标准监测接收机进行调零天线阵抗欺骗处理后的信号接收，记录欺信比增加时，输出欺骗信号的载噪比，图11为暗室环境.

图11 中右上角红框中为真实信号发射天线，左下角红框中为欺骗信号发射天线，使用导航信号源发射导航信号和欺骗信号，阵列天线放置在暗室中心，其阵元排布为上文中描述的7阵元中心圆阵，硬件处理带宽为14 MHz. 通过可调功率衰减器将欺骗信号功率从-160～-110 dBw遍历，记录PI算法处理后的真实信号和欺骗信号的载噪比，得到原始数据，为了直观描述，将得到的数据结果如图12～13所示，分别得到信号载噪比随欺信比的变化图以及欺骗抑制比曲线图.

图11 暗室环境

图12 信号载噪比变化

图13 欺骗抑制比变化

由图12～13的实际测试结果可知，整体变化趋势和理论分析相同. 在实际测试中当欺骗信号强度超过卫星信号功率(-160 dBw)10 dB以上时，PI算法便已完成了欺骗信号存在的识别，并开始了抗欺骗处理，随着欺骗干扰信号功率逐渐增加，抗欺骗处理后欺骗干扰信号载噪比不超过51 dB/Hz，高于真实信号载噪比不超过10 dB.

这验证了在导航欺骗环境中，欺骗信号功率在噪声水平之下时PI算法依然可以实现抗欺骗的功能，并且可以理论计算出算法处理后欺骗信号的功率.

5 结束语

本文对GNSS中PI算法的抗欺骗性能进行分析，推导出经过调零天线处理后的真实信号和欺骗信号的功率随输入欺骗信号功率的表达式，针对输出信号功率、载噪比和欺骗抑制比等指标来定量衡量PI算法的性能. 通过推导分析发现，即使到达天线阵口面的欺骗信号功率在噪声水平之下，PI算法依旧可以对其进行抑制，使得并且运用仿真和实测的数据验证了结论的正确性.

本文作者在理论上阐明了PI算法在导航系统中仍然具有抗欺骗能力，为天线阵抗欺骗提供了理论支撑，对后端的信号和信息层面的处理具有指导意义，对于导航对抗中欺骗与反欺骗的实施具有重要指导意义.

致谢：感谢国防科大导航中心团体对本研究的支持，感谢专业组内对问题的分析讨论.