基于复合伪码的多卫星信号联合捕获算法

张天骐， 孟莹， 王晓烨， 陈显露

(重庆邮电大学 通信与信息工程学院 信号与信息处理重庆市重点实验室，重庆 400065)

近年来，随着科技水平的不断进步以及人们生活水平的提高，全球导航卫星系统(global navigation satellite system,GNSS)[1-2]得到了快速的发展，但是随之而来的还有人们生活节奏的加快，对定位所需的时间也有了更进一步的要求，希望定位时间可以尽可能的缩短，然而接收机有时又难免处于所需捕获时间较长的冷启动情况下. 因此，如何在冷启动情况下减小定位所需的捕获时间也是一个值得研究的问题.

BOC及其衍生信号因为具有更加优良的频谱利用率以及抗干扰能力而在导航系统中得到了应用，但是BOC信号的捕获方法基本上都是对单星信号的捕获，对具有更短捕获时间的多星信号的联合捕获算法的研究却很少. 文献[3-6]分别采用经典的并行方法、伪相关函数法(pseudo-correlation function，PCF)、自相关边峰消除技术(autocorrelation side-peak cancellation technique，ASPeCT)以及平均相关和差分相干累积相结合的方法实现对单星BOC信号的捕获，但是总体而言，当需要捕获相同颗数的多颗卫星信号的时候，一次对多颗卫星信号进行同时捕获和多次进行单颗卫星信号的捕获时间之和相比更加节省时间. 其中仝海波等[7]通过对接收机位置、速度等关键参数的解算来实现对多卫星信号的联合捕获，但是该方法只适用于有辅助信息的热启动方式，而不适合没有辅助信息的冷启动方式. JAN等[8]通过伪码的复制和的方法实现对多卫星信号的联合捕获，但是该方法是建立在多普勒频偏已经被补偿的情况下，并不适合存在多普勒频偏且多普勒频偏未知的情况. DIESPOSTI等[9]提出将多路卫星信号相干地积累以提高处理增益，但该算法要求对载波相位进行搜索和同步，目前在捕获阶段难以实现，而且上述文献[7-9]也仅仅是对直扩信号进行了讨论，而没有对BOC信号进行讨论.

针对上述BOC信号的多卫星信号联合捕获算法缺乏的问题，该文提出了一种基于复合伪码的多卫星信号联合捕获算法. 该算法首先将不同卫星信号所对应的伪码进行组合来实现接收机对不同的卫星信号同时捕获的能力，然后通过频域的循环移位来实现对多普勒频偏的补偿，最后将经过多普勒频偏补偿的接收信号与复合伪码的相关结果经过TK算子来实现对噪声的抑制，提升信号的处理增益，进而能够提高信号的检测概率.

1 BOC信号模型

BOC信号作为一种具有更加优良的频谱共享，抗干扰以及抗噪能力的信号，在导航卫星系统中得到了十分广泛的应用，其具体产生框图可表示如图1所示.

图1 BOC信号产生框图

在高斯白噪声信道下的BOC接收信号可以表示如下：

(1)

式中：M为可见卫星的总数；m为第m颗可见卫星；n(t)为高斯白噪声；rm(t)表示第m颗卫星的接收信号，其中rm(t)可以进一步表示如下：

rm(t)=dm(t)Sm(t-τm)xm(t)=

dm(t)sBOC(t-τm)c(t-τm)xm(t)

(2)

其中xm(t)=exp[j2π(f0+fdm)t+φm]代表载波信号；f0代表载波频率；fdm代表第m颗可见卫星的多普勒频偏；φm代表第m颗可见卫星的初始相位；sBOC(t-τm)和c(t-τm)代表延时为τm的副载波信号以及伪码信号.

将接收信号经过下变频和模数转换后得到的离散信号可表示如下：

exp[j(2πfdmn/fs+φm)]+N(n)

(3)

2 捕获算法原理

2.1 复合伪码算法

复合伪码算法的基本原理是首先生成多个不同卫星信号的组合伪码，然后将不同的组合伪码迭加起来生成一种新的复合伪码，其具体表达方式可表示如下：

(4)

其中c(i)(n)代表卫星i所对应的组合伪码；c(n)代表由不同卫星信号的组合伪码相组合所生成的复合伪码. 得到复合伪码后将复合伪码与接收信号进行相关. 单星捕获方法是在信号捕获的时刻仅仅利用单个卫星信号的组合伪码，本文所应用的复合伪码将不同的组合伪码相加可以实现同时对多个卫星信号进行搜索与检测. 此时，若当前接收信号中不存在可见卫星，相关结果中将不存在相关峰值，则可以一次否定K颗卫星；若接收信号中存在一颗或多颗可见卫星时，相关结果中将会出现一个或多个峰值，此时则可以一次捕获到一颗或多颗卫星. 此外，当同时对K颗卫星信号进行捕获的时候，就相当于将采用单星捕获方法进行K次捕获所需要的K颗卫星信号的总捕获时间大约减小到了原来的1/K. 因此，相对于多次进行单颗卫星信号的捕获所利用的总捕获时间而言，此方法在捕获相同数量的卫星信号时可以在减小计算量的同时很大程度上减小捕获时间.

2.2 多普勒频偏补偿算法

将接收信号y(n)按次序选取L点进行FFT运算得到频域信号Y(k)，假设Y[(k)]L代表以L为周期对Y(k)进行周期延拓，RL(k)代表长度为L的矩形窗，则

Y(k)=Y[(k)]LRL(k)

(5)

因为频域信号的循环移位等于时域信号相乘，所以将频域信号Y(k)进行循环移位就可以实现对不同多普勒频偏的补偿[10]. 具体表达式可表示如下：

F-1{Y[(k+lm)]LRL(k)}=

(6)

其中F-1{·}代表逆FFT运算；Y[(k+lm)]LRL(k)代表将Y(k)循环左移lm位，通过上式可以看出Y(k)在频域循环左移lm位等同于将y(n)在时域乘以一个频率为lm/L复正弦信号，当lm满足fdm=lmfs/L时上式的值最小，也即多普勒频偏对信号的幅值衰减的影响达到最小.

通过对式(6)的分析可以发现通过在频域上对信号进行循环移位就可以在时域上实现对多普勒频偏的补偿. 因此，采用此方法仅仅通过一次FFT运算以及若干次的循环移位就可以实现对多普勒频偏的并行式补偿，最后通过将经过多普勒频偏补偿后的接收信号与复合伪码的乘积进行一次IFFT变换就可以得到接收信号与复合伪码的相关结果. 因此，此方法在很大程度上提高了对信号的处理速度.

2.3 TK算子

非线性二次TK算子作为一种能够对能量进行测定的方法，不仅具有结构简单的优点，而且具有能够很好的跟踪信号的瞬时变化的优点[11-12]，且通过文献[13-14]可以得到，TK算子的基本表达式可以表示如下：

(7)

式中：z′(t)代表函数z(t)的一阶导数；z″(t)代表函数z(t)的二阶导数；*代表取信号的复共轭. 根据式(7)可以将TK算子的离散形式表示如下：

ψd[z(n)]=z(n-1)[z(n-1)]*-

z(n)[z(n-2)]*}

(8)

将相关结果带入式(8)可得

(9)

式中：Rz(τ)代表经过多普勒频偏补偿后的接收信号与复合伪码的相关结果；sgn(t)代表符号函数；δ(t)代表冲激函数；Δn(τ)代表所有与噪声相关的作用项；rect(t,Tc)代表矩形函数，其表达式可表示如下：

(10)

根据式(9)可以看出，TK算子只有在τm时刻才会有很大的输出，在其他时刻的输出都会很小. 因此，TK算法可以在一定程度上对噪声信号存在抑制作用，进而提高信号的处理增益，提高信号的检测概率.

3 整体捕获算法

为了在不过多增加计算量的同时缩短冷启动时信号的捕获时间，本文提出了一种基于复合伪码的捕获算法. 该方法可以通过组合不同的组合伪码数量来实现对不同卫星信号的同时捕获，该文的捕获算法框图主要以3个组合伪码相组合生成的复合伪码为例来进行阐述，其具体捕获算法框图可表示如图2所示.

图2 捕获算法框图

捕获算法具体步骤可表示如下.

步骤1：将接收信号进行下变频和模数转换处理后以伪码速率进行采样，得到离散信号.

步骤2：将采样后的信号经过本地载波数字控制振荡器进行载波剥离.

步骤3：将不同卫星所对应的伪码进行组合生成复合伪码.

步骤4：将经过载波剥离后的接收信号和复合伪码分别进行FFT运算，然后对复合伪码的运算结果取复共轭运算.

步骤5：根据频偏的范围对接收信号的FFT运算结果分别向左和向右进行k次移位操作，得到2k+1个频偏补偿序列.

步骤6：将2k+1个频偏补偿序列和复合伪码的FFT运算结果的复共轭相乘后进行IFFT运算，得到2k+1个相关序列.

步骤7：检测相关序列中的前3大值然后对其进行平均运算，从而得到3个卫星信号的最佳频偏补偿序列.

步骤8：将步骤7中所得到的相关序列进行TK运算，并将相关峰的最大值，次大值以及第3大值分别与第四大值的比值作为门限判决的变量.

步骤9：将门限判决变量和预设的门限值比较，如果存在门限判决变量大于预设的门限值，则认为捕获成功，如果门限判决变量小于预设的门限值，则滑动复合伪码，重复步骤4～步骤8，继续进行门限值的比较.

4 仿真分析

为了检测所提出的算法的捕获性能，本文对BOC(1,1)信号进行了仿真，其中信号的采样频率设置为16.368 MHz，码速率设置为1.023 MHz，信号采样长度设置为8 184，多普勒频偏分别设置为1 700 Hz，3 900 Hz以及6 000 Hz，码偏移量分别设置为350，450以及550个码片.

① 仿真1 频偏补偿序列的选取.

该仿真为了验证该算法对多普勒频偏的补偿效果，将接收信号分别进行了10次循环左移和10次循环右移操作，然后加上未进行循环移位的序列一共得到了21个相关序列，其仿真结果如图3所示.

通过图3可以看出，当多普勒频偏补偿序号为-3,-2和-1时能够得到明显比其他多普勒频偏补偿序号高的多的峰值. 此外，通过图3可以看出，当多普勒频偏补偿序号为-3时所对应的峰值最高，多普勒频偏补偿序号为-1时所对应的峰值最低，出现此现象的原因是当多普勒频偏为6 000 Hz时是完美补偿，而当多普勒频偏为3 900 Hz和1 700 Hz时不是完美补偿，而完美补偿时的峰值衰减比非完美补偿时的峰值衰减小，因此完美补偿时峰值比非完美补偿时峰值高.

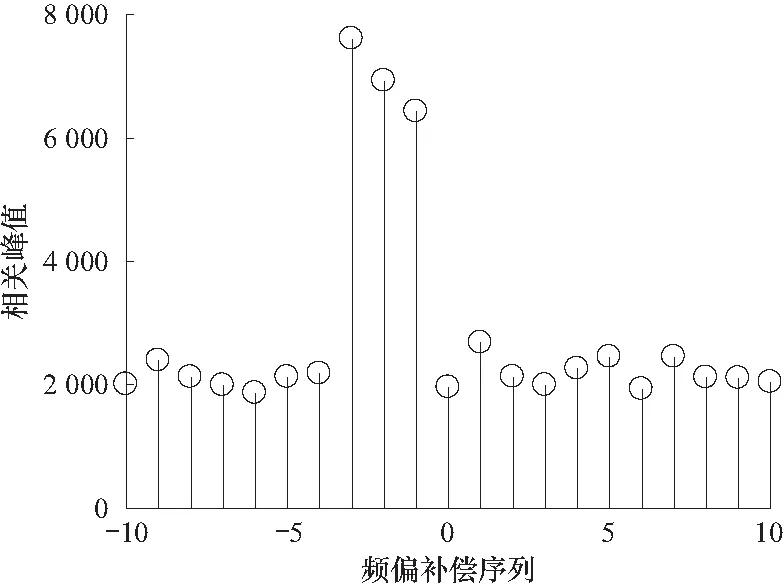
图3 多普勒频偏补偿序列

② 仿真2 峰值对比仿真.

该仿真为了验证TK算子对噪声的抑制作用，分别对信号的相关结果以及经过TK算子之后的运算结果进行了仿真，其仿真结果如图4所示.

图4 相关峰对比

通过图4可以看出，相关法和TK算子法均在相同位置出现了峰值，但是经过TK算子后的噪声比相关法的噪声小很多，这正是因为TK算子对噪声具有很好的抑制作用. 因此，此实验不仅证明了TK算子对噪声具有很好的抑制作用，也从侧面说明了TK算子的应用可以很好的提高信号的处理增益.

③ 仿真3 虚警概率仿真.

因为在实际情况下接收信号的噪声功率可能很难测定，所以如果仅仅利用单纯的绝对能量进行判决可能会存在一定的弊端. 因此，该文选取通过比例峰值的方法来进行判决. 该仿真在假设接收信号中不存在检测信号的情况下，通过比例峰值的判决方法对相关法和TK算法的虚警概率进行了仿真，其仿真结果如图5所示.

图5 虚警概率

通过图5可以看出，随着门限值的提高，检测概率逐渐减小，且当相关法的门限值为1.2，TK算法的门限值为1.5的时候，相关法和TK算法的虚警概率相同. 当门限值达到2.1的时候，相关法和TK算法的虚警概率都降为0.

④ 仿真4 不同算法检测概率.

为了验证该文所提算法的检测性能，该仿真将相关法和TK算法的门限值分别设置为1.2和1.5，进行了同虚警情况下的仿真对比，以及在阈值设置同为2.1时对相关法和TK算法进行了同检测门限下的仿真对比. 其仿真结果如图6所示.

通过图6可以看出，在同虚警的情况下，TK法的信号1和相关法的信号1的检测概率相同，TK法的信号2的检测概率比相关法的信号2的检测概率高大约2 dB，TK法的信号3的检测概率比相关法的信号3的检测概率高大约5 dB. 在阈值同为2.1的情况下，TK法的信号1，信号2，信号3的检测概率分别在-12 dB，-8 dB， -6 dB的情况下达到1，而相关法的检测概率在0 dB之前都为0. 通过仿真结果可以发现，TK算法和相关法相比对噪声有抑制作用，提高了信号的处理增益，所以TK算法的检测概率高于相关法的检测概率.

图6 检测概率

⑤ 仿真5 不同信号个数检测概率.

不同复合伪码的数量会对噪声产生影响，因此本仿真分别对两信号和三信号以及四信号的检测概率进行了仿真，其中两信号中信号1和信号2的多普勒频偏以及码偏移量的设置和三信号中的信号1和信号3的多普勒频偏和码偏移量设置相同，四信号相比三信号增加了多普勒频偏为3 800 Hz，码偏移量为400 码片的信号，其仿真结果如图7所示.

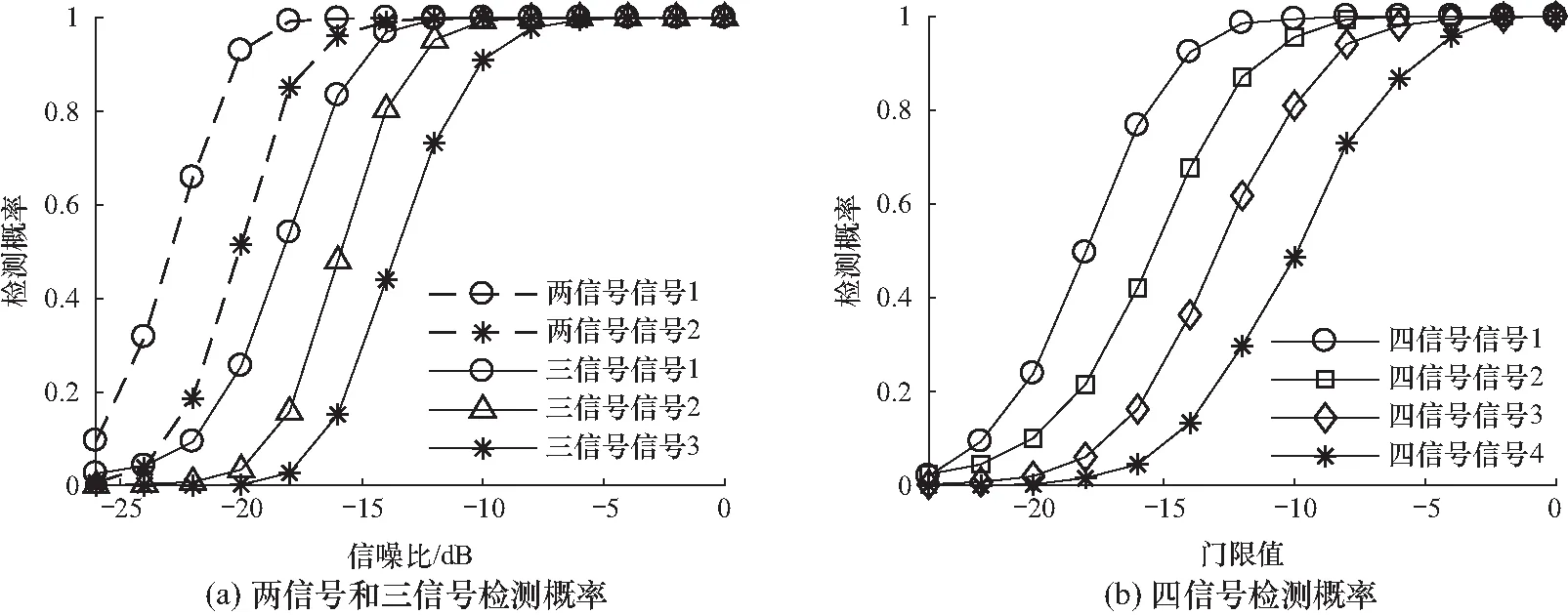
图7 不同信号检测概率

通过图7可以看出，两信号的检测概率高于三信号的检测概率，三信号的检测概率高于四信号的检测概率，其中两信号的检测概率比三信号的检测概率分别高3 dB和4 dB,三信号的检测概率普遍比四信号的检测概率高大约2 dB，两信号联合检测的概率比3信号联合检测的概率高，三信号的检测概率比四信号的检测概率高的原因是随着复合伪码的数量增加，噪声也会随之增加，检测概率就会相应的减小，因此两信号的检测概率高于三信号的检测概率.

⑥ 仿真6 不同信号检测概率.

为了验证该文算法的适用性比较广泛，本仿真分别对BOC的衍生信号DBOC信号以及CBOC信号也进行了同虚警情况下的检测概率的仿真，仿真结果如图8所示.

通过图8可以看出，同虚警情况下CBOC信号的3个信号可在-14 dB，-12 dB，-10 dB实现对信号捕获，DBOC信号的3个信号可以在-16 dB，-14 dB，-10 dB实现对信号的捕获. 通过仿真结果可知，该文所提算法不仅能实现对BOC信号的捕获，还能实现对DBOC信号以及CBOC信号的捕获，具有广泛适用性.

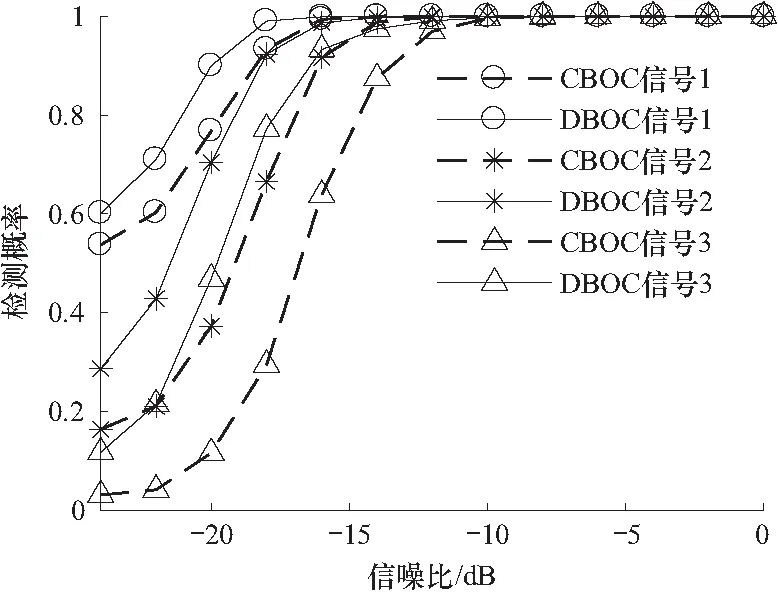
图8 不同信号检测概率

⑦ 仿真7 累加检测概率.

TK算子法的另一个优点是可以通过多次进行TK运算来进一步提升对噪声的抑制作用，该实验分别在一次和两次TK运算次数下对信号1，信号2以及信号3的检测概率进行了仿真，其仿真结果如图9所示.

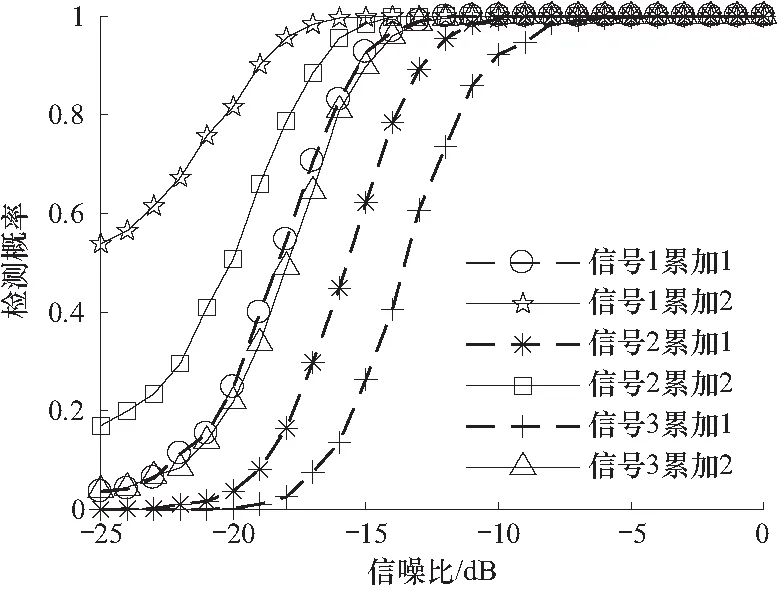
图9 累加检测概率

通过图9可以看出，信号1累加两次的检测概率比累加一次的检测概率高出大约4 dB，可以在-16 dB的时候实现对信号的捕获. 信号2累加两次比累加一次的检测概率高大约5 dB，可以在-14 dB的时候实现对信号的捕获. 信号3累加两次比累加一次的检测概率高大约6 dB，可以在-12 dB的时候实现对信号的捕获.

⑧ 仿真8 平均捕获时间.

平均捕获时间也是衡量捕获性能的一个重要因素，因此本仿真对相关法以及TK算子法在不同信噪比下的平均捕获时间进行了仿真，其仿真结果如图10所示.

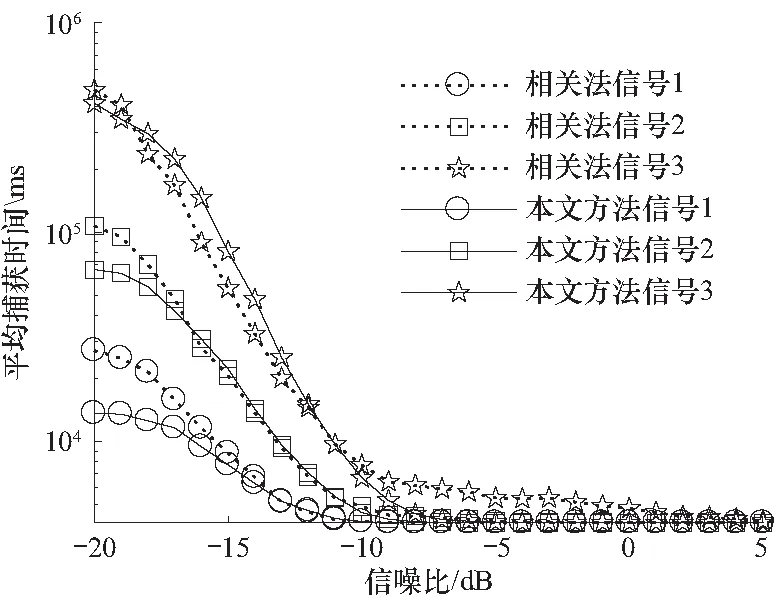
图10 平均捕获时间

通过图10可以发现，在不同的信噪比下，本文所提的TK算法对信号1、信号2和信号3的平均捕获时间均低于相关法的平均捕获时间，其中本文所提算法对信号1的捕获大约可以在-10 dB时达到最低，对信号2的捕获大约可以在-8 dB时达到最低，对信号3的捕获大约可以在-6 dB时达到最低.

5 结 论

本文所提算法可以实现同时对多颗卫星信号的捕获，可以在一定程度上降低冷启动时的捕获时间，且通过TK算子处理可以降低噪声的影响，提高对信号的检测概率. 通过仿真可得，在同虚警的情况下，本文算法最高可以比相关算法的捕获性能提高5 dB，在完美补偿且经过两次TK运算时，可以在-16 dB的情况下实现对信号的捕获.