基于四值逻辑的伽罗华域AB+C电路设计

吴海霞， 李凌宇， 王天， 王兴华， 李潇然

(北京理工大学 信息与电子学院，北京 100081)

相对于布尔逻辑计算模式而言，多值逻辑计算模式在理论上具有更为强大的计算能力. 多值电流模(multiple-valued current-mode，MVCM)电路在降低硬件复杂性方面具有更大的潜能，因为在该类电路中，不仅一根线可以承载多于1位的数据，而且算术运算中频繁使用的线性和运算可以简单地通过线的直接连接而实现，不需要任何器件[1-5]. 伽罗华域运算在通信领域包括纠错编码、加密运算及数字信号处理等方面起着重要的作用. 越来越多的应用都需要VLSI实现以满足面积、速度及安全性的要求，而且这些应用的有效性很大程度上取决于伽罗华域算术运算的有效性. 目前伽罗华域运算的实现主要是基于布尔逻辑，存在的主要问题是延迟太长和硬件太大. 因此，迫切需要针对这些运算操作的有效算法和简化的硬件结构[6-10]. 针对上述问题，本文主要讨论了GF(24) 上基于四值逻辑的AB+C算法及其基于多值电流模的并进并出脉动电路的实现.

1 建立四值逻辑与伽罗华域的关系

GF(2k)域元素有很多种表示形式和方法. 若k为两个整数的积,k=nm， 那么通过GF(2n)来描述GF(2k),可以得到该域的不同表示方法. 这样，域GF(2n)，通过它来描述合成域， 被称为基域. 因此，对于四进制的有限域，基域为GF(22) =GF(4). 合成域是指在GF(2k)的某个子域GF(2n)上而不是素域GF(2)上定义的扩展域. 用GF((22)m)表示四进制合成域，GF(2k)表示通过素域GF(2)定义的二进制扩展域. 一个域GF(2k)，若其具有确定的k值、确定的不可约多项式及确定的初始元素，那么它就具有确定的2k个域元素，无论是用二进制扩展域GF(2k)或是合成域GF((22)m)表示，代表的是同一个域. 这些完全不同的表示方法之间可以相互转换[3].

利用初始元素β和最佳不可约多项式f(x)=x2+x+1构成域GF(22)，其对应的4种表示方法，β表示、多项式表示、2-位二进制表示及1-位四进制表示，如表1所示.

用1-位四进制0、1、2、3和2-位二进制表示GF(4)中的元素后，图1给出了其模乘和模加的定义，其中符号⊗和⊕分别表示这两种算术运算. 这些运算在运算过程中不涉及任何进位，可以简化硬件实现.

图1 GF(4)的模乘和模加运算

利用初始元素0100和初始不可约多项式f(x)=x4+x+1构造域GF(24)，其对应的合成域GF((22)2)的最佳不可约多项式可以推导得出为f(x)=x2+x+3. 进而得出其相应的5种表示法：α表示，GF(24)的多项式表示和4-位二进制表示，及GF((22)2)的4-位二进制表示和2-位四进制表示[3,9-10,12]. 表2给出了这5种不同的表示，并显示了合成域GF((22)2)如何与四进制及二进制域GF(24)建立联系. 通过这样的转换和表述，可以看出基2的合成域运算比较适合利用多值逻辑来实现，例如，GF((22)m)运算适于利用四值逻辑来实现. 多值逻辑表示的每一个数据位承载多于1-bit的信息，在二值逻辑系统每次处理1-bit信息，而在多值逻辑系统每次处理多于1-bit信息，因此有希望获得处理速度的改善及硬件连线的减少.

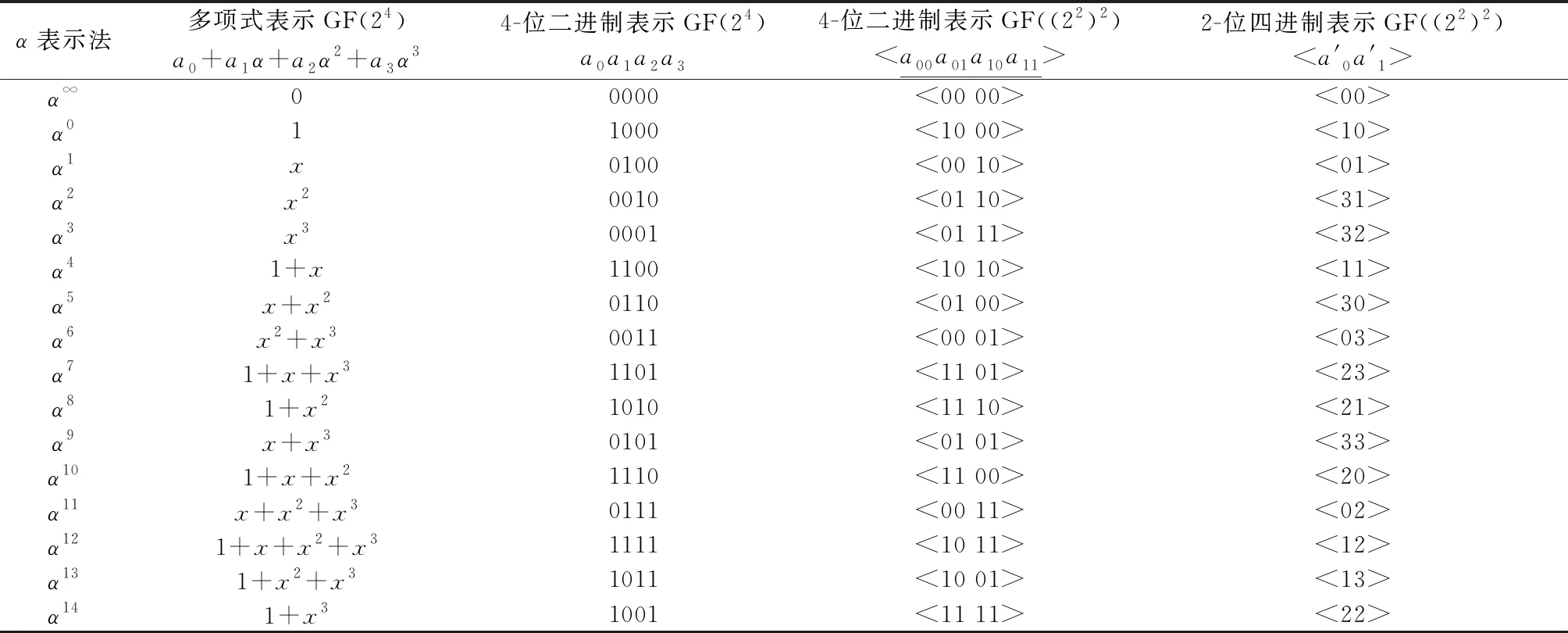
表2 同一域的不同表示法：GF(24)和GF((22)2)

2 MVCM电路的基本原理

MVCM电路的基本结构如图2所示，通常包括3个基本组件，线性和、阈值比较器和输出生成器. 本文采用基于动态源极耦合逻辑的MVCM电路架构，其上述3个基本元件的电路原理图如图3所示. 在阈值比较器中，首先将四值电流模输入信号I(X) 转换为电压信号V(X)，然后V(X)与阈值V(T)进行比较并产生二值差分输出信号(G,G′)；信号(G,G′)作为输出生成器的输入信号控制输出信号的生成；线性和是通过将信号线直接连接在一起来实现；这样，最终输出的是电流模信号[1-2]. 因此，可以看出输出生成器是设计的关键. 本文采用文献[12]中GF(4)的四进制模乘和模加器，分别用图4所示的两个符号表示这两个模块.

图2 MVCM电路的基本结构

图3 MVCM基本组件的电路原理图

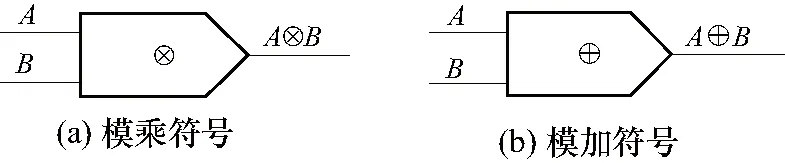
图4 模乘和模加符号

3 基于四值逻辑的脉动积-和AB+C运算算法

在GF((22)2)中，假设A=a0+a1α,B=b0+b1α及C=c0+c1α，对应的不可约多项式为f(x)=x2+f1x+f0，那么AB+C定义为

AB+C=(a0+a1α)(b0+b1α)×modf(x)+(c0+c1α)

(1)

因为初始元素α是f(x)的一个根，且根据GF域的基本特性α=-α，得到

f(x)=x2+f1x+f0⟹α2+f1α+f0=0⟹

α2=-f1α-f0⟹α2=f1α+f0

将α2=f1α+f0带入公式(1), 得到下列等式[3]

R=AB+C=R0+R1α

其中R1=b1(a1f1+a0)+a1b0+c1,

(2)

R0=b1a1f0+a0b0+c0

(3)

考察等式(2)和(3)，可以将其分解为公式(4)及公式(5)所示的运算层次. 分析R1和R0的表达式，可以看出它们都可以通过3个独立的积-和运算来实现，可以采用二级流水结构来提高数据运算的吞吐量，从而提高处理速度.

(4)

(5)

随机以A=B=C=α8为例，简单说明如何在GF(24)及GF((22)2)上进行AB+C运算. 首先，利用二值逻辑在GF(24)上计算AB+C，并依据表2，将其结果转换为四进制表示.

AB+C=α8·α8+α8=α16mod15+α8=

α+α8=0100+1010=1110=α10=〈20〉

(6)

接下来，利用四值逻辑在GF((22)2)上计算AB+C.

步骤1:GF((22)2)的不可约多项式是x2+x+3,所以f1=1,f0=3；并依据表2的转换，可以得到

A=B=C=α8=〈21〉

步骤2：根据等式(2)(3), 可得

(7)

等式 (6) 和 (7)表明采用上述两种逻辑系统进行运算，所得结果相同.

依据等式(4)和(5)，在GF((22)2)上进行AB+C运算需要两级积-和迭代. 据此，基于四值逻辑构建的并入并出脉动阵列电路结构如图5所示，模块 PE1和PE2见图6所示， D触发器和T 锁存器用以同步信号，具体结构参见文献[11].

图5 四进制AB+C 脉动结构

图6描述了AB+C脉动电路中的信号同步，a0a1,b0b1,c0c1和f0f1是原始输入信号.

图6 AB+C脉动电路中的信号同步

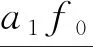
4 分析验证

在0.18 μm CMOS工艺下对本文的设计进行了仿真验证，图7显示了时钟周期为10 ns 的输入和输出波形，可以看出经过5个时钟周期后，在时钟下降沿输出运算结果，图中的竖线表示从该时刻开始输出运算结果. 图8给出了对应图7的输出时序分析，可以看到在第(n+5)个时钟周期下降沿输出第n个输入的运算结果，输出结果与理论计算值一致. 本设计中四值逻辑0、1、2、3对应的电压值为0.3 V、1 V、1.3 V及1.8 V. 表3给出了与文献中相应二值逻辑及四值逻辑实现技术的比较. 相对于文献[3]基于二值逻辑的实现技术，本设计的首次延时减小了54%，晶体管数目与连线数目总和减少了5%，尽管相对于该文献中基于神经元MOSFET的多值电压模实现技术，没有明显的改善.

图7 AB+C输入和输出波形

图8 AB+C的仿真数据的时序分析

表3 GF(24)上AB+C运算的性能对照

5 结 论

本文给出了一种基于四值逻辑的GF(24)上AB+C的算法及其基于MVCM并入并出脉动阵列结构的电路实现. 在0.18 μm CMOS工艺下进行了HSPICE电路仿真，并与已发表的文献进行了性能比较. 与相应的基于二值逻辑的CMOS实现相比，首次延迟明显减少，晶体管和连线的数目和也有一定程度的减少. 本文所提的脉动阵列电路，结构简单、规整、模块化，适于作为算术运算处理器芯片的基本模块，应用于加密、纠错编码、数字信号处理等领域. 本项工作显示，MVCM电路与相应的基于MVL算法的结合是实现GF(2k)超高性能运算单元的一个潜在的解决方案. 在应用层面有限域运算通常是大数据位的运算，例如ECC加密的数据长度一般大于150 bit. 多值逻辑的运算优势在大数据位的运算系统中会有更为明显的体现，因此研究基于多值逻辑的大数据位的GF (2k)的运算算法及其VLSI实现，将是未来研究工作的一个方向. 另外，噪声一直是多值逻辑实现技术关注的问题，在保持高转换速度的同时降低噪声和静态功耗将是未来研究工作的重点. 如果这些问题能够很好解决，多值逻辑技术将成为获得高性能运算芯片的一个切实可行途径.