基于滑套位置角的无同步器变速器换挡过程非线性动力学特性研究
2022-01-23宋强章伟
宋强, 章伟
(1.北京理工大学 机械与车辆学院,北京 100081;2.电动车辆国家工程实验室,北京 100081)
电驱动机械变速器具有效率高、成本低、结构简单等优势,近年来已成为产业界和学术界的关注热点. 同时由于电机技术以及电机控制技术在新能源汽车上的应用及发展,使得无同步器的AMT变速器慢慢得到应用. 无同步器的AMT的换挡过程由电机主动同步,由换挡执行机构控制滑套和接合齿圈的结合,从而完成换挡. 滑套与齿圈作为无同步器AMT中为数不多的动力耦合零件,一方面与传动系负载相连,受到来自路面的激励作用,另一方面其转速是电机调速阶段的调速目标,起到承上启下的作用,因此它们的接合对换挡过程的时间和平顺性具有较大影响. BKA等[1]建立了无同步器变速器系统的动力学模型及换挡啮合成功概率数学模型,分析了影响换挡品质的主要因素是滑套和结合齿圈相对转角和相对转速. 当无同步器换挡滑套和接合齿圈的转速差过小会造成同步顶齿现象和增加同步时间,转速差过大则会造成非同步打齿现象[2-4]. 陈红旭[5]通过建立混杂自动机模型,仿真分析了电机-变速器直连系统,发现直连系统的换挡品质可以优于有离合器系统. 在分析滑套和结合齿圈接触冲击过程时,LU等[6]则使用非线性的弹簧阻尼模型对换挡过程中的冲击进行分析,并提出了求解阻尼比的方法. 隋立起等[7]建立了考虑齿轮耦合振动的换挡过程非线性动力学模型. 孙丹婷等[8]以有同步器两挡AMT为研究对象,建立了换挡过程线性和非线性动力学模型,分析了线性和非线性条件下换挡过程各阶段接合套转速波动和动力学行为.
在AMT换挡系统中,无论是有同步器还是无同步器,齿轮系统都处于高速旋转的啮合状态中. 细微的参数变化会引起整个系统的振动,对变速器系统的性能、使用寿命、换挡品质造成影响. 从齿轮动力学的方面研究齿轮振动对换挡系统的影响,但是往往忽略了滑套及齿圈的接合过程的动力学特性对换挡过程的影响[9-11]. 因此,有必要对滑套和接合齿圈的啮合过程的动力学特性进行深入研究. 针对滑套和接合齿圈,将滑套和齿圈的啮合过程划分为多种情况,通过定义滑套位置角,判定区分具体的接合碰撞情况. 运用非线性接触冲击模型,建立滑套和接合齿圈的非线性动力学模型. 考虑啮合刚度、啮合阻尼、齿侧间隙等非线性因素,建立换挡过程的非线性动力学模型,之后分析不同的轴向换挡力对AMT换挡过程的影响,为无同步器AMT的换挡品质的提高和工程应用提供参考.
1 无同步器AMT换挡过程分析
1.1 换挡过程阶段划分
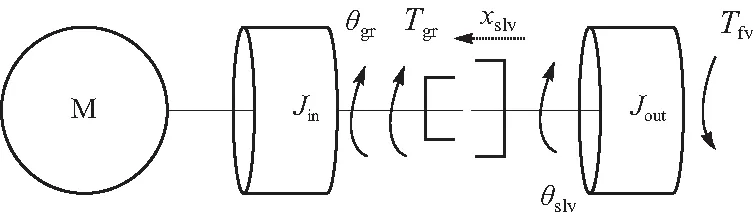
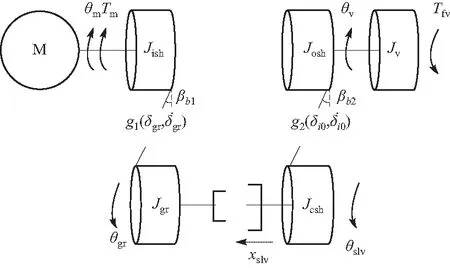
以两挡AMT换挡系统为例,如图1所示. 无同步器AMT系统的动力耦合零件只有滑套与接合齿圈,换挡阶段可以划分为电机转矩卸载、摘挡、电机同步调速、挂挡以及转矩恢复5个阶段. 其中,挂挡阶段又可细分为滑套自由行程阶段、滑套与齿圈碰撞阶段、滑套与齿圈结合阶段. 具体的换挡过程中各物理阶段的示意图如图2所示.
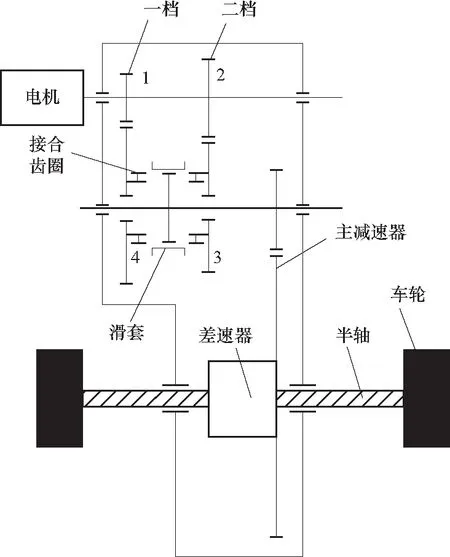
图1 两档AMT换挡系统示意图
图2中Tin为齿圈所受驱动转矩;Tfs为滑套受到来自车轮端的阻力转矩;ωin、ωslv分别为齿圈和滑套的角速度;xslv为滑套轴向位移;FS为轴向换挡力;滑套所受的滑动阻力由两部分组成,Fg为滑套与齿圈之间由重力引起的滑动摩擦力,FB为滑套与花键毂之间由于弹簧定位销压紧力引起的滑动摩擦力;Tgr、ωgr为接合齿圈所受的扭矩和角度.

图2 无同步器AMT换挡过程各物理阶段示意图
1.2 挂挡阶段及碰撞情况划分
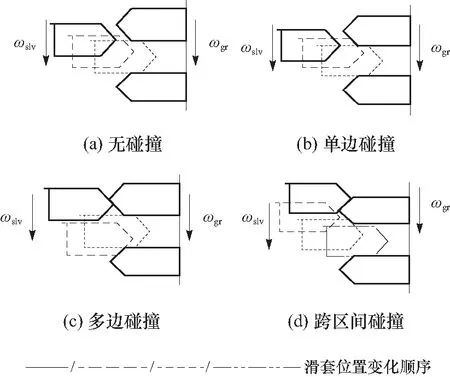
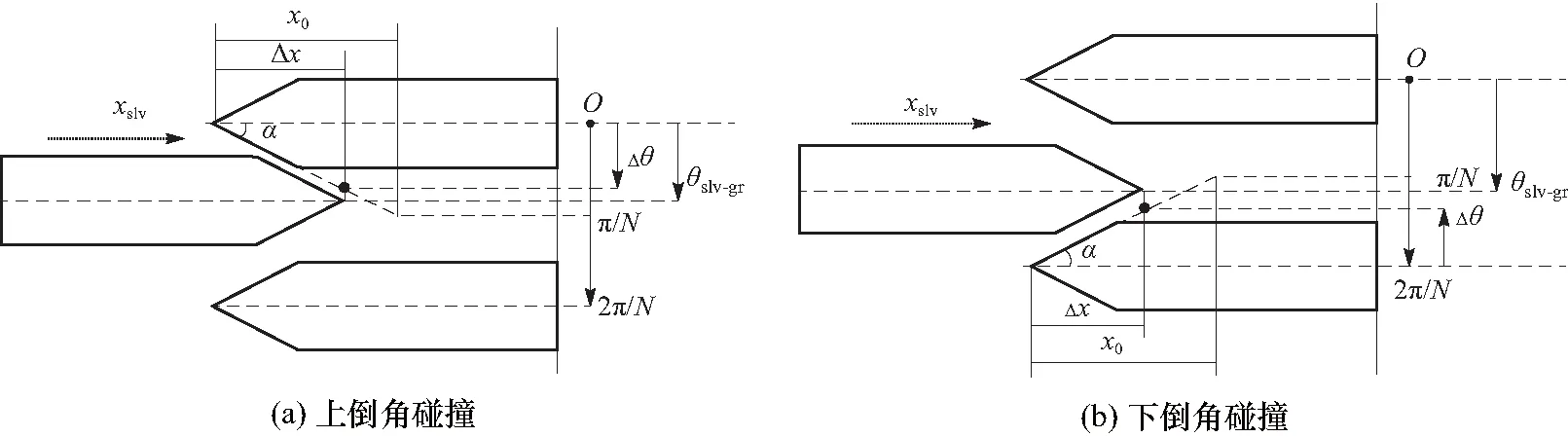
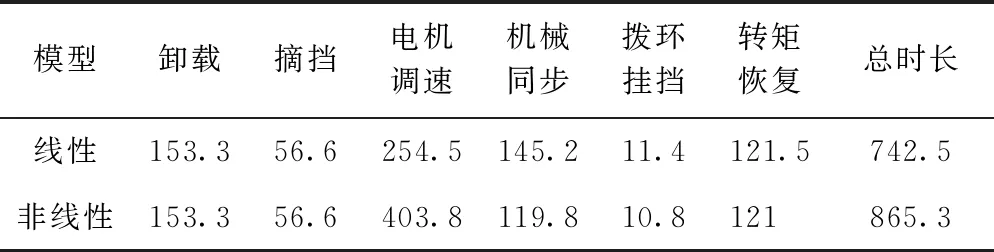
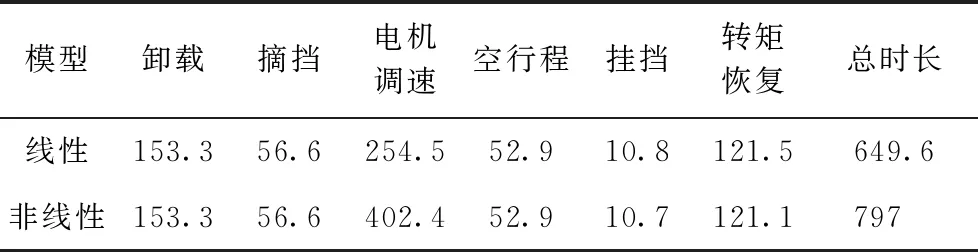
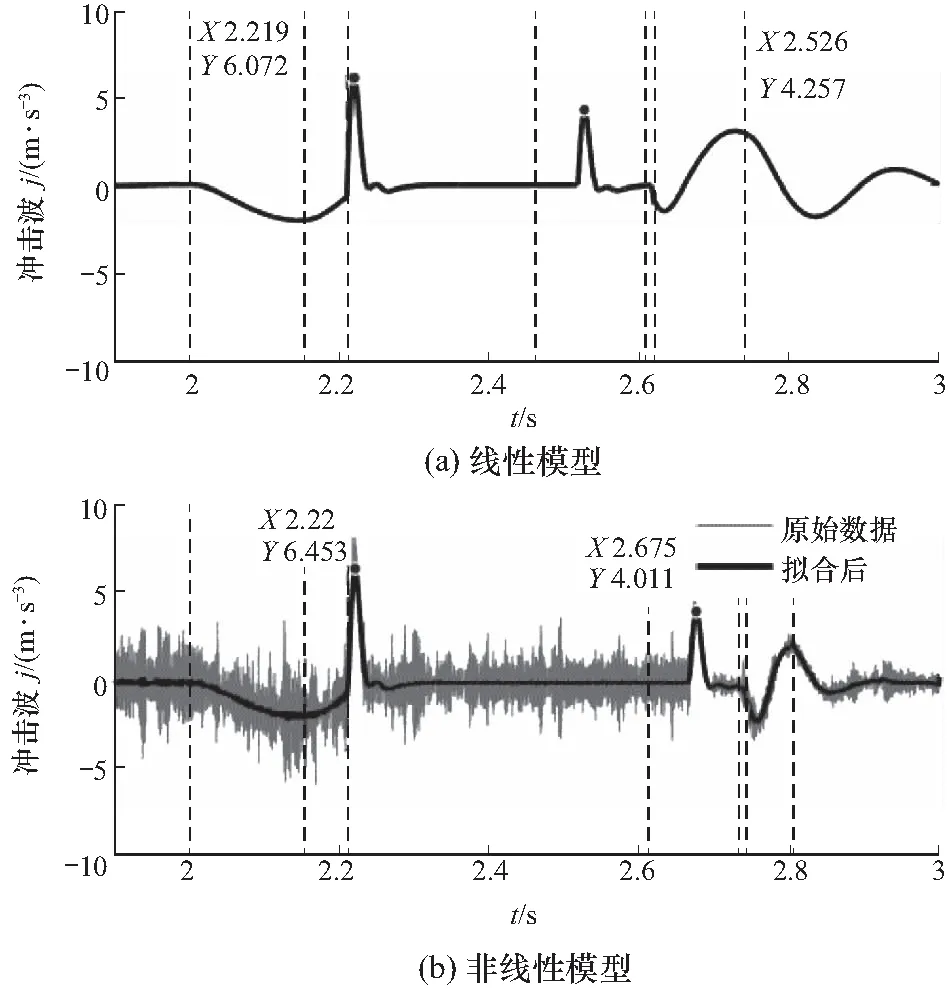
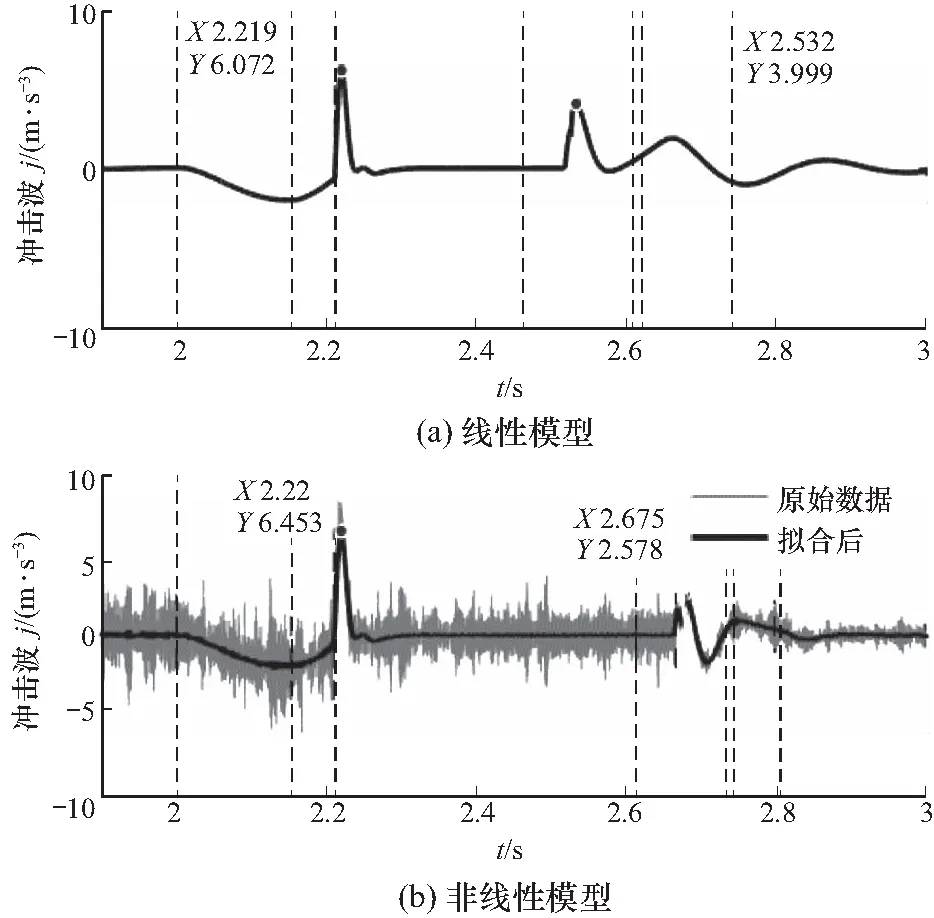
根据挂挡阶段的划分,滑套从空挡中心位置开始轴向运动,如图3所示. 滑套齿尖与齿圈齿尖之间距离为s1,当0 图3 挂挡子阶段滑套位置节点示意图 而挂挡阶段中的碰撞情况又可细分为4种,分别是无碰撞、单边碰撞、多边碰撞、跨区间碰撞,如图4所示. 图中无碰撞,即齿接合之前,滑套与齿圈全程没有发生碰撞接触,直接接合. 单边碰撞,即碰撞初次发生至滑套齿进入接合之前,期间每次碰撞接触都在同一齿圈齿区间同一边倒角;多边碰撞, 即碰撞初次发生至齿接合之前,期间同一齿圈齿区间两边倒角上都有发生过碰撞接触;跨区间碰撞. 以图4(d)为例说明,初次碰撞发生在下倒角,然后滑套后退与齿圈分离,再前进碰撞时已经到达下一个齿圈齿区间,这就相当于又回到初始状态,然后依据两个部件的相对运动状态有可能经历单边碰撞、多边碰撞甚至无碰撞接合,也有可能出现多次跨区间的情况,直到完全接合. 图4 滑套与齿圈的碰撞情况分类 在实际情况中,无碰撞的出现概率比较小,而且受力简单,所以着重针对碰撞接触情况展开分析,滑套与齿圈同向旋转,在齿区间中上下倒角的碰撞接触状态有所不同,如图5所示. 图5 碰撞接触判断图 已知齿圈有N个齿,则一个齿区间所占圆周角度为2π/N. 定义Δθ为滑套位置角,其值与滑套进入齿区间的轴向相对位置Δx成正比. 当滑套与齿圈轴向相对位置为0时,Δθ=0,当滑套刚刚与齿圈接合,此时滑套与齿圈的轴向相对位置为x0且Δθ=π/N,则滑套轴向运动过程中Δθ与Δx的关系式为 (1) 定义θslv-gr为滑套和齿圈的相对转角,是转动过程中形成的,与滑套和齿圈的轴向相对位置无关,则每个齿区间内,θslv-gr的变化范围是(0,2π/N). 当滑套未越过齿圈齿尖边界线时,即Δx<0时,滑套与齿圈不会碰撞,此时处于自由行程阶段; 当0≤Δx≤x0且θslv-gr∈(0,π/N)时,则滑套与齿圈碰撞的几何条件为θslv-gr≤Δθ,属于上倒角碰撞,如图5(a)所示; 当0≤Δx≤x0且θslv-gr∈[π/N,2π/N)时,滑套与齿圈的碰撞几何条件为θslv-gr+Δθ≥2π/N,属于下倒角碰撞,如图5(b)所示; 当Δx>x0时,按照几何关系,θslv-gr恒为2π/N,即滑套的齿已经滑进齿圈的槽中间,正与齿结合. 滑套与齿圈的齿碰撞接触受力状态如图6所示. 碰撞接触面产生法向接触力Fcon和切向接触摩擦力fcon,齿圈受到由电机传递而来的驱动扭矩Tgr以及碰撞接触力;滑套除了碰撞接触力之外,还受到由地面及车轮传来的负载扭矩Tfv以及轴向推动力Fs和滑套与花键毂的滑动摩擦力fs,其中fs的方向始终与滑套轴向移动速度方向相反. 图6 碰撞接触受力示意图 碰撞过程的法向接触力模型为 (2) (3) 不同倒角碰撞接触时,相对变形ε的正向判定不同,如图7所示. 图7 接触相对变形方向判定图 (4) 上式在挂挡阶段滑套与齿圈接触的情况下才开始起作用,通过滑套的轴向位置对其进行限制. 其中rs为齿圈与滑套平均接合半径;α为齿圈齿端导角一半;s为碰撞状态系数,其表达式为 碰撞接触过程中切向接触摩擦力由法向接触力产生,已知μ为滑套与齿圈的摩擦系数,则 fcon=μFcon (5) 由图6碰撞受力分析可知,变速器内部两旋转部件接触产生的力矩Ti,slv(t)、Ti,gr1(t)和Ti,gr2(t)分别作用于滑套、一挡从动齿圈和二挡从动齿圈,则无同步器AMT挂挡碰撞接触作用阶段,三者表达式为 Ti,slv(t)=-s(fconsinα-Fconcosα)rs (6) 升挡情况下: (7) 降挡情况下: (8) 而无同步器AMT换挡过程中滑套的轴向运动方程可以统一表达为 (9) 因此,结合图8线性扭转模型图及碰撞接触示意图,接合过程中滑套与齿圈的线性动力学方程表达为 图8 传动系统线性扭转模型简化示意图 式中:Jin为变速器输入综合转动惯量;Jout为车轮-变速器输出部分综合转动惯量. 非线性扭转模型的简化示意图如图9所示,考虑变速器一挡、二挡以及主减速器斜齿轮副的啮合刚度、啮合阻尼、齿侧间隙以及静态误差等非线性因素,则一挡(i=1)、二挡(i=2)齿轮副轴向和径向啮合力为[13] 图9 传统系统非线性扭转模型简化示意图 (11) 式中:khi(t)为齿轮副啮合刚度;chi齿轮副啮合阻尼. fx(δ),fy(δ)分别为轴向和径向间隙函数,其一般表达式为 (12) (13) 式中:b为齿侧间隙;δ为动态啮合误差,则其一挡齿轮副的轴向和横向动态啮合误差分别为 δx1=x1-x4-tanβb1(r1θm+y1-r4θ4-y4)- e1(t)sinβb1 (14) δy1=r1θm+y1-r4θ4-y4-e1(t)cosβb1 (15) 二挡齿轮副的轴向和横向动态啮合误差分别为 δx2=x2-x3-tanβb2(r2θm+y2-r3θ3-y3)- e2(t)sinβb2 (16) δy2=r2θm+y2-r3θ3-y3-e2(t)cosβb2 (17) cosβb1kh1(t)fy(δy1) cosβb0kh0(t)fy(δy0) (18) 根据齿圈碰撞状态,结合图9所示的非线性模型示意图,则换挡过程中各部件非线性动力学方程可表示为 式中:rp1、rq1分别为一档齿轮副主、从动齿轮基圆半径;rp2、rq2分别为二档齿轮副主、从动齿轮基圆半径. 3.1.1换挡时间 运用matlab/simulink分别搭建线性及非线性的扭转振动模型,同时与有同步器AMT动力学模型[8]进行仿真对比,验证无同步器AMT相比有同步器AMT的换挡品质. 传动系统模型参数见表1所示[14-15],以一挡升二挡为例进行仿真分析. 表1 传动系统模型参数 换挡时间的仿真结果见表2和表3所示. 对比可知,在线性模型中,无同步器AMT比有同步器AMT的整体换挡时间缩短92.9 ms,减少了约12.5%. 在非线性模型中,无同步器AMT比有同步器的整体换挡时间缩短68.3 ms,时间减少了约7.9%. 由于无同步器换挡过程少了机械同步和拨环阶段,因此节省了时间. 说明利用无同步器AMT系统换挡可提高换挡效率. 线性和非线性模型的换挡时间差别主要发生在滑套自由行程的电机调速阶段. 表2 有同步器换挡各阶段时间 表3 无同步器换挡各阶段时间 3.1.2换挡冲击度 有同步器与无同步器AMT换挡冲击度对比,如图10、11所示. 主要的冲击度出现在摘挡完成后和挂挡齿圈碰撞开始阶段. 无同步器AMT在摘挡阶段造成的冲击度与有同步器AMT冲击度大小基本相同,但是在挂挡开始齿圈碰撞的阶段,无同步器AMT比有同步器AMT的换挡冲击度小. 在线性模型中,无同步器AMT在齿圈碰撞阶段冲击度小约0.25 m/s3. 图10 有同步器冲击度对比图 在非线性模型中,由于考虑了众多非线性因素,比如齿轮副的时变啮合刚度、齿侧间隙、啮合阻尼等,这些因素都会对变速器的齿轮副转速造成影响,从而出现冲击度的震荡现象. 为了便于对不同的模型进行比较分析,故将其拟合之后再进行对比分析. 非线性模型中冲击度减少约1.5 m/s3,相比线性模型减少的幅度,非线性模型冲击度减少的比较明显. 因此,使用无同步器AMT有利于车辆换挡品质的提高. 仿真分析分别采用100 N、150 N、200 N、300 N、500 N的轴向推动力进行分析,研究其不同大小的轴向推动力对换挡过程的影响. 仿真结果如表4所示,对于换挡时间,轴向推动换挡力越大,总的换挡时间越短. 轴向力大小主要影响空行程与挂挡阶段的时间. 当轴向推动力不断增大时,总时间减小幅度越来越小. 而换挡电机的额定功率越大,体积越大,成本越高. 因此,综合考虑换挡电机的成本、效率等因素,选择150 N大小的轴向推动力最合适. 图11 无同步器冲击度对比图 表4 无同步器AMT不同换挡力各阶段时间 不同大小轴向推动力对换挡冲击度的影响如图12所示. 轴向换挡力对冲击度的主要影响挂挡阶段中的滑套碰撞开始时期. 轴向推动力越大,挂挡开始阶段的冲击度峰值越高. 当轴向推动力为100 N时,其冲击度为2.421 m/s3. 当轴向推动力为500 N时,挂挡阶段的最大冲击度为2.822 m/s3. 当不断增加轴向力时,换挡冲击度不断增加,但是增加幅度不大,因此,结合轴向换挡力对换挡时间的影响以及电机成本等因素,适当的增加轴向换挡力,使其在一定的合适范围内,可以提高换挡品质,提升驾驶体验. 图12 不同大小轴向换挡力对冲击度的影响 本文以无同步器AMT系统为研究对象,重点分析了滑套和接合齿圈的动力学特性,定义了滑套位置角,从而通过滑套位置角来判定具体的碰撞情况. 建立了考虑啮合刚度、啮合阻尼、齿侧间隙以及静态误差等非线性因素的换挡过程动力学模型. 通过与有同步器模型的仿真对比,结果表明无同步器AMT系统比有同步器AMT系统无论在换挡品质中的换挡时间还是换挡冲击度方面都更具有优势. 同时,由于非线性因素的影响,基于非线性模型仿真分析会出现更大更复杂的冲击度,若采用线性模型控制理论的控制方法必然会造成变速箱打齿或者齿轮及滑套过早损坏的情况,从而为变速器的寿命设计、控制策略的制定等提供一定的理论指导. 通过分析不同大小轴向推动力对换挡过程的影响,选取合适的轴向推动力需要综合考虑电机成本和换挡品质等因素,为无同步器AMT系统在工程中应用提供参考. 总而言之,在纯电动车领域,无同步器AMT系统具有较大的应用前景,在设计及应用中应重点考虑滑套和齿圈接合的动力学特性,同时考虑更多的非线性因素,如路面不平度激励等对换挡过程的影响.
2 动力学建模
2.1 滑套位置角及碰撞情况分析
2.2 换挡过程动力学建模

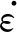




3 仿真分析
3.1 换挡品质分析

3.2 不同轴向力对换挡品质的影响


4 结 论
