黏土矿物颗粒特征对含水合物的沉积物力学特性影响研究*

韩振华 张路青 周 剑 王 颂③

(①中国科学院地质与地球物理研究所， 中国科学院页岩气与地质工程重点实验室， 北京 100029， 中国) (②北京工业大学， 北京 100124， 中国) (③中国科学院大学， 北京 100049， 中国)

0 引 言

天然气水合物是由水分子和甲烷分子在低温高压条件下形成的类冰状晶体化合物，主要分布于深海沉积物或陆域永久冻土中(Birchwood et al.，2010； Chong et al.，2016)。作为一种新型清洁能源，天然气水合物具有全球分布广、储量大、能量效率值高等特点，被认为是21世纪最有前景的替代能源之一(樊栓狮等， 2003； 李守定等， 2019)。含水合物的沉积物力学参数是水合物开发和储层稳定性评价的基础数据。由于水合物赋存的海底浅层沉积物多处于非固结状态，水合物对其有充填和胶结作用，在水合物开采过程中，水合物的分解会导致储层沉积物颗粒松散，严重时会引起钻井地层塌陷、钻井平台垮塌及海底滑坡等岩土工程问题(王淑云等， 2007； 吴能友等， 2017)。因此，准确预测储层沉积物的力学特性，可以降低上述岩土工程问题发生的可能，保障天然气水合物的安全开发，对水合物开采具有重要的参考意义。

目前，世界各国关于含水合物的沉积物力学特性的研究主要集中在室内三轴试验。由于天然气水合物极不稳定，获取含水合物的沉积物原状试样成本较高，因此，关于含水合物的沉积物力学特性的试验研究基本上是采用人工合成的试样。国内外学者利用三轴试验从不同角度研究了人工合成水合物样品的力学特征，研究大多基于砂质沉积物开展。结果表明，含水合物的沉积物力学性质受沉积物矿物颗粒本身的性质、水合物饱和度、赋存模式、围压、温度、剪切速率等多因素的影响(Hyodo et al.，2005； Masui et al.，2005； 李洋辉等， 2012； 颜荣涛等， 2013； Yun et al.，2017； Miyazaki et al.，2017)。

然而，全球天然气水合物大都赋存于海底黏土质粉砂或淤泥质沉积物中(李彦龙等， 2020)，受黏土矿物低渗透性的影响，含水合物黏土沉积物的人工样品存在制样效率低的问题，导致针对含黏土沉积物的力学性质研究较少。李令东等(2012)研究表明，采用膨润土合成的含水合物样品的力学强度要明显低于含水合物的覆膜砂样品。石要红等(2015)以我国南海粉质黏土为骨架制备含水合物的沉积物，通过三轴压缩试验得出，含水合物黏土沉积物的应力-应变曲线具有明显的应变硬化特征，这与含水合物的砂土沉积物有显著的区别。张怀文等(2017)和李彦龙等(2020)在研究含水合物的黏土质粉砂岩沉积物力学特性时，也得出了相同的结论。Wang et al. (2019)利用南海神狐海域的含黏土沉积物生成了含水合物的样品，分析了水合物饱和度和围压对沉积物力学性质的影响，结果表明，随着水合物饱和度的增加，沉积物的力学强度、刚度、内摩擦角和黏聚力都会显著提高。王淑云等(2018)研究得出，含水合物的黏土沉积物不排水抗剪强度要比不含水合物的黏土强度高1～6倍。Wang et al. (2020)也利用不排水三轴剪切试验研究了含水合物的粉质黏土的力学特性，研究表明，样品的内摩擦角随水合物饱和度的增加而增大，但内摩擦角与水合物饱和度没有相关性。

采用室内试验研究含水合物的沉积物力学特性时，由于缺乏统一的制样标准和试验方法，造成试验结果差异很大，并且试验获取的信息也有限，难以揭示复杂宏观现象的微观机理。因此，一些学者通过离散元模拟来研究含水合物的沉积物的力学特征(程升等， 2018)。Jung et al. (2012)利用颗粒流程序PFC研究了水合物的分布形式对模型宏观力学行为的影响。蒋明镜等(2014)将纯水合物视为由大量颗粒胶结而成的块体，利用三维离散元模拟对颗粒间的微观参数进行了反演。Yu et al. (2016)基于DEM的三轴排水剪切模拟试验，分析了颗粒形状、水合物赋存方式及饱和度对含水合物的沉积物力学行为的影响。

我国南海神狐海域钻探的沉积物中含有大量的黏土(图 1)。由于黏土与砂土的力学性质差异明显，所以黏土矿物组分必然会对沉积物的力学行为造成显著影响。当前研究已证明了含水合物的黏土沉积物与砂土沉积物在力学特性上有明显区别，但研究大多集中于水合物饱和度和围压等外界因素的影响，针对黏土颗粒本身性质对沉积物力学行为影响的试验和模拟研究文献尚很少见。由于矿物颗粒本身的性质是影响沉积物力学性质的基础因素，所以从矿物颗粒特征出发开展含黏土沉积物力学性质的研究非常必要。本次研究从矿物颗粒特征的角度出发，基于PFC离散元模拟，首先分析了黏土矿物的含量、形状、颗粒排列等因素对不含水合物的沉积物三轴压缩力学特性的影响，然后考虑水合物对矿物颗粒的胶结作用，进一步分析了矿物颗粒间的胶结程度和围压对含水合物的沉积物三轴压缩力学特性的影响，相关成果可为我国南海神狐海域含水合物的沉积物强度及变形特征分析提供依据。

图 1 我国不同海域的天然气水合物样品(刘昌岭等， 2017)Fig. 1 Natural gas hydrate samples from different sea areas in China(Liu et al.，2017)a. 取自南海神狐海域的样品； b. 取自珠江口盆地东部海域的样品

1 颗粒流分析法的基本原理

颗粒流分析法是一种非连续数值计算方法，适用于分析准静力和动力条件下的材料力学问题。该方法用颗粒集合体来表征物体，以牛顿第二定律和力-位移定律为基础，通过模拟颗粒单元的运动和相互作用来反映物体的宏观本构行为(Cundall， 1971)。颗粒流分析法的基本计算原理为：(1)根据颗粒单元间的接触力，采用牛顿第二定律计算每个颗粒的位移、速度和加速度，更新颗粒的位置； (2)根据颗粒的位移等特征，采用力-位移定律更新颗粒单元间的接触力。循环上述计算，直到模型破坏或满足设定条件，计算结束(韩振华等， 2019)。

颗粒流分析法常用的基本接触模型有3种：接触刚度模型(线性模型和Hertz-Mindlin模型)、滑动模型和黏结模型(点接触黏结模型和平行黏结模型)。其中：接触刚度模型主要体现单元间法向、切向接触力与法向、切向相对位移的关系(图 2a)，常用来模拟散体材料的力学行为。平行黏结模型假设颗粒间存在胶结聚合物，胶结物质具有一定的强度，允许产生一定的变形，并且可以传递颗粒之间的力和力矩(图 2b)。

图 2 颗粒和平行黏结的受力-位移关系(Han et al.， 2019)Fig. 2 Force-displacement behavior of the grain and the parallel bond(Han et al.，2019)a. 接触刚度模型； b. 平行黏结模型

2 模型建立及参数标定

2.1 模型建立

本次研究拟采用三轴压缩试验来分析含水合物的沉积物力学特性。利用PFC模拟样品三轴压缩时，首先要生成模型的4个墙体，确定模型边界，然后利用伺服调节法控制模型的“墙体”运动，模拟加载过程。模型尺寸采用10 mm×5 mm，模型的矿物组分参考我国南海神狐海域的沉积物进行建立。张辉等(2016)对南海北部神狐海域沉积物颗粒粒径进行了统计(图 3)，发现沉积物主要成分为粉砂(4～63 μm， 65%～78.6%)，次要组分为黏土(<3.9 μm， 12.8%～24.2%)或砂(>63 μm， 4.6%～21.3%)。若采用南海神狐海域沉积物的粒径建立模型，模型中的颗粒数量将超过软件的计算上限，故本次研究对矿物组分和粒径进行了简化，设定模型中黏土的含量为20%，砂土含量为80%。黏土颗粒最小半径0.03 mm，砂土颗粒最小半径0.05 mm，粒径比选均为1.66，颗粒粒径服从正态分布，共生成约4300个颗粒，最终生成模型的孔隙率为15.2%。由于PFC模型中的颗粒处于一种较密实的排列状态，因此模型孔隙率要低于实际含水合物的沉积物样品。

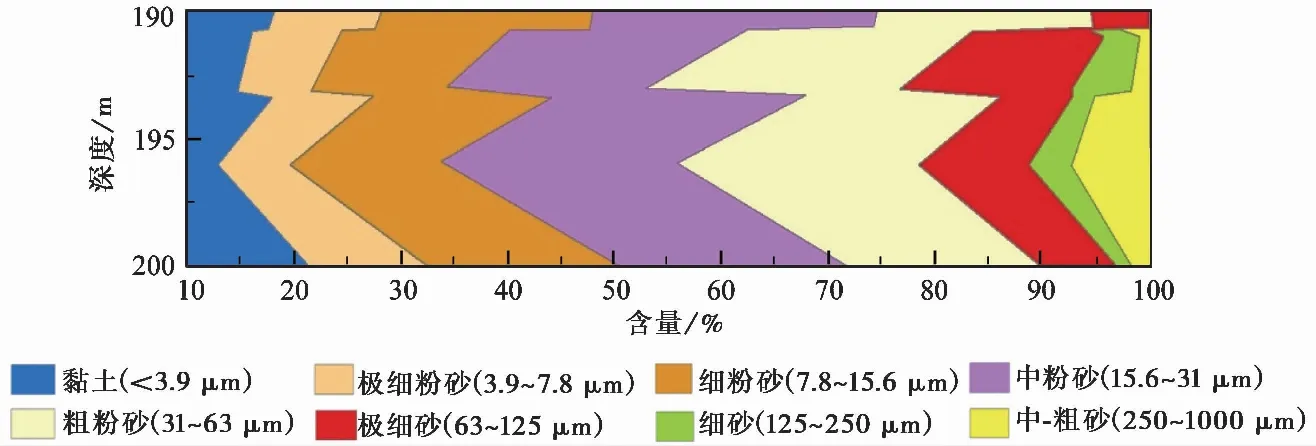
图 3 南海神狐海域沉积物的颗粒组分分布(张辉等， 2016)Fig. 3 The grain size distribution of sediments from Shenhu area of South China Sea(Zhang et al.，2016)

2.2 细观参数标定

针对不含水合物的沉积物模型，采用散体材料，即不考虑颗粒的胶结作用，模型内所有颗粒间的接触均采用简单的线弹性接触。颗粒的主要细观参数有弹性模量、法向与切向刚度的比值(刚度比)和摩擦系数(表 1中的颗粒部分)。当模型中考虑水合物时，沉积物孔隙中不同赋存形式的水合物(图 4)对沉积物力学特性的影响也不同。本次研究主要考虑了胶结型水合物(图 4c)，采用平行黏结模型(图 2b)，通过设置颗粒间的黏结来体现水合物的胶结作用。

表 1 PFC三轴压缩试验模型细观参数Table 1 Micro mechanical parameters of numerical model

图 4 水合物在沉积物孔隙中的3种主要赋存形式Fig. 4 Three main distribution forms of hydrate in sedimentsa. 填充模式； b. 持力体模式； c. 胶结模式

平行黏结的主要细观参数有强度、弹性模量、刚度比和半径乘子(表 1所示的平行黏结部分)。其中：半径乘子λ决定平行黏结的长度，如式(1)和图 5所示，半径乘子λ取值范围为0～1。当λ取1时，黏结长度最大(为两侧接触颗粒的最小直径)，当λ取0时，颗粒间无黏结作用。平行黏结的长度在一定程度上可以代表水合物的含量及其对颗粒的胶结程度，半径乘子λ值越大，水合物含量越大，颗粒间的胶结作用越强。

R=λ· min(RA，RB)

(1)

式中：R为平行黏结长度；RA和RB表示黏结两侧颗粒的直径。模型的参数值主要采用“试错法”进行确定，即反复改变细观参数，使得模型的宏观力学参数(峰值强度、弹性模量、泊松比等)与试验结果或经验值接近。其中：峰值强度主要受黏结强度和颗粒摩擦系数的影响，弹性模量主要受颗粒和黏结模量的影响，泊松比主要受刚度比影响。设置模型围压为1 MPa，调整细观参数，使得模型的宏观力学参数接近试验结果，最终确定的模型细观物理力学参数如表 1所示。

图 5 颗粒间胶结程度与半径乘子关系示意图Fig. 5 Relationship between the interparticle cementation degree and radius multiplier

当试验有效围压为1 MPa时，表 2给出了几个针对含黏土沉积物力学参数的试验结果。可以看出，几个试验结果也存在明显的差异，主要原因为含水合物的沉积物力学性质受多种因素的共同影响，不同的试验很难保证各变量的相同。本次参数标定中，随着平行黏结半径乘子的增大，即水合物含量的增大，模型的强度和模量均增大。强度的变化范围与已有试验结果接近，初始切向模量的变化范围要比试验结果大。主要原因为，本次模拟采用的水合物赋存方式是胶结模式，而人工合成的水合物样品中，水合物赋存方式也包含充填和持力体等模式，而胶结模式的水合物对沉积物模量具有显著提高作用(颜荣涛等， 2013)。当水合物饱和度小于20%时，水合物为胶结模式的沉积物模量要比充填或持力体模式的沉积物模量提高近400 MPa。数值模型应力-应变曲线特征、各宏观参数随黏结半径乘子的变化规律将在下文作进一步分析。

表 2 模型细观参数标定结果与试验结果对比Table 2 Micro mechanical parameters comparison of calibration results and test results

3 研究方案设计

本次研究内容主要为黏土矿物粒径特征对沉积物宏观力学特性的影响。首先考虑了黏土矿物的含量、形状、颗粒排列等因素对不含水合物的沉积物三轴压缩力学特性的影响，设计了3种研究方案，模型的细观参数采用表 1所示的颗粒部分，颗粒间无黏结。其次，考虑了水合物的胶结作用对含水合物的沉积物三轴压缩力学特性的影响，设计了1种研究方案，颗粒间设置平行黏结。共4种计算方案(表 3)，具体如下：

表 3 4种研究方案设计Table 3 Four scenarios with different mineral grain characteristics and confining pressure

3.1 针对不同黏土矿物含量的模型设计

本次研究共设计了6种不同的黏土矿物含量，以分析黏土矿物组分对沉积物力学特性的影响，黏土矿物含量分别设定为： 0， 10%， 20%， 30%， 40%， 50%，模型围压设置为1 MPa。

3.2 针对不同黏土矿物颗粒形状的模型设计

由于黏土中存在大量针状或片状的次生矿物，采用传统的圆形颗粒体模型无法反映黏土颗粒的形状效应。因此，本次研究利用PFC提供的“CLUMP”方法构建条形颗粒。该方法是将多个圆形颗粒组合形成一个整体，建模过程中，首先生成圆形颗粒集合体，然后用条形颗粒将其替换，条形颗粒与被替换的圆颗粒面积相等、面积中心一致且排列方向随机。以颗粒的长短轴之比(Se)来对黏土颗粒形状进行定量描述，共建立了6种长短轴比不同的条形颗粒，如图 6所示，颗粒长短轴Se分别为1、1.5、2.0、2.5、3.0、3.5，模型围压设置为1 MPa。

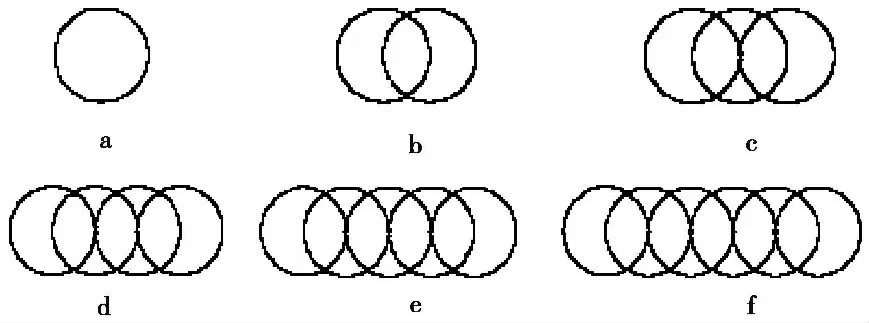
图 6 条形黏土矿物颗粒单元Fig. 6 Striped clay mineral grain unita. Se=1.0； b. Se=1.5； c. Se=2.0;d. Se=2.5; e. Se=3.0; f. Se=3.5

3.3 针对不同黏土矿物颗粒方向的模型设计

在深海沉积物中，由于海水的流动都具有较强的方向性，所以黏土矿物颗粒在沉积过程中也具有一定的方向性。为了研究黏土矿物颗粒排列对沉积物力学特性的影响，需指定条形颗粒的排列倾角β，本次研究采用长短轴比Se为3.0的模型(图 6e)，共设计了4种排列倾角形式： 0°、30°、60°、90°，模型围压设置为1 MPa。

3.4 针对颗粒间不同胶结程度的模型设计

本次研究共设计了6种粒间胶结程度不同的模型，半径乘子λ分别取值为： 0、0.2、0.4、0.6、0.8、1.0。此外，由于围压也是影响含水合物的沉积物力学特性的重要因素，因此，本方案设置了3种围压状态，分别为1 MPa、2 MPa、5 MPa，来研究不同围压条件下颗粒的胶结程度对含水合物的沉积物的影响。

4 矿物颗粒特征的力学效应分析

本次设计的4种研究方案综合考虑了黏土矿物含量、颗粒形状、颗粒排列、颗粒胶结程度及围压的影响。根据三轴压缩模拟结果主要分析了上述因素对沉积物强度、弹性模量、泊松比、变形破坏等特性的影响。

4.1 黏土矿物含量对沉积物力学性质影响分析

对于方案1中的5种黏土矿物含量不同的模型，在三轴压缩模拟过程中的偏应力-应变曲线如图 7所示。根据模拟得出的偏应力-应变曲线可确定模型的峰值强度、弹性模量、泊松比等宏观力学参数，如图 8所示。

图 7 方案1中不同黏土矿物含量模型的偏应力-应变曲线Fig. 7 Deviatoric stress-strain curves of numerical models with different clay mineral content in scenario 1

图 8 方案1中黏土矿物含量对模型宏观力学参数的影响(围压1 MPa)Fig. 8 Effects of clay mineral content on model mechanical properties in scenario 1(confining pressure of 1 MPa)a. 峰值强度； b. 弹性模量; c. 泊松比

由图 7和图 8可以看出，当黏土矿物含量小于30%时，随黏土矿物含量的增大，模型的峰值强度呈明显降低的趋势； 黏土含量大于30%后，峰值强度降低的幅度逐渐减小。峰值强度的变化范围为1.5～2.2，降低约32%。模型弹性模量的变化规律与峰值强度类似，变化范围为454～243 MPa，降低约46%。模型的泊松比受黏土含量影响不大，变化范围为0.24～0.28。已有研究表明，当沉积物中含水合物时，水合物对矿物颗粒有胶结作用，但随着开采过程中水合物的分解，沉积物本身的强度则直接影响储层的稳定性。根据模拟结果，沉积中的黏土组分对储层力学参数有显著降低作用，我国南海含水合物的地层主要为粉质黏土，因此，黏土组分对开采过程中储层稳定性的影响值得关注。

4.2 黏土矿物颗粒形状对沉积物力学性质影响分析

对于方案2中的6种黏土矿物颗粒形状不同的模型，图 9给出了黏土矿物颗粒形状对其峰值强度、弹性模量和泊松比的影响。由图 9a可以看出，模型的峰值强度随黏土颗粒长短轴比的增大呈现先增长后降低的规律，相比于圆颗粒(Se=1)，黏土矿物采用条形颗粒(Se>1)时，模型的峰值强度提高约70%，当Se=2时模型峰值强度达到最高，随后缓慢下降，弹性模量也表现出了相同的规律(图 9b)。由图 9c可以看出，条形颗粒模型的泊松比较圆颗粒模型明显降低，但几个条形颗粒模型的泊松比没有明显变化。

图 9 方案2中黏土矿物形状对模型宏观力学参数的影响(围压1 MPa)Fig. 9 Effects of clay mineral grain shape on model mechanical properties in scenario 2(confining pressure of 1 MPa)a. 峰值强度; b. 弹性模量; c. 泊松比

已有研究表明，颗粒形状对试样力学行为的影响在细观机理上与颗粒平均接触数量相关(史旦达等， 2008)。图 10给了颗粒初始平均接触数量与颗粒形状的关系，可以看出，黏土矿物采用条形颗粒时，颗粒的接触数量要明显高于圆形颗粒。因此，相比于圆形颗粒，条形颗粒间的咬合作用高，颗粒的旋转量也小，颗粒整体结构更稳定，在外力作用下模型变形小，模型的峰值强度和弹性模量均高于圆形颗粒体模型。赵洲等(2019)基于离散元分析了颗粒形态对软黏土抗剪强度的影响，也得出了相似的结论。

图 10 黏土矿物形状与颗粒平均接触数量的关系Fig. 10 Relationship between the clay mineral shape and the average contact number of grains

由图 10还可以看出，颗粒初始平均接触数量随黏土颗粒长短轴比Se的增大也呈现先增长后降低的规律，当Se=2时颗粒初始平均接触数量达到最高，颗粒初始平均接触数量与模型的峰值强度和弹性模量有良好的正相关关系。

4.3 黏土矿物颗粒排列对沉积物力学性质影响分析

对于方案3中的4种黏土矿物颗粒排列不同的模型，图 11给出了颗粒胶结程度对其峰值强度、弹性模量和泊松比的影响。可以看出，模型的峰值强度随黏土颗粒倾角的增大呈降低的趋势。弹性模量随黏土颗粒倾角的增大呈先降低后增大的趋势，在黏土颗粒倾角为30°时达到最低值。泊松比随黏土颗粒倾斜角的增大而增大，但增长幅度很小。

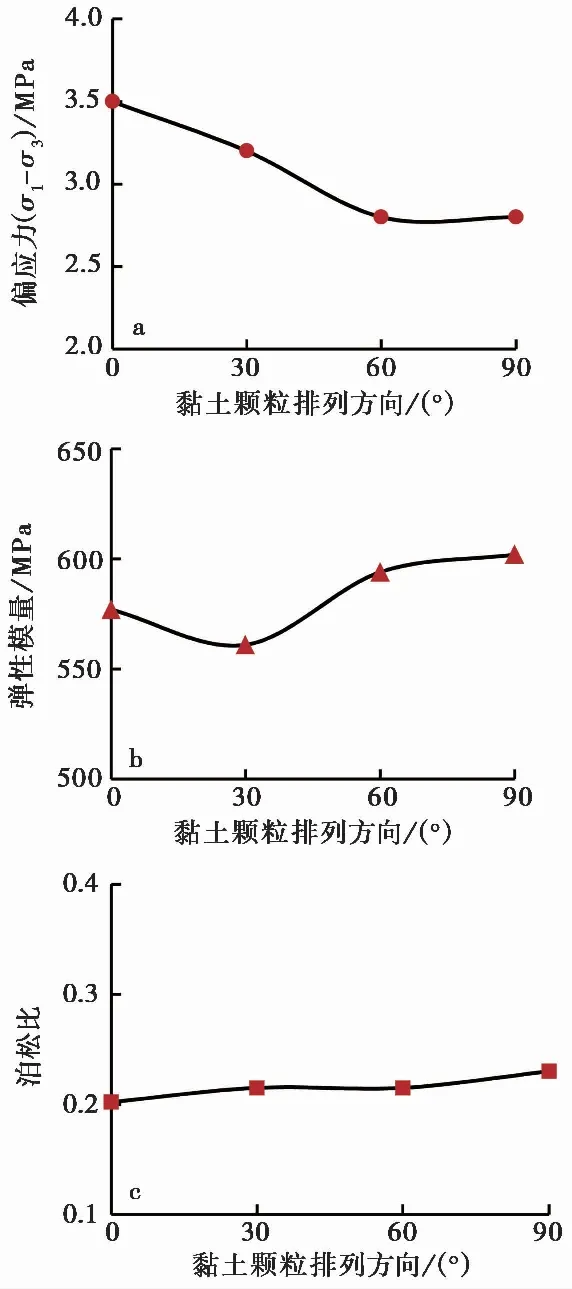
图 11 方案3中黏土矿物颗粒方向对模型宏观力学参数的影响(围压1 MPa)Fig. 11 Effects of clay mineral grain arrangement on model mechanical properties in scenario 3(confining pressure of 1 MPa)a. 峰值强度; b. 弹性模量; c. 泊松比

模型峰值强度随颗粒倾角的变化与黏土颗粒的受力状态相关。当黏土矿物颗粒接近水平排列时，轴压方向与颗粒排列方向垂直，颗粒上下层之间交错排列，在水平方向上的颗粒接触数量多(图 12a)，颗粒结构比较稳定，因此，模型的峰值强度高。当黏土矿物颗粒接近垂直排列时(图 12b)，颗粒沿长轴方向受力，黏土颗粒的接触点位于其长轴端部，在轴压方向接触数量少，颗粒结构不稳定，因此，模型峰值强度较低。弹性模量是模型弹性变形难易程度的表征，在相同的轴压条件下，模型在弹性范围内越容易发生变形，弹性模量越小。PFC程序假设颗粒单元为刚体，允许在颗粒接触处发生微小变形。当黏土矿物颗粒接近垂直排列时，沿轴压方向颗粒接触界面最少，相应的变形也最小，因此模型的弹性模量最高。随着颗粒排列倾角的减小，颗粒单元之间的接触界面沿轴向逐渐增多，因此弹性模量逐渐降低。

图 12 不同黏土矿物颗粒排列下模型内部接触应力分布(以β=0°和90°模型为例，蓝色：黏土颗粒，黄色：砂颗粒)Fig. 12 Distribution of the contact force under different clay grains arrangementa. β=0°; b. β=90°

4.4 矿物颗粒胶结程度对沉积物力学性质影响分析

对于方案4中的6种颗粒胶结程度不同的模型，在围压为1 MPa、2 MPa和5 MPa时，模型在三轴压缩模拟过程中的偏应力-应变曲线如图 13所示。可以看出，颗粒胶结和围压对模型力学特性有显著影响。

图 13 方案4中不同围压下6种颗粒胶结程度模型的偏应力-应变曲线Fig. 13 Deviatoric stress-strain curves of models with different interparticle cementation degree and confining pressure in scenario 4

当模型围压一定时，随着颗粒间平行黏结半径乘子λ的增大，即颗粒间胶结程度的增强，模型的峰值强度和弹性模量呈明显增长的趋势。以围压2 MPa的模型为例，图 14给出了颗粒胶结程度对模型峰值强度、弹性模量和泊松比的影响，其中：峰值强度增长116%，弹性模量增长161%，泊松比随颗粒间胶结程度的增强呈降低趋势，降低约45%。当颗粒间胶结程度一定时，(以λ=0.6的模型为例)，模型在不同围压作用下的偏应力-应变曲线如图 15所示，可以看出，随着围压的增加，模型的峰值强度也有明显增加，弹性模量也有所提高，但幅度不大，围压对泊松比无明显影响。由于水合物对矿物颗粒有明显的胶结作用，水合物饱和度越大，对颗粒的胶结作用越强。大量试验结果已表明，含水合物的沉积物的强度和弹性模量随水合物饱和度和围压的增大而增大(Wang et al.，2019； 李彦龙等， 2020)，但泊松比受其影响较小(Masui et al.，2005； 李令东等， 2012)。因此，本次研究采用平行黏结来表征水合物的胶结作用，并用黏结长度来反映颗粒间的胶结程度，也能模拟水合物饱和度和围压对模型宏观力学参数的影响规律。

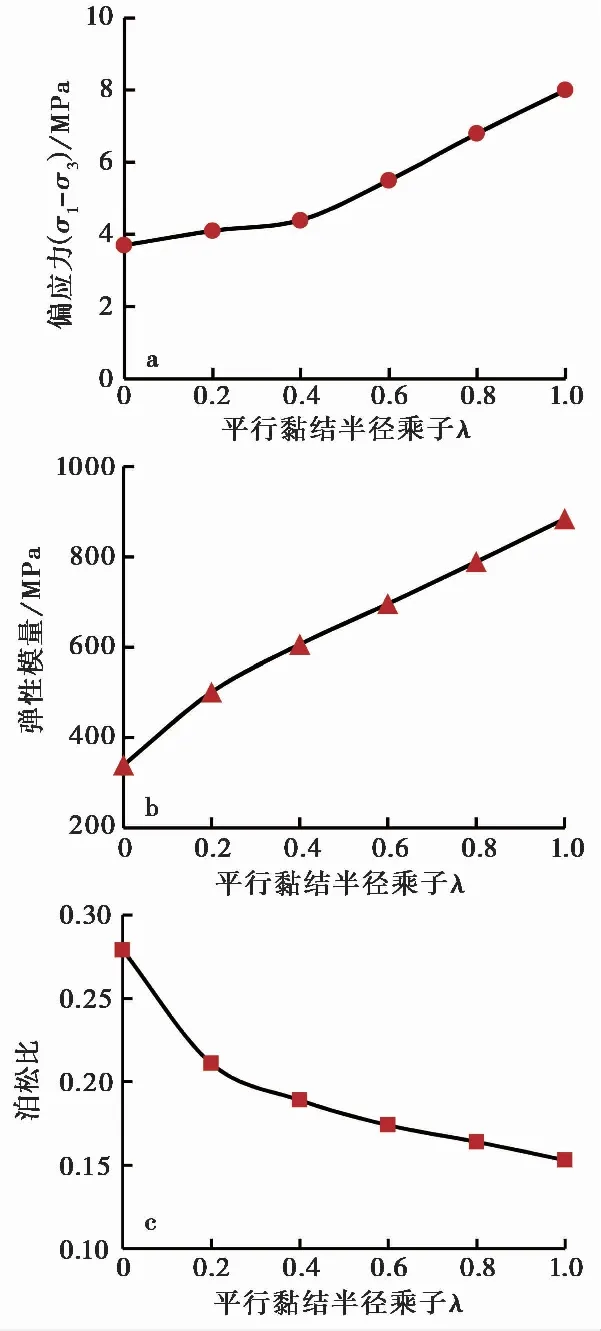
图 14 方案4中颗粒胶结程度对模型宏观力学参数的影响(围压2 MPa)Fig. 14 Effects of interparticle cementation degree on model mechanical properties in scenario 4(confining pressure of 2 MPa)a. 峰值强度; b. 弹性模量; c. 泊松比

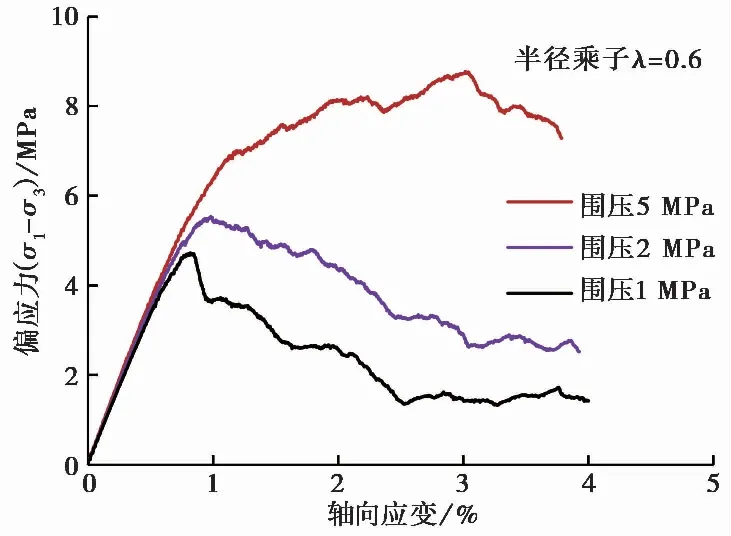
图 15 黏结半径乘子为0.6时不同围压下模型的偏应力-应变曲线Fig. 15 Deviatoric stress-strain curves of model with radius multiplier of 0.6 under different confining pressure

研究还表明，颗粒的胶结程度和围压对模型破坏方式也有显著影响。图 16给出了围压为2 MPa时颗粒胶结程度不同模型的裂纹分布。在PFC程序中，当颗粒间接触力超过黏结强度时，黏结破坏，即产生一个微裂纹。可以看出，当λ=0时，颗粒间无黏结，模型未发育裂纹。当λ大于0时，随着颗粒胶结程度的增强，模型中的微裂纹数量逐渐减少，宏观裂缝逐渐沿模型对角贯通。结合图 13可以看出，当颗粒胶结程度较低(黏结半径乘子λ小于0.4)时，模型的偏应力-应变曲线表现为应变硬化的特征，无明显的峰值点，模型破坏方式为塑性破坏。当颗粒胶结程度较高(黏结半径乘子λ大于0.4)时，在低围压状态下，模型的偏应力-应变曲线表现出应变软化的特征，达到峰值点后有很明显的应力降，模型破坏方式为脆性破坏。由图 13和图 15还可以看出，随着围压的增加，峰值点后的应力降逐渐减小，且屈服阶段变长，模型逐渐由脆性破坏向塑性破坏转换。模型的破坏方式可总结为，当颗粒间胶结程度低，模型为塑性破坏，当颗粒间胶结程度强时，模型在低围压状态下为脆性破坏，在高围压状态下为塑性破坏。

图 16 围压2 MPa时6种颗粒胶结程度不同模型的破裂形态(黑色：张拉裂纹； 红色：剪切裂纹)Fig. 16 Failure mode of the models with different interparticle cementation degree(black： tensile cracks， red： shear cracks)a. λ=0; b. λ=0.2; c. λ=0.4; d. λ=0.6; e. λ=0.8; f. λ=1.0

进一步将模拟结果与表 2所示的试验结果进行了对比分析。结果表明，当颗粒胶结程度较低，即水合物饱和度低时，模拟出的应力-应变曲线与实验结果相似(Wang et al.，2019； 李彦龙等， 2020)，表现出了应变硬化的特征。张怀文等(2017)试验结果表明，样品中水合物饱和度较高且围压较低时，样品强度在达到峰值点后存在应力降，但模拟结果的应力降要明显高于试验结果。主要原因为，首先在PFC模拟中采用的是圆形颗粒，颗粒间的咬合作用小，且粒间胶结破坏后，颗粒间只有简单的线性接触，故峰值点后应力下降迅速(蒋明镜等， 2014)。而实际沉积物中颗粒形状复杂、表面粗糙，即使粒间黏结被破坏，颗粒间的咬合作用也能抵抗一定的压力。其次，模型孔隙率要明显低于实际含水合物的沉积物样品，因此，数值模型的应力-应变曲线反映出密实试样的软化现象，而实际模型孔隙率较大，应力-应变曲线则呈现出硬化现象。此外，随水合物含量的增大，胶结型含水合物沉积物的应力-应变曲线也通常会呈现应变软化特征。

5 结 论

本文从矿物颗粒特征出发，基于颗粒流程序PFC，分析了黏土矿物的含量、形状、排列对不含水合物的沉积物及颗粒胶结程度、围压对含水合物的沉积物三轴压缩特性的影响，根据模拟结果，得到的主要结论如下：

(1)当模型中不含水合物时，黏土矿物含量的增多对模型的力学强度和弹性模量有明显降低作用，黏土含量大于30%后，峰值强度降低的幅度减小。

(2)相比于圆形颗粒模型，黏土矿物采用条形颗粒时，模型的峰值强度提高约70%，弹性模量提高约80%，颗粒长短轴比为2的模型强度和弹性模量最高。颗粒长短轴比影响颗粒初始平均接触数量，进一步影响模型宏观参数，强度高的模型初始平均接触数量也高。

(3)条形黏土颗粒的排列方向对模型力学参数也有明显影响。峰值强度均随颗粒倾角增大呈降低趋势，弹性模量均随颗粒倾角增大呈先减小后增大的趋势，黏土颗粒倾角为30°时达到最低。

(4)当模型中考虑水合物对颗粒的胶结作用后，在相同围压下，模型的峰值强度和弹性模量随着颗粒间胶结程度的增强明显增大。相同颗粒胶结程度下，随着围压的增加，模型的峰值强度也明显增加，弹性模量也有所提高。

(5)颗粒的胶结程度和围压对模型破坏方式影响显著，随着颗粒胶结程度的增大和围压的减小，模型偏应力-应变曲线由应变硬化向应变软化转换，破坏方式由塑性破坏向脆性破坏转换。