考虑海水-海床耦合效应的海底隧道地震响应研究*

陈炜昀 吕振宇 徐令宇 阮 滨 马建军 陈国兴

(①南京工业大学， 岩土工程研究所， 南京 210009， 中国) (②中山大学， 土木工程学院， 广州 510275， 中国) (③华中科技大学， 土木与水利工程学院， 武汉 430074， 中国)

0 引 言

近些年来，国内外海底隧道的建设发展迅速，中国已经成为了全球发展最快的隧道建设市场。海底隧道具有不受天气影响、通过量大、结构稳定性好等优点，但是其建造难度大，技术复杂(唐少辉等， 2020)，造价高昂，且大多建立在地震频发的沿海地区，这对于海底隧道的抗震设计提出了更高的要求。海底隧道所面临的海洋地质环境复杂，相比于陆地隧道而言，除了周围海底岩土体的物理力学性质不同，上覆海水的存在也会对海床及海床内结构物产生影响(刘勇等， 2013)，因此在进行海底隧道抗震研究时需要考虑上覆海水与地震的耦合作用对于海底隧道响应的影响。

目前，关于陆上地下结构的研究已较为成熟(高广运等， 2019； 徐强等， 2020； 尚彦军等， 2021)，海底隧道相关的研究还是较少，主要集中在理论分析、试验研究和数值模拟3个方面。在试验方面，袁勇等(2016)以港珠澳大桥为背景建立了超长沉管隧道的多点振动台模型，研究了非一致地震激励下沉管隧道的响应。程新俊等(2020)根据某超长沉管隧道，建立了饱和砂土中的多段式沉管隧道振动台模型，以此研究了沉管隧道在饱和砂土场地中的地震反应规律。崔杰等(2020)分别设计了有无上覆水作用的沉管隧道振动台试验，并将试验结果与数值计算结果进行对比验证，指出上覆水的存在会使场地加速度放大系数变小并且隧道应力随着水深增加而增加。在理论研究方面，朱镜清(1988)针对地震作用下海水与海床土耦合运动的一维情形作了力学分析，建立了相应的数学模型，但并没有考虑结构物的影响。朱赛男等(2020)在Biot流体饱和多孔介质和理想流体介质波动理论的基础上，采用Hankel函数积分变换法，在水-土-结构相互作用的条件下，得到了海底衬砌隧道对平面P波散射问题的解析解，并在此基础上计算分析了各种因素对海底衬砌隧道地震响应的影响。目前对于海底隧道地震响应分析的研究大多还是集中在数值模拟方面上，相比于其他分析方法，数值方法在费用、操作性、计算区域大小与模型复杂程度上更具优势。刘勇等(2013)、张如林等(2014)、Miao et al. (2018)、陈国兴等(2019)分别使用数值模拟方法建立了相应的海底隧道模型，研究了地震作用下海底隧道结构的动力响应规律。值得注意的是，过去的研究大多不考虑海水影响，或仅将上覆水压力以荷载形式施加，忽略了水-土动力相互作用，显然不尽合理。Zeinoddini et al. (2012)使用声-固耦合法实现了海底悬跨管道的水-管道动力相互作用，并与附加质量法进行对比验证，研究表明附加质量法较声-固耦合法更保守，在地震激励时两种方法的差异约为15%的结论。Cheng et al. (2018)以青岛胶州湾海底隧道为背景，采用谐波模拟海浪，以此研究了海底隧道在海浪和地震共同作用下的动力响应规律，发现海浪对于隧道应力影响较大并且在水深超过40 m后可以不用考虑海浪影响。Shekari (2021)通过将压力作为独立节点变量来表示流体流动效应，实现了二维流-固耦合模型，强调了地震动频率的重要性，指出隧道的整体地震响应由地震频率成分决定。

本文以某海峡海底隧道工程为案例，针对埋深较浅，在地震作用下受动水压力影响较大的海底隧道，不同于埋深较大的海底隧道。基于ABAQUS有限元软件，利用声-固耦合方法模拟海水-海床之间的动力相互作用，结合黏弹性人工边界，并考虑海床沉积土体的非线性特征，最终建立海水-海床-隧道全耦合数值分析模型。通过参数分析，研究了海底隧道在不同地震动输入、不同地震激励方向及不同上覆水深条件下的隧道响应规律。

1 数值分析方法

1.1 土体非线性本构模型

采用基于Davidenkov骨架曲线、不规则加卸载准则构造的Non-Masing本构模型(赵丁凤等， 2017)描述海床土体的非线性应力-应变关系，以自定义子程序模块嵌入ABAQUS软件。该模型适用于场地非线性地震效应分析，能够较为理想地描述各类土体的非线性动力特性(龚彩云等， 2018； 王杰等， 2020； Chen et al.，2020， 2021； 陈国兴等， 2021)。Davidenkov骨架曲线的表达式为：

τ=Gγ=Gmaxγ[1-H(γ)]

(1)

其中：

(2)

式中：τ，γ分别为剪应力和剪应变；Gmax为初始剪切模量；A、B和γ0为土的试验参数。

1.2 流-固耦合方法及其验证

采用声学模块单元来模拟流体，进而模拟海水与海床之间的动力相互作用，动水压力pw的控制方程如下：

(3)

式中：t为时间；2为二维拉普拉斯算子；c为流体声速；为液体的体积模量。相较于其他方法，声-固耦合方法计算简单高效，它假设模型中没有材料流动从而没有网格变形并且声学单元仅在每个节点上具有压力自由度，因此它能大大减少仿真计算时间，但因为声学单元只有压力自由度，因此不能显示出海水的位移变化(Rawat et al.，2019)。

通过与解析解对比，对声-固耦合模拟方法的准确性进行验证。首先建立了库水-大坝的耦合模型，整体尺寸及网格划分如图 1a 所示。重力坝的密度为2400 kg · m-3，弹性模量为2.8×105GPa，泊松比为0.167，大坝高度105 m，宽度为70 m，水的密度为1000 kg · m-3，体积模量为2.04 GPa，库水高度为100 m，宽度300 m。作为对比的解析解，这里采用的是Westergaard(1933)推导的垂直刚性表面受到水平加速度时的动水压力的解，具体公式如下：

(4)

其中

(5)

式中：H为水库的深度；h为从自由表面算起的深度；Tg为加速度周期； üg为地面加速度。从大坝底部输入水平正弦波激励，输入激励波如图 1b 所示。在模型中提取了坝体中部和底部点的动水压力时程数据以及沿坝面高度分布的最大动水压力分布，图 1c和图 1d 展示了从大坝各种位置提取的计算结果和Westergaard公式计算结果的对比。可见，在整个计算过程中，数值结果与Westergaard解析解高度吻合，验证了声学单元模拟水-结构的动力相互作用的准确性。

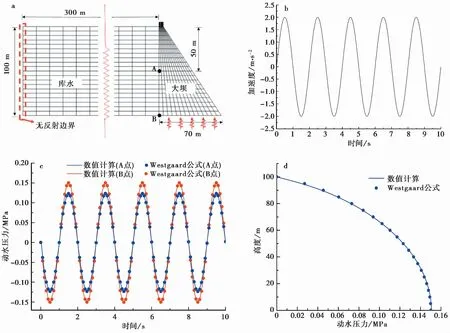
图 1 流-固耦合模型示意图及数值结果与解析解对比Fig. 1 Schematic diagram of fluid structure coupling model and comparison between the numerical and analytical resultsa. 水库大坝示意图及网格划分; b. 输入激励; c. 底部动水压力对比; d沿高度最大动水压力对比

1.3 混凝土本构

采用ABAQUS内置的混凝土塑性损伤模型(CDP)来描述混凝土材料的应力特性，混凝土在弹性受力阶段，CDP模型直接通过初始弹性模量对材料进行计算，材料在进入损伤阶段之后，弹性模量相应调整为(张飞等， 2021)：

E=(1-d)E0

(6)

式中：E为弹性模量；E0为初始弹性模量；d为损伤因子，取值范围为0≤d≤1，0代表混凝土不发生材料损伤， 1代表混凝土发生完全损伤，完全丧失强度。模型中的混凝土损伤参数根据GB50010-2010规范计算所得。

2 海底隧道数值模型的建立

本文以某海峡海底隧道工程为案例进行模型建立，根据海底隧道的埋深与场地水深范围，将海底隧道模型的埋深和上覆海水深度分别设置为20 m和35 m作为基本分析模型。隧道管环外径为14 m，内径为12.8 m，衬砌厚度0.6 m，隧道的混凝土强度等级为C60，采用混凝土塑性损伤模型(CDP)描述，本构参数如表 1 所示。计算区域的长度取为300 m，深度取为100 m，土体本构采用基于Davidenkov骨架曲线、不规则加卸载准则构造的Non-Masing本构模型，结构和土体的计算单元均采用CPS4R实体计算单元，土体参数如表 2 所示。

表 1 混凝土损伤模型参数

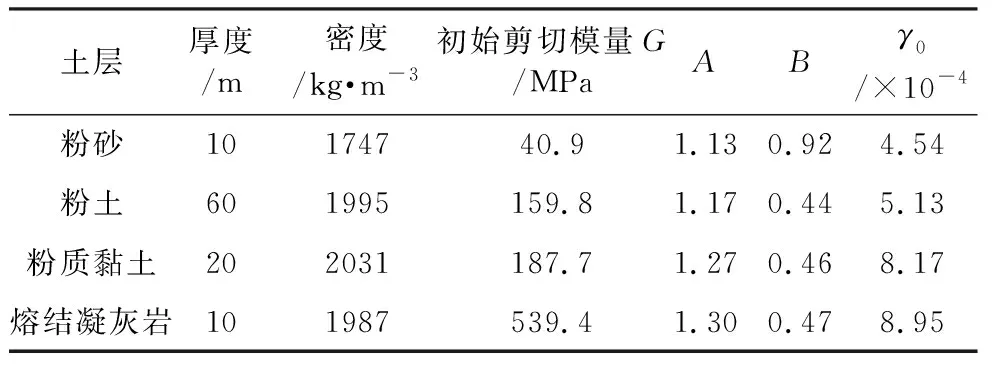
表 2 海床土的本构模型参数Table 2 Parameters of the constitutive model of the subsea soils

上覆海水用AC2D4R声学单元计算，水的密度为1000 kg · m-3，体积模量为2.04 GPa。对整体模型网格划分进行局部精细化处理，将隧道附近区域网格进行加密，以此获得更准确的结果同时减少计算时间，具体网格划分及模型尺寸划分示意图如图 2 所示。隧道和土体之间采用面面接触，摩擦系数取为0.3，在土体边界设置黏弹性人工边界(刘晶波等， 2006)，海水边界设置无反射边界，以此实现对侧边界无限域的模拟。

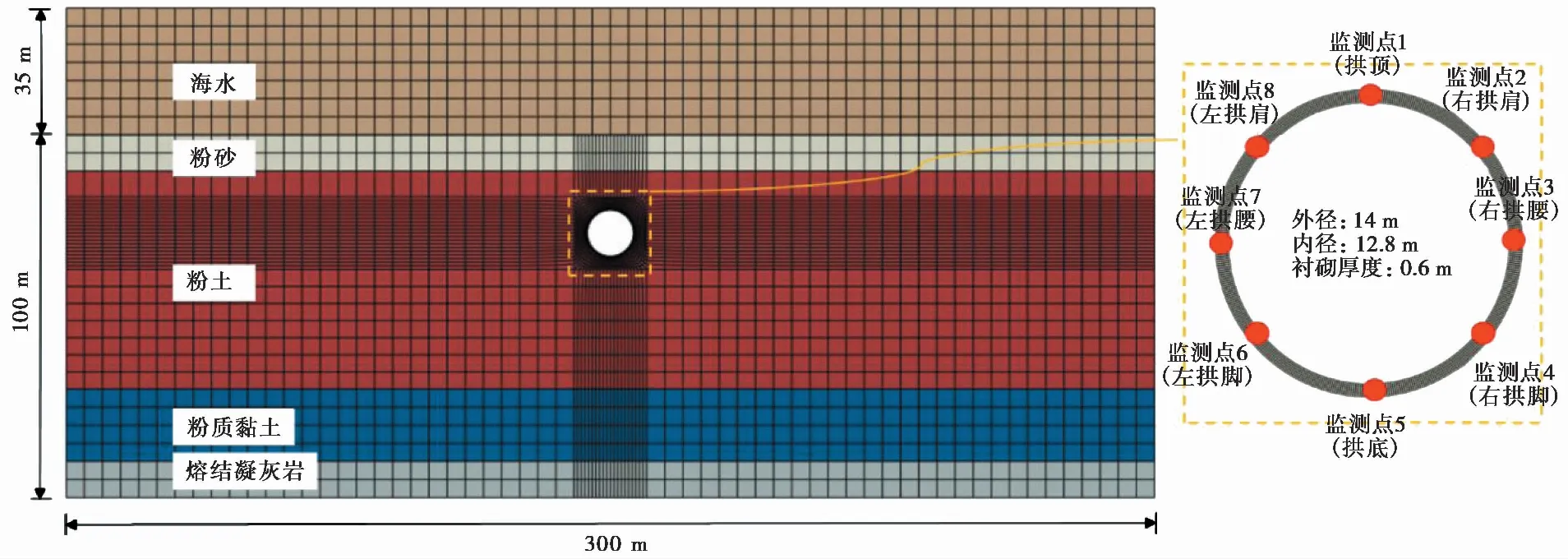
图 2 海水-海床-隧道耦合模型与隧道监测点分布示意图Fig. 2 Water-soil-tunnel coupling model and distribution of tunnel monitoring points

根据该工程场址的地震安全性评价结果，确定了小震、中震和大震的水平基岩峰值加速度分别取为0.03g， 0.075g和0.15g，其中，g为重力加速度。文中均采用0.15g(大震)地震动强度进行分析，在输入双向地震时将水平地震和竖向地震进行等比例调幅处理。在日本地震台网KIK-Net中分别选取MYGH03台站记录的发生于2013年的6级地震(简称MYGH03波)、MYGH04台站记录的发生于2009年的6.6级地震(以下简称MYGH04波)和发生于2008年的7.2级地震(简称MYGH04-2波)、FKS007台站记录的2016年的7.2级地震(简称FKS007波)作为基岩输入地震动。4条地震波相应的加速度时程和傅里叶频谱如图 3 所示(水平激励幅值0.15 g，竖向激励等比例调幅)，其中MYGH03波和MYGH04-2波记录的中高频成分较为丰富，而MYGH04波和FKS007波记录的低频成分比较丰富。

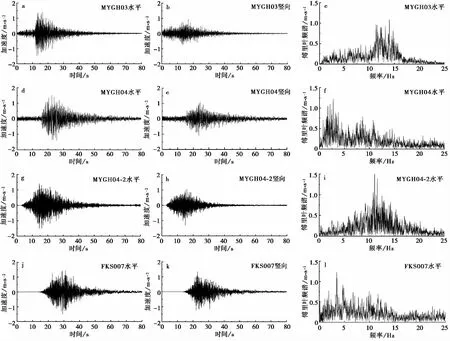
图 3 地震动的加速度时程及傅里叶谱Fig. 3 Acceleration time histories and Fourier spectra of the input bedrock motionsa. MYGH03水平加速度时程； b. MYGH03竖向加速度时程； c. MYGH03水平傅里叶谱； d. MYGH04水平加速度时程；e. MYGH04竖向加速度时程； f. MYGH04水平傅里叶谱； g. MYGH04-2水平加速度时程； h. MYGH04-2竖向加速度时程； i. MYGH04-2水平傅里叶谱； j. FKS007水平加速度时程； k. FKS007竖向加速度时程； l. FKS007水平傅里叶谱

3 计算结果及分析

3.1 地震动输入方向及频率分布影响

在埋深为20 m，水深为35 m的海水-海床-隧道整体模型底部基岩分别施加水平地震、水平+竖向双向地震。图 4和图 5 分别展示了隧道在单向和双向地震作用下各监测点处的应力峰值和整体塑性损伤分布云图(其中：损伤云图经过处理，为了便于展示扩大了其损伤范围，仅表征隧道损伤的位置及数量)。图 5损伤云图中的SEDG指的是混凝土刚度下降率，数值介于0(无损伤)到1(完全损伤)之间。从图 4 中可以看到在水平地震作用时隧道左右拱脚、拱肩处的应力峰值明显大于隧道拱顶、拱底和左右拱腰处。当处于双向地震作用时，隧道各监测点处的应力峰值明显增大。结合图 5 的混凝土塑性损伤云图，在双向地震作用时隧道出现了部分损伤，证明了隧道在双向地震作用下受到了更大损害。

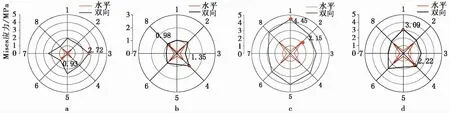
图 4 隧道各监测点峰值Mises应力Fig. 4 Maximum Mises stress of each monitoring point in tunnela. MYGH03输入; b. MYGH04-2输入; c. MYGH04输入; d. FKS007输入

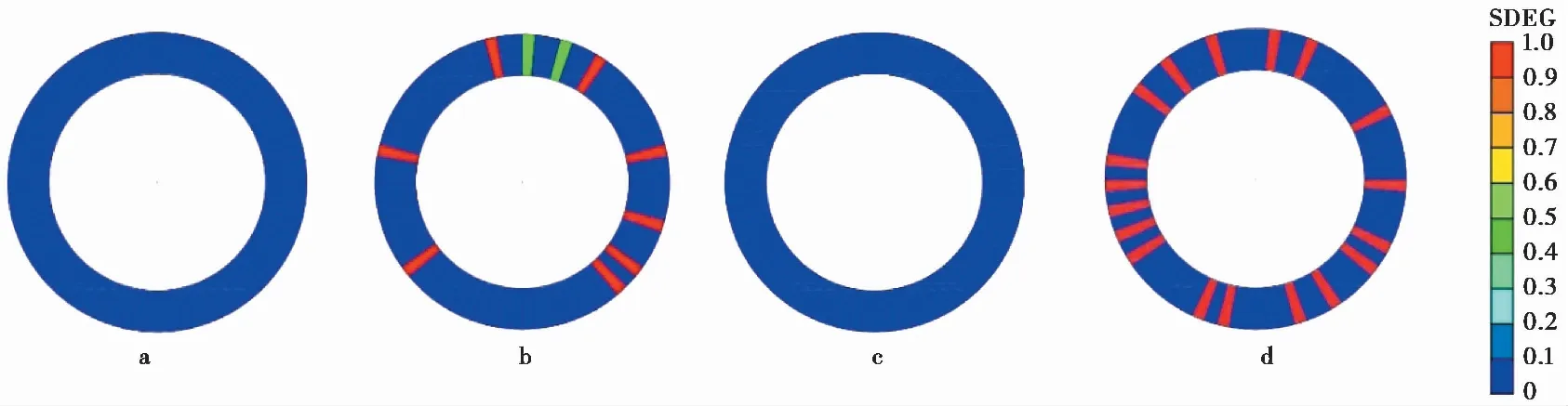
图 5 隧道损伤分布示意图(非原比例)Fig. 5 Distribution of tunnel damagea. MYGH03水平输入; b. MYGH03双向输入; c. MYGH04水平输入; d. MYGH04双向输入

由此可见，不同的地震动输入方向将显著影响海底隧道的地震响应特征。为了探究不同地震对动水压力的影响，图 6给出了不同地震动输入条件下的海床上覆海水最大动水压力分布云图。为便于展示，截取隧道左右两侧各50 m的水域的范围，图中标尺以隧道中心上方为0点左右延伸。如图 6a～图6h所示，地震作用下最大动水压力出现在隧道正上方两侧位置。相对无隧道自由海床(图 6i、图6j)而言，有隧道结构的海床上部(图 6a、图6e)最大动水压力明显增大。这是由于隧道-土体的相互作用导致隧道附近土体的局部竖向变形增大，从而在上覆海水中产生更明显的动水压力。在双向地震动输入时(图 6b、图6d、图6f、图6h)，海水整体动水压力明显增大，这说明动水压力的大小主要受竖向荷载影响。

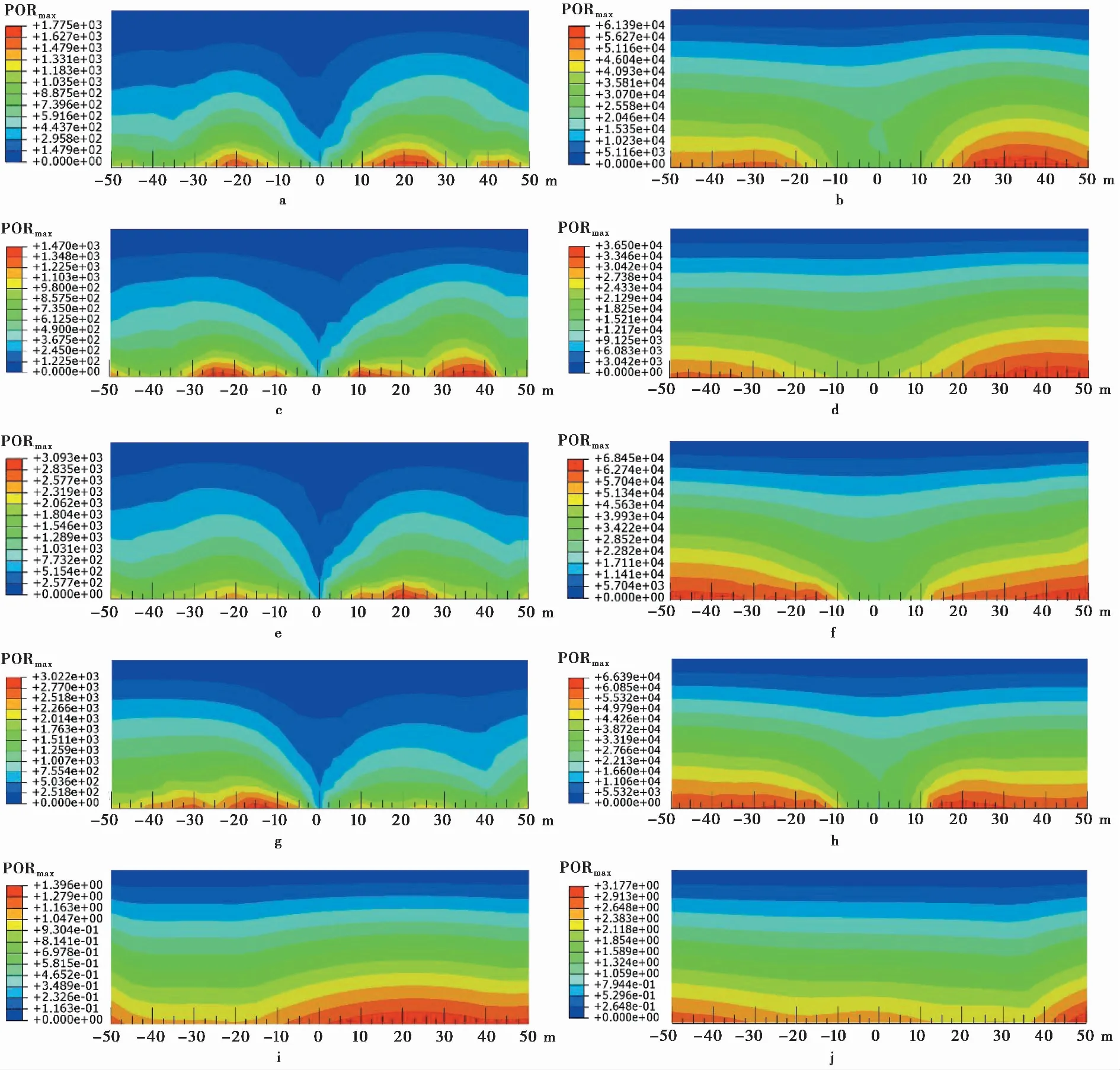
图 6 最大动水压力分布图(Pa)Fig. 6 Distribution of maximum hydrodynamic pressure(Pa)a. MYGH03水平输入； b. MYGH03双向输入； c. MYGH04-2水平输入； d. MYGH04-2双向输入； e. MYGH04水平输入； f. MYGH04双向输入； g. FKS007水平输入； h. FKS007双向输入； i. MYGH03水平输入(无隧道自由海床模型)； j. MYGH04水平输入(无隧道自由海床模型)

将中高频成分丰富的MYGH03波、MYGH04-2波与低频成分丰富的MYGH04波、FKS007波分别作为地震动输入，研究在不同类型地震作用下隧道的响应规律。从图 4 的峰值应力图中可以看到由于海域沉积土高频滤波、低频放大的特性，在水平向低频地震动输入时的隧道应力峰值对比水平向高频地震动输入时的隧道最大应力峰值明显增大，而在双向地震作用时也呈现出类似的规律。因此，在图 5 中双向高频地震动输入时，隧道出现了更显著的损伤分布。从图 6 中可以看到，由于海域沉积土低频放大高频滤波的特性，低频地震动输入下海床表面会产生更大的加速度，相同条件下其最大动水压力要大于低频地震动输入的模型，由此可见，地震动的频率分布会显著影响隧道的地震动力响应规律。

3.2 上覆水深影响

分别设置0 m、5 m、15 m、25 m、35 m 5种不同上覆海水深度，以此来分析其对于海底盾构隧道地震响应规律的影响。由上述分析可知在双向地震作用下的海底盾构隧道结构会产生较大的损伤，故分别提取了在两种不同的双向地震激励作用下的隧道受拉损伤云图，如图 7 所示。在不同地震激励及不同上覆水深条件下的隧道均出现了不同程度的受拉损伤，且隧道损伤多以裂缝形式出现。在低频分布丰富的MYGH04地震动输入下的隧道地震损伤面积明显大于相同水深下的MYGH03地震动输入下的隧道。此外，随着水深的增加，在两种不同的地震动输入情况下隧道受拉损伤云图均出现减小趋势，这可能是由于上覆海水对海床整体地震响应的抑制作用所致。可以看出，上覆海水的存在对海底盾构隧道在双向地震作用下的损伤规律有显著影响，建议在实际工程中，考虑水深变化对隧道地震安全性以及整体结构稳定性的不利影响，必要时加强局部隧道结构强度。

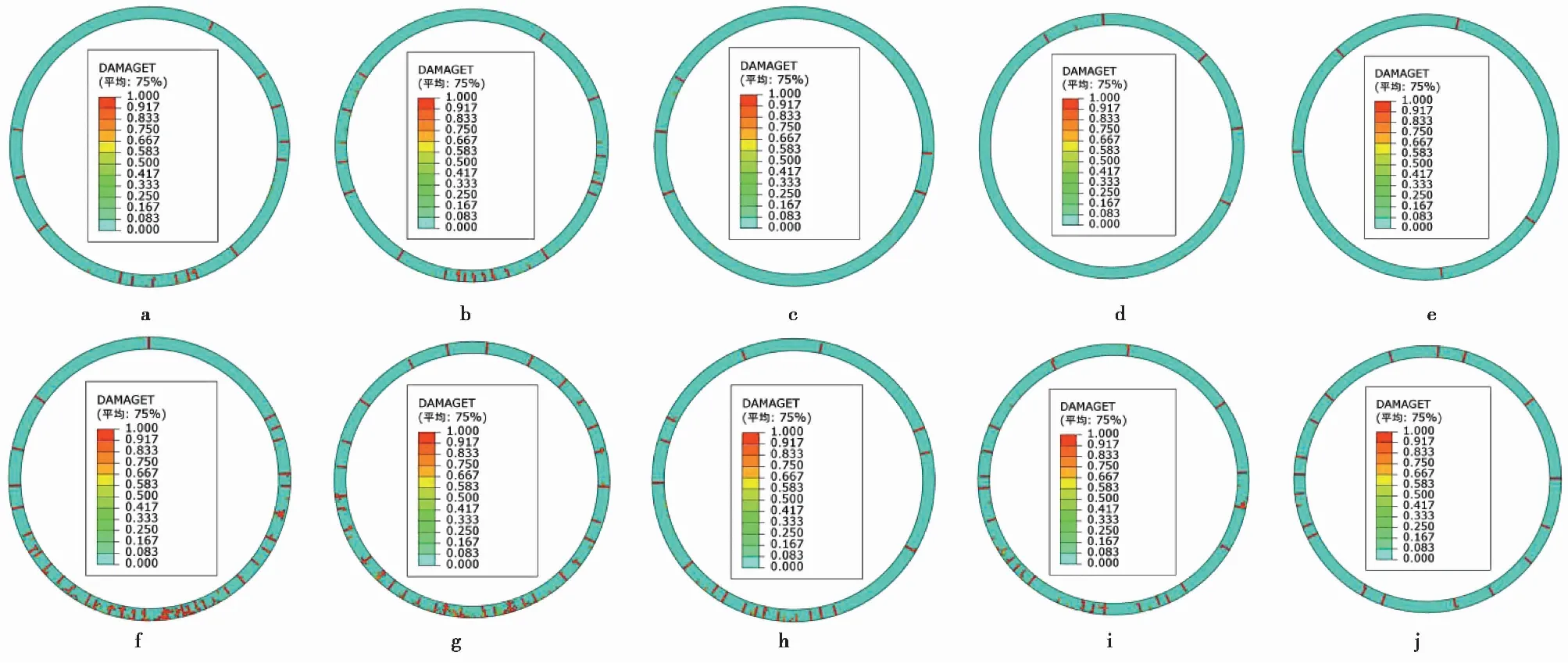
图 7 隧道结构的地震受拉损伤分布图Fig. 7 Seismic damages of tunnel at tension statea. MYGH03双向0 m; b. MYGH03双向5 m; c. MYGH03双向15 m; d. MYGH03双向25 m; e. MYGH03双向35 m; f. MYGH04双向0 m; g. MYGH04双向5 m; h. MYGH04双向15 m; i. MYGH04双向25 m; j. MYGH04双向35 m

图 8进一步给出了计算区域内最大动水压力随上覆水深的变化。可见，在不同地震动输入及不同地震激励方向作用下，最大动水压力均随着水深的增加而不断增加。并且，在水平地震作用下的最大动水压力较小且不同水深下数值相差不明显，而在双向地震激励下，最大动水压力远大于水平地震作用下的动水压力，且随着水深增加而增加的趋势更加显著。

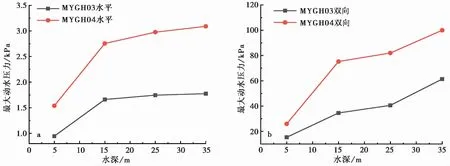
图 8 计算区域内最大动水压力随上覆水深度的变化Fig. 8 Variation of maximum hydrodynamic pressure with water depth in the calculation domaina. 水平地震下最大动水压力变化; b. 双向地震下最大动水压力变化

4 结 论

本文采用声-固耦合的方法建立了海水-海床-隧道整体耦合的有限元分析模型，探讨了在不同地震激励及覆水深度条件下海底隧道的非线性地震响应规律，主要结论如下：

(1)通过与解析解的对比，验证了ABAQUS中采用声学模块进行流-固耦合模拟能够准确地计算水域内的动水压力。

(2)当仅在水平地震激励作用下时，海底盾构隧道最大应力主要集中在隧道左右拱肩及拱脚处； 海域最大动水压力出现在隧道正上方两侧海床表面处。当处于双向地震激励时，海床表面动水压力显著增大，隧道各点处的应力峰值也随之增大，表明海底双向地震激励对海底隧道更加不利。

(3)由于海域软土场地在受到海底地震作用时具有低频放大、高频滤波的特性，相较于高频丰富的地震动激励，低频丰富的地震动激励对于海底隧道的危害更大。

(4)上覆水深变化对海底隧道的地震反应有较大影响； 上覆水深越深，双向地震激励下的海底隧道结构损伤越小，水深对于海底隧道的动力响应影响比较复杂，后续我们将针对水深较大时展开更加深入的研究。