W型封头冲压成型过程的数值模拟及参数优化
2022-01-22李鸿超
李鸿超
(斯派莎克工程(中国)有限公司,上海 201400)
0 引言
结晶罐采用W型封头能改善溶液混和的均匀性,避免局部产生过高的溶质饱和度,能得到较好的结晶效果[1]。W型封头的加工一般采用冲压成型方法,在上下模腔的约束下对金属板料施加压力,使之产生塑性变形[2]。材料性能、模具尺寸、润滑条件、加载速度等因素都会对成型性能产生影响[3],如产生起皱[4]、拉裂、回弹等成型缺陷[5-6]会严重影响冲压件的几何精度、力学性能和表面质量。冲压成型过程是一个同时包含几何、材料、边界条件非线性,并涉及大位移和大变形的力学问题,很难通过常规的数学、力学方法深入了解过程中材料塑性流动和塑性强化、应力应变、接触摩擦的规律[7]。传统的试验法、经典理论分析法[8]对金属成型过程的研究多停留在定性和经验统计分析阶段,很难确定各因素的影响,因而不能很好地预测和控制成型过程。有限元法的发展能较好地克服传统研究方法的缺陷,通过数值模拟技术可以综合分析冲压成型过程中的各因素对成型的影响。国内已经对板料冲压成型的有限元仿真开展了一些基础的应用研究[9-11],但在冲压模具的优化设计和冲压工艺制定方面的研究较少,更鲜有文献对W型封头的成型过程及成型规律进行研究。
本文采用ABAQUS软件建立了W型封头冲压成型过程的有限元模型,对影响成型性能的关键参数进行了分析研究,并基于优化的参数方案进行了成型过程的模拟和分析,验证了W型封头冲压成型的数值仿真方法,以期为W型封头的工艺选择及应用提供支撑。
1 W型封头冲压成型有限元模型(数值仿真)
1.1 网格模型及边界条件
本文建立的有限元模型包括标准椭圆封头、冲模及凹模,主要的几何参数为:封头直径为1200 mm,封头厚度为4 mm,封头高度为300 mm;冲模为半球形冲头结构,冲头半径R为200 mm;凹模的圆弧半径R1、R2分别为150 mm、200 mm。封头采用壳单元S4R进行网格划分,共1805个单元。冲压时冲模及凹模的变形较少,仿真分析时直接将其设为刚体,采用刚性单元R3D4进行网格划分,冲模、凹模的单元数分别为880和1365。划分网格后的模型及模型的几何尺寸如图1所示。
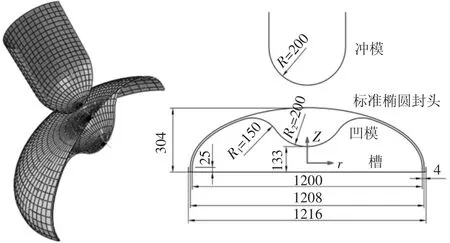
图1 网格模型及主要几何尺寸
为提高计算效率,建立了1/2轴对称模型,在模型的对称面上约束周向自由度。整个仿真过程中,约束凹模的所有自由度。设置冲模的运动速度,其运动过程包含两部分:1)向下的冲击运动,此时约束椭圆封头底边的所有自由度;2)冲击后的向上归位运动,此时卸除封头的所有约束条件。
1.2 材料及接触模型
标准椭圆封头的材料为06Cr19Ni10,材料的基本参数为:密度[12]ρ=7930 kg/m3,泊松比μ=0.3,弹性模量E=206 GPa。当涉及大位移和大变形时,材料的非线性本构关系对数值模拟的准确性具有关键影响。本文采用弹塑性材料模型对W型封头的冲压过程进行模拟,该模型可预测成型后的材料回弹及残余应力,本构方程[13]为

冲压过程中,封头与冲模、凹模之间均有接触运动作用,需设置合理的接触类型及参数,保证接触界面之间不发生穿透,同时考虑摩擦作用对接触界面相对运动的影响。本文采用surface-to-surface接触类型,椭圆封头的表面定义为目标面,凸模、凹模、压边圈和压件板的表面均定义为接触面。接触方法采用罚函数法,考虑到摩擦效应,设定初始的摩擦因数为0.1。
2 W型封头成型仿真的参数影响分析
影响W封头冲压成型性能的关键因素包括材料力学性能参数、冲压工艺参数等。封头材料确定后,通过调整冲压过程中的摩擦因数、冲压速度、冲压深度及模具的几何参数等,可获得既能满足设计要求又能避免产生成型缺陷的最优方案。
通过仿真模拟提取并对比W型封头冲压过程中的最大主应力、等效塑性应变、最小厚度及冲模的回弹量等数据,分析各参数变化对成型性能的影响。冲模在圆周方向共39个节点,假设其变形前后各节点的r坐标保持不变,则其回弹量可按照下式进行计算:
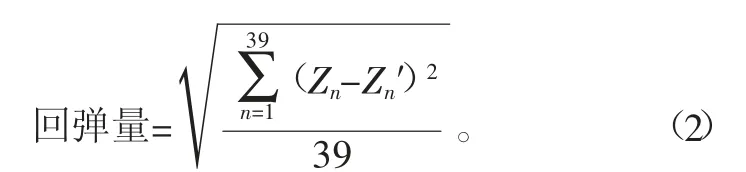
式中:n为节点数;Zn为回弹后各节点的z向坐标;Zn′为回弹前的z向坐标。
2.1 摩擦因数的影响
W型封头的冲压成型仿真时,冲模与工件、工件与凹模之间均有接触,为简化分析,对2组接触对设置相同的摩擦因数,分别为0.10、0.15、0.20、0.25,结果如表1所示。由表1可知,摩擦因数为0.20、0.25时,最大主应力、等效塑性应变、回弹量较小,而最小厚度值较大,成型状态较好。考虑到工程实际需要,选择0.2为最优摩擦因数。

表1 不同摩擦因数对成型性能的影响
2.2 冲压速度的影响
冲压仿真时设置相同的冲模运动行程,通过修改冲模运动的时间实现对冲压速度的控制。冲压的行程距离设置为288 mm,冲压时间分别取为0.005、0.008、0.010、0.030、0.050、0.100 s进行模拟,结果如表2所示。由表2可知,随着冲压速度的减小,最大主应力降低,等效塑性应变减小,说明在冲压过程中封头发生拉裂的可能性降低;冲压速度下降后,最小厚度减小,回弹量先减小后增大,转折点为冲压时间0.05 s的工况。0.10 s和0.05 s冲压时间工况下的最大主应力、等效塑性应变、最小厚度相差无几,但后者的回弹量更小,成型形状更佳,因此选定冲压时间0.05 s时对应的冲压速度5.76 m/s作为最优参数。
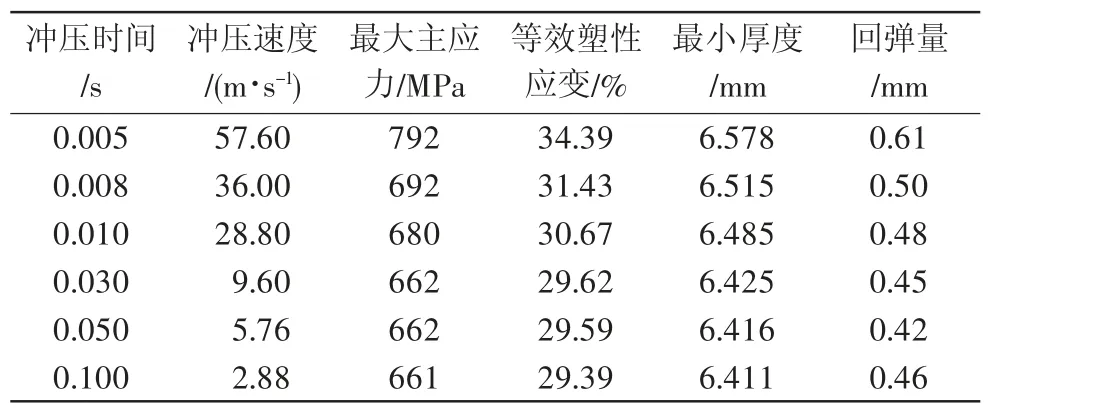
表2 不同冲压速度对成型性能的影响
2.3 冲压深度的影响
结合工艺要求,分别取冲压深度为148、168、188、208 mm进行对比分析。为节省模拟计算时间,冲压时间统一设定为0.01 s,模拟结果如表3所示。由表3可知,随着冲压深度的增加,最大主应力和等效塑性应变均增大,冲压时更容易发生断裂;与此同时,最小厚度减小说明冲压后厚度变薄的趋势增大。因此确定最优的冲压深度为148 mm。
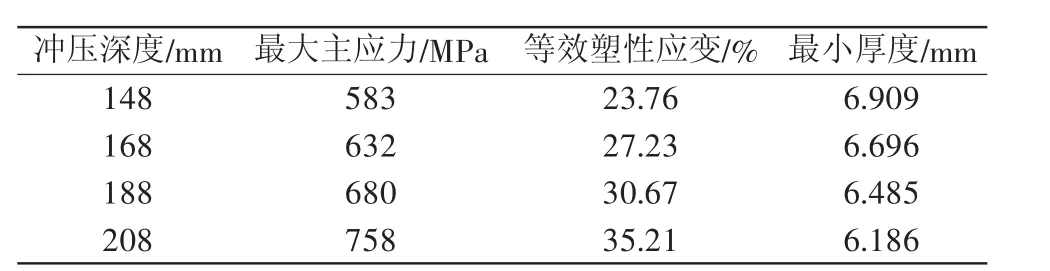
表3 不同冲压深度对成型性能的影响
2.4 凹模圆弧半径的影响
对W型封头冲压使用凹模的两段圆弧半径尺寸的影响进行分析。首先取圆弧半径R1分别为125、150、175、200 mm进行模拟优化,冲压时间统一设定为0.01 s,模拟结果如表4所示。随着圆弧半径R1的增加,凹模的起伏趋于平缓,最大主应力和等效塑性应变均呈现减小的趋势,对封头成型后的整体状态有利;最小厚度逐渐增大,与工程需要的厚度值更接近。因此,建议凹模圆弧半径R1取为200 mm。

表4 凹模圆弧半径R1对成型性能的影响
随后对圆弧半径R2的影响进行分析,R2分别取值为175、200、225、250 mm,冲压时间统一设定为0.05 s,模拟结果如表5所示。由表5可知,当圆弧半径R2为225 mm时,最大主应力和等效塑性应变均最小,最小厚度值虽不是最优,但与R2为250 mm时的最小厚度相差不大。此时的回弹量为0.39 mm,也符合要求。因此R2最优值取225 mm。
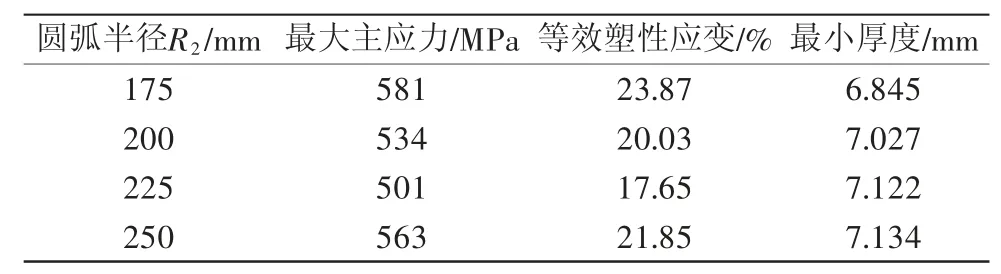
表5 凹模圆弧半径R2对成型性能的影响
3 仿真优化结果及分析
基于以上对W型封头成型仿真参数的影响分析,获得的优化方案为:摩擦因数为0.2,冲压速度为5.76 m/s,冲压深度为148 mm,凹模圆弧半径R1为200 mm,凹模圆弧半径R2为225 mm。基于优化参数对W型封头的冲压成型过程进行仿真,成型过程如图2所示。
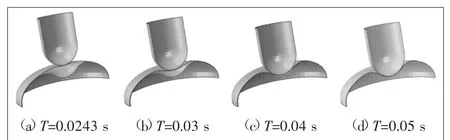
图2 W封头冲压成型的过程
提取封头在图2对应4个时刻的最大主应力云图(如图3),并对成型过程中的最大主应力、等效塑性应变、厚度数据沿半径方向的变化(如图4)进行分析。

图3 最大主应力变化云图
1)T=0.0243 s时。冲模与椭圆封头刚好接触,在冲模的推动下封头与凹模开始接触成型。封头中心区域的最大主应力较大,沿半径方向呈逐渐减小的趋势,边缘处最小;板料开始发生不均匀的塑性变形,与冲模的接触面处变形较大;冲模的冲压作用导致封头中心区域的厚度略有减小,凹模的挤压作用导致封头与凹模接触的边缘位置厚度略有增大,其他部位厚度基本保持不变。
2)T=0.03 s时。冲模逐渐向下冲压,与封头的接触区域扩大,第一阶段成型结束;最大主应力、等效塑性应变、厚度的分布趋势和T=0.0243 s时大致相同,封头中心的大应力区域、发生塑性变形的区域均扩大,中心位置的厚度变小。
3)T=0.04 s时。冲模与封头、封头与凹模之间的接触区域继续增大,板料在接触区域开始发生大的塑性变形;最大主应力的最大值由封头中心慢慢向以R1为半径的圆弧和以R2为半径的圆弧的相切处转移;板料厚度变化不均匀,接触区域的厚度明显减小。
4)T=0.05 s时。冲压成型结束,封头外缘的最大主应力值较小,中间部位明显增大,最大值位于以R1为半径的圆弧和以R2为半径的圆弧相切处;封头经历大变形后,仍有部分区域处于弹性变形阶段,应变的最大值也发生在R1和R2的圆弧相切处;封头与冲模接触部位的厚度明显减小,最薄处同样位于R1和R2的圆弧相切处。
4 结论
本文采用ABAQUS有限元分析软件建立了W型封头冲压成型的有限元模型,基于模型对冲压成型过程进行了数值模拟,并对影响成型性能的参数进行了优化分析。主要结论如下:1)对摩擦因数、冲压速度、冲压深度及凹模尺寸的影响进行了敏感性分析,得到了最优的参数方案:摩擦因数为0.2,冲压速度为5.76 m/s,冲压深度为148 mm,凹模的2个圆弧半径分别为200 mm、225 mm;2)对最优参数方案时的冲压过程进行了仿真分析,最大主应力、等效塑性应变及封头厚度的变化趋势显示,冲压过程中最容易发生断裂的位置为以R1为半径的圆弧和以R2为半径的圆弧相切处。
