不规则图斑椭球面积计算的数值积分方法
2022-01-21王建伟李思卓樊康尧
赵 辉 王建伟 李思卓 樊康尧
(1.自然资源部大地测量数据处理中心, 陕西 西安 710054; 2.自然资源部第二地形测量队, 陕西 西安 710054)
0 引言
面积计算是国土调查的一项重要工作,对于不规则图斑的平面面积计算已有简单易行的公式,但高斯-克吕格投影是等角横切椭圆柱投影,存在面积变形,离中央经线越远变形越大,而椭球面积可避免此问题。已有许多学者对平面面积和椭球面积及不同坐标系的变化做出深入研究[1],王解先等[2]讨论了高斯投影中央子午线变化和投影面高程变化引起的面积变形,分析了椭球面积和平面面积的差异;党亚民等[3]研究了不同坐标系坐标转换对国土资源调查面积量算的影响;杨润书等[4]计算了高原地区不同坐标系及投影面引起的面积误差。
地球椭球面是一个曲面,椭球面积的计算相对复杂。在计算由子午圈和平行圈围成的椭球面梯形时,对微分面积进行积分,并将被积函数展开级数分项求积后再相加[5];施一民等[6]利用测地坐标推导了椭球面上测地格网曲边矩形的面积;林绿等[7]将椭球面上区域投影到赤道平面,利用二重积分的方式计算曲面面积。对于不规则图斑,第三次全国国土调查技术规程中在多边形边上内插一定的加密点,将任意封闭区域分割成有限个梯形图块,求出各小梯形图块后累加得到总面积[8];史守正等[9]改进了图斑面积的定积分近似计算方法,简化了椭球面积的计算过程。也可以通过求取平面面积和椭球面积的转换关系,将平面面积转换为椭球面积。刘洋等[10]顾及地球曲率,对高斯投影面积变形进行抛物线拟合,然后修正高斯投影面积;茹仕高等[11]从高斯投影面积变形原理出发,引入格网改正法建立了高斯投影面积与椭球面积的修正系数。
本文从椭球面积计算严密公式出发,对大地坐标形式的不规则图斑直接采用数值积分方法计算椭球面积,并通过算例分析验证方法的可行性与精度。
1 椭球面积计算方法
1.1 椭球面梯形图幅面积
由两条子午线和两条平行圈围成的椭球面梯形,微分面积dP等于子午线微分弧长dx和平行圈微分弧长dy的乘积:
dx=MdBdy=NcosBdL
(1)
则
(2)
求积后得
(3)
由于公式(3)计算复杂,对式(2)中被积函数进行级数展开,再分项积分得:
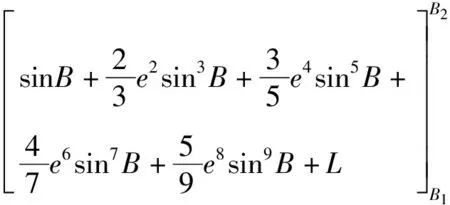
(4)
1.2 任意图斑椭球面积计算的传统方法
本文将文献[8]的任意图斑椭球面积计算称为传统方法,对于不规则多边形图斑可以分割成有限个梯形图块,对每个梯形图块进行叠加得到总面积。如图1所示,主要思路为:指定一条经线L0,将多边形P1P2边的两端点投影到经线L0上,得到P′1P′2,围成梯形图块P′1P′2P2P1,然后对P1P2边插入一些加密点Pi,沿纬线再将梯形图块分割为多个小梯形图块P′iP′i+1Pi+1Pi,分隔到一定程度,小梯形面积可根据公式(4)进行计算,累加小梯形面积得到梯形图块P′1P′2P2P1的面积,累加所有多边形边的梯形图块面积得到多边形图斑面积。
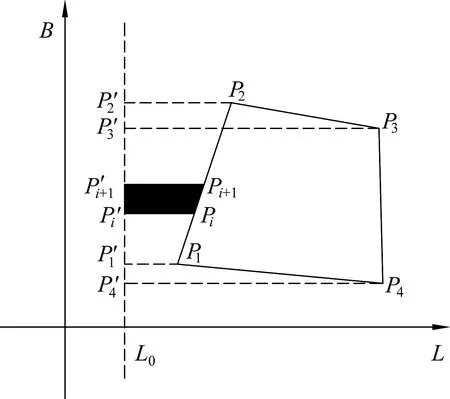
图1 传统方法任意图斑椭球面积计算
2 数值积分椭球面积计算方法
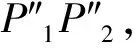
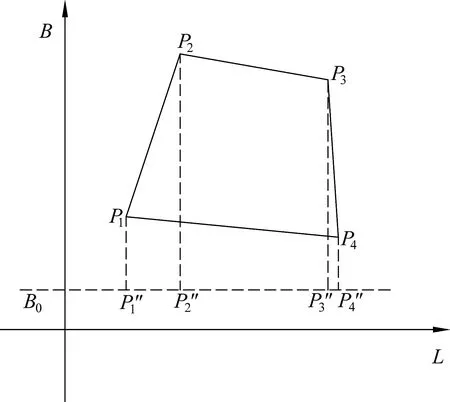
图2 数值积分方法任意图斑椭球面积计算
(5)
B的积分下限为B0,积分上限P1P2为大地线,根据大地线微分方程,可建立大地线上经纬度的关系
B=u(L,BP1,LP1,BP2,LP2)
(6)
对B积分
(7)
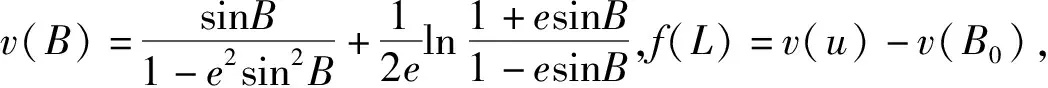
(8)
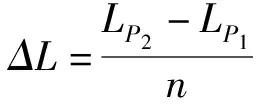
(1)矩形法:
(9)
(2)梯形法:
(10)
(3)Simpson法:
(11)
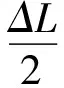
3 算例分析
以1∶10 000标准分幅大小进行实验分析,选取I49G024001图幅,四角点坐标见表1。参数使用2000国家大地坐标系椭球参数,长半轴a=6 378 137 m,扁率f=1/298.257 222 101。

表1 标准分幅I49G024001四角点大地坐标
如表2所示,根据公式(3)严密公式计算的椭球面积为26 367 263.059 3 m2,根据公式(4)计算的椭球面积同样为26 367 263.059 3 m2,再利用公式(9)~(11)验证数值积分方法的正确性。由公式(3)可知,椭球面积与纬度、经差有关,而与经度无关,因此,对于经线纬线围成的标准分幅图斑不需要划分子区间,1个区间即可直接计算。

表2 数值积分方法计算的梯形图斑椭球面积 单位:m2
为了模拟任意不规则图斑,选择表1中ABC、ACD构成两个三角形。这时已经不能用严密公式计算其准确的椭球面积,采用1.2中传统方法和本文提出的数值积分方法计算,进行比较分析。
在区间划分方面,采用二分的方式,第二次划分是前一次的2倍,加快迭代过程。表3~6限于篇幅,ABC和ACD显示面积减去了13 180 000 m2,两个三角形的面积和减去了26 360 000 m2。
表3列出了传统方法计算的三角形结果,可以看出当划分1个区间时,计算的两个三角形面积相等,ABC补的面积大于割的面积,ACD补的面积小于割的面积,最终面积都等于沿纬线中点对ABCD图斑切割后的分割图块面积。随着划分个数的增加,ABC和ACD面积都逐渐趋于稳定,但受变量的数值精度影响,两个三角形的面积和发生变化。
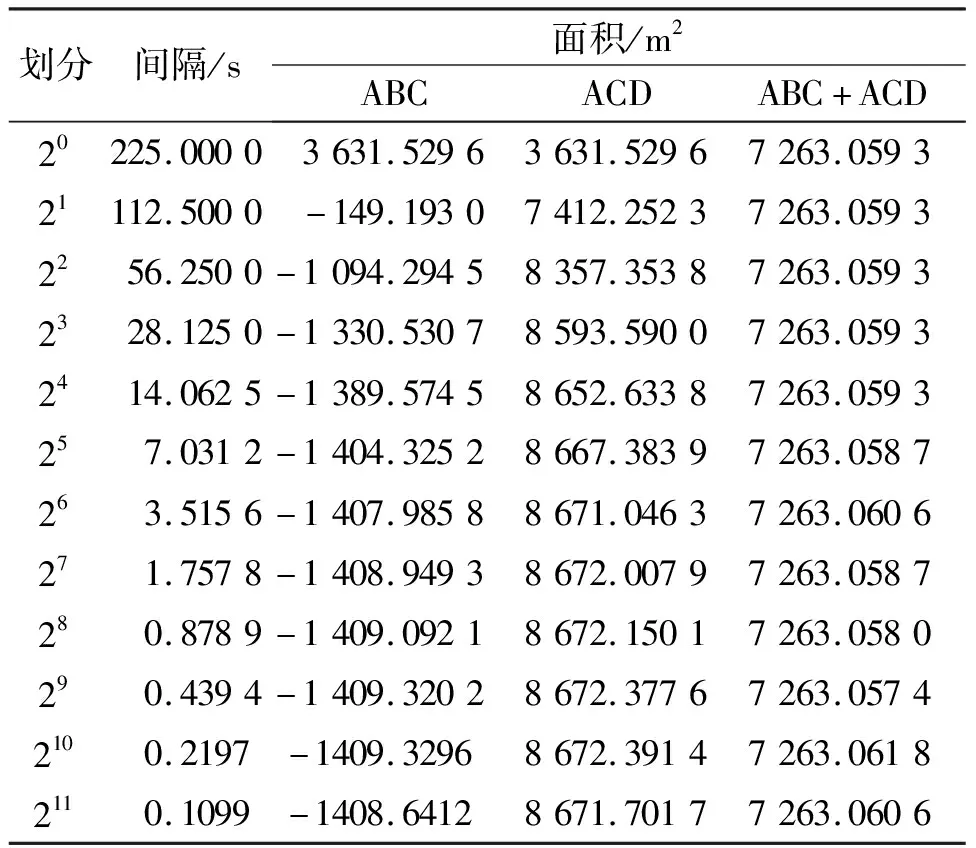
表3 传统方法计算的不规则图斑椭球面积
表4~6列出了三种数值积分方法的计算结果显示,相对于传统方法,数值积分方法的面积和较为稳定。矩形法和梯形法计算结果接近,划分210个区间面积变化小于0.01 m2,而Simpson法表现出了优越性,划分24个区间面积变化小于0.01 m2,划分28个区间面积变化小于0.001 m2,划分210个区间面积变化小于0.000 1 m2。

表4 矩形法数值积分计算的不规则图斑椭球面积
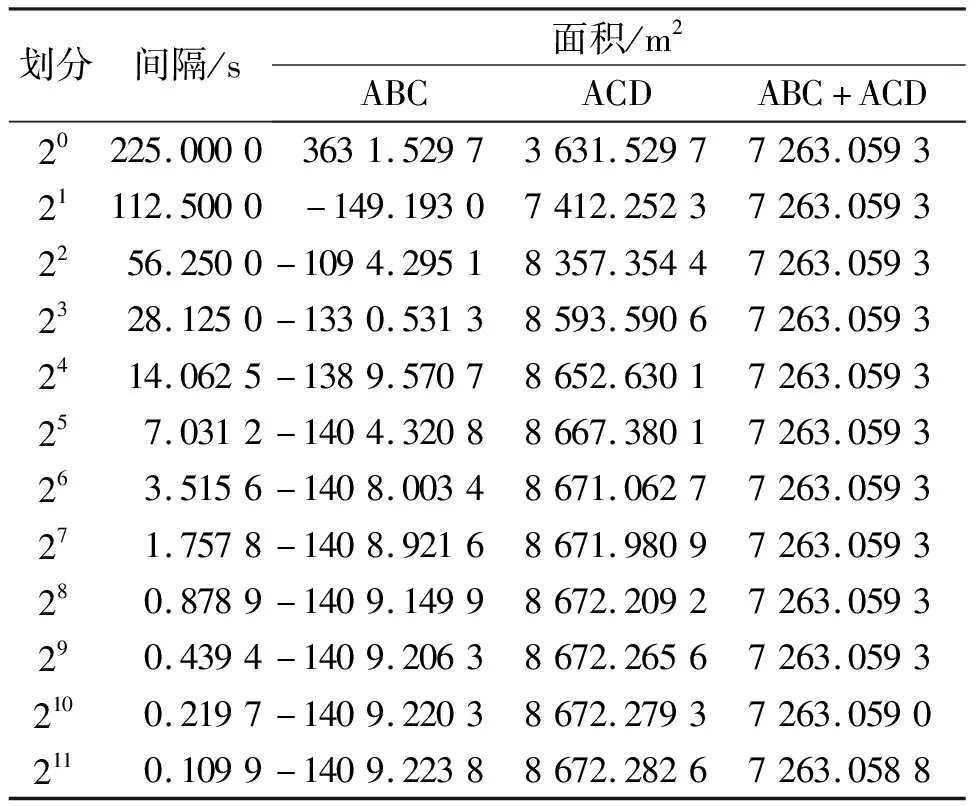
表5 梯形法数值积分计算的不规则图斑椭球面积
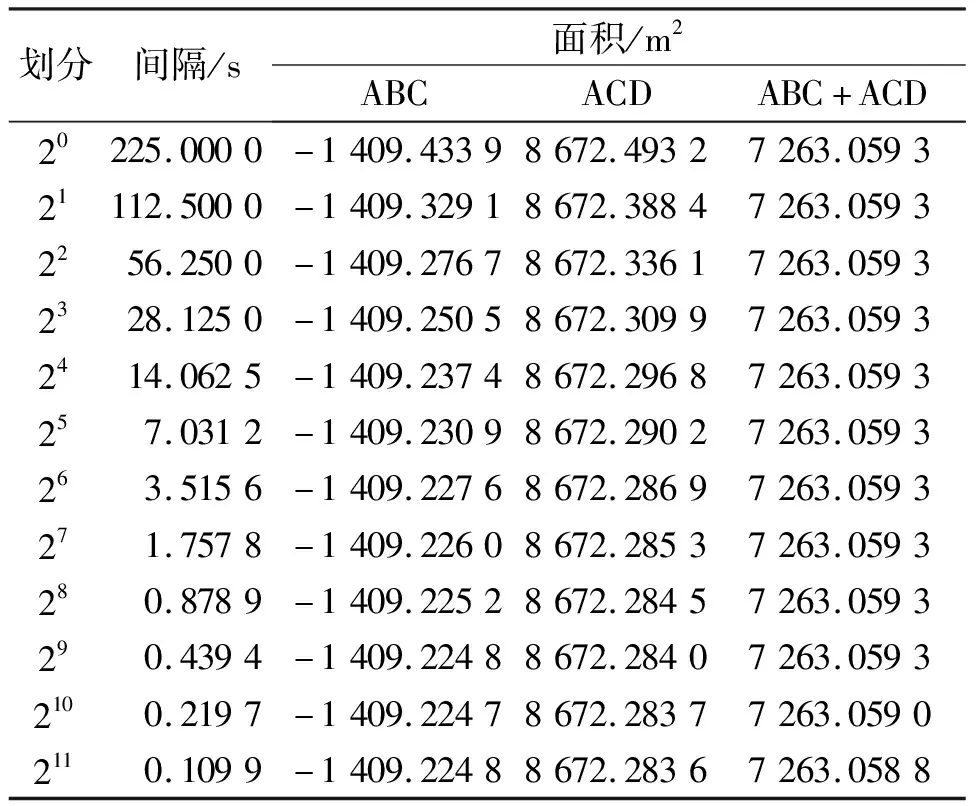
表6 Simpson法数值积分计算的不规则图斑椭球面积
同时,结果也显示分割的两个三角形ACD比ABC椭球面积大10 081.51 m2,传统方法按一个区间计算,则ABC面积多补了5 040.75 m2,ACD面积多割了5 040.75 m2。
4 结束语
针对不规则图斑的椭球面积计算,传统方法是在不规则图斑的边界上插入加密点,构造近似椭球面梯形图块,按规则梯形椭球面积计算公式求解后累积求和得到总面积。本文提出了基于数值积分思想的不规则图斑椭球面积计算方法,利用实验数据进行比较分析,得出以下结论:
(1)传统方法为了提高计算精度需要插入一定密度的加密点,随着密度的增加,受数值精度影响变大,而数值积分方法影响较小;
(2)数值积分方法中Simpson法比矩形法和梯形法效率更高,能够快速求出不规则图斑的椭球面积,且精度可靠。
