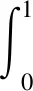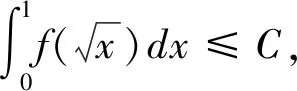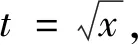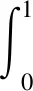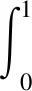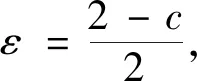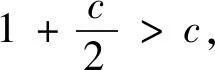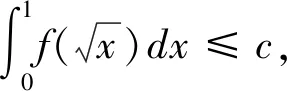最佳常数问题的几类证法研究
2022-01-21廖春艳
廖春艳,罗 凤
(湖南科技学院 理学院,湖南 永州 425199)
有关最佳常数问题的证明对证明技巧和综合运用知识能力要求较高,证明方法灵活多变。文献[1-2]对历年来考研竞赛试题中出现的积分等式及不等式的证明方法做了专题介绍。文献[3]主要是对包含f(x),f′(x),f″(x)的积分不等式的最佳常数进行了深入分析,因为对区间的分割不断改进,得到了更加精细的计算结果,最终得到了最佳的积分常数。文献[4]是在文献[3]的基础上给出了利用二等分法证明了包含f(x),f′(x),f″(x)的积分不等式,并证明了这个最佳常数为p=4。在上述文献中,更多的是集中在对积分不等式证明方法的讨论,而对不等式中的关键常数研究并不多[5-6],本研究将给出几种证明最佳常数的常用方法。
1 利用著名积分不等式证明最佳常数问题
引理2.1[1](Schwarz积分不等式引理)设f(x)和g(x)在[a,b]上可积,则有Schwarz不等式:
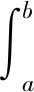
若f(x),g(x)∈C[a,b],则当等号成立时,当且仅当存在不同时为0的常数α,β,使得αf(x)=βg(x)。
引理2.2[1](Chebyshev不等式)若函数f(x),g(x)在[a,b]上连续,且f(x),g(x)在[a,b]上单调性一致,则有:
Schwarz积分不等式和Chebyshev不等式在很多重要场合都可以用到,在考研竞赛试题中也有广泛应用。在积分不等式中,如果被积函数或积分出现了平方形式,可以考虑利用Schwarz积分不等式进行证明。在解决区间上含有单调并且连续的被积函数的积分不等式这一类问题时,可使用Chebyshev不等式去证明。证明中巧妙利用一些著名积分不等式是处理积分不等式的重要方法与技巧。
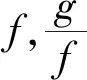
并说明右边系数2是最佳的。
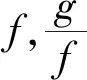
证明由Chebyshev不等式可得:
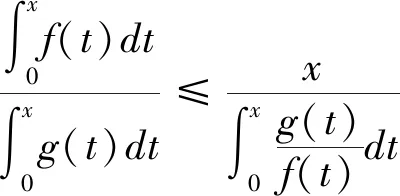
由Schwarz积分不等式得:
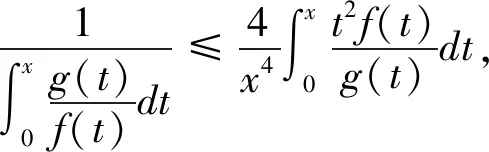
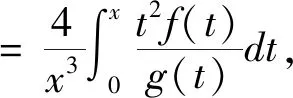
以下证明积分不等式中的2为最佳常数,令
f(t)=1,g(t)=t+ε,ε>0,则:
=2ln(1+2ε)-2ln2-2lnε,
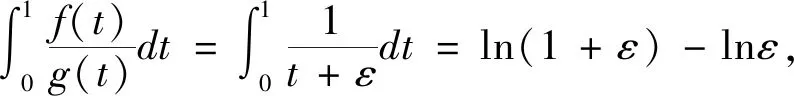
故由此可得2为此积分不等式中的最佳常数。
2 利用Lagrange中值定理证明最佳常数问题
Lagrange中值定理在数学分析中的微分学中占据核心地位,它是联系函数与导数之间的桥梁,也是微分学应用中的一个桥梁,在理论研究领域和实际中都有着很高的价值。在证明积分等式及不等式中,如果含有f(x)及导数f′(x),f″(x)或含有最值时,最常用的方法是借助微分中值定理进行分析,在解决过程中往往需要依据所要证明的不等式来构造辅助函数。
例2 设函数f(x)在[0,1]上二阶连续可导,则:
且右边的常数4不能用更小的数值代替。
分析:函数f(x)在闭区间[0,1]上二阶连续可导,闭区间上的连续函数满足最值性、介值性,同时由条件易知满足了微分中值定理的条件,因此在证明过程中试图从最值性和中值定理这两个角度出发来证明,同时发现在积分不等式中被积函数都带有绝对值,由此想到可以借助积分的绝对值性质来证明。
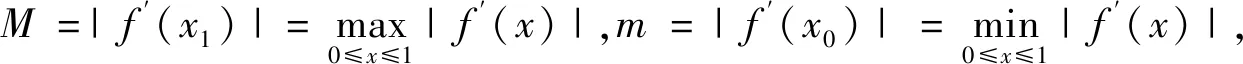
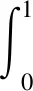
=|f′(x1)-f′(x0)|≥|f′(x1)|-|f′(x0)|
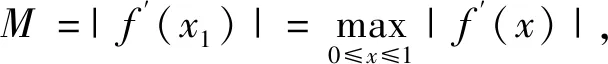
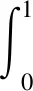
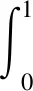
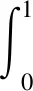
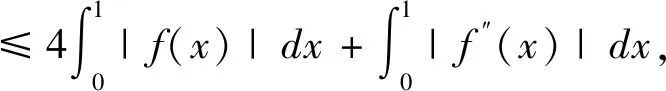
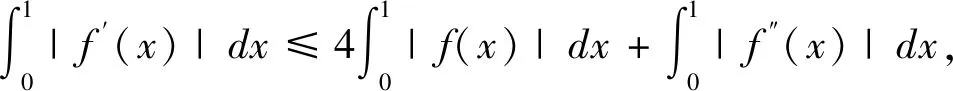
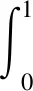
②若f(x)在[0,1]上没有零点,那么不妨假设f′(x)>0,即f(x)在[0,1]上严格单调递增。
(i)当f(x)≥0,x∈[0,1]时,由Lagrange中值定理可知:
f(x)-f(0)=f′(ξ)x,则:
(ii)当f(x)≤0,x∈[0,1]时,
(iii)当f(x)在区间[0,1]上有唯一零点时,记该点为a,可得:
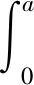
以下证明常数4不能用更小的数值代替,若假设0 由以上的代入结果可以得出的结论为k≥4,这与假设0 积分不等式的证明在数学中是最常见的题型,通过构造函数列来解决问题时,通过观察题目的条件和结论,设法构造一个符合题目条件的函数列,先找到基于该特殊函数列的常数,再证明该常数是最佳常数。这类型题目最难的是构造合适的函数列,这种方法从特殊情况出发,既可以简化证明,又能培养学生创新性。 分析:此题目要证明的是实数C最小值为c=2,是一个最值问题,也就是一个最优解问题,可以用构造函数列来解决最优解问题。通过构造函数列,利用积分进行求解,构造函数列最好构造熟悉简单的函数列,有利于求解。 fn(x)=(n+1)xn,x∈[0,1] 由于被积函数在积分区间上为非负,因此 因此在满足条件的函数列{fn(x)}下,c=2。 由不等式的左边可得: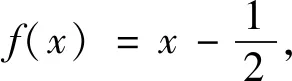
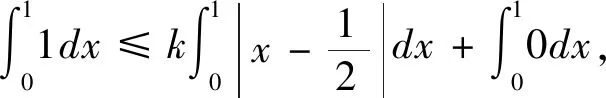
3 构造函数列证明最佳常数问题