ABAQUS技术在地下管道动力分析中的应用

国 艳，张文静，肖 遥，李林侗

(辽宁省地震局，沈阳 110034)

地下工程的快速发展给人们带来了便利，但其抗震安全性也越发重要。地下结构建设花费高，修复难，一旦破坏，将会产生巨大的经济损失与社会影响。相关研究指出[1]，由于管道自身重量较小，管道周围土体对其约束较大，其应力主要由周围土体的相对位移引起，在分析地下管道时，对于横截面积不大的直管，弯曲应力较小，可仅考虑轴向应变。在进行地下结构抗震性能分析时，可利用ABAQUS有限元分析软件。对计算结果的准确性和收敛性起关键作用的因素包括荷载与边界条件、相互作用、分析方法等。

为简化分析模型，假设土体为各项同性，静力分析时仅考虑自重和固定人工边界，动力分析时改变荷载和边界，采用黏弹性边界和地震荷载，在土体与结构间相互作用时采用接触面法来进行模拟。

1 常用人工边界

应用数值方法研究地震波在介质中的传播，考虑土-地下结构动力相互作用(SSI)，许多学者提出多种人工边界理论。进行数值模拟时，人工边界方法非常多，包括静力人工边界、动力人工边界、固定边界、滚轴边界、黏性人工边界、黏弹性人工边界、一致边界、旁轴边界、透射边界、自由边界、刚性边界、吸收边界、显式人工边界、整体人工边界、局部人工边界、离散人工边界、隐式人工边界等。

1.1 黏性人工边界

黏性人工边界理论最早是1969年John Lyrsmer[2]提出来的，主要是研究无限域的动力分析数值方法，适用于瞬态和稳态问题。将无限域替换为有限域，该区域受边界条件的约束，边界条件可模拟能量吸收边界。通过有限元法进行分析，在人工边界设置阻尼器用以吸收能量，解决应用于地基振动问题。黏性人工边界条件可以表示为：

(1)

(2)

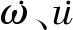
1.2 黏弹性人工边界

黏弹性人工边界理论是1994年Deeks[3]提出来的，采用的推导过程与黏性边界类似，实质是在人工边界上布置具有一定阻尼系数的阻尼器和一定刚性系数的线性弹簧[4]，示意图见图1。

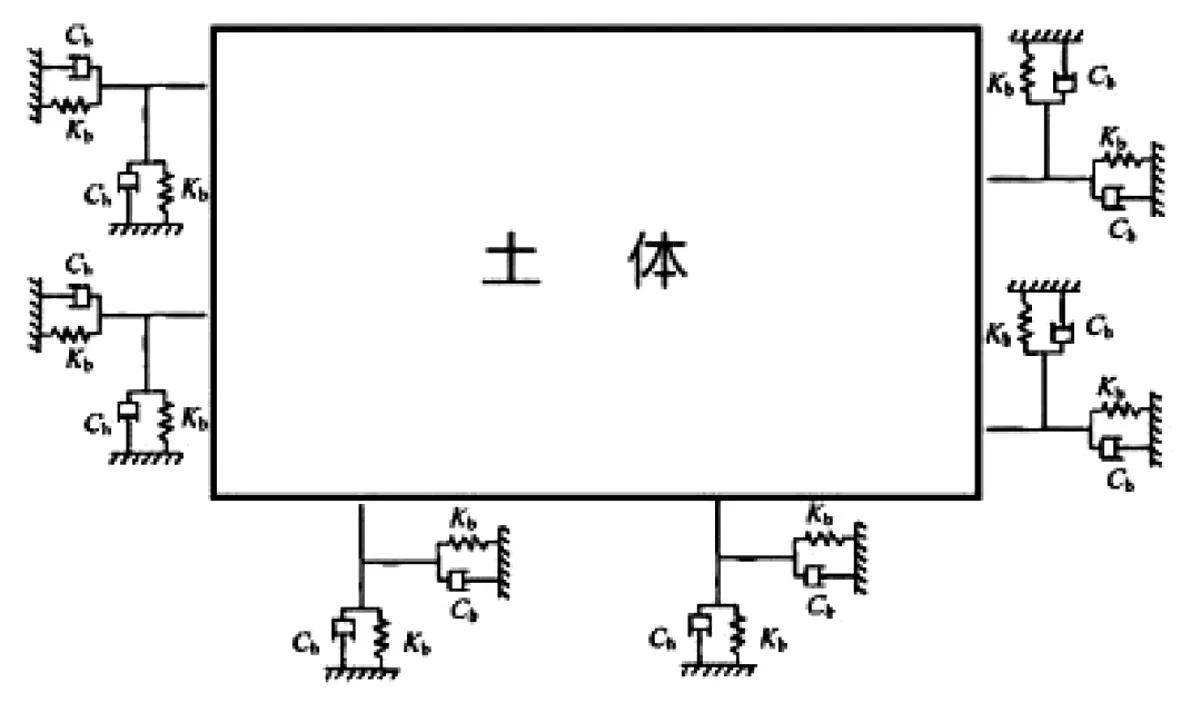
图1 黏弹性人工边界示意图Fig.1 Sketch of viscoelastic artificial boundary

在土-地下结构动力分析中推导出人工边界条件，假定散射波为柱面波，柱面波运动方程为[5-6]：

(3)

(4)

式中：cs为剪切波速；G为剪切模量；ρ为介质密度。

柱面波可以近似的表示为：

(5)

利用方程(3)(5)进一步推导出任一半径rb处的微元面上剪应力同该处速度和位移关系可以表示为如下形式：

(6)

方程(6)的物理意义是：如果在半径rb处截断介质设定人工边界，则需要在截断的人工边界上施加一定刚性系数的线性弹簧和一定阻尼系数的黏性阻尼器两类物理元件，将方程(6)中的系数用弹簧刚度系数Kb和阻尼器的阻尼系数Db来代替，这样就得到了黏弹性边界的边界条件，即为：

(7)

Db=ρ·cs

(8)

其中：rb是黏弹性人工边界上节点至波源的距离；Kb和Db分别是人工边界上的弹簧刚度系数和阻尼器的阻尼系数。如果r无穷大，则黏弹性边界退化为黏性边界。

1.3 固定人工边界

固定边界条件也称Dirichlet边界条件/狄利克雷边界条件/第一类边界条件，是假定在人工边界上位移和转角都为零，那么边界上能量没有被吸收全部反射，反射系数为-1，给出未知函数在人工边界上的数值。人工边界需要土体一般为地下结构的20～30倍，参与有限元计算的土体范围相比无限元边界和远置边界，有限元离散单元数少很多，计算工作量小很多。

对于偏微分方程，∇2φ+φ=0，域Ω⊂Rn的狄利克雷边界条件采取形式：

φ(x)=f(x)，∀x∈∂Ω

(9)

其中f(x)是在边界∂Ω中定义的已知函数。

Dirichlet边界条件常用于机械工程和土木工程(梁理论)中，梁的一端保持在空间中的固定位置。在多物理场仿真ABAQUS软件中，Symmetry/Antisymmetry/Encastre(对称/非对称/端部固定边界条件)、displacement/rotation(位移和旋转边界条件)取值为零，就可以固定相应的位移或转角自由度，达到边界固定的目的。

2 相互作用

在进行有限元分析过程中，对结构与土体间相互作用的数值模拟，通常根据所掌握的数据资料采用土弹簧法、PSI单元法、接触面法等[7]。在ABAQUS软件的接触数值模拟中采用接触面法，建立管道和土体的实体有限元模型，在各个构件上建立接触表面集(surface集)，在各个表面集上利用interaction模块来定义管-土接触对、接触对属性，采用单纯的主-从接触算法，最后施加地震时程载荷，完成数值分析计算。

在ABAQUS软件中，结构与土体接触面之间的相互作用包括法向行为和切向行为[8]，当两个构件间接触压力为零或负值时，接触面分离，无法传递法向压力，所以约束消失，这时法向行为的接触称为“硬”接触(图2)，而两个接触面间的相对运动(滑动)和摩擦剪应力则称为相互作用的切向行为。通常有限元数值模拟真实的摩擦行为十分复杂，简化分析后采用默认的罚摩擦公式(图3)，对于理想的粘结-滑动摩擦行为，使用拉格朗日摩擦公式，产生相对滑动时需要考虑静摩擦系数和动摩擦系数，这时可以采用指数衰减关系来模拟。

图2 硬接触的接触压力与接触间隙关系Fig.2 Relationship of contact pressure and gap of hard contact

图3 罚函数的接触压力与接触间隙关系Fig.3 Relationship of contact pressure and gap of penalty function

在ABAQUS软件中，计算极限剪应力[7]采用公式为：

τcr=μp

(10)

计算时，需要指定一个所允许的最大剪应力[7]采用以下公式：

(11)

式中：μ为摩擦系数，σy为土壤的 mises 屈服应力。

主从面选取应遵循：主控表面应为刚度较大的材料组成，主控表面网格划分比较稀疏。基于以上所需遵循原则，在计算分析过程中，刚度较大的管道外表面作为主接触面，刚度相对较小的土体接触管道部分作为从接触面，形成一对接触。

3 实例

3.1 有限元计算模型

进行有限元分析计算通常采用有限元软件ABAQUS，该软件能够求解分析各类结构的静力、动力、线性、非线性问题。钢管采用各项同性的弹塑性模型，采用Mises屈服准则，通常工程中钢管管道长度3～12 m。本研究中的管道长度为6 m，管道与土体计算模型参数见表1。

表1 管道与土体模型参数Tab.1 Model parameters of pipe and soil

基于管道模型、土体模型、管土之间相互作用建立有限元模型，进行网格划分。有限元网格划分时，与管道接触的土体进行网格加密。为了避免主从面穿透问题，划分网格时在管道接触的土体表面网格数量与管道表面网格数量相同。网格控制采用中轴算法、扫掠技术划分。为了缩短计算时间，有限计算区域内，采用细网格划分的线性缩减积分单元。模型中管道与土体计算单元的单元族均采用3D stress类型， 六面体八节点等参元进行离散，管道单元类型采用实体模型C3D8R，土体单元类型采用实体模型C3D8类型。模型总体单元数量17 200个，总体节点数量19 803个。其中，土体模型单元数量16 880个、节点数量19 131个，管道模型单元数量320个、节点数量672个(如图4所示)。

图4 有限元模型网格划分Fig.4 Grid meshing of finite element model

3.2 计算方法

在ABAQUS中，通常的动力反应分析方法有动态显示分析方法(Dynamic Explicit)和动态隐式分析方法(Dynamic Implicit)。常用的分析流程可归纳为3种(见表2)。

表2 动力反应分析流程Tab.2 Process of dynamic response analysis

计算方法采用上述分析流程1提供的方法。对管道采用静力方法分析，计算区域离散单元的尺寸为0.5，静力分析时间步长1 s，获得管道在自重作用下的应力场；采用动力方法分析，施加地震位移时程荷载，管道动力分析持续时间为50 s，计算管道动力响应。

整个载荷历程划分为2个分析步，在第一个分析步(Static，General)中仅施加静态恒载荷，即自重载荷来计算静力分析；在第二个分析步(Dynamic，Implicit)中施加XYZ三个方向的地震时程荷载计算管道的动力响应。

管土相互作用采用接触面法，接触类型为surface-to-surface contact(standard)，滑动方式采用有限滑移。接触属性中法向接触采用罚函数方法，摩擦系数为0.3，切向接触采用硬接触，阻尼方式在linear(standard only)中取值为damp=0.02，clearance=0.0；damp=0.0，clearance=0.01。

3.3 边界与地震载荷

土体介质弹性模量E=20 MPa，密度ρ=2 000 kg/m3，泊松比v=0.25，那么横波波速Cs=63.2 m/s，纵波波速Cp=109.5 m/s。通常管道固定方式分为3种：固定架-限制管道3个方向的线位移和3个方向的角位移；导向架-限制管道2个方向的线位移；支托架-限制管道1个方向的线位移。

土体人工边界静力分析时采用固定边界，水平方向边界u1=u3=0，竖直方向边界u2=0。动力分析时采用黏弹性边界，在人工边界网格节点切线和法线上施加阻尼器和弹簧。本研究选取阻尼器和弹簧类型为连接点与地面方式(见图5)。

图5 有限元模型边界Fig.5 Boundary of finite element model

地震荷载采用人工地震动合成波。为简化计算，地震波选用沈阳市地铁四号线文贸路站-文东街站区间的位移时程荷载，弹性波垂直从下方入射，直接作用在模型底部截面上，加载地震波时位移时程选用50年10%超越概率(设防烈度)时程曲线(见图6)，地震持续时间取为90 s，当地地震设防烈度为7度，设防地震加速度最大值不超过100 cm/s2。本次计算时程荷载加速度最大值X方向52.4 cm/s2、Y方向53.1 cm/s2、Z方向53.6 cm/s2。

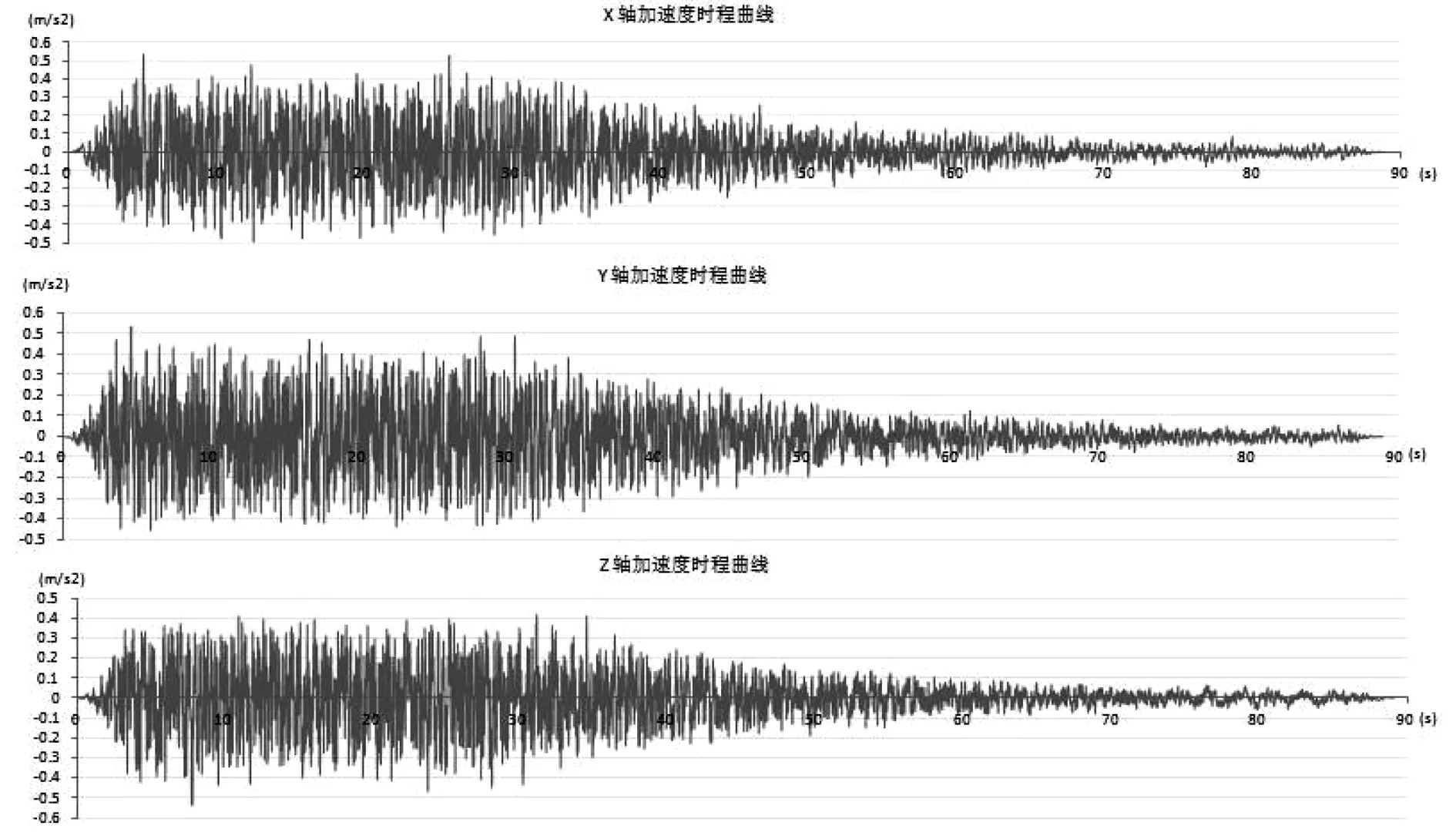
图6 地震荷载时程曲线Fig.6 Time-history curves of earthquake load

4 计算结果分析

为了分析管道不同固定方式的动力响应，分别对4种工况(见表3)下管道的受力性能进行分析，且由于管道自重相对较小，管道周围土体对其约束较大，其应力主要由周围土体的相对位移引起。对于横截面积不大的直管进行有限元动力反应分析，在计算的应力结果中找到整个时间历程中应力最大的单元，提取该单元的整个时间历程曲线(见图7)。

表3 工况列表Tab.3 List of working conditions

图7 四种工况最大等效应力曲线图Fig.7 Maximum equivalent stress curve under four working conditions

通过地应力平衡分析获得动荷载加载前的土体应力云图(见图8)。土体在静力分析时的Mises应力主要集中在下部，应力云图一层层由大到小从下方向上分布，其值在0.05 MPa左右。同时，从图7上可以看出，管道在本次人工地震作用下出现最大应力的时间在step time在4～10 s。最大等效应力的单元、节点分布情况见表4，四种工况计算结果对比情况见表5，其对应时间的管道等效应力云图见图8。管道应力云图显示在靠近固定端部的应力较大，远离固定端部的较小，最大值在140～420 MPa。

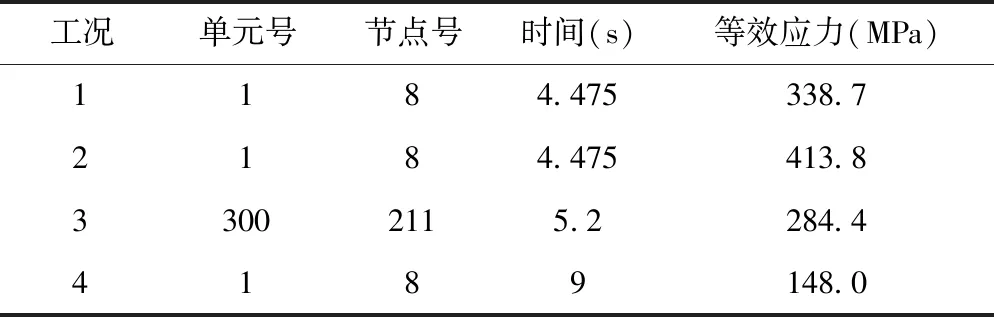
表4 最大等效应力分布情况Tab.4 Distribution of maximum equivalent stress

图8 有限元模型受力分析- Mises应力Fig.8 Force analysis of finite element model-Mises stress

表5 四种工况计算结果对比Tab.5 Comparison of the calculation results under four working conditions

当采用实体模型分析管道动力响应时，模型计算得到了相对稳定、易收敛的结果。计算结果对比显示，直埋无固定管道模型响应最小，最大节点应力仅为屈服应力的35.41%，导向架管道模型响应最大，最大节点应力为屈服应力99%。鉴于地震安全性和工程成本造价考虑，管道铺设最好的方式是直埋无固定管道，其次是支托架管道、固定架管道，最后是导向架管道。实际工程中，可参考当地的地质情况酌情选取支托架、固定架、导向架。通过有限元方法对埋地管道进行应力分析结果对比，选取适合的管道固定方式，既能减少工程成本造价，也能保障埋地管道抗震设防能力，为实际工程提供相应的技术佐证。

5 结论

通过运用大型通用软件ABAQUS，对几种固定方式管道的有限元数值模拟结果进行比对，结果表明，用ABAQUS计算管土地下结构的动力分析是可行且符合实际的。通过以上算例可以看出，通过进行管道动力响应分析，可以查找出最有利的管道固定方式，同时还能找出模型最大应力点，也就是管道的薄弱位置，为城市辅助决策的制定提供有利依据。