混合网络中疾病传播的数值模拟

吴 晓

(海南医学院物理教研室，海口 571199)

复杂网络的研究一直以来都是人们关注的重要课题[1-2]，如复杂网络模型、复杂网络的疾病传播[3-4]与控制、复杂网络的同步[5]等。设计与实际网络更为接近的网络模型是复杂网络的基础。目前，规则网络、ER随机网络、NW小世界网络、Scale-free无标度网络、衰减网络[6]、等级网络[7]等都是比较实际的网络模型。从这些网络特点可以看出，其具有与实际相符的内在演化机制，如规则、随机、偏好、衰减、等级等，因此提出与实际人群关系网络更为接近的网络模型，更能准确反映实际网络的拓扑特性和相关动力学。现实生活中，人群交往在一个小的人群范围内，人与人彼此都认识，他们之间的交往可能按照偏好机制，当人群范围扩大，人与人之间就不可能都认识，那么他们的交往就可能部分是随机的、偶然的，也可以理解为现实网络不仅有节点的偏好连接，当节点增加到一定范围后，也有内部节点的随机连接。

1 网络模型

开始时网络中有m个节点，彼此任意连接(不重连，m=3)。

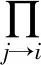
当节点数量大于N0=1000，以p的概率节点增加的偏好连接，以1-p概率节点内部随机连边(不重连)，连边数量与偏好连接数量相等。

网络按步骤循环，直到达到规定节点数量N。

为了与实际网络吻合，内部连边概率不宜过大(p≤0.5)，否则网络会趋近随机网络(也就是p=0)。

2 数值模拟结果与讨论

2.1 度分布与平均度

在有限尺度的均匀网络(随机网络)和非均匀网络(无标度网络)中，平均度与度分布P(k)是网络拓扑结构的重要参数，也是对流行病传播动力学影响比较大的因素[8-9]。从图1来看，当概率p=1时，网络是BA网络，度分布呈幂率分布γ=-3，当概率p=0.7和p=0.5时，偏好连接减小，随机内部连边增加时，度分布P(k)幂率分布的情况不再保持，曲线尾部开始转向随机网络的度分布—泊松分布，也是网络由非均匀网络向均匀网络过渡，其中p=0.7时，网络度分布呈现与实证合作网相同的度分布，由此可以推断实际网络应该是这两种机制共存的混合网络。图2中，当概率p=1时，平均度=6，随着概率p减小，随机内部连边增加，平均度也逐渐增加，且呈非线性变化。

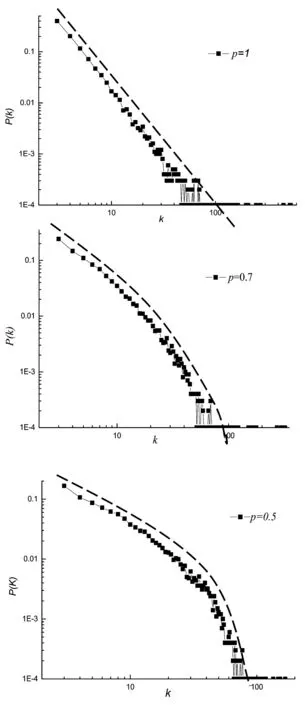
图1 不同概率p下的度分布P(k)Fig.1 P(k) under different p

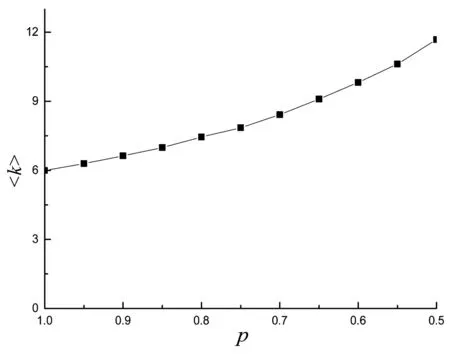
图2 平均度随概率p变化曲线Fig.2 Curve of the changes of with p

2.2 传播动力学

复杂网络上流行病传播动力学基于流行病模型，常见的流行病模型有：SI、SIS、SIR(S 代表易感人群 ，I 代表感染人群，R 为免疫人群)，选取了这三种经典流行病模型进行模拟研究。

2.2.1 SI模型

在SI模型中，总人数N(也就是网络的尺度)被认为是常数，S(t)和I(t)是易感染个体和染病个体的数量，相应的N=S(t)+I(t)。在SI模型中，传播概率被定义为λ, 易感染个体通过其染病近邻个体而被感染，同时，模型中的染病个体始终保持染病状态，不能康复。在SI流行病模型的模拟中，选取了N=10 000，随机选择初始染病节点50个，传播概率λ=0.01进行模拟，ρI代表染病节点数占总数的比例(染病节点的密度)。

从图3来看，随着概率p的减小，随机连边增加，节点染病密度ρI随时间演化曲线保持一致，但流行病蔓延整个网络的时间缩短，p=1,t≈150；p=0.5,t≈100。从三者曲线比较来看，在每一个时间步，p=0.5的概率所占据的染病节点密度最大。因此，此类流行病爆发后，尽量减少与陌生人接触(节点的随机加边)，是控制此类疾病传播范围的有效措施。

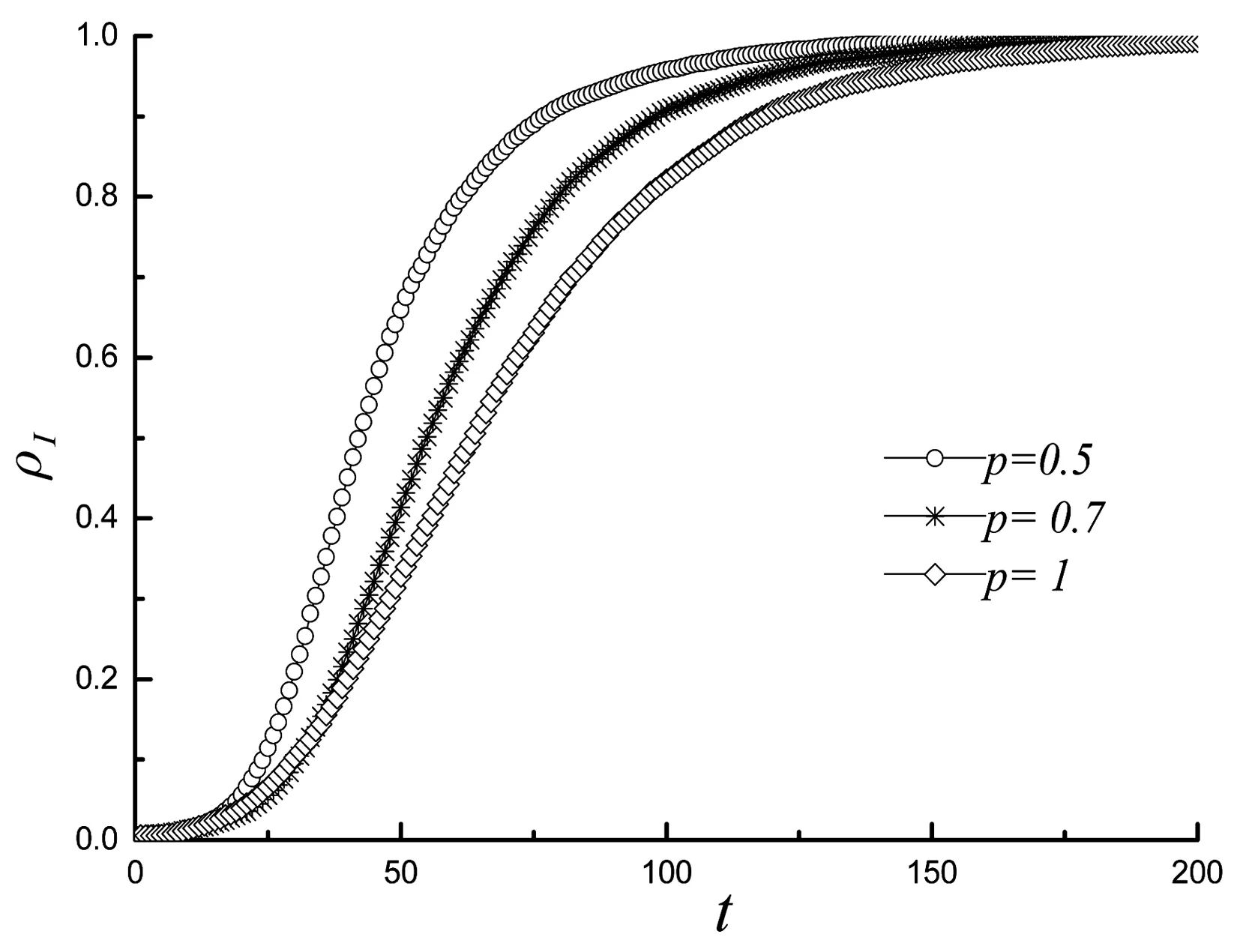
图3 节点染病密度ρ(I)随时间t的变化曲线Fig.3 Changing curve of ρ(I) with t

2.2.2 SIS模型

在SIS传播模型中，个体在网络中的状态是一个循环的过程：易感染态—感染态—易感染态。在每一个时间步，每一个易感染节点被其一个或多个染病近邻以概率ν感染，同时染病的个体以δ(一般情况下，取δ=1)的概率被治愈或再次变成易感染的状态。SIS模型中，有效的传播概率定义为：λ=ν/δ，染病个体的密度(染病个体数目占总人数的比例)ρI。在SIS流行病模型的模拟中，选取N=10 000，随机选择初始染病节点为 50个，感染概率ν，康复概率δ=1进行模拟，有效的传播概率为：λ=ν/δ=ν/1=ν,ρI代表感染节点数占总数的比例(染病节点的密度)。

从图4整体上可以看出，流行病传播到一定时间会形成稳态，疾病以一定的密度ρI维持在人群网络中，不会消失。概率p的变化不影响染病节点密度ρI随时间变化的曲线形态。在有效传播概率λ一定，随着概率p的减小，染病节点形成稳态的密度会逐步增加，从p=1,ρ(I)≈0.08增加到p=0.5,ρ(I)≈0.28。在图5中发现，当概率p减小，随机加边增加，不同疾病传播概率(λ=0.5)情况下，稳态密度随概率p存在近似的线性变化。

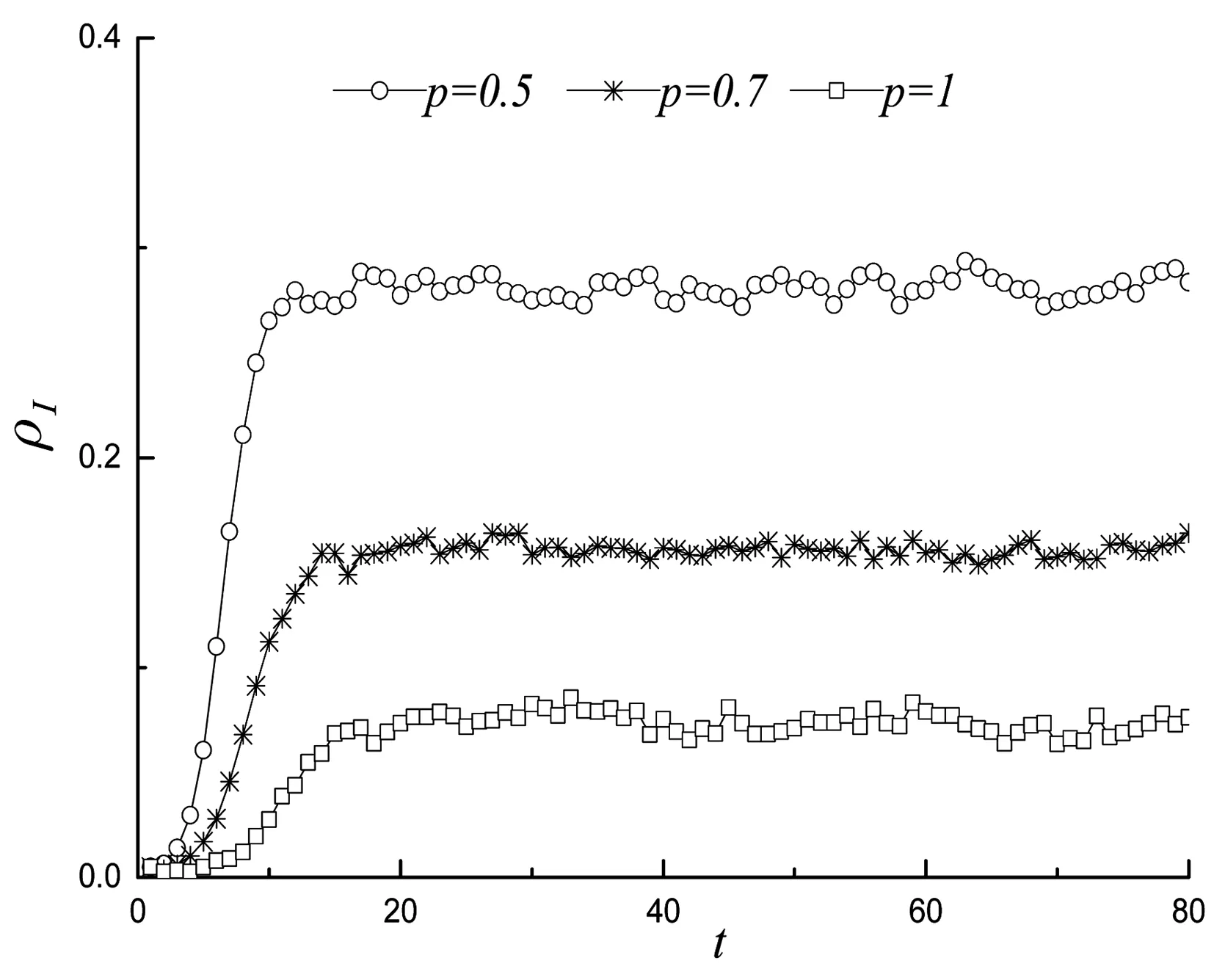
图4 有效传播概率λ=0.1，不同概率p下稳态密度ρ(I)变化曲线Fig.4 Changing curve of steady state density ρ(I) under the condition of effective communication λ=0.1 and different p

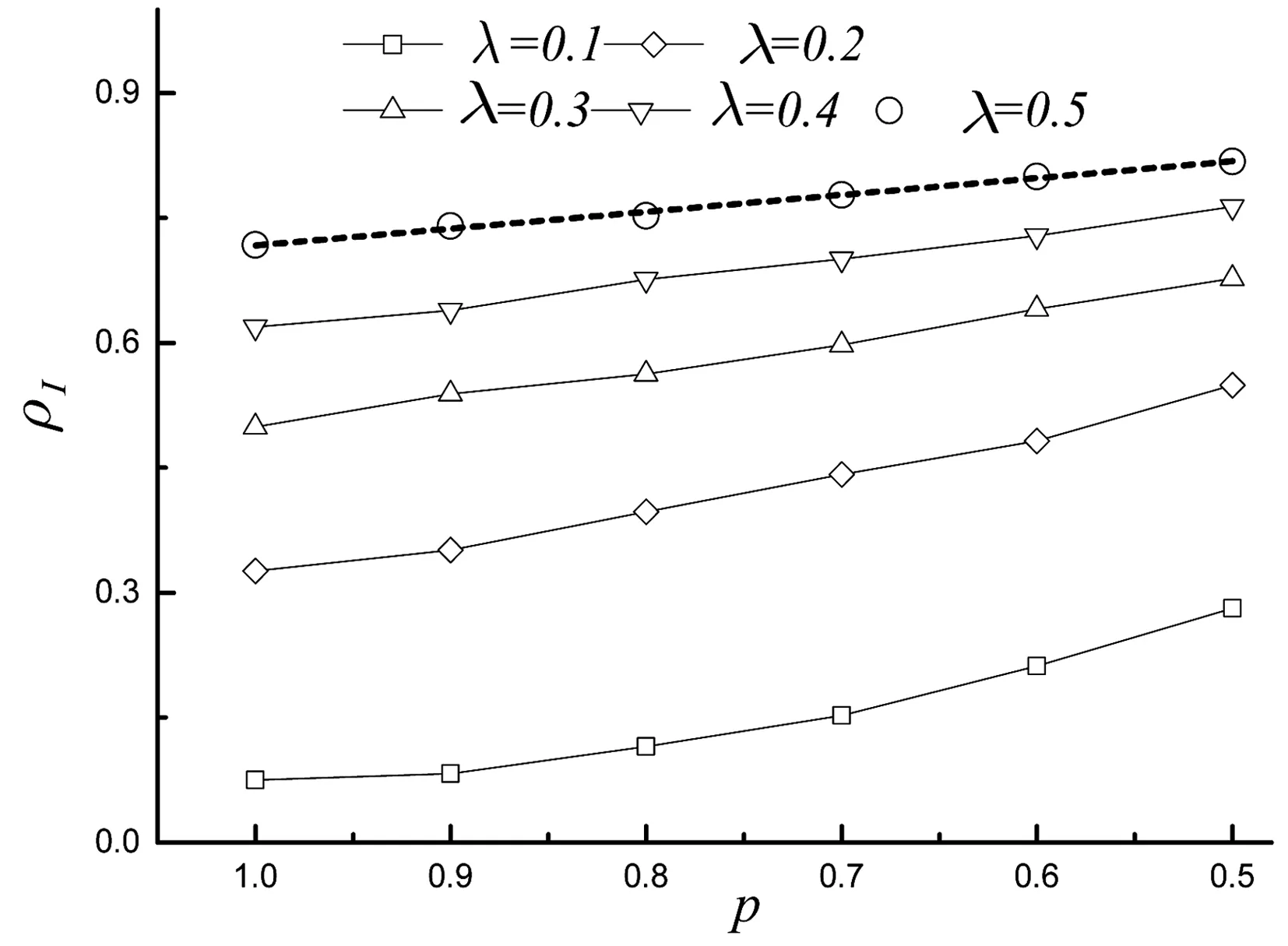
图5 不同概率p下，传播概率λ与稳态密度ρ(I)变化曲线Fig.5 Changing curve of steady state density ρ(I) under the condition of different p and communication probability λ

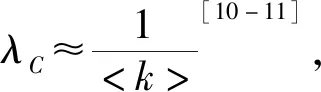
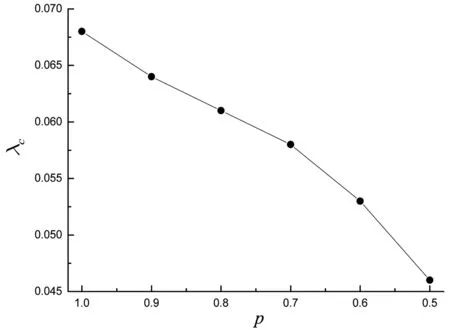
图6 传播临界值λC随概率p变化曲线Fig.6 Curve of spread critical value λC with p

2.2.3 SIR模型

在SIR传播模型中，R为免疫态，即治愈后并获得免疫能力的个体，这类节点不具有传染能力。实际生活中，水痘这类治愈后获得免疫的传染病，往往可以用SIR模型来描述。在每一个时间步，每一个易感染节点被其一个或多个染病近邻以概率ν感染，同时染病的个体以δ的概率被治愈并不再被传染。三种状态个体的密度S(t)，R(t)，I(t)随时间变化的曲线如图7、8所示。选取N=10 000，随机选择初始染病节点为 50个，(1)感染概率ν=0.1，康复概率较小δ=0.02进行模拟，见图7。(2)感染概率ν=0.1，康复概率较小δ=0.3进行模拟，见图8。两者图像整体比较，康复概率较小和康复概率较大，R态呈现出不同的变化曲线。从图7来看，S态节点最终在网络中不存在，网络节点只存在I态和R态，当康复概率较小时，概率p减小，随机连边增加，三种状态整体曲线形态没有改变，S态节点密度在相对消亡时间上有所延长(p=1,t=9；p=0.5,t=25)，I态节点密度减小，R态节点密度近似线性增加。从图8来看，有小部分S态节点存在网络中，当概率p减小，随机连边增加，I态节点消亡时间上缩短，S态节点密度会减小(p=1,ρ(S)≈0.39；p=0.5,ρ(S)≈0.19)，R态节点密度增加，I态节点最终在网络中消亡，网络中只存在S态和R态的节点。可以说，大的康复概率对疾病的消亡更有利，当然这取决于更有效的免疫药物、更好的医疗水平能让病人在短时间内康复。

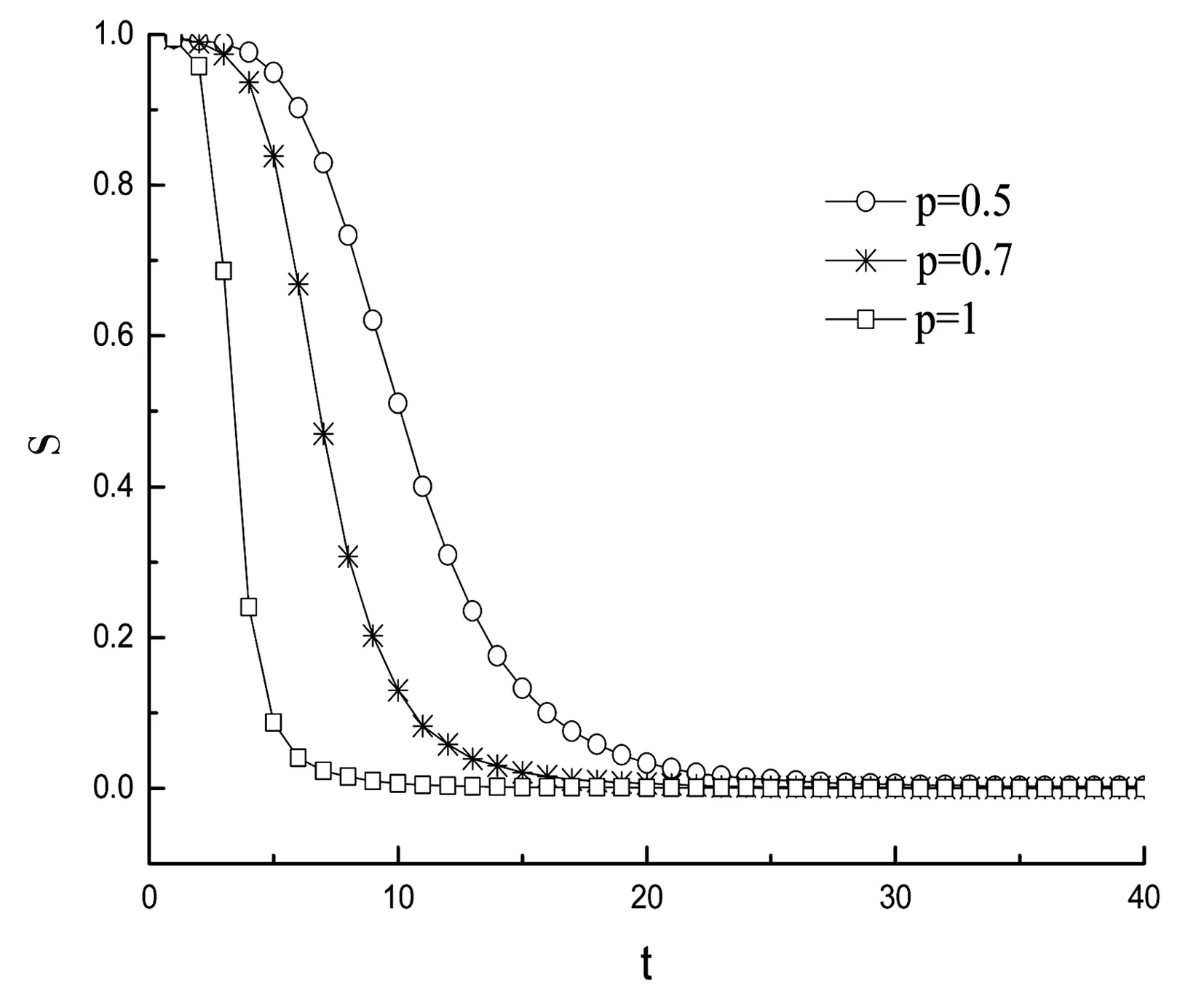
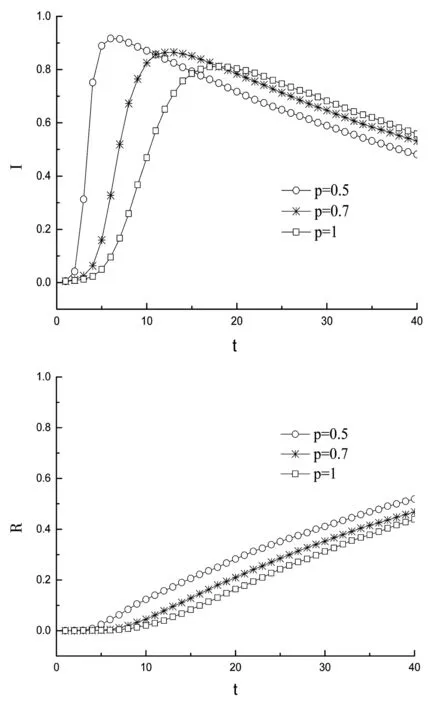
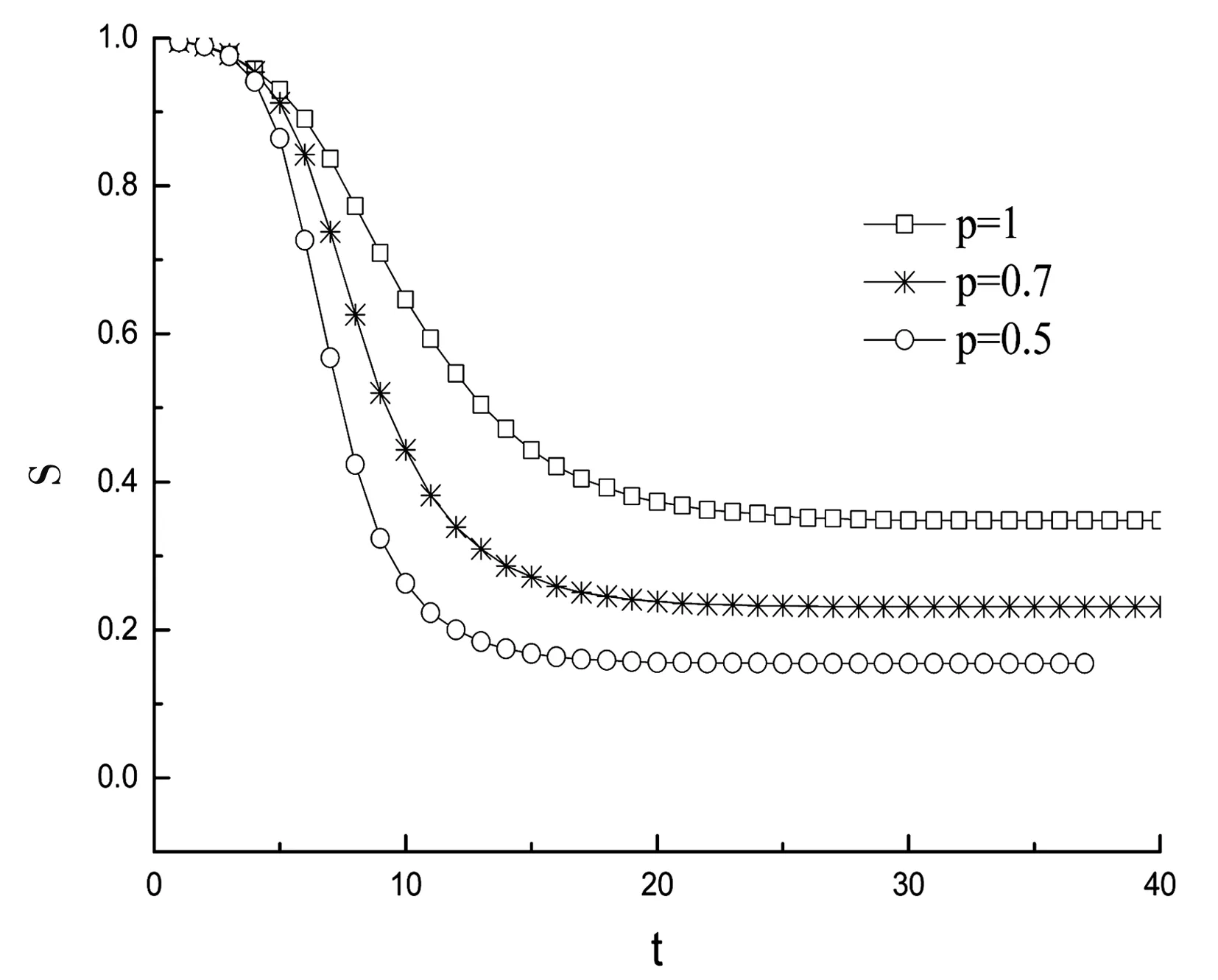
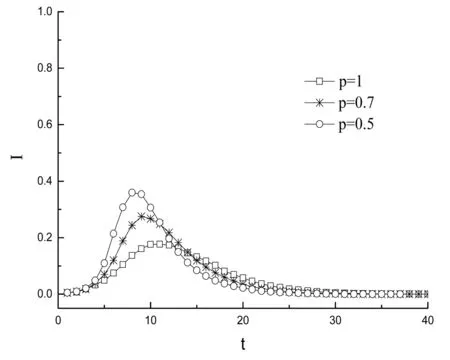
图7 感染概率ν=0.1，康复概率δ=0.02不同概率p下S、I、R态密度随时间变化曲线Fig.7 Changing curve of S, I and R density state with time under the condition of infection probability ν=0.1, recovery probability δ=0.02 and different p

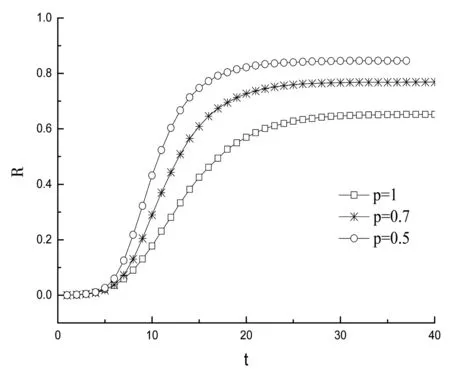
图8 感染概率ν=0.1 康复概率 δ=0.3不同概率p下S、I、R态密度随时间变化曲线Fig.8 Changing curve of S, I and R density state with time under the condition of infection probability ν=0.1, recovery probability δ=0.3 and different p

3 总结

提出随机和偏好机制共存的网络-混合网络，并在此网络上数值模拟流行病传播的相关过程，发现概率p减小，随机连边增加，会带来SI型疾病传播时间缩短、SIS型疾病中节点染病密度增加、传播阈值λC减小等相关不利影响，但在SIR型疾病中会有相反的变化：感染概率一定，较小的恢复概率中，I态密度减小；较大的恢复概率中，I态消亡时间缩短，依此理论来指导实际的疾病预防工作，具有一定的参考价值。