考虑空间变异性的分层边坡可靠度分析

2022-01-20赵炼恒董潇阳胡世红左仕潘秋景

铁道科学与工程学报 2021年12期

赵炼恒，董潇阳，胡世红，左仕，潘秋景

(1.中南大学土木工程学院，湖南长沙 410075；2.湖南铁院土木工程检测有限公司，湖南长沙 410075）

岩土体与钢筋混凝土材料有着本质的不同，由于土体在沉积过程及后沉积过程中经受各种物理、化学作用，使得土体参数在空间上存在一定的变异性。工程实际中，从业者通常将影响区域内的岩土体参数假定为常数，并将安全系数作为评价边坡稳定性的指标，但该种确定性分析方法并不能有效地考虑土体自身固有的变异特征。相比于传统的确定性分析方法，概率分析法能够通过计算失效概率或可靠度并以此来量化边坡的安全程度。近年来，越来越多的学者在进行可靠度计算时将参数的空间变化特征考虑其中。GRIFFITHS等[1]分别使用随机变量法和随机有限元法对黏性土坡的失稳概率进行研究；CHO[2]通过KL展开生成二维随机场模型，将随机场理论与极限平衡法相结合来考虑参数的空间变化特征；HUANG等[3]分析了杨氏模量的空间变异性对隧道衬砌收敛性的作用效应；LI等[4]提出多重响应面法，并研究了不同自相关函数对边坡可靠度的作用效应；GUO等[5]考虑土体的空间变化特征对路堤进行概率分析。尽管众多研究者在岩土体空间变异性方面进行了大量有价值的研究工作，但还是存在不足：以上研究均是研究单一参数的空间变化特征，即参数的自相关性，并没有考虑土体参数间的互相关性；另一方面研究对象过于单一，大部分研究仅考虑单一土层的层内参数空间变异性，忽视了层间参数的变异；此外，在使用随机有限元并结合蒙特卡洛模拟分析可靠度时，需要耗费大量的时间才能得到足够精度的结果。基于此，本文考虑土体参数间的互相关性和空间变异特征，利用Cholesky分解技术生成二维互相关对数正态随机场，通过对ABAQUS的二次开发和引入失效概率变异系数实现对分层边坡的高效随机有限元分析，并结合蒙特卡洛法进行可靠度和参数敏感性分析。

1 随机场模型

1.1 土体参数空间变异性

土体为天然材料，在经过漫长的地质、环境、物理、化学等综合作用后，其性质在空间中存在变异性[6]。为更真实地表征土体在空间中所呈现出的变异特征，需在分析中引入随机场理论。随机场应用的前提是满足平稳性假设，其特征通过均值、变异系数和波动范围来表征[7]。波动范围是与空间变化特征的强弱程度相关的指标，该指标数值越大表明土体参数在该范围内的波动较为平缓，取值越小表明参数波动剧烈。受沉积作用的影响，土体在水平和竖直方向上所表征出的波动范围存在较大差异。通常竖直方向上波动范围要小于水平方向上的波动范围，波动范围的取值由自相关函数确定。本文参数随机场假设满足平稳性假设，考虑自相关结构的各向异性，选取被广泛使用的指数型自相关函数如式(1)所示，用于计算二维平面内任意2点间的自相关系数并组成自相关矩阵K。

式中：τx和τy分别为二维平面内任意2网格中心点间的水平和竖向相对距离，τx=|xi-xj|，τy=|yiyj|，(xi,yi)，(xj,yj)分别表示第i个和第j个网格中心点的绝对坐标，其中i,j=1,2,…,n，n为划分的单元数目，δh和δv分别为水平方向和竖向方向的波动范围。

为将随机场与有限元相结合，需对随机场进行离散。随机场可通过中心点[8]、最优线性估计[9]、局部平均细分[10]、级数展开等方法生成，中心点法计算过程简单便于编程实现，因此本文采用Cholesky中点法对随机场进行离散。土体参数取值不可能为负[1]，将任一点的参数k视作随机变量并服从对数正态分布。确定k的均值uk，变异系数COVk和波动范围，将对数正态随机场表示如式(2)所示：

式中：x,y是参数k的有限元网格中心点的坐标；(x,y)是参数k的标准高斯随机场；ulnk和σlnk的值通过对数正态变换式(3)～(4)求出：

式中：uk和σk分别是对数正态变量k的均值和标准差，ulnk和σlnk分别为正态变量lnk的均值和标准差；COVk为对数正态变量k的变异系数。

通过Cholesky分解技术将自相关矩阵K分解为上三角矩阵ST和下三角矩阵S的乘积如下式：

对于给定的有限元网格和波动范围，K矩阵中的值是确定的，即ST是确定的，此时参数k的标准高斯随机场可表示为：

式中：X={x1,x2,…,xn}为1组服从标准正态分布的随机变量所组成的向量。

1.2 互相关对数正态随机场

在岩土工程中，参数间相互关联，例如黏聚力和内摩擦角呈现负相关性[5]。实际工程中，通常存在着双参数甚至多参数随机场的耦合效应，本文仅考虑黏聚力c，内摩擦角φ的相互作用，且c和φ随机场均采用指数型自相关函数。蒋水华等[11]对生成互相关对数正态随机场的方法已做过详细的研究和描述，这里不做赘述。

2 基于随机场理论的边坡可靠度分析

边坡稳定性分析常用的方法有3种：极限平衡、极限分析和有限元。极限平衡和极限分析在求解安全系数时需假定潜在滑动面，如果在变异性强的土体中，采用这2种方法求解安全系数可能存在误差。为将随机场理论更好地应用于边坡工程，求得更为精确的计算结果，本文采用基于随机场理论的随机有限元法对边坡的可靠度进行分析。

2.1 蒙特卡罗法

蒙特卡罗法以概率论为基础，通过对定义的变量进行随机抽样并计算出每次抽样样本的功能函数。对计算结果进行统计和处理，即可得到失效概率及可靠度。尽管该方法需进行大量的计算工作，但数学公式相对简单，并且不管模型的复杂性如何，该方法具有处理几乎所有可能情况的能力[2]。

首先随机抽取N个随机变量样本，再逐一计算每个样本下的功能函数g(X)，并统计g(X)<0的个数Nf，对于边坡工程，依据边坡的破坏机理建立功能函数为：g(X)=Fs-1。计算边坡失效概率如式(7)，失效概率与可靠度间的关系如式(8)：

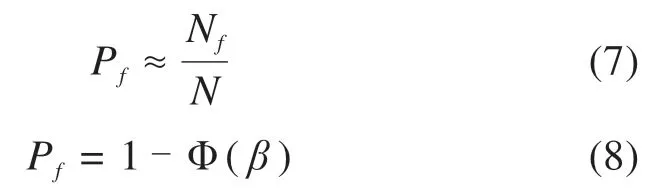
可靠度分析的精度会随样本数量的增加而提高，但过多的样本数量会增加不必要的工作量，为平衡计算精度与求解时间，需确定出合理的样本数量。本文依据中心极限定理，引入失效概率Pf的变异系数COVPf来确定蒙特卡洛模拟次数[12-13]，COVPf定义为Pf的标准差与均值的比值：

蒙特卡洛模拟次数增加的同时COVPf会以的收敛速率逐渐减小，因此可通过选取合理的收敛标准来确定需要的模拟次数。本文将收敛标准设定为0.1，将100组随机场作为一个分析组，在求解出失效概率后计算相应的COVPf，与收敛标准进行对比确定是否需要增加分析组。

2.2 基于ABAQUS平台边坡可靠度分析流程

在ABAQUS中实现随机有限元分析需进行二次开发，ABAQUS为用户提供了2种二次开发路径：一种是利用前后处理层次的Python语言；另一种是利用求解器层次的FORTRAN子程序。在随机有限元分析时涉及到前处理过程中的单元参数赋值；在进行可靠度分析时涉及到后处理过程中的结果数据信息提取及分析；利用Python语言进行前后处理，通过ABAQUS COMMAND将INP文件提交至求解器能减少大量的工作量。此外，Python语言具备简洁、跨平台、免费等特点。因此，利用Python语言进行二次开发更具优势。基于此，本文利用Python语言基于ABAQUS平台实现边坡的可靠度分析。通过Python脚本生成N组互相关对数正态随机场，并结合ABAQUS对边坡进行强度折减确定边坡安全系数。统计功能函数小于0的个数Nf，并通过式(7)～(8)分别计算失效概率Pf及反算可靠度β，实现流程如图1所示。该过程由5个步骤所组成：

图1 边坡可靠度分析流程Fig.1 Slope reliability analysis process

1)建立边坡模型及坐标信息提取。首先在ABAQUS中建立边坡模型并划分网格，在生成的INP文件中提取各单元对应的节点信息并生成相应的节点信息文件和单元信息文件。

2)确定统计参数生成随机场。确定强度参数的均值、变异系数及互相关系数等统计参数，选取指数型自相关函数和波动范围，利用以上信息根据第2节步骤编制生成互相关对数正态随机场的Python程序，并利用第1步生成的节点、单元信息生成N组c，φ互相关对数正态随机场。

3)模型建立、参数输入及获取初始应力场。利用Python程序实现模型建立、参数赋值直至计算全过程并生成初始INP文件，再通过Python脚本更改INP文件中的强度参数批量生成N个赋有随机场参数的INP文件，再通过ABAQUS COMMAND提交批量计算程序得到N个初始应力场。

4)批量地应力平衡。同步骤3，在Python脚本中添加以下语句：场变量及相应参数值、导入第(3)步获取的初始应力场、修改模型关键字，实现地应力平衡并得到最终的INP文件，再通过Python脚本更改此INP文件中的强度参数快速生成N个赋有随机场参数信息的INP文件，通过ABAQUS COMMAND提交批量计算程序得到N结果文件。

5)计算失效概率及可靠度。在ABAQUS中通过运行脚本的方式调用已编写好的Python脚本文件，批量打开结果数据文件并获取到N个边坡的安全系数值，使用EXCEL对安全系数值进行统计，计算出边坡的失效概率及可靠度。

3 算例分析

本文的算例为分层土坡，坡高10 m，坡比1:1.5。几何尺寸及网格划分如图2所示。使用摩尔-库伦破坏准则和非关联流动法则的理想弹塑性本构模型。模型两侧约束水平位移，模型底部约束水平位移和竖向位移，荷载仅考虑土体自重。有限元模型划分有2 071个4节点平面应变单元和2 179个节点，上部土层951个单元，下部土层1 120个单元，单元尺寸为0.5 m×0.5 m。HUANG等[14]建议在随机有限元分析中所采用的单元尺寸与空间相关距离之比应小于0.5，指数型自相关函数空间相关距离是波动范围的一半，因此本文单元尺寸/水平相关距离之比=0.5/1.5=0.33<0.5，满足要求。分别对以下2种情况进行分析：确定性和随机性。基于ABAQUS平台，采用有限元分析不再收敛作为失稳判据。

图2 边坡模型尺寸及网格划分Fig.2 Slope model size and mesh generation

确定性分析时，不考虑空间变异特征，黏聚力、内摩擦角、杨氏模量、重度、泊松比等参数采用均值如表1所示，利用ABAQUS软件求得安全系数为1.210，利用FLAC3D进行有限差分求得安全系数为1.216，两者基本一致。在随机分析时，仅考虑c和φ的空间变异特征，其余参数视为定值，杨氏模量、泊松比、剪胀角等参数对边坡稳定性状态分析结果的影响可忽略不计[15]。本文分析时均假设在不同的土层中土体的参数相互独立，上下2层有着相同的自相关函数、相关系数、变异系数和波动范围，c和φ均服从对数正态分布，均值、变异系数、相关系数及波动范围等参数参考文献[4,16]选取，初步设立随机场参数取值如下：

ρ(c,φ)=0，COVc=0.3，COVφ=0.2，δh=30 m，δv=3 m，用于检验所设置的收敛标准是否合理，土体的参数值如表1所示。

表1 有限元模型土体参数Table 1 Soil parameters of finite element model

3.1 收敛标准的检验

可靠度的计算结果是否精确取决于所设置的收敛标准。为检验设定的收敛标准是否合理，采用图2所示的边坡模型，随机场参数如前所述，边坡的物理力学参数取值如表1所示。按第3小节所述步骤计算并统计出不同蒙特卡洛模拟次数下失效概率对应的变异系数COVPf和相应的可靠度β，统计结果如图3所示。从图3中可看出，当COVPf小于0.1时，β逐渐收敛于1.29附近，因此将0.1作为收敛标准能得到足够精度的可靠度结果。

图3 COVPf和β随蒙特卡洛模拟次数的变化曲线图Fig.3 Curve of COVPf and β with simulation times

3.2 可靠度分析

在3.1节的基础上，将计算所得1 000组安全系数进行统计分析并绘制出安全系数散点图和频率分布直方图如图4(a)和4(b)所示。由图4可知安全系数的分布于0.80～1.45之间，安全系数均值为1.13，最大值为1.43，最小值为0.84。1.43对应的临界滑面及参数随机场如图5所示，0.84对应的临界滑面及参数随机场如图6所示，图中灰色的梯度变化代表着参数值大小的变化。由图4(b)中的拟合曲线可知，安全系数服从对数正态分布。由1 000组安全系数求得边坡的可靠度指标为1.30。

图5 最大安全系数1.43对应的临界滑面及随机场分布Fig.5 Distribution of critical slip surface and random field corresponding to the maximum safety factor of 1.43

图6 最小安全系数0.84对应的临界滑面及随机场分布Fig.6 Distribution of critical slip surface and random field corresponding to the maximum safety factor of 0.84

由图4可知，考虑c，φ的空间变异性时，区别于确定性分析，安全系数会受到显著的影响，同一随机场参数下求得的安全系数既可能大于1，也可能小于1，这表明以安全系数作为边坡的稳定性状态评判指标的传统方法存在争议，也表明可靠度分析的必要性。对比随机分析计算出的安全系数均值与确定性分析计算出的安全系数，可看出确定性分析计算出的安全系数要大于随机分析计算出的安全系数均值，这表明传统的确定性分析不能科学合理的考虑土体的变异性，用确定性分析获取的安全系数评价边坡的稳定性可能造成不保守估计。

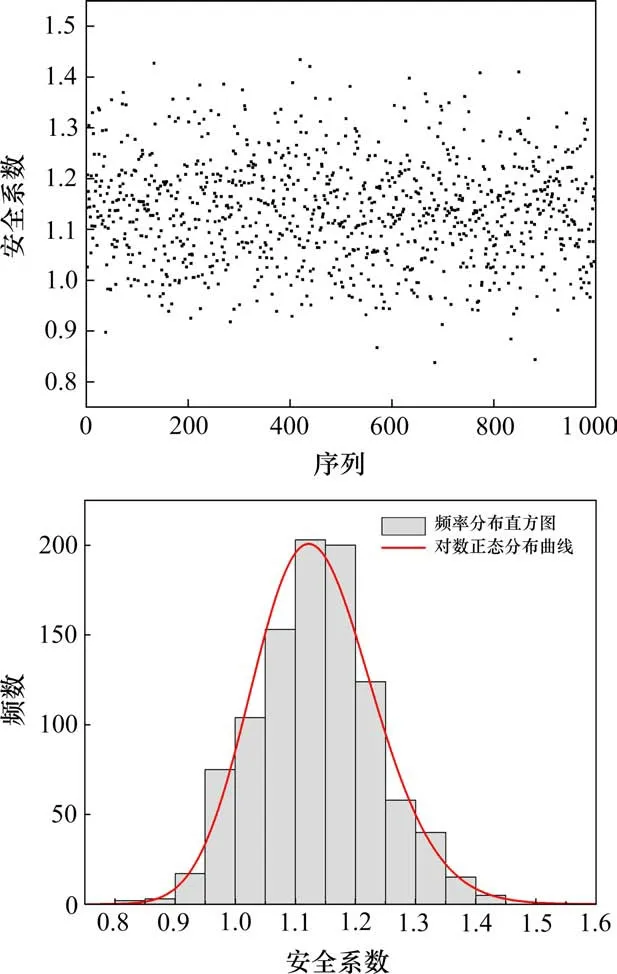
图4 安全系数分布Fig.4 Safety factor distribution

3.3 参数敏感性分析

本小节进行参数敏感性分析，边坡的物理力学参数取值为定值如表1所示，改变2个参数间的相关系数ρ(c,φ)，黏聚力变异系数COVc，内摩擦角变异系数COVφ，水平波动范围δh和竖向波动范围δv，研究随机场参数的变化对边坡的可靠度和安全系数均值的作用规律。

研究表明c，φ间呈负相关性，基于已有文献[2,4]，本文ρ(c,φ)的取值范围为[-0.7,0]，COVc取值范围为[0.1,0.7]，COVφ取值范围为[0.05,0.2]，δh取值范围为[10,50]，δv取值范围为[1,5]，计算不同参数下的可靠度及安全系数均值，结果见图7～11。

从图7中可看出，当ρ(c,φ)从-0.7增加至0时，相应的β从2.457减小至1.298，uF从1.160减小至1.134，β降幅为47.17%，uF降幅为2.27%。这种趋势表明相关系数的改变会对边坡的可靠度和安全系数均值产生显著的作用效应，呈现出负相关性，即β和uF会随ρ(c,φ)的增加而减小，且相比于uF，β对ρ(c,φ)的变化更加敏感，负相关性越强，边坡的失效概率会减小，相应的可靠度会增加，这与文献[17-18]得出的规律相一致。

图7 β和uF随ρ(c,φ)变化曲线Fig.7 Curve of β and uF with ρ(c,φ)

图9 β和uF随COVφ变化曲线Fig.9 Curve of β and uF with COVφ

图8～9分别为COVc和COVφ的变化对β和uF的作用曲线。c，φ负相关时，2幅图中的曲线有相同的走势，β和uF随变异系数的增加而减小。图8中COVc从0.1增加至0.7，相应的β从2.256减小至1.270，uF从1.152减小至1.126，β降幅为43.70%，uF降幅为2.22%。图8中COVφ从0.05增加至0.2，相应的β从2.878降低至2.097，uF从1.184减小至1.150，β降幅为27.14%，uF降幅为2.96%。对比数据，在同一的增幅下，β比uF降幅更大，说明可靠度对变异系数更为敏感。计算图8～9中起末2点斜率的绝对值，分别为1.643和5.208，可看出内摩擦角变异系数对边坡的可靠度影响更为显著。

图8 β和uF随COVc变化曲线Fig.8 Curve of β and uF with COVc

图11 β和uF随δv的变化曲线Fig.11 Curve of β and uF with δv

图10～11分别为δh和δv的变化对β和uF的作用曲线。C，φ负相关时，2幅图的曲线呈现相同走势，随波动范围的增大，参数的变异性减弱，β和uF呈现相反走势，β随波动范围增大而减小，uF随波动范围增大而增大。δh从10增加至50，相应的β从2.409减小至1.927，uF从1.148增加至1.152，β降幅为20.01%，uF增幅为0.34%；δv从1增加至5，相应的β从2.366减小至1.995，uF从1.143增加至1.158，β降幅为15.6%，uF增幅为1.23%。对比分析各项数据，δh和δv均会对可靠度产生显著的影响，对安全系数均值的影响较弱，即可靠度对水平和竖向波动范围敏感。分别计算图10～11中起末2点间斜率的绝对值，分别为0.012和0.092，可看出竖向波动范围对边坡的可靠度影响更为显著。