基于偏振图像融合的接触网U型抱箍螺母松脱检测研究

2022-01-20刘仕兵全丰喻星

铁道科学与工程学报 2021年12期

刘仕兵，全丰，喻星

(华东交通大学电气与自动化工程学院，江西南昌 330013）

近年来，我国高速铁路发展迅速，铁路运行原发性问题急剧增加，弓网之间零件状态正常是列车安全取流的重要保障，当接触网任一部件出现故障时会造成严重的停车事故。4C检测主要采用图像处理技术对接触网悬挂状态进行评估，普通图像因受光照散射影响，对目标信息获取能力差，继抱箍、旋转耳、套筒等部件的故障检测难度持续增大。物体因材质差异其表面导电性不同，当光波照射后表面发生反/辐射电磁波时，其介质特性会改变电磁波的偏振态，相比普通强度图像，偏振探测技术可以挖掘目标深层次多角度细节[1-2]。而偏振技术和信息融合也逐渐成为图像研究热点，定性分析光波偏振态与可见光谱在特征表达上的互补冗余性，通过融合二者来提高成像质量，可对微小部件在粗糙度、边缘连接、灰度梯度和纹理等方面显著增强，从而提高故障检测效率。目前二者有机结合广泛应用于军事探测、野外勘查、遥感信息等领域[3-4]。将偏振技术应用在接触网系统提取目标偏振实时信息，目前该研究尚属空白。在接触网图像处理检测方面，刘凯等[5]利用卷积网络完成承力索底座识别，引入Beamlet变换用局部链搜索算法提取裂纹信息，但其线段基的阈值Tf难以确定会产生搜索偏差；王佳祺[6]采用超分辨率重建对开口销图像去模糊处理，构建实力分割对螺母松脱进行检测，该方式对训练样本像素要求极高；陈隽文等[7]用Hough直线和边缘检测将螺钉与主体分离，采用像素累加判断螺钉不良状态，其分割过程受光照因素影响大；韩烨等[8]探讨旋转双耳故障，提出SIFT特征匹配和边界曲线弯曲度来判断是否断裂，但故障倾角不明显。上述方法都存在图像质量不高，检测流程过于复杂等问题。自从WOLFF等开启研究光的偏振领域，ZHANG等[9]提出一种无监督的深度网络来优化偏振图像，该网络以端到端映射用定制的体系结构和损失函数来提高视觉质量。KIM等[10]提出构建segNet和DCGAN深度学习模型，通过小波融合RGB新的分量来提高图像信噪比。NAIK等[11]提出一种动态随机共振DSR指标来引导小波融合过程，达到图像增强效果。ZANG等[12]提出低频以PCA，高频基于局部能量的双树复小波融合方法，但细节信息表现不佳。接触网U型抱箍作为绝缘子与腕臂间重要扣件，其松动会引发严重的弓网事故，为改善目标成像质量，增大视觉可读性，在总结前人基础上，本文提出将偏振技术应用到抱箍图像采集上，并对常规小波融合在高低频系数重构规则上进行优化提升，将融合结果与DCT，NSCT和NSST等方法比较，计算图像各项评价指标。在检测阶段提取融合图像的LBP特征值映射至二维向量空间，利用cosine相似度分别对抱箍螺母正常、松动和脱落3种状态进行检测，并利用耦合网络对该状态下单像素迭代点火进行验证，根据其迭代次数及熵值比的反馈差异来检测算法的准确性。

图1 U型抱箍结构Fig.1 Structure of U-shaped hoops

1 偏振理论

1.1 光波偏振态

目标物体由于反射和辐射光波存在偏振特性，根据物体材料、粗糙度等理化性质能对目标纹理、边缘、阴影进行清晰成像，增强目标与背景对比度。通常以斯托克斯矢量stokes=(I,Q,U,V)T来描述光波全偏振信息，I为光照总强度，Q为水平方向上线偏振光，U为对角方向上线偏振光，因大气散射圆偏振光分量极少，所以V在实验中不予考虑。在二维平面上当偏振片与X轴成夹角θ时，入射光透过镜片此时光电仪可测到该角度下光照强度Iθ，Stokes总光强理论公式为

式(1)中：当取0°，45°，90°，135°4个角度下拍摄可得到4个分量光强，此时偏振光各分量可描述为

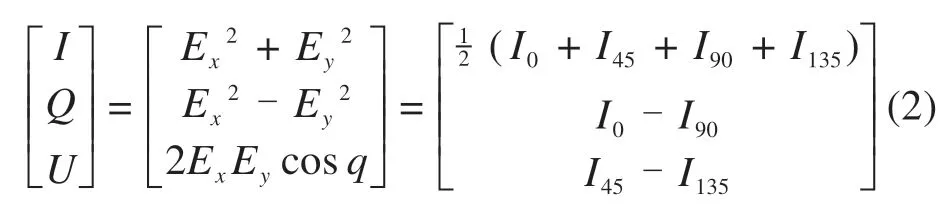
当反射光透过偏振片成像后，根据偏振光线传播理论求得目标线偏振度图像(DOLP)以及偏振角图像(AOP)：

其中：0≤DOLP≤1，表示线偏振光占总光强比例，偏振角为偏振光分量振动方向与参考方向夹角θ，其范围为0°≤AOP≤180°。

1.2 偏振成像模型

描述光波在物体表面作用后反射产生的偏振效应，利用微面元物理模型对光线传播进行反演，提出偏振双向分布函数BRDF，其表达式如下：

当光线波长为λ时，Lr为Stokes矢量下反射光能量，Ei为入射光能量，且BRDF实际为极小通量，光波能量为有效平面的均值，F为4阶穆勒矩阵。当光线照射目标后发生反射偏差产生光波偏振态，原理作用与矩阵中的δi，ϑi，δr，ϑr相关，即入射/反射光的方位角和天顶角。实际成像过程通过偏振片P1和P2来模拟穆勒矩阵达到偏振状态。

图2是偏振主动成像模型，利用光源透过起偏器P1(偏振片代替1/4石英薄片)产生全线偏振光，入射角度为ϑi的线偏光照射到目标表面，其光线反射角ϑr经过偏振片P2在传感器上成像，即PSA探测仪。在实际偏振图像采集中，需要旋转偏振片P2在0°，45°，90°和135°4个相位角下得到不同光波偏振态的目标信息参量，进而利用仿真视觉合成偏振信息图。

图2 偏振系统成像Fig.2 Images system of Polarization

2 图像融合

2.1 小波变换

随着小波变换算法Mallat发展应用，将图像分解与重构在时频之间转换，通过伸缩和平移对分解信号进行多尺度详细分析，广泛应用于图像处理、信号重构等领域[11-12]。图像处理采用离散二维小波(DWT)将信息转换并分解，信号在固定尺度下平移构成Φ(2Jt)空间，形成尺度向量组。每一尺度空间下的细微变化向小波空间投影得到小波向量组，该时间刻度下展开得到尺度系数ΦJK(T)和小波系数φJK(T)。

当信号在尺度空间做卷积得到低频子带，决定图像大致轮廓为近似系数；信号在小波空间卷积得到3个方向上高频系数为表现细节过渡边缘等。图像经N层分解后二维信号变成3N+1个子带系数，利用多尺度小波重构各方向上子带系数逆变换得到新图像。

2.2 PCNN耦合神经网络

根据猫大脑视觉皮层细胞工作原理，Eckhom提出了由多个神经元脉冲链接的单层反馈型网络[13]。在二维图像实时处理环境中，具有空间邻近和特征相似聚集特性，能对像素形成全局耦合和脉冲点火同步发生。该网络由接收域、调制链接、脉冲激发3部分组成，且接收域由包括外部刺激等3路信号构成，进行点火迭代时像素点相当于神经元与其逐一对应，而主要点火控制则由脉冲发生器中活动总数和电容积分共同决定，各区域工作理论表达式如下：

式中：为反馈输入；为外部输入，是分解后图像在k尺度任意方向(i,j)位置的低频子带系数；

2.3 本文融合规则

融合规则对图像重构起决定作用，由于小波变换方向有限且平移存在畸变，在处理时低频信息会被平滑过滤，利用db4母小波将强度图I和偏振特征图F进行4层分解后，在低频系数融合中引入PCNN网络对像素点耦合点火，高频系数则以改进的空间频率MSF作为依据进行重构。

2.3.1 偏振特征融合

偏振角与偏振度在特征表达上各有优势，为保留有效信息，定义互信息(MI)为融合权值：

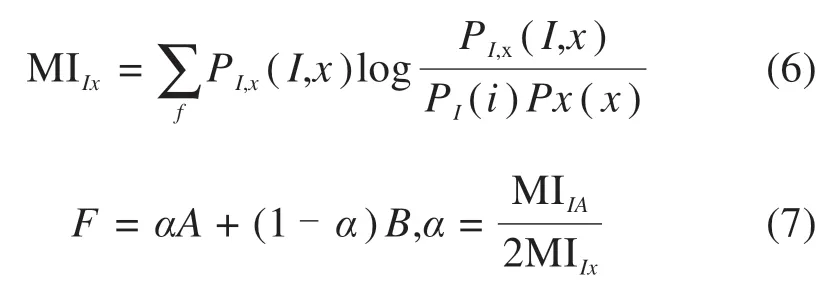
式中：PI,x(I,x)为模板与单一源图像的联合边缘密度；PI(i)和PX(x)为强度图I和源图边缘概率密度；α为融合加权量；A和B对应偏振参量，确立源图像互信息变量并加权融合得到偏振特征图F。

2.3.2 低频系数融合规则

低频系数反映图像灰度信息变化较平滑的轮廓部分。将分解后低频系数灰度值作为PCNN输入，图像区域能量设定为链接强度β，根据源图像点火频率图选择待重构的低频系数。

1)β设定，如果将链接强度设为某一固定值，在图像处理中对像素区域特性反馈差，像素点间关联性因β导致迭代后图像对比度降低，考虑到局部关联对系数重构有较大影响，而区域能量E能反映局部像素灰度差变化，故将其作为链接强度β=E。计算规则如下。

选取3*3窗口作为能量子块，其像素灰度乘以卷积权重，对图像遍历后得到每一子域能量矩阵。

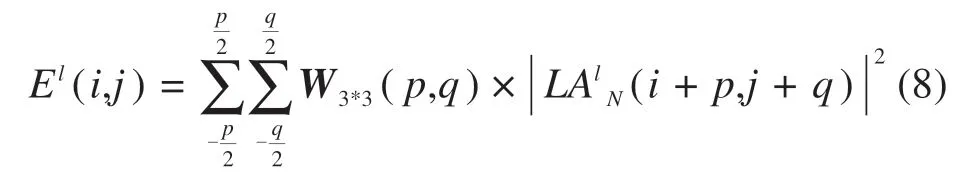
LAN是小波分解第N层，W3*3是该区域对应卷积系数矩阵，设中心像素点为(i,j)。El(i,j)为图像在L尺度下区域的p×q低频系数对应的局部能量和。

2)当区域能量较大时表明窗口包含信息多，此时近似像素点满足被捕获范围将产生兴奋提前点火，并实行自适应调节。每层低频子带系数经n次迭代后总点火次数为

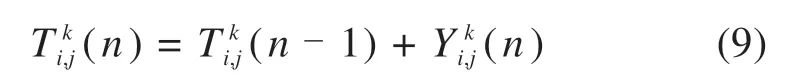
将该子区域映射图归一修正得到点火频率图

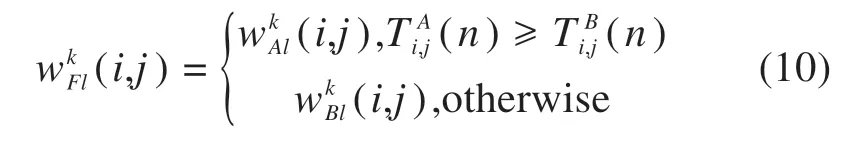
2.3.3 高频系数融合规则

高频系数是视觉感官梯度变化的敏感部分，多数研究选择高频子带时忽略分解后具有方向性。为避免丢失细节，根据这一特性引入空间频率MSF，分别计算源图像高频子带各方向上的行频率(RF)列频率(CF)及对角频率(DF)，计算如式(11)所示。

分解后在图像M×N区域当中，空间频率定义如下：

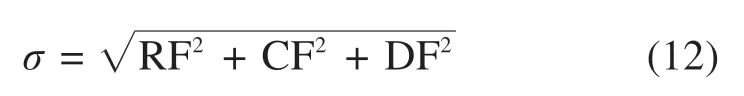
分别获得强度图I空间频率和偏振特征图F空间频率，高频系数选择规则如下：

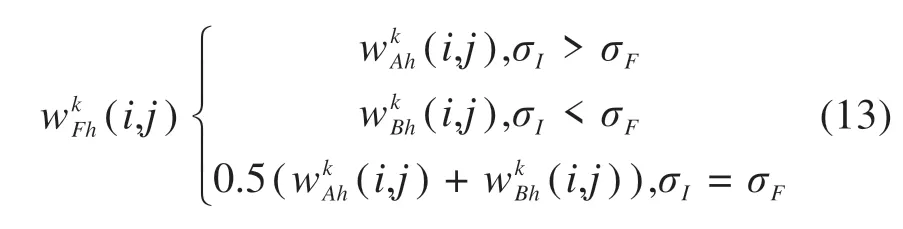
经σI和σF比较后选择待重构高频系数，最后整合新的低频系数(i,j)和高频系数(i,j)进行小波系数重组，对其逆变换得到融合的新图像。算法总体融合规则见图3。

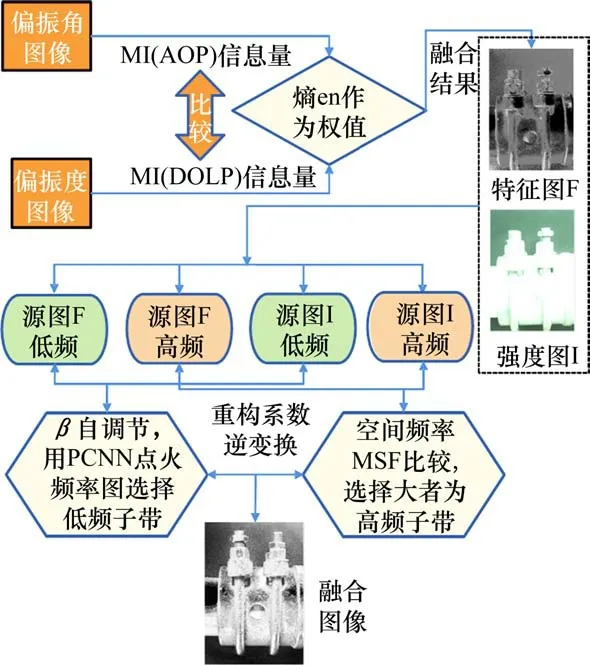
图3 总体融合流程Fig.3 Entire process of images fusion

3 螺母松脱检测

U型抱箍结构以双螺母固定，列车运行时剧烈震动导致螺母松脱，但体积过小视觉判断极其困难。利用偏振融合图像对目标轮廓、纹理做增强处理，采用加速稳健特征检测(SURF)对螺母区域初定位，提取螺母局部二值特征量(LBP)，将其变换为cosine向量后对松脱状态进行相似性测定。

3.1 提取螺母特征量

SURF特征匹配算法是目标提取的重要工具，该算法引入Hessian矩阵和盒式滤波器来提高匹配速度，同时配对特征点准确率增加。首先提取螺母区域分3个步骤。

Step 1：求取抱箍区域积分图像，引入选用2阶黑塞矩阵作为滤波器与核卷积计算2阶偏导数。

Step 2：改变滤波盒子尺寸与图像积分检测纹理，求取矩阵不同响应值并对极大抑制。

Step 3：利用harr小波对图像进行梯度运算，响应值加权后分配主方向θω，沿主方向将区域分块，计算4个特征向量Σdx，Σ|dx|，Σdy和Σ|dy|，根据纹理差异对待检图像进行特征点匹配。

依据黑塞矩阵迹判断特征点方向，采用欧式距离对2幅图像进行配对。图4(a)为目标与整体抱箍特征点配对，融合后匹配度明显增强；根据模板角点确定特征区域尺寸，对区域4个顶角坐标从左至右依次进行读取标定，并主动绘制螺母定位框，如图4(b)所示。

图4 定位螺母模板Fig.4 Locating nut template

判断螺母松脱状态与其结构位置相关，本文摒弃直接以灰度值做余弦测量的判断方式，加入对光照、角度鲁棒性强的旋转不变局部二值模式(LBP)。首先提取待测图像与模板图像LBP特征值，该算法对图像局部纹理特征描述灰度不变[15]。利用其改进模式圆形算子在图像n×n区域内采样P个像素点，其采样半径为R时，特征量如下：

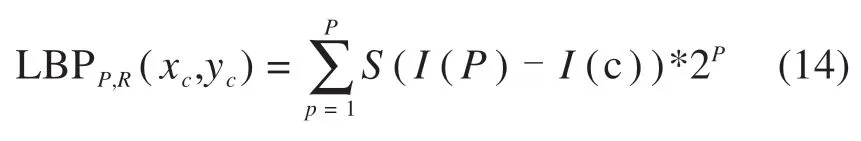
取边界上第p个采样点，将其灰度值与中心点比较，根据差值进行定义0/1特征值，形成一个二进制序列。当半径为1，采样点为8时，产生256种特征模式，且像素点与LBP值相对应，对数字编码做旋转位移，选择位移特征值中的最小值：

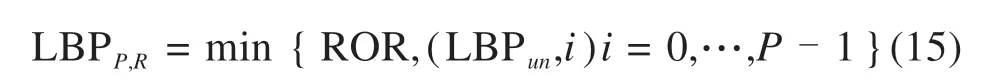
式中：LBPP,R即为该采样区域内最小值，取其作为局部特征值，特征模式转换原理如图5所示。

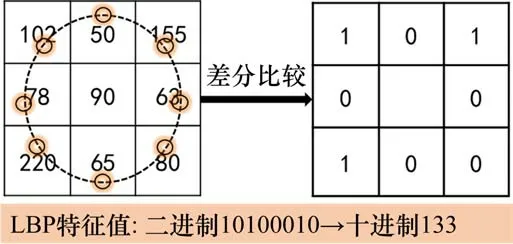
图5 特征模式变换Fig.5 Conversion of feature modes

3.2 故障状态检测

对图像进行特征变换后将其值映射到二维空间L(ρ,θ)中，再以向量间余弦角作为诊断原则，当余弦值趋近1则图像结构越相似，趋近0时则差异越大，且每个像素特征值对应一个元素。设模板图像为a=(α1,α2,α3,…,αn)，待测图像为b=(γ1,γ2,γ3,…,γm)，对a，b间余弦角进性相似性比较，度量公式如下：

以模板向量为基准，通过计算所得余弦值间差异评判故障等级。当松脱时螺母间距d变化，偏振信息在位置上表达可能存在暗影，曝光等，针对螺母间是否存在故障进行相似性实验，过程如下：

1)备螺母缓慢旋转直至脱落，得到多组余弦值cosθ1，cosθ1，…，cosθm，当松动时根据多组值域范围作为判定依据；

2)脱落时测量多种状态下余弦值cosθ1，cosθ1，…，cosθn，取最小值作为判定截止量。防止位置移动、光照变化、拍摄抖动、背景变换等因素影响度量结果。

3)本次试验中对抱箍螺母脱落样本35例，对存在松动现象的样本100例分别进行实验，统计余弦值并做归类，其故障判定原理如表1。

表1 故障判定原理Table 1 Principles of fault judgment

判定范围每组数据取少许裕量，且仅当待测图像为原模板时其余弦值取1。

4 实验分析

4.1 目标偏振采集

采用偏振分时方式对U型抱箍进行成像采集，严格把控拍摄周期，防止光照推移影响采集效果。传感器采用大恒图像产MER-10GC型彩色成像，像元尺寸为1.67 μm，分辨率为1 000万像素，GPIO供电触发线连接，镜头型号LM16焦距16 mm。偏振片为EDMUN公司产，型号85-919直径25.6 mm线偏振片。缓慢旋转偏振片在4个角度下获取偏振信息图像后，根据式(2)，式(3)和式(7)在Matlab上合成强度图I，DOLP，AOP及偏振特征图F。

4.2 图像融合及评价

图6为初步仿真结果，图6(a)为强度图I，具有强曝光度；图6(b)为偏振度图像，反映部件结构轮廓；图6(c)为偏振角图像，反映纹理、沟槽、边缘交接等细节；图6(d)中偏振特征图F集中反映多层次信息，对背景抑制和工件去高光作用效果明显。

图6 偏振信息图Fig.6 Polarized information images

按照本文算法对光谱与偏振图像改进融合，同时与文献[12-14]中5种常见融合方法进行比较，仿真结果图7所示。在视觉上已有明显差异，但深度细节无法评判。为更好评价本文算法优势与不足，采用熵En，平均梯度AVG，标准差STD，均方误差RMSE及结构相似度SSIM 5个图像评价指标对6种融合方法进行数据提取。待测图像大小为M*N时，前3个指标计算如下：

图7 不同融合方法比较Fig.7 Different fusion methods were compared

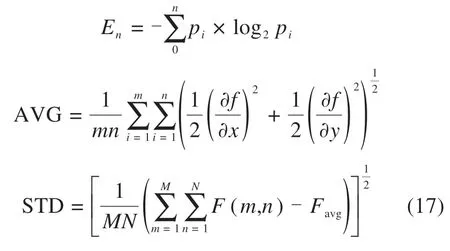
熵、梯度及标准差越大代表反差越大，可利用信息量增多；均方误差越小代表图像整体性良好，结构相似度则是衡量与源图像相似程度。在Matlab视觉平台上输入不同融合图像，按照理论公式计算评价指标如表2。

对融合结果进行比较分析，图7(a)为空域PCA主元成分进行融合，熵5.79最低，丢失信息较多，因图像灰度弥散导致标准差和平均梯度急剧增加，为77.3和0.178，该结果不予考虑。图7(b)为金字塔采取局部能量进行融合，平均梯度0.107，灰度指数较集中，对偏振信息表达较少。图7(c)是常规小波融合方法，低频加权，高频基于区域能量最大，由于缺乏局部表达其灰度差为57.96，梯度0.108，对比度一般，且含较多噪点。图7(d)利用非下采样轮廓波(NSCT)融合，熵值7.70，信息量较多，平均梯度0.064，细节极差故融合后其边缘变形严重，部分轮廓消失。图7(e)采用非下采样剪切波(NSST)融合，灰度差48.32和平均梯度0.056，指标数最低，导致边缘连接性强块状明显，SSIM为0.57故结构失真严重。图7(f)采用本文改进算法，其中PCNN参数设置如下：VL=1，Vθ=20，αL=0.07，αθ=0.2，N=200，W=[0.707 1 0.707;1 0 1;0.707 1 0.707]，β依据区域能量自适应选取。仿真结果视觉性能良好，熵为7.83，增加1.7%；平均梯度0.131，标准差73.87，说明抱箍纹理细节明显增强，对比度显著增大；结构度为0.92最高，像素均方误差为49.86最低，说明融合图像从源图像中保留有效信息多，轮廓信息保留完整。表2中数据充分说明本文算法融合图像灰度级更分散反差更大，且能消除部件高光反应及背景干扰，符合机器视觉处理要求，达到全域增强的效果。

表2 评价指标结果对比Table 2 Comparison of evaluation index results

4.3 检测结果分析

通过上述图像融合增强局部细节后，用相似性度算法检测主、备螺母差异准确排查故障源。对采集装置进行校准、补光处理后采集线路上100张U型抱箍作为实验对象，其中螺母松动15例，备螺母脱落7例，正常78例。采用上述算法对融合图像进行故障判断，在相似度计算中有13例样本测量范围值在0.86～0.94间，7例样本测量范围值在0.76～0.83间，有2例故障因PSA装置抖动导致无法评判，样本误测为7例，故障统计分布见图8，通过数据验证该方法故障检测率约为90.9%。同时与文献[16]中故障检测方法进行比较实验，检测精度和速度对比如表3所示。

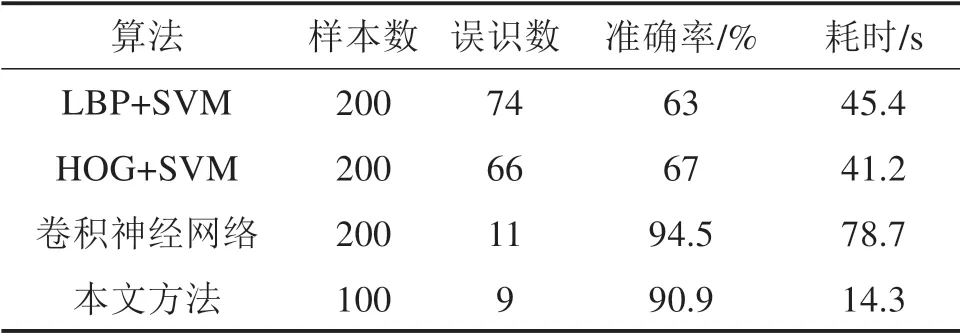
表3 故障检测算法对比Table 3 Comparison of fault detection algorithms

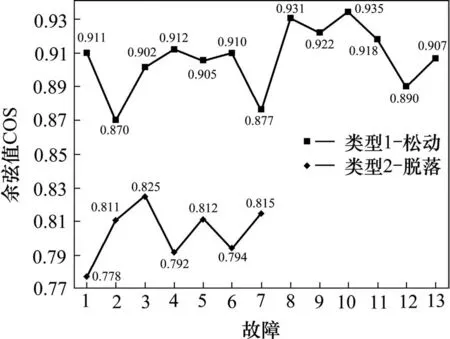
图8 U型抱箍故障情况Fig.8 Fault conditions of U-shaped hoop

前2种手动提取算法过程繁杂，数据训练耗时且样本采集偶然因素多；CNN方式在特征提取方面压缩工作力度，但对设备硬件要求极高同时训练耗时增加。而本文利用图像增强和相似性原理检测后，在时间和准确率上显著提高，目标处理快捷简易，优于机器学习算法。同时利用耦合神经网络从上述样本中选择正常、松脱程度不等、脱落3种故障情况进行像素迭代点火，结果如图9(a)～9(e)所示。其结构差异性导致在迭代时最大熵值比在0.501～0.630之间，迭代出现波峰次数及熵值比各有异同，表明区块内灰度等级不一，像素迭代曲线趋势明显不同。当脱落时迭代次数为3，松动状态次数为4，证明螺母脱落时故障严重，由此交叉验证本文算法在检测实验上的准确性，表明该故障诊断原理在U型抱箍螺母松脱检测上良好实践效果。