考虑随机需求和硬时间窗的多目标车辆路径优化方法
2022-01-20陈治亚高辉徐光明刘吉华
陈治亚,高辉,徐光明,刘吉华
(1.中南大学 交通运输工程学院,湖南 长沙 410075;2.五邑大学 轨道交通学院,广东 江门 529020)
带时间窗的车辆路径问题(Vehicle Routing Problem with Time Windows,VRPTW)是在车辆路径问题(Vehicle Routing Problem,VRP)基础上衍生出的组合优化问题。可描述为:一列车队从配送中心装载产品后,向指定客户分送货物,在满足客户时间窗、限载量等约束条件下,规划一条最优路径,达到诸如成本最小、路程最短等目标。时间窗约束的VRP问题[1-2],可分为软时间窗VRP(VRP with Soft Time Windows,VRPSTW)、硬时间窗VRP(VRP with Hard Time Windows,VRPHTW)、模糊时间窗VRP(VRP with Fuzzy Time Windows,VRPFTW)。例如,CAO等[3]提出基于时变交通流的多模糊时间窗车辆路径问题。多目标VRP(Multi-objective Vehicle Routing Problem,MOVRP)问题[4]根据现实情况构建多个目标,能更好满足配送中心或客户的需求。例如,仅以路径最短为目标,在遇到交通拥堵时,最短路径会成为耗时最长的路径[5]。因此,除了考虑最短路径,还需考虑运输时间、客户满意度、路径均衡度、环境保护等因素。学者们考虑较多的是双目标车辆路径问题,如同时考虑最小配送成本和最大客户满意度,运输成本和路径间的平衡[6-7]。在双目标的基础上,WANG等[8]研究行驶路程最短、行驶时间最小、等待时间最短、车辆数最少和客户满意度最大5个目标问题。随着生活水平的不断提高,多目标VRP会更加丰富。VRP属于NP-hard问题,目前较多采用智能算法进行求解[9],如禁忌搜索算法和遗传算法。多目标VRP由于目标之间的不可比较性,较多学者采用化多目标为单目标进行解的优劣性判断。蚁群算法是一种模拟进化算法,具有许多优良的性质,在车辆路径问题中得到广泛的应用[10-11]。基于以上研究,本文以线路里程最短和线路均衡度最好为双目标,考虑随机需求的影响性,建立带硬时间窗约束的双目标车辆路径规划模型(Multi-objective Vehicle Routing Problem with Hard Time Windows,MOVRPHTW)。采用非支配排序策略选择迭代后的精英蚁群释放信息素,获得货物配送方案的Pareto最优车辆路径解集,以供配送中心参考。
1 问题描述与模型建立
1.1 问题描述
客户需求量受到多种因素的影响,会出现一定的波动性。当以期望固定客户需求,规划配送路径方案时,若客户需求量小,则浪费车辆运力;当客户需求量大,则部分客户需求无法得到满足,需再派车进行二次服务,进而增加车辆配送成本。考虑需求的随机波动性,本文研究的MOVRPHTW问题,可以描述为:在一个产品配送中心,有一列车辆数为m的车队装载货物从配送中心出发,向一组位置、服务时间、需求量期望和方差已知的n个客户分发货物,分发完货物后返回配送中心,寻找一个配送方案,使配送方案线路里程最短和线路均衡度最好。
1.2 模型假设及符号说明
基本假设:
1)客户点位置、服务时间、时间窗已知,由一辆车进行配送;
2)客户需求不确定,满足相互独立的随机分布,其中客户需求期望uj和方差σj已知;
3)配送中心位置,出发时间、返回时间已知;
4)客户在规定时间窗内接受服务,车辆早到等待到ei时接受服务,不允许晚到;
5)客户之间及配送中心和客户之间的行驶距离固定,距离满足三角不等式;

6)车辆从配送中心出发,完成配送任务后,在规定时间前返回配送中心。
假设运输网络[12]G=(V,A),模型参数及相关变量如表1所示。

表1 模型参数及变量Table 1 Model parameters and variables
1.3 考虑随机需求的运输可靠性分析
客户点的需求是随机满足一定分布,车辆ξk所服务的运输量如式(2)。

配送中心根据实际运营情况给定一个可靠性概率θ,车辆k的运载能力满足可靠性约束式(3),即车辆所服务客户的货物需求总量的概率大于可靠性所要求的概率。

对于式(2),客户点j的货物需求量服从期望μj,方差σ2j已知的分布。根据大数定律[13-14],车辆运输需求总量服从ξk~N(μk,σk)的正态分布,其中车辆运载期望μk和方差σ2k,如式(4)~(5)所示。

(ξk-μk)/σk服从标准正态分布,如式(6)所示,其中ϕk通过给定的θ可查。当车辆限载量满足式(7),则满足式(3),进而可把式(3)转化为式(8),即车辆的限载量W大于期望和方差的额外部分之和。

1.4 多目标车辆路径优化模型
目标函数:
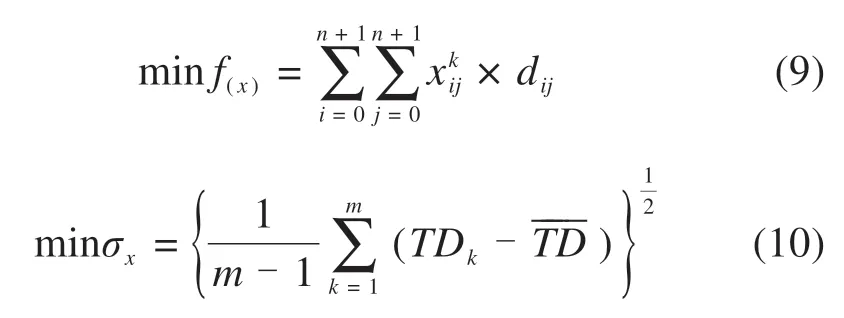
约束条件:
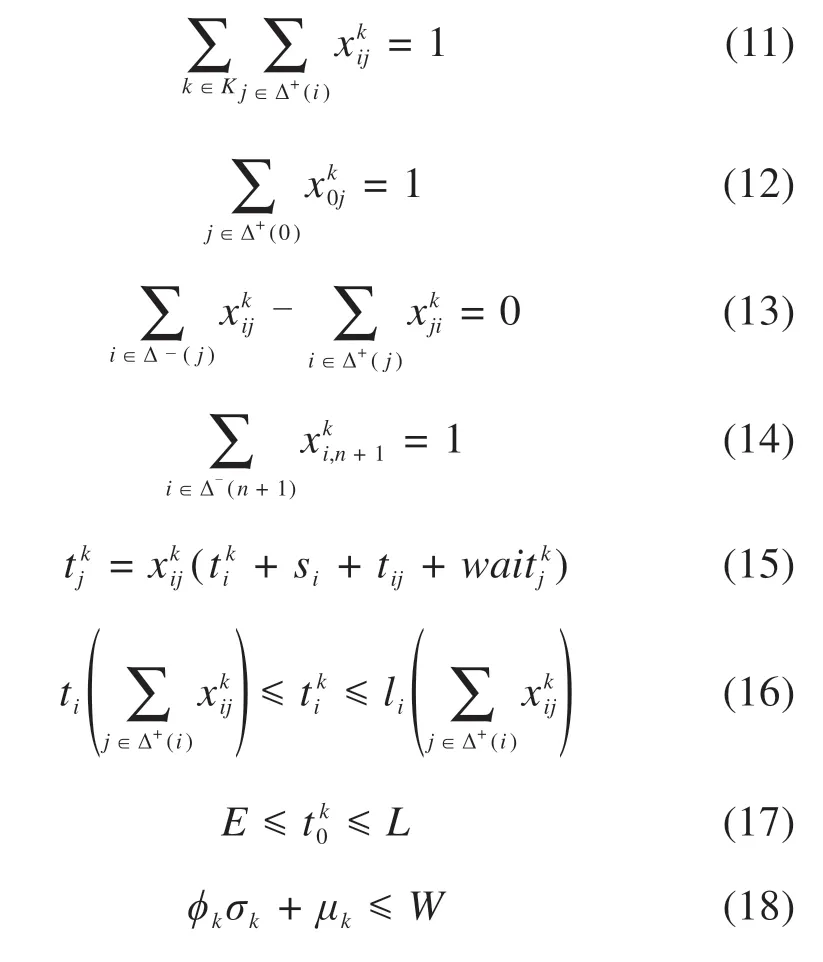
式(9)和式(10)是MOVRPHTW的目标函数,目标(9)是各线路长度之和,即线路里程,目标(10)是各线路长度方差,即线路均衡度。式(11)表示1个客户只能由1辆车服务。式(12)~(14)表示车辆在线路上的流量限制。式(16)~(17)是硬时间窗限制,式(18)是随机需求下的运输量限制约束。
2 快速非支配排序的精英蚁群算法
2.1 配送路径编码和解码
根据MOVRPHTW特点,设计以车辆为单位,依次对需要服务的客户进行编码,构造行车路径。假设n=10,客户编号为{1,2,3,4,5,6,7,8,9,10},需要服务的客户产品需求量为{2,3,1,1,2,2,1,1,1,2},配送中心的车辆编号为{11,12,13},1个可行车辆路径的编码及解码,如图1所示。

图1 编码与解码Fig.1 Encoding and decoding
路径编码序列为:以车辆编号开头并包含客户编号的一组数据序列;解码序列为:车辆11依次服务客户1,6,9,运载量为 5;车辆12依次服务客户3,7,2,运载量为 5;车辆13依次服务客户8,10,5,4,运载量为6。
2.2 蚂蚁状态转移概率
在蚂蚁状态概率转移公式中,考虑信息素、路径距离启发函数、时间窗宽度及蚂蚁等待时间对蚂蚁转移概率的影响,如式(19):
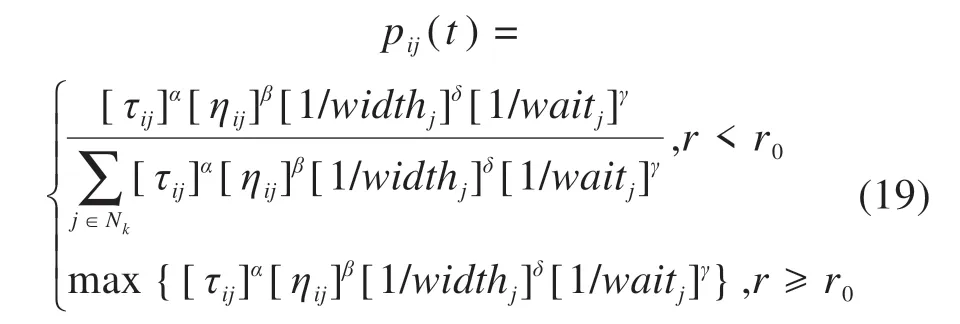
其中:τij是信息素启发因子,ηij=是距离启发因子,widthj=lj-ej是客户的时间窗宽度因子,r0=0.5转移规则参数,waitj=max{(ej-tjk),0}是客户的等待时间,α,β,δ,γ是其参数重要程度因子。
2.3 基于贪心算法的种群初始化策略
蚁群算法采用随机方式生成初始蚁群对求解结果影响较小,但相关研究表明:虽然非随机方式生成的初始可行解会缺乏多样性,但其有可能产生高质量的最优近似解。本文对双目标函数进行归一化处理,即贪心目标:

采用贪心算法和随机方式构建蚂蚁初始蚁群,初始化策略步骤如下所示。
步骤1:车辆随机访问第1个服务的客户点。
步骤2:再访问下一点时,分别把未访问客户点加入路径中。如果车辆不满足运载可靠性约束,则车辆返回配送中心,开始下一条配送;如果车辆满足运载可靠性约束,若车辆早到达客户,则等待后继续服务,若车辆晚到,开始下一条配送,即运输路径必须满足客户硬时间窗约束。车辆能继续访问的客户点即为待访问客户集合,从待访问客户集合中,采用如下伪代码访问客户点:

注:其pi用于增加初始解的多样性。
2.4 邻域搜索操作
VRP随着客户点的增多,解空间规模呈指数级增加,单一的蚁群迭代很难搜索到较满意解,为增加局部搜索能力,本文从配送方案的线路设计2种邻域搜索(Neighborhood Search,NS)操作[15]:
1)路径内破坏与修复操作:线路内随机选择一个客户点进行破坏与修复操作,若修复后的线路不满足约束条件,则从不满足的客户点进行拆分,直到满足约束条件为止,客户3的破坏与修复,如图2所示。

图2 路径破坏与修复Fig.2 Route damage and repair
2)路径间的交换操作:从不同的2条线路随机选2个客户点进行线路间的交换操作。改变线路的不可行性时,进行线路拆分,直到满足约束条件为止,交换操作如图3所示。
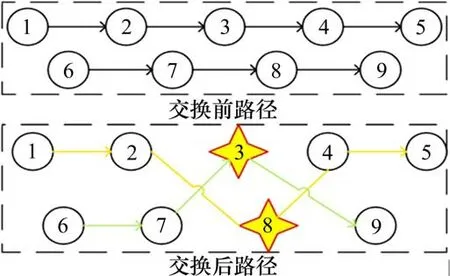
图3 路径交换Fig.3 Route switching
为避免邻域操作中,线路拆分带来的车辆数增加,把拆分后最短线路客户依次从前往后加入到配送方案中其他线路最短客户中,直到拆分最短线路客户点全部分配完为止。若存在拆分最短线路客户点都不满足约束条件,则此次邻域搜索操作失败。这样既能避免车辆数增加也能提高车辆运载效率。
2.5 非支配排序的精英蚂蚁选择策略
在线路里程和均衡度的解空间{f(x),σ(x)}中,解集之间存在着2种情况[16]:
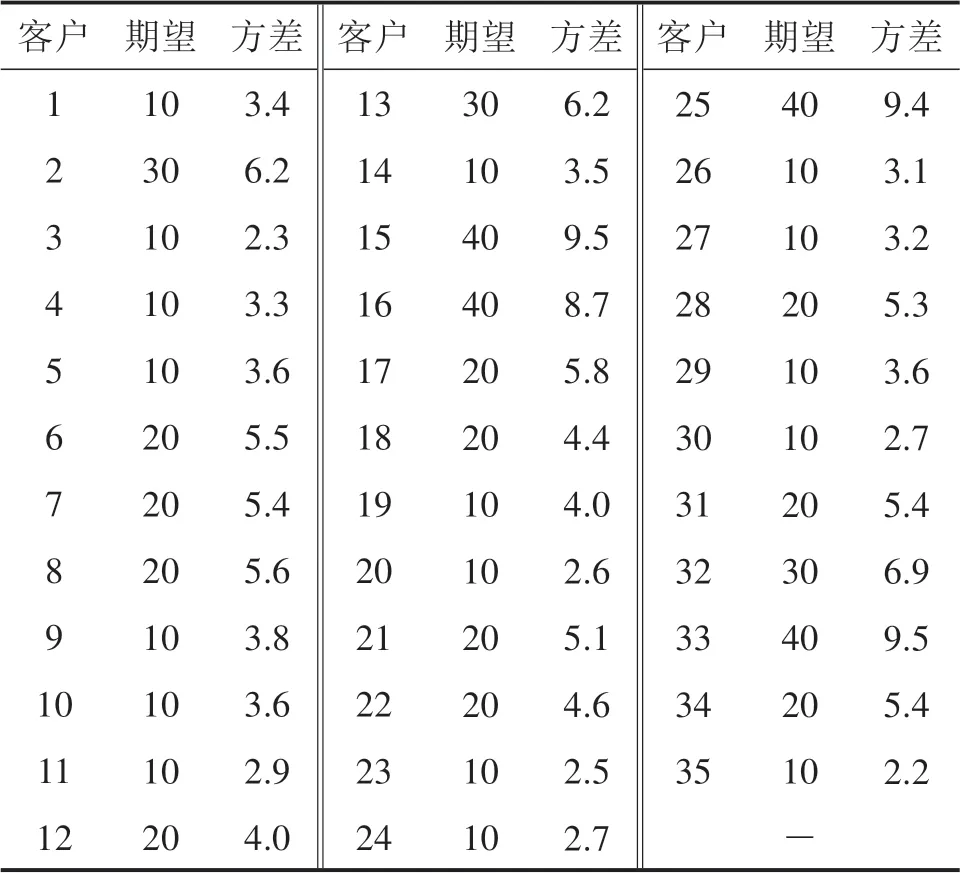
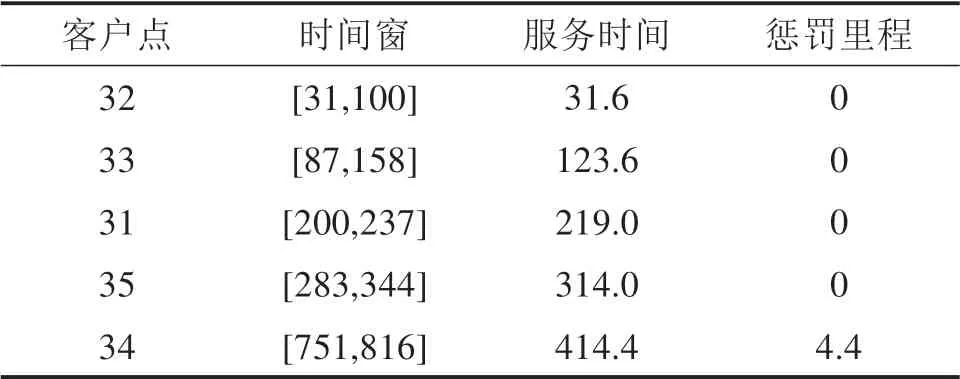
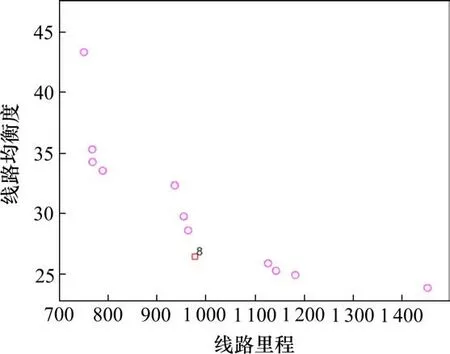
当f1(x) 当f1(x) 在线路里程和线路均衡度双目标车辆路径问题中,通常存在第2种情况的解集,其对应目标空间中的目标矢量所构成的曲线称作Pareto最优前沿[17-18]。本文设计的精英蚂蚁信息素释放策略如下所示: 1)快速非支配排序算子 在Pareto最优解集中依据个体非劣解水平对蚁群分层,指引蚂蚁向最优解集方向搜索[19]。这是一个循环适应分级过程:1)找出群体中非支配解集,记为第1个非支配层,赋予非支配序irank=1,并从蚁群中去除;2)继续寻找余下蚁群中非支配解集,记为第2个非支配层,赋予非支配序irank= 2;3)继续循环,直到整个蚁群被分层,同一层内非支配序irank相等。 2)蚂蚁拥挤距离算子 为了对同一非支配层内的蚂蚁个体进行选择性排序,引入拥挤度概念。计算步骤如下: 步骤1:蚂蚁初始化距离,L[i]d=0。 步骤2:非支配层排序。同一非支配层个体按目标函数值升序排列。 步骤3:蚂蚁个体边缘选择优势。给定一个大数M,令L[1]d=L[end]d=M。 步骤4:根据式(21)计算拥挤距离。 步骤5:对线路里程和均衡度的拥挤距离求和,得到个体拥挤度进行降序排列。 其中L[i+1]g表示第i+1个蚂蚁的第g个目标函数值。fmaxg,fming分别为蚁群中第g个目标函数的最大值和最小值。 分别对线路里程和均衡度重复步骤2~4,得到蚂蚁i的拥挤度L[i],优先选择非支配层靠前,拥挤度较大的蚂蚁,以维持蚂蚁种群多样性。 3)精英蚂蚁选择算子 精英蚂蚁选择策略即保留蚁群中的优良个体进行信息素释放,以防止Pareto最优解的丢失。按照非支配排序irank从低到高排序,拥挤度从大到小排序,选择一定数量的蚂蚁种群进行信息素释放[20]。蚂蚁k的信息素释策略如式(22)~(23): 其中:ρ是信息素蒸发系数;Q是信息素总量。 设计基于非支配排序的精英蚁群算法求解MOVRPHTW问题,核心思想有4个部分:种群初始化、概率转移公式、局部邻域搜索、信息素更新。在每次蚁群迭代结束后,依据2.5节选择前25只蚂蚁释放信息素,算法流程如图4所示。 图4 非支配排序的精英蚁群算法Fig.4 Elite ant colony algorithm for non-dominated sorting 实验在同一环境中进行,其中CPU主频为2.30 GHz,内存32 G,操作系统为64位Windows7,编程语言为MATLAB R2018,以Solomon中C1类部分客户进行仿真实验。 为更好体现不同需求和时间窗带来的路径差异性,以式(9)线路里程为目标,选取C101类前35个客户,以固定需求为随机需求期望,根据需求量随机产生不同范围方差,此算例中客户点期望和方差如表2所示,算法的相关参数如表3所示,θ对应的ϕk=1.28。在考虑不同需求和时间窗情况下建立3种情形,如表4所示,其中软时间窗无论何时到达都接受服务,采用式(24)增加时间惩罚里程,车辆k从i到j的惩罚里程为: 表2 客户点期望和方差Table 2 Customer point expectations and variance 表3 算法参数水平Table 3 Combination of ACO parameter values 表4 不同情形下的约束条件Table 4 Constraints in different situations 3种情形下的配送路径和运载量如表5所示,配送方案路线图如图5所示。鉴于文章篇幅所限,只列出情形2下线路5的服务时间及里程惩罚值,如表6所示。情形3下线路5的到达时间和等待时间,如表7所示。 表6 情形2下线路5服务时间及惩罚里程Table 6 Line 5 service time and penalty mileage of scenario 2 表7 情形3下线路5到达时间及等待时间Table 7 Line 5 arrival time and waiting time of scenario 3 图5 3种情形下配送方案Fig.5 Route map of the distribution plan in three scenarios 表5 不同情形下配送路径Table 5 Distribution route under fixed demand and stochastic demand 在硬时间窗下,当考虑固定需求和随机需求时,即情形1和情形3。如情形1中,4条配送路径都满足固定需求时的车辆运载能力,但在随机需求下,路径1,路径2和路径3都不满足运载可靠性约束,即配送路径方案不可行;情形3中,5条路径都满足运载可靠性约束。情形3和情形1相比,线路里程增加127.49,因此,配送企业应考虑需求的随机性对线路里程的增加程度。 在随机需求下,当考虑时间惩罚里程和硬时间窗时,即情形2和情形3。如情形2中的线路5,车辆到达客户点后即开始服务,但由于服务客户点34时,在接受时间外到达产生值为4.4的线路惩罚里程;情形3中,线路5服务客户点30时,车辆早到,那么等待时间为19.9,在到客户点30左时间窗时开始接受服务。 为分析设计算法参数对Pareto解的分布产生影响,取C101类前50个客户,设置蚂蚁数量为100,迭代200次,进行多次实验,分析参数对Pareto解质量的影响。 由图6可知,总体上随着权重因子的增大,解的质量变好,但因子权重过大,解的质量和多样性变差。 图6 蚁群参数α,β,γ,δ灵敏度分析Fig.6 Sensitivity analysis α,β,γ,δ of ant colony parameters 1)参数α。随着参数α的增大,解的质量较好,原因是由于精英蚂蚁对解的指引性较强。 2)参数β。当β=3时,解的质量变差,可能是由于里程启发因子权重过大,导致在路径选择中忽略了线路均衡度,具体原因有待进一步研究。 3)对于参数δ。当δ=3时,解的质量、多样性、分布性变差,可能是由于时间窗宽度因子权重过大,蚂蚁优先服务时间紧迫性高的客户,这类分析有助于研究客户时间紧迫性对配送路程的影响。 4)对于参数γ。当γ=3时,解的质量最差,可能是由于等待时间因子权重过大,导致蚂蚁过度等待。 由图7可知,对于信息素挥发因子ρ,当ρ较小时解的质量较好,可能是由于此类客户地理位置分布较为集中,路径选择方案较多。 根据3.1节和3.2节,设置非支配排序蚁群算法相关参数,求解最后一次迭代的第1层非支配Pareto解集,如表8所示Pareto解曲线如图8所示,Pareto解8的配送路径方案如图9所示,以供配送中心根据实际情况合理选择配送路径方案。 表8 C101类客户Pareto解值Table 8 Class C101 customer Pareto solutions values 图8 C101类客户Pareto解Fig.8 Class C101 customer Pareto solutions 1)从配送中心的角度出发,配送费用不仅与行驶里程有关,还可能与线路均衡度有关,构建双目标车辆路径问题:以线路里程最短和线路均衡度最好为目标函数,考虑车辆运输可靠性约束,建立带硬时间窗的车辆路径模型,并设计基于非支配排序的精英蚁群算法进行求解。 2)用Solomon中的C101算例,以运输可靠性考虑不同随机需求、硬时间窗约束的影响,可以发现随机需求和硬时间窗虽然带来线路里程的增加,但运输更加可靠。因此配送企业应结合客户的配送特点,如服务时间的优先级等,合理安排配送路径。 3)根据蚁群算法参数的灵敏度进行分析,合理设置蚁群参数,求C101类客户配送方案的Pareto解,可以发现不同非支配解的线路均衡度变化不大,但线路里程和车辆数差别较大,配送企业应结合路径均衡度对司机薪酬和车辆状况的影响程度以及市场对产品需求的波动情况合理安排配送路径。
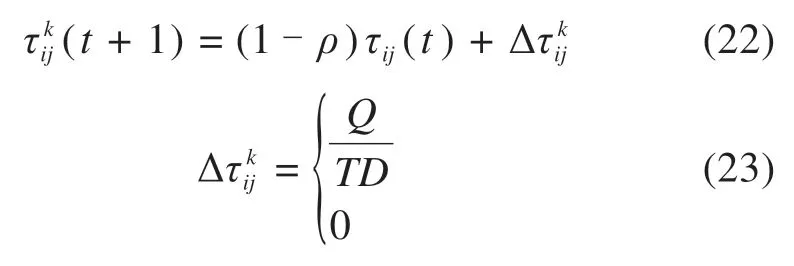
2.6 算法步骤
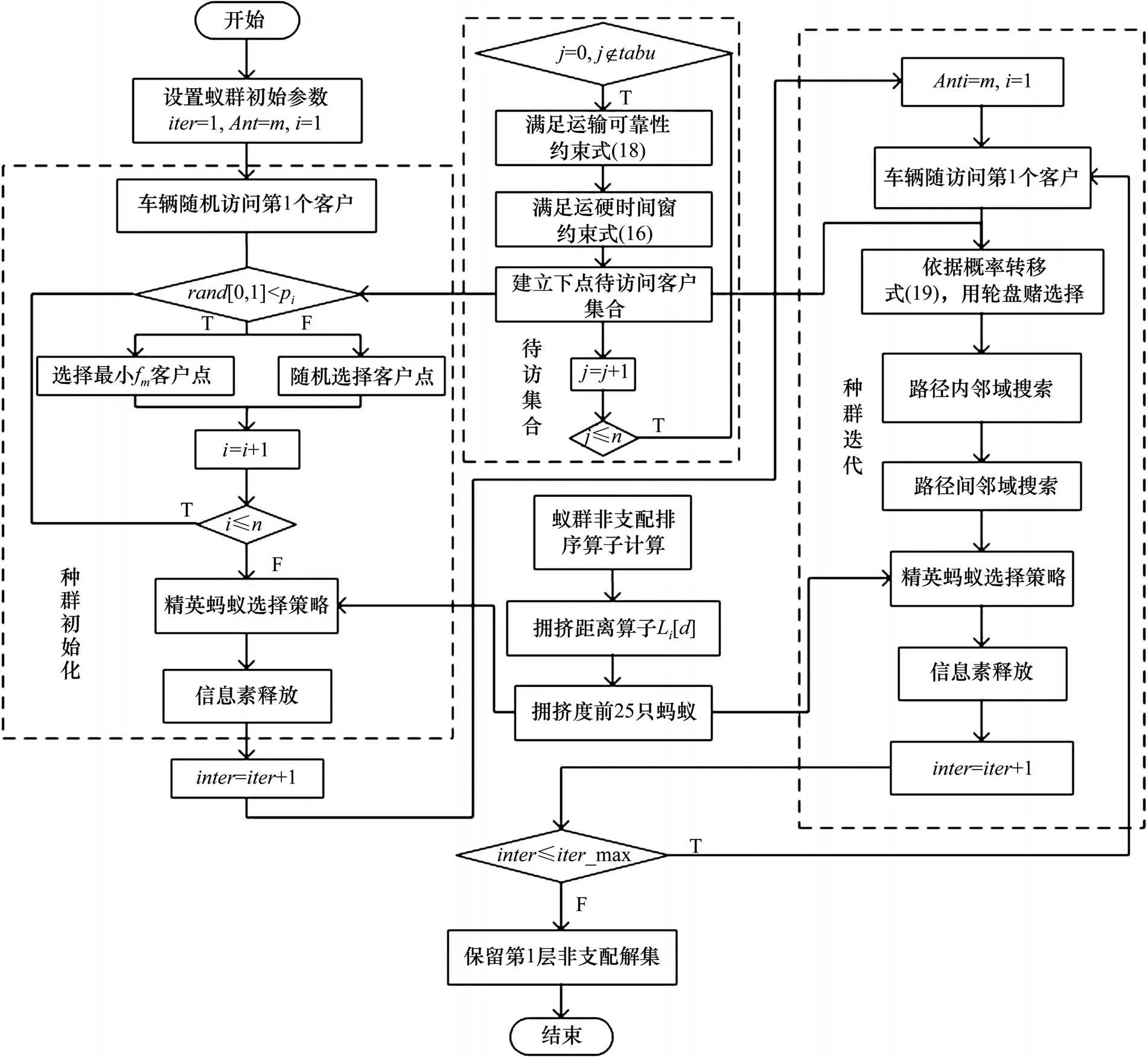
3 算例仿真实验
3.1 随机需求和时间窗影响分析






3.2 参数灵敏度分析

3.3 双目标算例分析

4 结论
