海洋平台导管架Y形节点焊接冷裂性评价

冯超，赵雷，徐连勇，韩永典，郭慧娟

(1.天津大学，天津 300350；2.天津市现代连接技术重点实验室，天津 300350)

0 前言

随着世界陆地化石能源的日趋减少，海洋化石能源的开发日益成为各国家大力发展的重点[1-2]。海洋深水平台的性能是海洋化石能源开发中的关键环节，特别是海洋平台的服役寿命与安全性能与海洋平台的复杂结构与焊接技术息息相关[3-5]。由于结构的不均匀性及焊接技术的固有特点，海洋平台导管架节点位置存在应力集中，易导致焊接冷裂纹的产生，进一步影响到海洋平台结构的服役寿命与安全性能[6-8]。

当前随着科学技术的进步，海洋平台结构越来越趋于大型化，仅依靠试验手段难以进行大量、准确的研究，因此定量评价海洋平台导管架Y形节点焊接冷裂性具有重要的现实意义。随着有限元技术的不断发展和应用，不同过渡性网格的使用可以满足不同场函数的需要，并通过软件的后处理功能简化了焊接过程的有限元分析[9-11]。苗文成[12]通过大量实际海洋平台导管架结构管节点的实际焊接试验，发现焊接过程中进行合理的预热与后热并尽量降低焊条中氢的存在，有利于抑制导管架结构管节点裂纹的产生。吴海涛等人[13]利用三维分析软件对海洋平台桩腿的裂纹扩展行为进行了有限元分析分析，通过应力强度因子的合理计算及扭转载荷与压力载荷的合理使用实现了实际服役情况的有效模拟，获得了准确的模拟结果。陈哲等人[14]基于试验手段对不同焊接方法条件下的焊接接头的疲劳裂纹扩展速率进行了研究，发现使用焊条电弧焊打底、药芯焊丝焊填充并盖面的焊接方法具有较好的疲劳性能。陈飞宇等人[15]基于疲劳裂纹的相关理论，通过考虑海洋平台导管架结构的实际服役环境计算热点应力，进而通过疲劳裂纹扩展行为的分析对导管架结构的疲劳寿命与可靠性进行了评定，有利于海洋平台的服役安全性。

综上所述，随着目前海洋平台越来越趋于大型化，文中基于RRC试验机理，利用数值模拟方法对导管架Y形管节点的拘束应力进行分析，进而定量评价其冷裂性，从而为海洋平台结构的安全服役提供借鉴意义。

1 数值模型建立

采用SYSWELD软件对海洋平台导管架Y形管节点焊缝进行建模并进行焊接过程模拟，根据焊后应力场获得焊后拘束应力，从而实现对其冷裂性的定量评价。

1.1 计算区域

选取导管架结构的Y形节点进行建模计算，其实际焊接过程与坡口形状如图1、图2所示。导管架结构中，支管被主管截取的断面称为马鞍形坡口，填充的焊缝为马鞍形焊缝。

图1 实际焊接过程

图2 实际坡口形状

为合理评价导管架Y形管节点的冷裂性，依据以下步骤建立马鞍形焊缝的计算区域：①利用CAD软件，根据如图3所示样板图完成马鞍形坡口相贯线和坡口线的绘制，其中相贯线与坡口线在支管圆周上分别有36个样点；②利用UG软件，以一定角度做出支管的中心轴线，用阵列法分别做出与中心轴线平行并将投射圆均分为36份的一系列基准线；③以投射图为基准面，坐标轴线为基准线，根据相贯线与坡口线的坐标，连接后分别得到管节点的相贯线与坡口线；④根据坡口线进行拉伸得到支管模型和马鞍形坡口进行焊缝填充，得到马鞍形焊缝的三维模型，如图4所示。

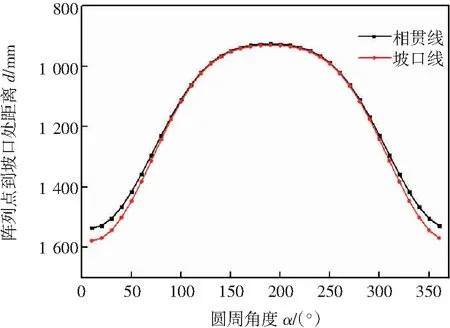
图3 马鞍形坡口样板图

图4 马鞍形坡口及焊缝填充图

基于所建三维实体模型，在满足精度的前提下，提高计算效率，减小存储空间。为节省计算时间，基于模型的对称性，采取1/2模型进行计算。导管架Y形节点及相应的马鞍形焊缝的三维网格模型分别如图5、图6所示。其中，模型与实际结构尺寸比例为1∶1，网格总数约为82万。

图5 Y形管节点网格划分

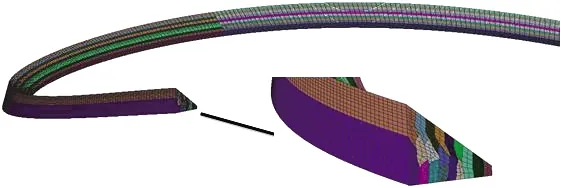
图6 焊缝区网格划分

1.2 材料性能

文中所使用的材料为海洋平台导管架专用钢E36高强钢，其名义化学成分见表1。利用感应加热设备对坡口预热至66 ℃并保温60 s，焊丝牌号为GFL-71Ni，采用FCAW-G工艺进行焊接，热输入为1.1 kJ/mm。

表1 E36钢化学成分(质量分数，%)

在数值模拟过程中，E36高强钢随温度变化的热物理性能、力学性能参数及不同温度下的应力应变曲线如图7所示[16]。焊接过程的数值模拟过程采用等强匹配原理，即焊缝和母材均采用同一E36高强钢材料的性能参数。

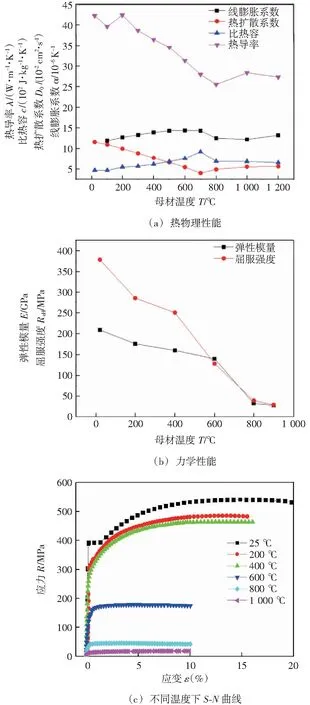
图7 E36高强钢性能参数

1.3 边界条件

文中通过热源校核得到的热循环曲线实现热源模型的施加，其步骤为：①建立局部三维有限元模型，为不影响散热，实现对焊接过程的合理模拟，得到较为准确的温度场，模型的大小以焊接温度场达到准稳态时所能达到的最远距离为边界；②数值模拟过程中，由温度超过材料熔点的单元围成焊缝轮廓，将其与实际焊缝形状进行对比分析直至模拟结果验证良好；③对节点处焊缝的热循环曲线进行提取，取平均值后导出数据如图8所示，并写入热源函数。

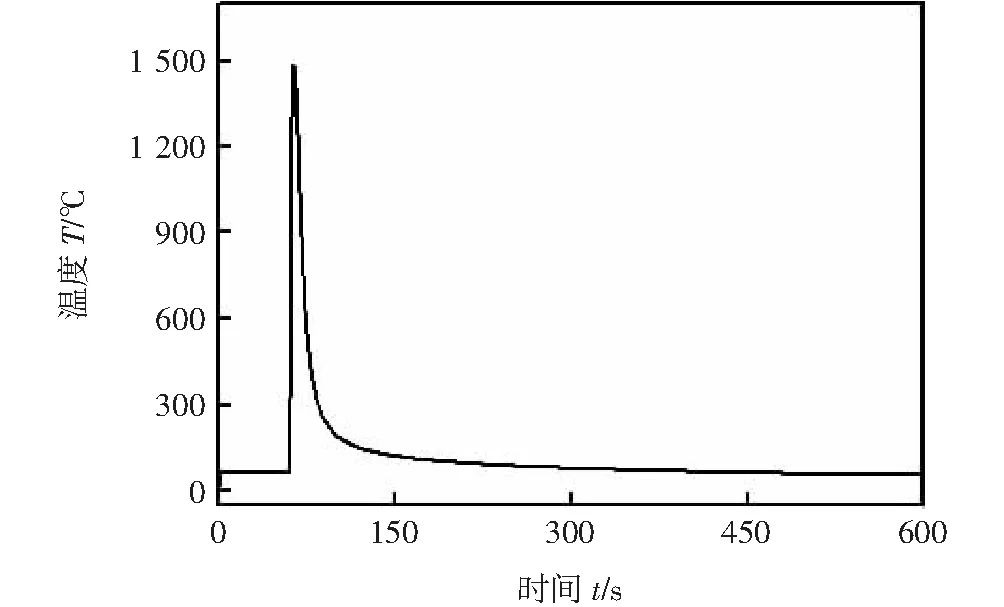
图8 热循环曲线

在数值模拟过程中，不同的夹持条件所产生的拘束状态有所不同，焊接过程中夹持条件会导致拘束应力的产生，从而影响最终的拘束应力分布。在数值模拟过程中，约束的施加原则是不能限制焊接过程中的应力释放和自由变形，也不能产生刚性位移。根据实际焊接过程中Y形管节点的拘束状态来确定数值模拟过程中的夹持条件，这是得到准确数值模拟结果的重要前提。如图9所示为根据实际拘束条件得到的夹持情况，在焊接过程中认为Y形管节点为全约束状态。

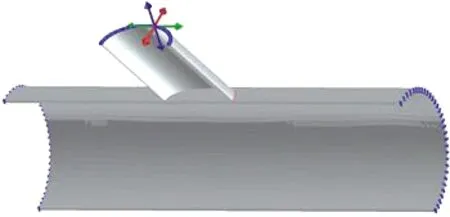
图9 Y形接头的夹持条件

2 管内壁冷裂性评价

图10为焊接完成后所建三维数值模型的拘束应力云图，展示了焊缝不同区域的等效应力。Y形管节点由于其结构的特殊性存在较大的应力集中，容易成为焊接延迟裂纹的起裂位置。在以支管为基准的柱坐标系下，提取管内壁焊根处沿着内相贯线的应力分布和管外壁焊趾处沿着外相贯线的应力分布(方向为顺时针)，从而对拘束应力进行分析并对冷裂性进行定量评价。

图10 拘束应力云图

如图11所示，管内壁焊根处轴向拘束应力以拉应力为主，仅在距离起始位置0～200 mm范围拘束应力呈现出较小的压应力；随着距离的增大，轴向拘束应力不断上升，在距离起始位置650 mm处达到第一个应力峰值263 MPa；距离起始位置650 mm到1 270 mm范围内，轴向拘束应力先降低后升高；在距离起始位置1 270 mm处拘束应力峰值达到第二个峰值306 MPa；之后随着距离的增加，拘束应力逐渐降低。管内壁轴向拘束应力的两个峰值代表了这两处为容易发生焊接冷裂纹的危险点，与前期基于RRC试验法得到的材料的临界拘束应力625.1 MPa[16-17]相比，管内壁危险点的轴向拘束应力值小于材料的临界拘束应力，即σ轴<σcr。即如果以管内壁焊根处的轴向拘束应力大小为判据，则数值模拟得到的拘束应力小于材料的临界拘束应力，结构不会发生开裂。

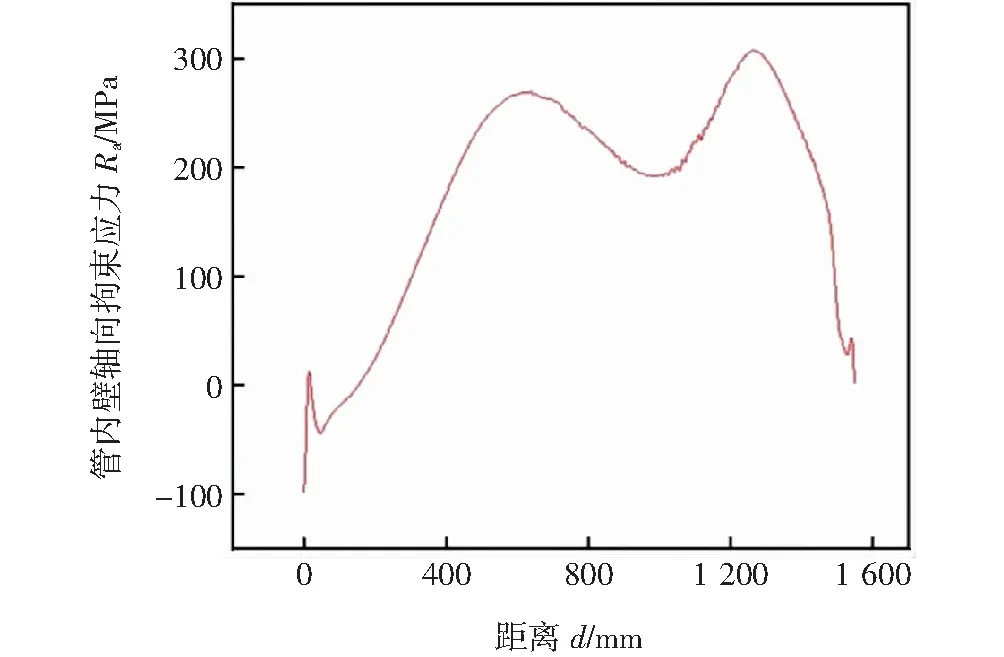
图11 管内壁焊根处轴向拘束应力

如图12所示，管内壁焊根处周向拘束应力几乎全部为拉应力，在起始距离起始位置0～35 mm范围内的应力波动后，拘束应力随着距离的增大不断上升，在距离起始位置105 mm处达到第一个应力峰值312 MPa；随着距离的不断增加，拘束应力逐渐降低并在马鞍形焊缝的中间位置达到最低值，约为0 MPa；随着距离的继续增加，应力急剧上升，在距离起始位置1 500 mm处达到第二个峰值481 MPa；之后随着距离的增加，拘束应力逐渐降低。与管内壁轴向拘束应力相同，周向拘束应力的2个峰值代表了这两处为焊接冷裂纹容易发生的危险点，与材料的临界拘束应力625.1 MPa相比，管内壁危险点的周向拘束应力值小于材料的临界拘束应力，即σ周<σcr。即如果以管内壁焊根处的周向拘束应力大小为判据，则数值模拟得到的拘束应力小于材料的临界拘束应力，结构不会发生开裂。

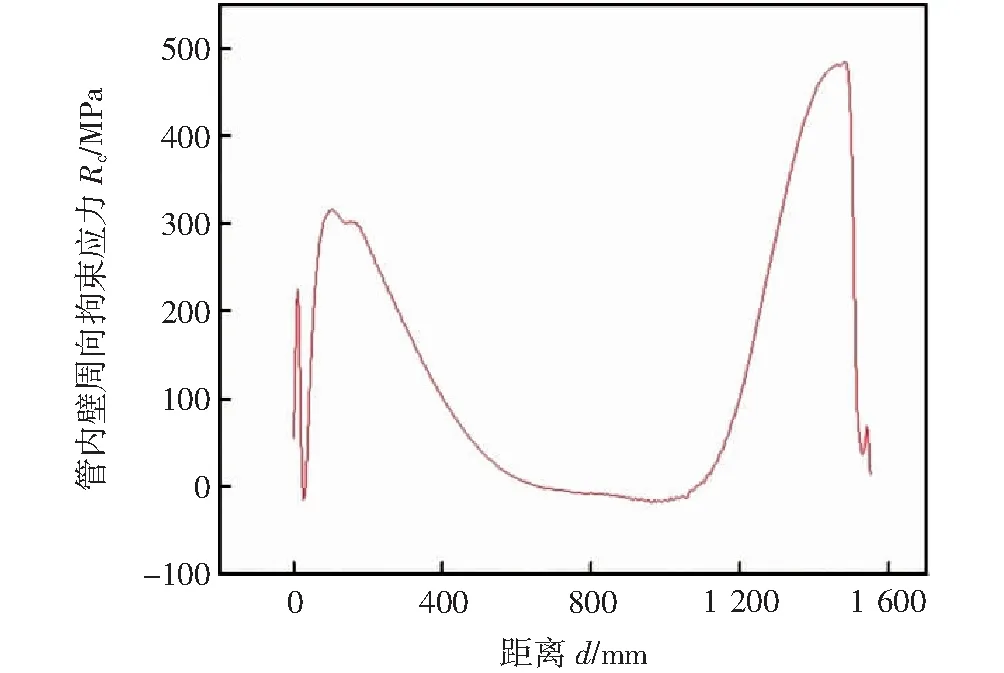
图12 管内壁焊根处周向拘束应力

如图13所示，管内壁焊根处径向拘束应力以压应力为主，距离起始位置0～10 mm范围内，径向拘束应力由-220 MPa 陡升至79 MPa，即由较大的压应力转变为拉应力；随着距离增大，拉应力又逐渐转变为压应力，且压应力在距离起始位置891 mm位置处达到峰值321 MPa；随着距离继续增大，压应力逐渐减小，并在距离起始位置1 210 mm处压应力减小为零，拉应力逐渐升高；在距离起始位置1 489 mm处拉应力达到峰值492 MPa。与内壁焊根处的轴向和周向拘束应力不同，管内壁焊根处径向拘束应力以压应力为主，且仅在距离起始位置1 489 mm处存在一个拉应力峰值，该处为焊接冷裂纹容易发生的危险点，与材料的临界拘束应力625.1 MPa相比，管内壁危险点的径向拘束应力值小于材料的临界拘束应力，即σ径<σcr。即如果以管内壁焊根处的径向拘束应力大小为判据，则数值模拟得到的拘束应力小于材料的临界拘束应力，结构不会发生开裂。

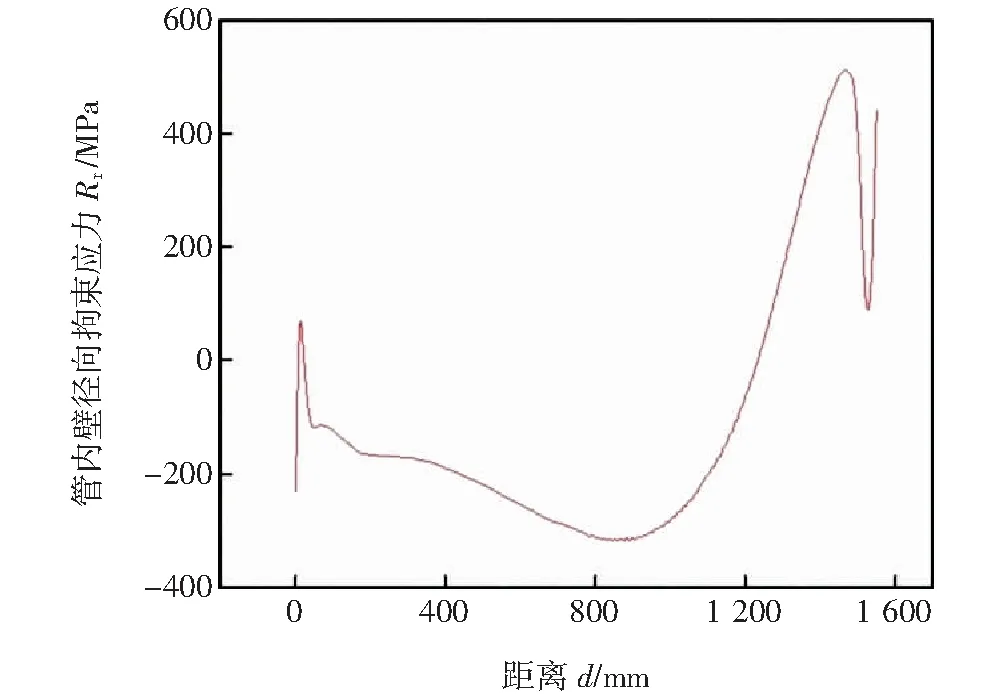
图13 管内壁焊根处径向拘束应力

3 管外壁冷裂性评价

如图14所示，管外壁焊趾处轴向拘束应力规律性较强，呈现出近似的对称分布。距离起始位置0～800 mm范围内，拘束应力由-215 MPa上升到389 MPa，即压应力由215 MPa逐渐减小至零，拉应力由零逐渐上升到389 MPa；在距离起始位置800～1 600 mm范围内，拘束应力的变化与前一段恰好相反，拉应力由峰值逐渐减小，减小到零后，压应力逐渐增加。因此距离起始位置800 mm附近区域为焊接冷裂纹容易发生的危险点，与材料的临界拘束应力625.1 MPa相比，管外壁危险点的轴向拘束应力值小于材料的临界拘束应力，即σ轴<σcr。即如果以管外壁焊趾处的轴向拘束应力大小为判据，则数值模拟得到的拘束应力小于材料的临界拘束应力，结构不会发生开裂。

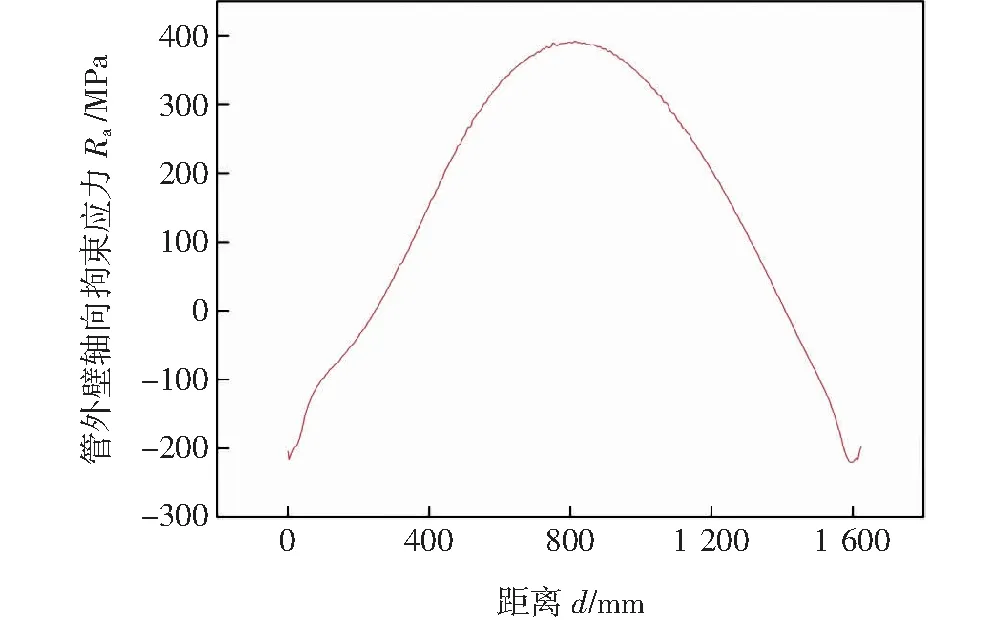
图14 管外壁焊趾处轴向拘束应力

如图15所示，管外壁焊趾处周向拘束应力分布与轴向拘束应力相似，也呈现出近似的对称分布。根据拘束应力分布情况，在提取路线的起始段和终止端的小范围内，拘束应力都有一个跳跃式波动，但均为压应力。在其余位置，拘束应力均为拉应力，在距离起始位置80 mm到150 mm范围内，拘束应力由0 MPa增加到271 MPa；随着距离继续增加，拘束应力在距离起始位置800 mm位置处拉应力降低为0 MPa；随后逐渐增加并在距离起始位置1 510 mm位置达到第二个拘束应力峰值，102 MPa。周向拘束应力的两个峰值代表了这两处为焊接冷裂纹容易发生的危险点，与材料的临界拘束应力625.1 MPa相比，管外壁危险点的周向拘束应力值小于材料的临界拘束应力，即σ周<σcr。即以管外壁焊趾处的周向拘束应力大小为判据，则数值模拟得到的拘束应力小于材料的临界拘束应力，结构不会发生开裂。

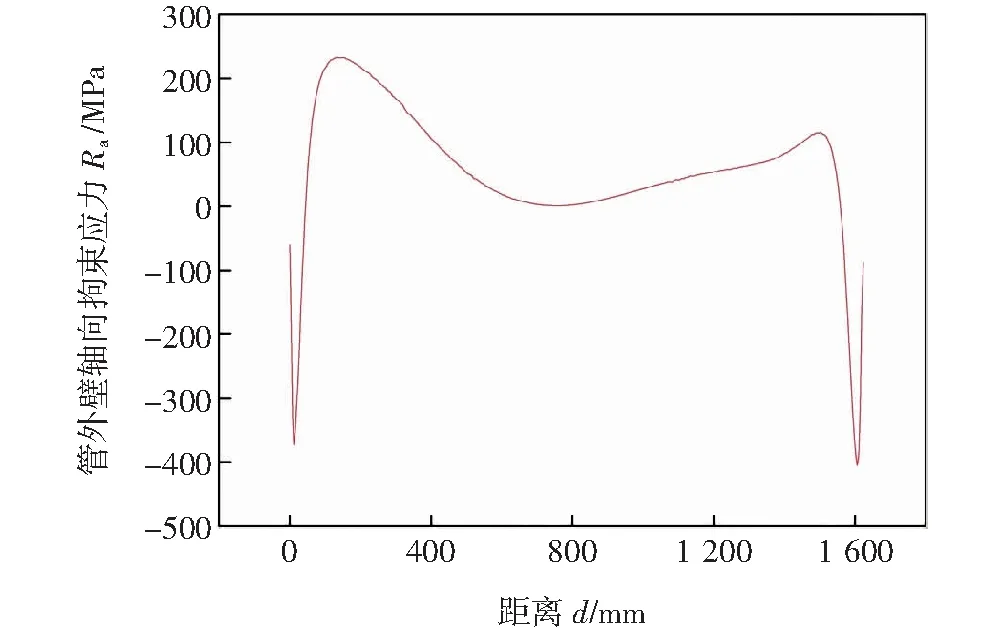
图15 管外壁焊趾处周向拘束应力

如图16所示，管外壁焊趾处径向拘束应力均为压应力，由此可知径向拘束应力对管外壁焊趾的开裂并无促进作用，因此不能采用周向拘束应力大小作为判据来判断管外壁焊趾处是否会发生开裂。

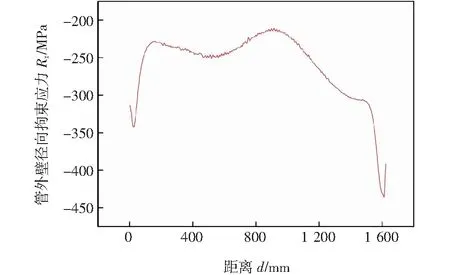
图16 管外壁焊趾处径向拘束应力

4 结论

综上所述，分别对管内壁焊根处和管外壁焊趾处的轴向、周向和径向的拘束应力沿着相贯线的变化进行了分析，并将危险点的拘束应力值与E36高强钢的临界拘束应力进行了对比。分析结果表明，管内壁焊根处和管外壁焊趾处危险点的最大拘束应力值492 MPa小于E36高强钢的临界拘束应力，即导管架Y形管节点的焊根和焊趾处均不会发生焊接延迟开裂。