修正的Poly算子在Orlicz空间内的逼近

王家玮 吴嘎日迪

(1.内蒙古师范大学数学科学学院, 内蒙古 呼和浩特010022;2.内蒙古师范大学应用数学中心, 内蒙古 呼和浩特 010022)

1.引言

文中用M(u)和N(v)表示互余的N函数, 关于N函数的定义及其性质见文[2], 由N函数M(u)生成的Orlicz空间[0,∞)是指具有有限的Orlicz范数

的可测函数的全体{u(x)}, 其中ρ(v,N) =N(v(x))dx是v(x)关于N(v)的模.由文[2]知,Orlicz范数还可由

计算.

关于该算子在Lp空间内的逼近问题已有一些研究, 由于Orlicz空间比Lp空间更“大”, 同时意义也更广泛, 尤其是由不满足Δ2条件的函数生成的Orlicz空间是Lp空间的实质性的扩充,因此本文的结果比文[1]的结果具有更拓展的意义.但目前尚未见到有人在Orlicz空间里研究这类算子的逼近问题.本文借助Hardy-Littlewood极大函数, 凸函数的Jensen不等式以及Orlicz空间中K-泛函与连续模研究了该算子在Orlicz空间内的逼近问题, 给出了逼近阶的估计.

对0,+∞),记

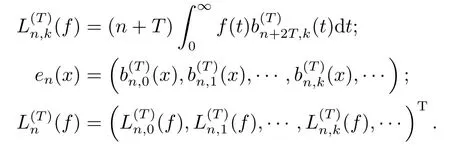
对任意给定的三对角线矩阵

2.相关引理

引理2.1[1]

选适当的ak,bk,ck(k=0,1,···)使之满足

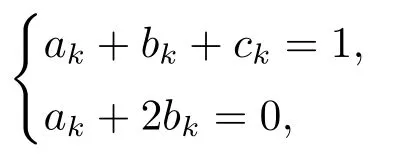
即

在下文中总设{ak},{bk},{ck}为满足(1)式的有界序列,‖f‖M,C表示与f,n,k无关的正常数, 且在不同处可表示不同的值.

引理2.3对每个[0,∞), 有‖Ln(f)‖M ≤‖f‖M.

证

引理2.4对每个[0,∞), 有

证由文[1]中引理2知,

下面证明引理2.5, 引理2.6时用到Orlicz空间中范数计算方法[4−5].

设D为[0,∞)的一稠密子集.

引理2.5对每个g ∈D, 有

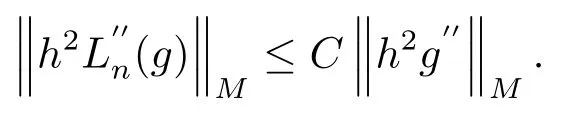
证由于g ∈D, 由文[1]中引理3可知

对∀g ∈D,

由于

由ρ(u,M)≤1, 得知u(t)在[0,∞)上几乎处处有界(见文[4-5]), 于是

则

从而

又

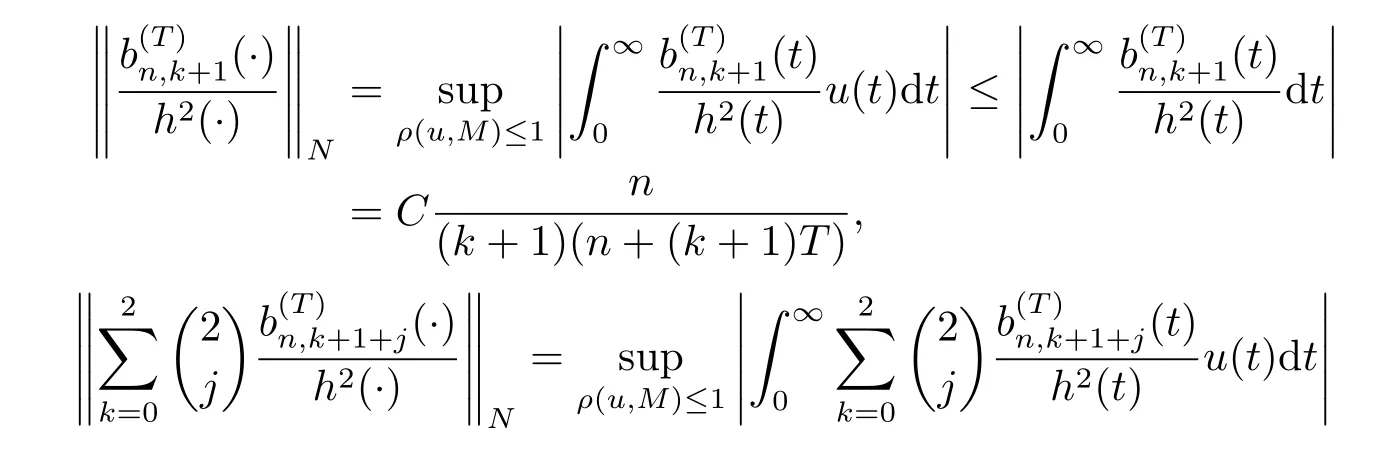
因此

引理2.6对每个g ∈D, 有

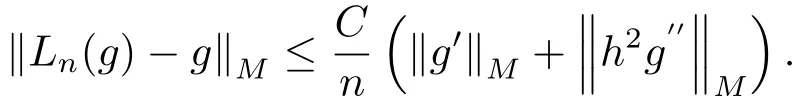
证由Taylor展开

对∀g ∈D, 当x>时, 有

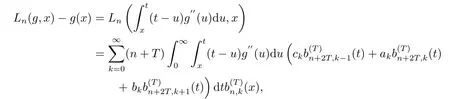
∀x,t ∈[0,∞), 有

u ∈[x,t]或[t,x],

为Hardy-Littlewood极大函数, 且由文[6]中定理2′,‖M(·)‖M ≤‖g‖M, 故

且有

其中ξ ∈[t,x]或[x,t].上述积分的计算结果见文[1]中引理4, 则

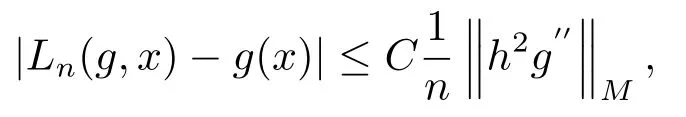
即

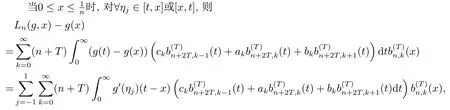
由文[1]中引理4,

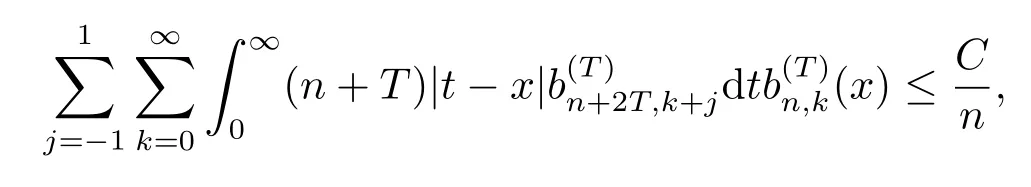
从而

且有

故

从而

综上即得

3.主要结论

设[0,∞),h2(x)=x(1+Tx)(T ≥0), 光滑模中的差分定义为

称

为f的修正光滑模

为f的K-泛函, 则由文[3,7-8]中K-泛函与连续模等价的方法, 得

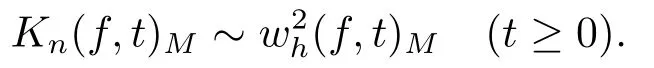
定理3.1设0,∞),h2(x)=x(1+Tx)(T ≥0), 0<α<2, 当n足够大时, 如下命题是等价的.

该定理的证明过程由引理2.3-2.6以及文[8]中第122页的Berens-Lorentz引理可直接得到.