循环冲击载荷作用下滚滑轴承滚子的润滑特性研究*

卢黎明 卢晋夫 李中豪

(1.华东交通大学机电与车辆工程学院 江西南昌 330013;2.江西工业职业技术学院 江西南昌 330099 )

滚滑轴承是一种由圆柱滚子轴承和浮环动压滑动轴承演化而来的新型轴承，它假想将浮环轴承的浮环分割为若干滑块来取代圆柱滚子轴承的保持架，其结构由外圈、内圈、滚子和滑块组成，研究认为该轴承特别适用于在重载低速、间歇运动及频繁启动等工作场合[1-2]。但该轴承是否适合冲击工况，冲击力对其润滑特性影响如何？有待进一步探究。

冲击载荷是一种在极短时间内以极高速度施加在物体上的动载荷，它作用迅速、幅值大。关于其对轴承的影响,JACOBS等[3]通过设计开发了一种新型实验平台，研究了动变载荷对滚滑轴承动态性能的影响[3]；GOVARDHAN等[4]采用谐波动态冲击载荷作用于滚动轴承，得到了轴承滚子在周期载荷作用下的振动规律及载荷特性；RAJE等[5-6]考虑循环冲击下材料的降级，采用离散元法耦合模型计算了滚子损伤疲劳,研究认为冲击载荷对轴承的性能及寿命会产生重要影响。

润滑是改善轴承摩擦副的摩擦状态、降低摩擦阻力、减缓磨损的重要技术措施。关于冲击载荷对润滑油膜的破坏,余谱等人[7]通过建立窄轴承在动载荷作用下的数学模型,分析了冲击载荷作用下窄轴承的润滑性能；GUO等[8]通过研究钢球冲击圆盘过程中的时变弹流润滑问题，得出了油膜厚度随载荷幅值的变化规律。KANETA等[9]研究了不同表面形状滚子在冲击作用下的润滑规律,认为冲击载荷对轴承滚子润滑性能有重要影响。冲击载荷作用下的滚子润滑是一种典型的弹流润滑,对于弹流润滑的研究,早期人们通常将Hertz理论和Reynolds方程结合进行计算;此外还采用直接迭代法、逆解法、牛顿法等进行数值分析,目前采用较多的方法是多重网格法。王鹏等人[10]采用多重网格技术对滚子副急停过程弹流润滑问题进行了数值仿真；杨福芹等[11]采用多重网格法研究了纯滚动工况下载荷和卷吸速度对润滑油膜特性的影响；韩兴等人[12]采用多重网格法对椭圆点接触弹流润滑进行了数值求解；宋大同和刘晓玲[13]采用多重网格法对等温条件下有限长线接触弹流润滑进行了数值分析；欧阳天成等[14]采用多重网格法对有限长线接触的直齿轮弹流动压润滑进行了数值求解。

为了探究冲击载荷对滚滑轴承润滑性能的影响，本文作者设计一种轮子扁疤系统来模拟轴承工作中受到的循环冲击载荷，利用多重网格数值分析法对比研究冲击载荷作用下滚滑轴承和滚动轴承的润滑特性，以了解滚滑轴承润滑油膜抗冲击性能的优劣，观察分析冲击载荷作用下的不同工况对滚滑轴承滚子润滑的影响。

1 循环冲击载荷的数学模型

轴承是装在旋转系统中进行承载运动的，如车辆的轮轨系统，由于受载塑性变形或磨损等造成的扁疤缺陷，具有该缺陷的轮子在运行过程中产生的冲击载荷会周期性地作用在轴承上，其产生的循环冲击载荷模型如图1所示。

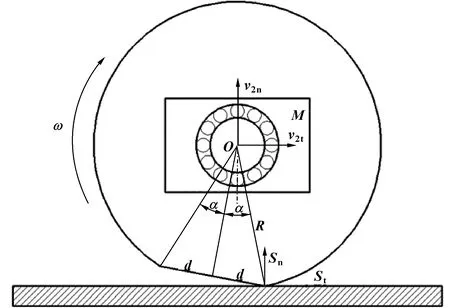
图1 循环冲击载荷模型Fig 1 Cyclic impact load model

以轴承内圈中心点O为坐标原点，且与轴固定连接，外圈与质量为M的轮子固定连接。假设轮子半径为R，轮子扁疤长度为2d，以角速度ω转动。碰撞前车轮O点速度为v1，角速度为ω1，车轮转动惯量为Jc。当轮子扁疤接触轨道，扁疤右侧边界产生碰撞，冲撞过后，O点切向速度为v2t、法向速度v2n，角速度为ω2。

碰撞冲量方程：

M(v2t-v1cosα)=St

(1)

M(v2n+v1sinα)=Sn

(2)

扭矩冲量方程：

-J(ω2-ω1)=R(Stcosα+Snsinα)

(3)

式中:St代表车轮扁疤边界冲撞点切向冲量;Sn代表车轮扁疤边界冲撞点法向冲量。

假定e为碰撞恢复系数，有碰撞前后速度等式：

v2n-Rω2sinα=e(v1sinα+Rω1sinα)

(4)

v2t-Rω2cosα=0

(5)

由关系式(1)—(5)知，轴承内圈受到法向方向的冲击速度v2n为

(6)

扁疤处法向冲量Sn为

(7)

由于碰撞冲击的特点是碰撞时间τ极短，假设碰撞时轮轨接触处不发生滑动，则法向方向的平均碰撞力Fn为

(8)

2 滚子弹流润滑模型构建及数值计算

2.1 滚子弹流润滑的数学模型

由于冲击载荷的作用，在滚子与滚道接触处会产生弹性变形，根据Hertz接触理论，可将之转换为具有当量曲率半径R和当量弹性模量E的弹性圆柱与刚性平面的接触问题。如图2所示，h(x)是x处的膜厚，h0是未变形前滚子与轨道的间距，v(x)是x处的弹性变形，x2/(2R)是由滚子母线产生的原始几何间隙。

图2 滚子的弹流润滑模型Fig 2 EHL model for rollers

为简化计算，文中不考虑挤压油膜温度对润滑油特性的影响，也不考虑滚子歪斜偏移导致接触线偏移或失效，只考虑润滑性质为线接触等温弹流润滑。由一般Reynolds方程可得滚子线接触等温弹流润滑方程：

(9)

式中：p为润滑油膜压力(Pa);h为接触处油膜厚度(m);ρ为润滑油密度(kg/m3);η为润滑油黏度;U为卷吸速度(m/s)。

任意点x处的油膜厚度方程：

(10)

弹流润滑变形方程：

(11)

式中:c为待定常数;s为载荷到坐标原点的距离。

等温条件下的黏压方程:

(12)

润滑油的密压方程：

(13)

式中:ρ0为大气压力下的润滑油密度;常数A一般取值0.6，常数B一般取值1.7。

设定承载体(滚子、滑块)与轴承套圈为线接触，滚子与滑块均匀布置且对应的圆心角相等，则最大负载的承载体受力Qmax=4.6Fn/Z,式中Z为承载体个数。最大承载滚子的油膜压力与其受载平衡方程：

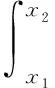
(14)

通过方程(9)—(14)得出冲击载荷作用时滚子弹流润滑油膜的膜厚及压力。

2.2 滚子弹流润滑特性的数值计算

将方程(8)—(14)量纲一化和离散化处理后按多重网格法进行数值计算。由于黏压方程中的黏度和膜厚方程中的弹性变形均随压力变化而变化，因此先给定一个大于h0的初始油膜厚度值和常压下的润滑油黏度值η0，通过式(9)计算油膜压力;将计算得到的油膜压力代入式(11)、(12)计算弹性变形和黏度;将计算得到的弹性变形代入式(10)计算新的油膜厚度值，再将计算得到的油膜厚度值和黏度代入式(9)，进行新一轮的油膜压力、弹性变形、黏度和油膜厚度的计算。重复计算直至两次迭代计算得到的压力差Δ符合精度要求，迭代计算结束，输出得到最终的压力和油膜膜厚。计算流程如图3所示。

图3 计算流程Fig 3 Calculation flow

2.3 模型验证

由上述数学模型计算各节点的压力P、原有厚度H1、原有厚度H2、变形值V，可得纵坐标为厚度、压力及变形的滚子接触变形前后量纲一化值，如图4所示。可知，滚子变形前圆弧表面在接触变形后呈水平一字形，在无润滑油时一字接触表面之间间隙为0，接触面压力呈圆弧状对称分布，中间点压力最高，接触区外滚子表面变形量为负值，表面曲率略有增大。计算结果与线接触弹性变形的理论结果相吻合，表明所建计算模型基本正确。

图4 滚子弹性接触变形前后对比Fig 4 Comparison before and after elastic contact deformation of rollers

3 滚滑轴承滚子的润滑特性及其比较

3.1 滚滑轴承的结构与工况

滚滑轴承及轮子的零件材料为GCr15，参照NU2214圆柱滚子轴承尺寸[15]，设定滚滑轴承及轮子模型的结构参数如表1所示，润滑工况参数如表2所示。

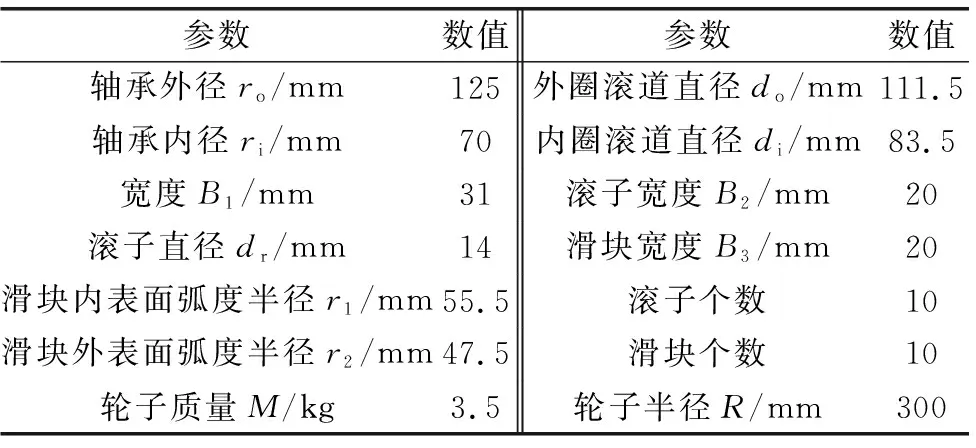
表1 几何结构参数Table 1 Geometrical structure parameters

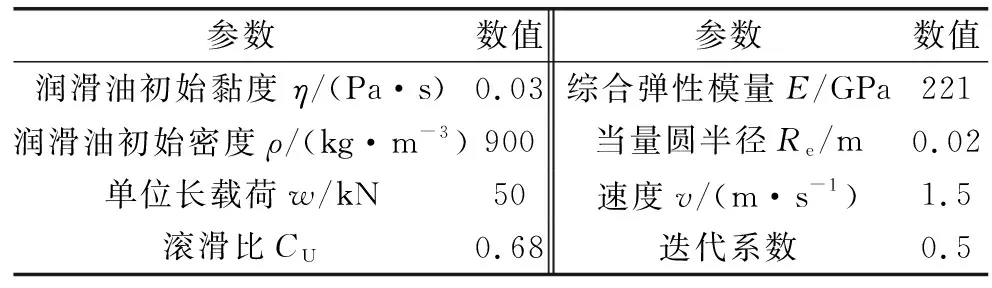
表2 润滑工况参数Table 2 Parameters of lubrication condition

3.2 滚滑轴承滚子的油膜厚度和压力

恒温循环冲击载荷作用下的数值计算时，赋予总节点数N为101，选取接触面润滑油入口量纲一参数X0=-2，出口量纲一参数XE=1.5，设定载荷冲击时长为tΔ，0.5tΔ为载荷冲击最大值发生时，按图3中的计算步骤进行计算，得出各位置节点X的量纲一油膜压力值P和量纲一油膜厚度值H。冲击载荷作用下滚滑轴承滚子不同时刻下的油膜厚度及压力分布如图5所示。

图5 冲击载荷作用下滚滑轴承滚子不同时刻的油膜厚度及压力分布Fig 5 Oil film thickness and pressure distribution of the roller of rolling-sliding bearing under impact load at different times (a)t=0;(b)t=0.16tΔ; (c)t=0.33tΔ;(d)t=0.5tΔ

由图5可知，冲击载荷发生前(t=0时刻)，滚子量纲一中心油膜厚度值为0.7，油膜第二峰值压力高于中心压力，油膜出口区有明显缩颈现象，滚子处于稳定润滑状态。冲击载荷最大时的0.5tΔ时刻，滚滑轴承滚子的最小油膜厚度为0.1，油膜第二峰值压力明显小于中心压力。这是因为出口处油膜压力陡然减小，小于滚子接触处的弹性变形力，材料产生局部回弹，从而出现油膜的厚度缩颈和第二压力峰值。

3.3 滚动轴承滚子的油膜厚度和压力

为便于了解冲击载荷作用下滚滑轴承润滑性能的优劣，将滚滑轴承的滑块换成滚子并附加保持架，滚滑轴承即变成滚动轴承，在相同条件下得到滚子各时刻的油膜厚度及压力分布如图6所示。

由图6可知，冲击载荷发生前(t=0时刻)，滚子量纲一中心油膜厚度值为0.6，油膜第二峰值压力高于油膜中心压力，油膜出口区有明显缩颈现象，滚子处于稳定润滑状态。冲击载荷处于0～0.16tΔ时刻，滚子油膜厚度从0.6迅速降到0.25；冲击载荷处于0.16tΔ～0.33tΔ时刻，滚子油膜厚度从0.25下降到0.1，膜厚下降速率逐渐减慢；冲击载荷最大时的0.5tΔ时刻，油膜压力第二峰值完全消失，最小油膜厚度为0.09。原因与滚滑轴承的相似，只是滚子承受冲击载荷更大、更迅速。

对比分析滚滑轴承和滚动轴承的滚子润滑特性可知，冲击载荷发生前(t=0时刻)，2种轴承的滚子油膜第二峰值压力均高于油膜中心压力，油膜出口区有明显缩颈现象，滚滑轴承的滚子中心油膜厚度略大于滚动轴承；冲击载荷达到最大值的过程中(0～0.5tΔ)，2种轴承的滚子中心油膜厚度迅速下降，其变化规律相同，油膜压力第二峰值减小并向接触出口区移动，膜厚缩颈现象逐渐消失；冲击载荷最大时的0.5tΔ时刻，滚滑轴承的滚子油膜厚度略大于滚动轴承，且油膜压力曲线第二峰值并未完全消失，而滚动轴承滚子的油膜压力曲线第二峰值完全消失，滚滑轴承的滚子润滑性能受冲击载荷的影响要小于滚动轴承。

4 不同工况对滚滑轴承滚子润滑的影响

4.1 润滑油初始黏度的影响

以冲击载荷作用最大时刻0.5tΔ、初始速度为1.5 m/s，润滑油初始黏度η0分别为0.02、0.05、0.10 Pa·s为条件，分析润滑油黏度对滚子弹流润滑状态的影响。以输出接触面节点为横坐标，量纲一油膜厚度值为纵坐标，结果如图7所示。

由图7可知，初始黏度为0.02、0.05、0.1 Pa·s时，接触中心量纲一膜厚分别为0.073、0.141、0.235，油膜厚度随初始黏度的增加而增加，尽管润滑油黏度发生改变，但油膜缩颈现象并未消失，油膜厚度分布依旧接近滚子纯弹性变形的分布，适当提高润滑油黏度有助于保持冲击载荷下滚子的油膜厚度。

图7 润滑油初始黏度对油膜厚度分布的影响Fig 7 Effect of initial viscosity of lubricating oil on oil film thickness distribution

4.2 轴承初始速度的影响

以冲击载荷作用最大时刻0.5tΔ，润滑油黏度为0.02 Pa·s，初始速度U0分别为1.5、2.2、3.0 m/s为条件，分析轴承速度对滚子弹流润滑油膜状态的影响。以输出接触面节点为横坐标，量纲一油膜厚度值为纵坐标，结果如图8所示。

由图8可知，初始速度为1.5、2.2、3 m/s时，中心量纲一油膜厚度分别为0.073、0.098、0.122，滚子弹流润滑中心膜厚随初始速度的增大而增加，但增加的幅度不大。随速度的增加，油膜出口处缩颈现象越加明显，中心膜厚和缩颈膜厚的差值从0.003增长到0.01，增大了3倍。油膜出口缩颈现象对速度比较敏感，增大轴承转速有利于润滑油膜的形成，也有利于增大膜厚缩颈变形程度，可见适当提高轴承速度有助于冲击载荷下滚子的润滑。

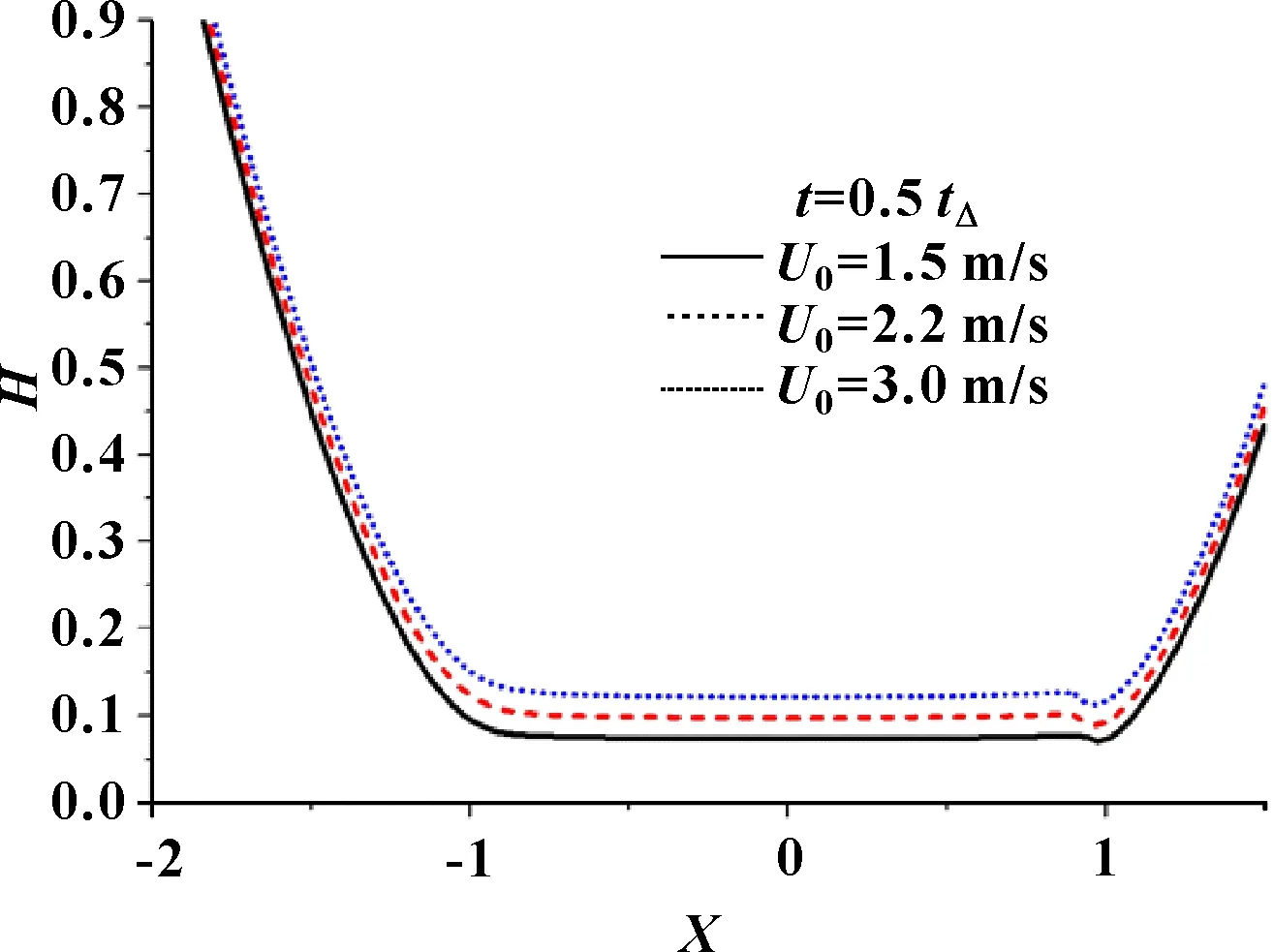
图8 轴承初始速度对油膜厚度分布的影响Fig 8 Effect of bearing initial velocity on oil film thickness distribution

4.3 冲击载荷频率的影响

设定初始量纲一油膜厚度值为0.05，量纲一冲击载荷为1 000，油膜厚度值随冲击载荷作用周期的变化如图9所示。

图9 不同冲击载荷频率对膜厚的影响Fig 9 Effect of impact load frequency on film thickness (a)the frequency is 0.08 s;(b)the frequency is 0.05 s;(c)the frequency is 0.036 s;(d)the frequency is 0.025 s

由图9可知，周期分别为0.08、0.05、0.36和0.25 s的冲击载荷W作用于轴承滚子时，油膜厚度H也发生周期性变化，变化周期和载荷变化周期一致。冲击载荷作用周期为0.08 s时，最低量纲一油膜厚度为1.58，冲击载荷作用周期为0.025 s时，最低量纲一油膜厚度为2.23，这是由于冲击载荷周期越短，越多的润滑油来不及被挤出，停留在接触区域形成挤压效应油膜，说明冲击载荷变化速率越快，挤压油膜效应越强，最小油膜厚度越大。

4.4 冲击载荷幅值的影响

设定初始量纲一油膜厚度值为0.05，冲击载荷变化周期为0.05 s，冲击载荷的不同幅值对油膜厚度值的影响如图10所示。

由图10可知，随着冲击载荷幅值的增加，最小油膜厚度值降低且油膜回升值也降低，如1倍冲击载荷幅值作用时，量纲一最小膜厚值为1.93，油膜回升量纲一膜厚值为3.9；在4倍冲击载荷幅值作用时，量纲一最小膜厚为1.0、油膜回升量纲一膜厚值为2.36。冲击载荷幅值对油膜厚度影响很大，幅值越大的冲击载荷作用到滚子上，接触区的润滑油被挤出越多，形成挤压效应的油膜越少，形成的油膜厚度越薄。由此可知，冲击载荷的幅值对滚子弹流润滑影响显著，大幅值的冲击载荷会迅速降低油膜厚度，影响润滑油的稳定性。

图10 冲击载荷幅值对油膜厚度的影响Fig 10 Effect of impact load amplitude on oil film thickness (a)one time amplitude; (b)2 times amplitude;(c)3 times amplitude;(d)4 times amplitude

5 结论

(1)冲击载荷发生前，滚滑轴承与滚动轴承的滚子油膜均有高于油膜中心压力的第二峰值压力，油膜出口区有明显的缩颈现象，滚滑轴承的滚子油膜厚度略大于滚动轴承；冲击载荷增至最大时，滚滑轴承的油膜第二峰值压力虽会逐渐减小，但不会消失。

(2)冲击载荷作用下滚子油膜厚度随润滑油黏度的增加而增加，适当提高润滑油黏度有助于保持润滑油膜厚度。

(3)滚子油膜厚度随转速增大而增加，油膜出口处缩颈现象表现更明显，提高轴承转速有助于冲击载荷作用下滚子油膜厚度的保持。

(4)冲击载荷作用频率越大，油膜耐挤压能力越强，油膜厚度越大。

(5)冲击载荷的幅值越大，滚子油膜厚度越薄，幅值过大的冲击载荷会迅速降低油膜厚度，严重影响润滑油膜的稳定性。