双S型辐板车轮对钢轨波磨的影响*

张银仙 陈光雄 杨普淼 康 熙

(西南交通大学摩擦学研究所 四川成都 610031)

钢轨波浪形磨耗，简称钢轨波磨，是指在钢轨上与车轮接触的表面产生的波浪形不均匀磨耗。GRASSIE等[1]结合历年学者的研究，提出波磨的2种形成机制，即固定波长机制和损伤机制，并据其将波磨分类，总结了所有波磨类型的特征、形成原因以及缓减措施，为后续研究提供了重要参考。SATO等[2]鉴于波磨在日本盛行的现象以及波磨发生机制和对应措施的不完善，详尽地回顾和分析了国内外学者对于钢轨波磨的研究。金学松等[3]通过大量的文献研究，将波磨成因理论归纳为自激振动理论、反馈振动理论和其他理论。基于自激振动理论，陈光雄等[4-5]提出的蠕滑力饱和导致系统发生摩擦自激振动从而引发钢轨波磨的机制，可以较为完善地解释小半径曲线上低轨普遍发生波磨而高轨鲜有波磨的现象。文献[6-9]对该理论模型的应用，进一步验证了轮轨摩擦自激振动导致波磨理论的正确性。

目前，钢轨打磨是最有效的消除波磨的措施[10]。但是，打磨这项维修工程耗时耗力，是一种非常被动的解决措施，科研人员们更倾向于从波磨形成机制出发去研究抑制或消除波磨的措施。刘学毅和印洪[11]基于轮对黏滑振动形成波磨的理论，提出将曲线段发生波磨的钢轨置换到直线段上、增加轨道弹性和阻尼等措施来减缓波磨。张胜等人[12]、张喻涵等[13]基于摩擦自激振动理论，分别研究了轮对结构优化和直辐板车轮对波磨抑制的积极作用。然而，目前对波磨的研究仅局限于单S型辐板和直辐板车轮，针对双S型辐板车轮却鲜有研究。因此本文作者就双S型辐板车轮的钢轨波磨性能展开了讨论，首先基于轮轨摩擦自激振动导致钢轨波磨的理论，分别建立了正反双S型辐板轮对[14-15]有限元模型;然后采用复特征值分析方法，研究当地铁通过小半径曲线时，双S型辐板车轮对钢轨波磨的影响；同时，与单S型辐板车轮进行对比分析。

1 理论和模型

1.1 复特征值分析方法

复特征值分析法被广泛应用于制动噪声的研究，是一种通过模态分析预测系统稳定性的方法。而CHEN等[5]在使用复特征值法研究钢轨波磨问题时，发现YUAN[16]提出的方法可以有效地模拟轮轨之间的摩擦耦合，轮轨系统的动力学方程如下：

(1)

式中：M、C、K分别表示系统的质量矩阵、阻尼矩阵、刚度矩阵，为非对称矩阵。

方程(1)的特征方程为

(Mλ2+Cλ+K)φ=0

(2)

式中：λ表示方程的特征值；φ表示特征向量。

求解得方程(2)的通解为

x(t)=∑φiexp[(αi+jβi)t]

(3)

式中:φi是第i阶特征向量;αi+ jβi是其对应的第i阶复数特征值。显而易见，当特征值的实部αi>0时，位移将会随着时间的增加而增加，即，系统的振动将会趋于不稳定。相应地，定义等效阻尼比ξ作为评判系统稳定性的参数，如下所示：

ξ=-2Re(λ)/|Im(λ)|

(4)

因此，当系统的等效阻尼比为负数时，系统可能发生不稳定振动，并且，等效阻尼比的绝对值越大，越容易发生不稳定振动。较为详细的摩擦自激振动复特征值理论请参见文献[5,17]。

1.2 双S辐板车轮有限元模型

据王庆峰[18]统计，上海4号线使用的ZD840型车轮为双S辐板车轮，这种类型的车轮辐板有较好的变形能力。文中针对双S型辐板车轮，研究其对钢轨波磨的影响。如图1所示为3种不同辐板车轮的二维截面图。其中，图1(a)为传统的双S型辐板车轮，规定其S弯方向为正方向，由此可建立反双S辐板车轮如图1(b)所示。为验证模型的正确性，以图1(c)所示的传统单S型辐板车轮进行对比分析。

图1 3种不同辐板车轮截面Fig 1 Section for three wheels with different web plates (a)positive double S plate wheel;(b)negative double S plate wheel;(c) single S plate wheel

根据图1分别建立了正双S型辐板车轮、反双S车轮和单S型车轮的有限元模型，如图2所示。单元类型均采用非协调单元C3D8I。

图2 3种不同辐板车轮有限元模型Fig 2 FEM model for three wheels with different web plates (a)positive double S plate wheel;(b)negative double S plate wheel;(c) single S plate wheel

针对3种辐板车轮分别建立地铁小半径曲线轮轨系统有限元模型，包括一个轮对、两条36 m长的钢轨和系列短轨枕，如图3所示。轮对和钢轨的弹性模量为210 GPa，泊松比为0.3，密度为7 800 kg/m3。轨枕的弹性模量为190 GPa，泊松比为0.3，密度为2 800 kg/m3。

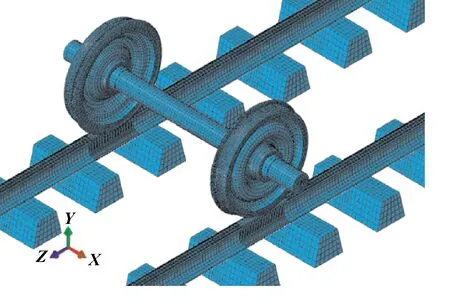
图3 轮轨系统有限元模型Fig 3 FEM model of wheelset-track system

轮对和钢轨之间采用面面接触，钢轨和轨枕之间、轨枕和地基之间均通过阻尼弹簧对连接，轮轨接触模型如图4所示[5]。文中研究工况是半径R≤350 m的地铁线路，通过在轮对两端施加悬挂力(FSVL，FSLL，FSVR，FSLR)来实现，NL和NR，FL和FR分别是轮轨接触点的法向力和蠕滑力。关于图4中各参数介绍如表1所示。

图4 轮轨系统接触模型Fig 4 Contact model of the wheelset-track system

表1 模型参数介绍Table 1 The introduction of model parameters

2 计算结果及分析

2.1 3种辐板车轮对比分析

针对图1所示3种辐板车轮，分别建立了轮轨系统有限元模型并进行计算，得到负等效阻尼比分布情况如图5所示。

图5(a)所示为正双S辐板车轮模型的计算结果，发现没有负等效阻尼比，即无波磨产生。为了校验模型，对传统的单S辐板车轮模型进行了计算，如图5(c)所示，计算得到2个负等效阻尼比，主频率为501.26 Hz，对应的等效阻尼比为-0.023 81，与文献[5]中的结果一致，从而证实了无波磨模型的正确性。

反双S辐板模型的计算结果如图5(b)所示。可见有4个不稳定频率产生，主频率为431.4 Hz，对应的等效阻尼比为-0.028 3。所以相较于单S车轮和反双S车轮，正双S辐板车轮显然消除了波磨。这可能是因为正双S辐板比单S辐板弯曲较大，变形能力相对较好[18]；而比反双S辐板结构较优，对车轮的强度和刚度有积极的影响。

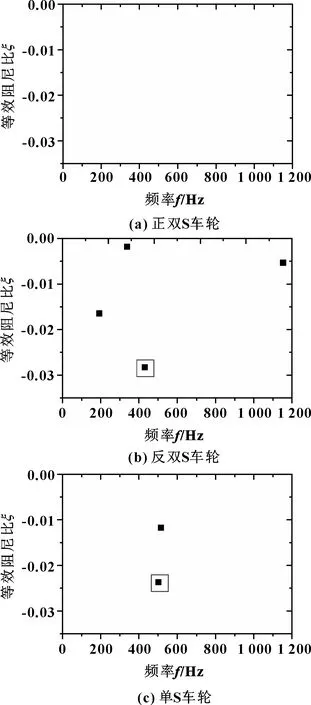
图5 3种辐板车轮等效阻尼比分布Fig 5 Distribution of effective damping ratio for three wheels with different web plates (a)positive double S plate wheel;(b)negative double S plate wheel; (c) single S plate wheel

2.2 双S辐板弯曲程度对钢轨波磨的影响

如图6所示为不同弯曲程度的正双S辐板车轮截面图，弯曲程度由大到小分别规定为大弯、中弯和小弯。建立相对应的三维有限元模型进行计算，结果显示均无负等效阻尼比产生，说明正双S辐板弯曲程度对钢轨波磨没有影响。

图6 正双S辐板不同弯曲程度截面Fig 6 Section of wheels with different double S-type web sizes (a)big bend;(b)middle bend;(c)small bend

同样，根据图7所示的反双S不同弯曲程度分别建立轮轨系统模型，计算了等效阻尼比分布，结果如图8所示。

图7 反双S辐板不同弯曲程度截面Fig 7 Section of wheels with different negative double S-type web sizes (a)big bend;(b)middle bend;(c)small bend

图8 不同弯曲程度的反双S辐板车轮等效阻尼比分布Fig 8 Distribution of effective damping ratio for the wheels with different negative double S-type web sizes

根据图8，反双S大弯模型产生4个不稳定振动频率，其中主频率为f=431.40 Hz，对应的等效阻尼比为ξ=-0.028 30。中弯模型也产生4个不稳定振动频率，但是完全抑制了大弯模型产生的二阶频率339.73 Hz；主频率为f=424.03 Hz，等效阻尼比为ξ=-0.021 71，相较于大弯模型均有所降低。小弯模型产生3个不稳定振动频率，主频率为f=420.21 Hz，等效阻尼比为ξ=-0.008 55，相较于中弯模型均有所降低，并且抑制了中弯模型产生的一阶频率162.85 Hz。总体来看，对于反双S辐板模型，弯曲程度越大，轮轨系统越容易产生不稳定振动。这一结果与张喻涵等[13]的研究结果一致：直辐板有抑制波磨的能力，而小弯辐板趋近于直辐板，因此小弯模型更加稳定，大弯辐板车轮则可能是由于结构强度不够导致了轮轨系统的不稳定。

不同弯曲程度反双S辐板车轮对应的3个轮轨系统对应的主要振型如图9所示。可见不稳定振动主要发生在低轨内轮，与实际相符。

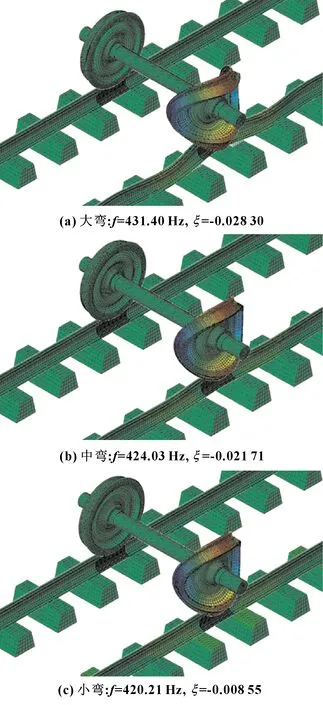
图9 轮轨系统不稳定振动模态Fig 9 Mode shapes of unstable vibration for the wheelset-track system (a)big bend(f=431.40 Hz,ξ =-0.028 30); (b)middle bend(f=424.03 Hz,ξ =-0.021 71); (c)small bend(f=420.21 Hz,ξ =-0.008 55)

2.3 双S辐板厚度对钢轨波磨的影响

由以上两小节分析讨论可知，正双S型辐板车轮是一种无波磨车轮，且辐板弯曲程度对结果无影响，而反双S辐板车轮易产生波磨。所以，本节讨论辐板厚度对波磨的影响，选取中等弯曲程度的正双S型辐板车轮，辐板厚度t分别为33、23、13 mm，截面示意图如图10所示。

建立与图10相对应的车轮的有限元模型，计算结果显示33和23 mm厚度的辐板车轮均不发生不稳定振动，而13 mm厚度的车轮产生一个1 125.5 Hz的不稳定振动频率，对应等效阻尼比为-0.000 10。说明正双S辐板厚度对波磨影响不大，这可能是因为正双S辐板结构本身的稳定性是由其正双S弯决定的，与其辐板厚度关系较少，但也应综合性能、强度、经济等原则选取适当的辐板厚度。

图10 正双S辐板不同厚度截面Fig 10 Section of the wheels with different thickness of the positive double S-type web (a)t=33 mm; (b)t=23 mm;(c)t=13 mm

3 结论

(1)正双S型辐板车轮是一种无波磨车轮，其弯曲程度对结果无明显影响，辐板厚度对波磨影响不大，但也应综合考虑选取适当厚度的辐板车轮。

(2)反双S型辐板容易引起钢轨波磨，且辐板弯曲程度越大，越容易引起轮轨系统不稳定振动。

(3)反双S型辐板模型预测的不稳定振动主要发生在低轨内轮，与实际相符，说明了摩擦自激振动理论的正确性。