采用N-list结构的混合并行频繁项集挖掘算法

刘卫明，张 弛，毛伊敏

江西理工大学 信息工程学院，江西 赣州341000

随着信息技术的快速发展，大数据在互联网、社交网络以及物联网等领域得到了广泛的应用。大数据的出现对工业、医疗以及政府机构在内的许多社会主体具有重要意义。如何快速并准确地从这些海量数据中挖掘出有价值的信息和知识已经成为当今社会迫切需要解决的问题之一。

数据挖掘又称为知识发现（knowledge discover in database，KDD)，其目的在于发现大量数据中有价值的信息。常见的数据挖掘任务有分类、聚类、关联规则等。其中关联规则分析是其重要的研究方向之一。通过对关联规则挖掘算法的研究能够在海量数据中找出有价值的规则，这些规则对企业管理上的决策具有巨大帮助。传统的关联规则挖掘算法主要分为三类：（1）产生-测试方法，此类算法先通过迭代产生候选项集并分别计数，然后根据最小支持度阈值统计得到频繁项集，典型算法是Agrawal 等人提出的Apriori 算法；（2）模式增长方法，此类算法在挖掘过程中不会产生候选项集，而是将所有的频繁项压缩成一种树结构，通过对树的直接遍历挖掘频繁项集，典型算法有FP-Growth、LP-tree等算法；（3）垂直格式方法，此类算法主要是将水平数据集转换成垂直格式，通过交运算来得到频繁项集，典型算法为Eclat 算法。大数据环境下，随着数据量的不断增加，运行时间和内存使用量成为传统关联规则挖掘算法的重要瓶颈，单纯通过提升计算机硬件水平已经不能满足人们对大数据分析与处理的需求。此时并行化的计算思想变得尤为重要，通过改进传统的关联规则挖掘算法，并与分布式计算模型相结合成为当前研究的主要方向。

近年来，Google 开发的MapReduce 并行编程模型由于其操作简单、自动容错、负载均衡、扩展性强等优点深受广大学者和企业的青睐。同时Hadoop作为一种广泛使用的MapReduce 开源框架，不仅实现了对MapReduce 的动态调用，而且在很大程度上促进了MapReduce的应用开发。目前许多基于Map-Reduce 计算模型的关联规则挖掘算法已成功应用到大数据的分析与处理领域中。文献[9-11]采用Apriori 算法多次迭代的思想，在每次迭代过程中启用一个MapReduce 任务，实现了Apriori 算法在大数据领域的应用。然而此类算法在挖掘频繁项集时不仅需要多次扫描事务数据集而且会生成大量候选项集，极大降低了并行算法的挖掘效率。鉴于并行Apriori算法的固有缺陷，文献[12-16]通过将MapReduce 计算模型与FP-Growth 算法相结合提出了并行的FPGrowth 算法。与并行Apriori 算法不同，此类算法在挖掘过程中不产生大量的候选项集，并且只需要扫描两次事务数据集，在每个计算节点上构建局部FPTree 树，通过对局部FP-Tree 树的遍历得到局部频繁项集，然后将其合并得到全局频繁项集。在挖掘频繁项集的过程中，各节点之间计算独立，既不需要相互等待也不需要交换数据，极大提高了并行频繁项集挖掘算法的效率。然而并行FP-Growth 算法在挖掘过程中需要消耗大量的计算资源来递归构建频繁项的FP-Tree 树，且大数据环境下各节点所构造的局部FP-Tree 树的规模十分巨大，对于这些FP-Tree 树的存储需要消耗大量的内存。考虑到并行Apriori 算法与并行FP-Growth 算法的不足，文献[17-19]提出了并行Eclat 算法，此类算法虽然计算简单，在一定程度上克服了从海量事务数据集中挖掘频繁项集时存在计算能力不足的问题，但并行的Eclat 算法需要将水平数据集转化为垂直数据集作为输入数据，然后采用类Apriori 方法迭代挖掘频繁项集，这在大数据环境下是无法实现的。

为了充分利用不同算法各自的优点，减少并行计算中单个节点的内存需求量与节点之间的通信量，Liao 等人提出了一种将dist-Eclat与传统FPGrowth算法相结合的混合算法——MRPrePost 算法。该算法主要分为三个阶段：首先通过调用一次MapReduce 任务得到频繁1 项集F-list；然后构造Flist 所对应的PPC-Tree 树，并对PPC-Tree 树进行先序和后序遍历产生频繁项的N-list；最后对F-list 进行分组，并分布在多个计算节点上进行频繁项集的挖掘。相较于其他单一的并行频繁项集挖掘算法，该算法既能对原始数据集进行无损压缩，又可以快速计算项集的支持度。此外，该算法将对树的挖掘过程转化成与垂直格式交运算类似的N-list 合并过程，并且该过程不需要将PPC-Tree 树保存在内存中，极大减少了算法的计算时间和内存使用量。然而该算法仍存在几个明显不足：（1）在F-list 分组阶段，该算法未能充分考虑到集群负载均衡对算法性能的影响，容易造成数据划分中计算节点负载不均衡的问题；（2）在合并两个频繁项集的N-list 结构时不仅要逐一比较两者中的每一项，而且需要将初步获得的N-list 结构中(先序，后序)序列相同的PP-code 合并，极大地降低了N-list 的合并效率；（3）在并行挖掘频繁项集阶段，该算法是通过合并任意两个-项集的N-list 结构来生成（+1）-项集，会产生大量的冗余搜索。针对上述问题，本文提出了一种基于N-list 结构的混合并行频繁项集挖掘算法（hybrid parallel frequent itemset mining algorithm based on N-list，HPFIMBN）。首先，该算法充分考虑到集群负载对并行算法挖掘效率的影响，设计负载估计函数（load estimation function，LE）用于计算出频繁1 项集中每项的负载量，并提出基于贪心策略的分组方法（grouping method based on greedy strategy，GM-GS），将F-list 中的每一项根据其负载量进行均匀分组，既解决了数据划分中计算节点负载不均衡的问题，又降低了集群中各节点上子PPC-Tree 树的规模。其次，提出预先放弃策略（early abandon strategy，EAS），该策略不仅能避免两个N-list 结构在合并过程中的无效计算，而且不需要遍历初始N-list 结构就能得到最终的Nlist，极大地提高了N-list 结构的合并效率。最后，该算法采用集合枚举树作为搜索空间，并提出超集等价剪枝策略（superset equivalent strategy，SES），来避免挖掘过程中的冗余搜索，生成最终的挖掘结果。实验结果表明，该算法在大数据环境下进行频繁项集挖掘具有较好的效果。

1 相关概念介绍

（PPC-Tree 树）PPC-Tree 树是一种树形数据结构，树中的每个节点均由以下五部分组成：

item-name：节点名称

count：节点计数

pre-order：先序编码

post-order：后序编码

children-list：子节点列表

（PP-code 编码）PP-code 编码又被称为先序后序编码，由pre-order、post-order 和count 三部分组成。对于PPC-Tree 树中的任意节点，称(.-,.-,.)为该节点的PP-code编码。

（祖先孩子关系）给定PPC-Tree 树中任意两节点和(≠)的PP-code，若满足以下关系：

则称节点是节点的祖先节点，为的孩子节点。

（频繁1 项集的N-list）在PPC-Tree 树中，代表相同项的所有PP-code 编码按照先序遍历升序连接生成的序列，被称为频繁1 项集的N-list。

（“ ≺”关系）给定频繁1 项集中的任意两项和，若的支持度大于的支持度，则表示为≺。

（-项集N-list）给定任意两个具有相同前缀的频繁(-1)-项集和，其对应的N-list结构分别表示为：

则-项集的N-list 定义如下：

（1）对于任意(,,)∈-() (1 ≤≤)，(,,)∈-()(1 ≤≤)，若满足条件<，>，则将(,,)加入到的N-list 中，得到初始的N-list。

（2）遍历的N-list，将pre-order 和post-order相同的PP-code 进行合并，得到最终的N-list。

（频繁项集的支持度）给定项集，其N-list 为(,,),(,,),…,(x,y,z)，则项的支持度为++…+z。

2 HP-FIMBN 算法

HP-FIMBN 算法主要包括获取频繁1 项集、频繁1 项集分组和并行挖掘频繁项集3 个阶段。（1）在获取频繁1 项集阶段，启用一次MapReduce 任务，采用类似World Count 方法并行获取频繁1 项集F-list。（2）在频繁1 项集分组阶段，为了避免数据划分中出现计算节点负载不均衡的问题，提出GM-GS 分组方法，该方法先通过负载估计函数LE 计算出频繁1 项集中每一项的负载量，然后根据贪心思想将F-list 进行均匀分组，生成分组列表G-list。（3）在并行挖掘频繁项集阶段，主要包括并行挖掘频繁项集的Map 阶段和Reduce 阶段。在Map 阶段主要是根据前两个阶段生成的F-list 列表和G-list 列表构造出映射路径。在Reduce 阶段首先调用函数在各个计算节点上生成子PPC-Tree 树。然后通过遍历本地PPC-Tree 树，在各个节点上生成局部2-项集的N-list结构。在此过程中为了加快完成N-list 结构的合并任务，提出预先放弃策略EAS，来减少合并过程中的无效计算。最后在挖掘频繁-项集(>2)的过程中采用集合枚举树作为搜索空间，并提出SES 策略，来避免挖掘过程中的重复搜索，生成最终的挖掘结果。

2.1 获取频繁1 项集

对于数据集DB，其频繁1 项集的生成过程主要包括Split、Map、Combine 和Reduce 四个阶段。（1）在Split阶段：使用Hadoop 默认的文件块策略，将原始数据集划分成大小相同的文件块Block，并保存在分布式文件系统（hadoop distributed file system，HDFS）中。（2）在Map 阶段：每个Mapper 节点调用Map()函数对输入文件块Block 进行一次映射，以键值对<=,=1>的形式统计出相应节点中各项出现的次数；同时为了降低集群通信，经过Mapper 节点处理后的数据不会立刻发送给Reduce 节点，而是先进行本地结合。（3）在Combine 阶段：将本地值相同的键值对进行初步合并，然后再以新的键值对作为下一阶段的输入数据传送到Reduce任务中。（4）在Reduce 阶段：需要将输入的键值对进行再次合并，得到每个数据项在整个数据集中的支持度，最后根据最小支持度阈值_筛选出频繁1 项集F-list。

为了更清楚地说明频繁1 项集的获取步骤，本文给出事例，假设事务数据集DB 如表1 所示(_=2)，表2 是针对DB 运行频繁1 项集获取步骤之后得到的F-list。

表1 事务数据集DBTable 1 Transaction database-DB

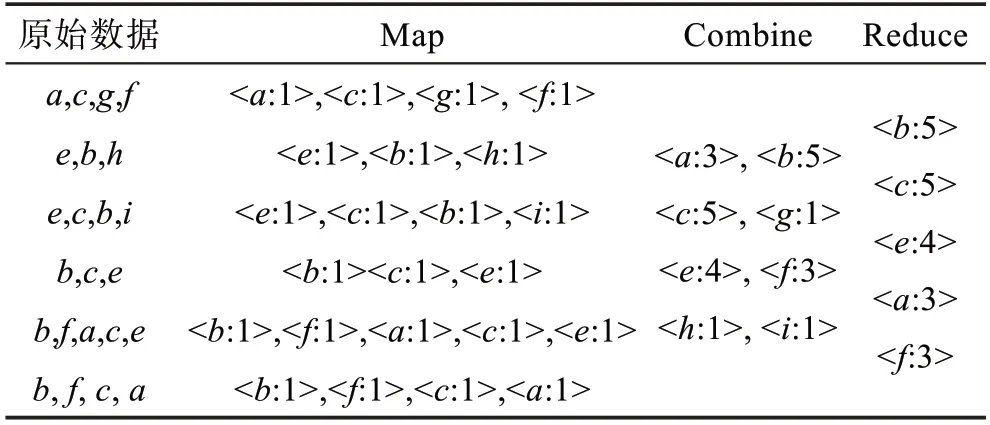
表2 频繁1 项集获取过程Table 2 Process of getting F-list

最终根据支持度降序排序生成的F-list 序列为{:5;:5;:4;:3;:3}。

2.2 频繁1 项集分组

大数据环境下，经过第一阶段获得的频繁1 项集F-list 的规模非常大，导致无法在有限的内存空间中构造PPC-Tree 树。为解决此问题，提出了一种基于贪心策略的分组方法GM-GS。该方法的主要思想是先求取所有频繁1 项集对于分组数量的负载均值，然后为每组分配一个接近负载均值的负载量，从而达到整体的负载均衡。采用GM-GS 分组方法将F-list进行分组时，其关键在于计算频繁1 项集中每一项的负载量，即频繁1 项集中每项所对应的N-list 结构长度。然而N-list 中的元素与PPC-Tree 树中的节点一一对应，在没有构造PPC-Tree 树之前无法准确计算出每一项的负载量。为了解决该问题，在GMGS 方法中通过负载估计函数来预测频繁项的N-list长度。

（负载估计函数LE）若频繁项的支持度是，在F-list 中的位置为，则其负载估计函数如下所示：

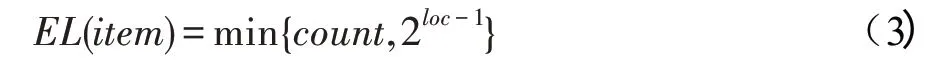
证明 对于频繁项来说，其N-list 的长度表示该项在PPC-Tree 树中的节点个数，显然对于每一项来说，节点数的最大值为该项的支持度。此外在构造PPC-Tree 树时，树中每一项的节点数与其在Flist 中的位置有关。对于频繁项来说，假设其在F-list中的位置为，则最坏情况是排在之前的-1 项中任意项组合在PPC-Tree 中都有对应的路径，且该路径包含项，在此情况下的路径最多有2条。因此频繁1 项集中的每一项的N-list长度不超过该项支持度与2之间的最小值。

采用GM-GS 方法将频繁1 项集F-list 划分为组的分组思想如下：首先根据式（3）计算出频繁1 项集F-list 中每一项的负载量，按照负载量从大到小排序生成L-list；然后计算出所有项对于分组数量的负载均值，将每个负载量大于均值的项分配到负载为0 的组中，并删除该项在L-list 中的信息；最后逆序遍历L-list 剩余的项，若与当前组的负载量_满足式（4），则将项添加到当前组中，更新当前组的负载总量并从L-list 中删除，若不满足式（4），则将项item 添加到下一组，更新分组信息。在分组完毕后，将得到的分组列表G-list 存储到分布式文件系统HDFS 中，使得集群中任意节点都能访问。

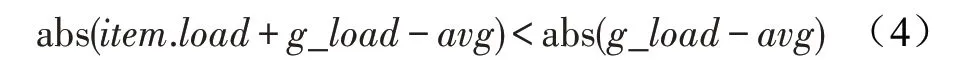
GM-GS 分组方法的形式化如算法1 所示。

GM-GS 分组策略

以表2 中的原始数据为例，若采用GM-GS 分组方法和未采用该方法分别将F-list 分为两组，其结果如表3、表4 所示。

表3 未采用GM-GS 方法对F-list分组Table 3 Without using GM-GS to group F-list

表4 采用GM-GS 方法对F-list分组Table 4 Using GM-GS to group F-list

2.3 并行挖掘频繁项集

采用GM-GS 分组方法对F-list 进行分组是为了将原始数据集中的事务进行重新划分，并把划分后的事务数据集根据分组列表G-list 映射到集群中各个计算节点上，同时在各个节点上构建满足内存要求的子PPC-Tree 树，从而进一步完成频繁项集的挖掘任务。在此过程中主要包括Map 阶段和Reduce 阶段。（1）在Map 阶段：首先根据频繁1 项集F-list 和分组列表G-list 构建哈希表，然后结合哈希表将原始事务集映射到集群中不同的计算节点上，生成映射路径。（2）在Reduce 阶段：集群各节点首先调用_()函数生成子PPC-Tree 树。然后通过对本地PPC-Tree 树的遍历生成局部2-项集的N-list 结构，其中在N-list 合并过程中，为了加快完成N-list 合并任务，避免合并过程中的无效计算，提出一种预先放弃策略EAS。该策略可以通过比较项集支持度与最小支持度阈值的关系来预先判定是否为频繁项集。最后在挖掘频繁-项集(>2)的过程中采用集合枚举树作为搜索空间，并提出SES 策略，来避免挖掘过程中的冗余搜索，生成最终的挖掘结果。

在并行挖掘频繁项集的Map 阶段，其主要任务是将原始事务集根据哈希表映射到集群中不同的计算节点上，具体过程为：首先，从分布式文件系统HDFS 中读取全局频繁1 项集F-list 和分组列表G-list，并将G-list 每组所包含的项作为，组号作为构建HTable。然后，依次读取每一条记录，逆序遍历该记录中的项，根据之前获得的HTable，确定其组号，并以为，排在项之前所有项为组成键值对。与此同时，为了避免同一条记录多次映射到同一节点，删除HTable 中等于的所有键值对。若在映射时找不到对应的组号，则读取前一项执行相同的操作，直到该记录遍历完毕。最后，将所得的结果作为Reduce 阶段的输入传送给Reduce函数。该操作过程伪代码如算法2所示。

并行挖掘频繁项集的Map 阶段

输入：原始数据集data，频繁1项集F-list，分组列表G-list。

输出：映射路径<=,=>。

以表2 中的原始数据为例，若采用GM-GS 方法，经过Map 阶段处理后，分配到Reduce 阶段的各组数据如表5 所示；若未采用GM-GS 方法，分配到Reduce阶段的各组数据如表6 所示。

表5 采用GM-GS 方法后分配到Reduce阶段的各组数据Table 5 Each group data allocated to Reduce stage by using GM-GS method

表6 未采用GM-GS 方法后分配到Reduce阶段的各组数据Table 6 Each group data allocated to Reduce stage without using GM-GS method

在Reduce 阶段，首先调用_()函数在集群各节点生成子PPC-Tree 树，并对PPC-Tree 树进行先序、后序遍历生成2-项集的N-list 结构；然后提出EAS 策略来加快完成两个频繁项集N-list 结构的合并过程，最后采用集合枚举树作为搜索空间，同时提出SES 策略来避免挖掘过程中的冗余搜索，生成最终的挖掘结果。

在并行挖掘频繁项集的过程中最主要的一步是通过合并两个频繁-项集的N-list 结构生成频繁(+1)-项集，如何降低合并过程的运行时间是该算法的关键所在。为此本文提出了一种预先放弃策略EAS，该策略不仅能减少两个频繁项集N-list 结构在合并过程中的无效计算，而且不需要遍历初始N-list结构就能得到最终的N-list，极大提高了N-list结构的合并效率。

给定任意两个频繁-项集，其N-list 分别表示为-和-，长度为和，具体形式如下：

采用EAS 策略合并-和-的具体过程如下：

首先根据性质2 分别计算出-和-的支持度、，并将、求和得到两个N-list结构的总支持度；然后对于任意一个PP-code C，若不满足定义5，则用总支持度减去C.来更新总支持度，其中如果总支持度小于最小支持度阈值则认为当前所比较的项集是非频繁的，提前结束比较过程。EAS 策略伪代码如下：

EAS 策略

输入：-,-，最小支持度_。

输出：合并结果-。

为了说明EAS 策略能够提高N-list 结构的合并效率，以表2 中的原始数据为例构建PPC-Tree 树，如图1 所示，并根据定义3 可知节点与节点的Nlist 结构分别为{(4,10,5)}，{(5,3,1),(7,6,3)}。若采用MRPrePost 算法中的合并策略将频繁项、合并为2 项集需要4 步（表7 第2 列），尤其是在第3 步时需要遍历初始N-list 结构，将PP-code 相同的元素进行合并得到最终的N-list 结构；然而，采用EAS 合并策略只需要3 步，并且不需要遍历初始N-list 结构即可获得最后结果（表7 第3 列）。对于任意的两个频繁(-1)-项集和，其N-list 结构长度分别为和，合并后的初始N-list 长度为，对于MRPrePost 算法来说其时间复杂度为(++)，而采用预先放弃策略其时间复杂度为(+)。

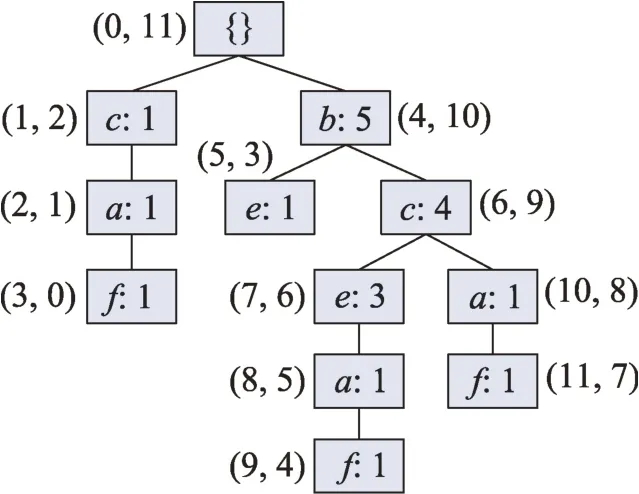
图1 PPC-Tree树Fig.1 PPC-Tree

表7 两种N-list结构合并方法对比Table 7 Comparison of two methods for merging N-list

由于在MRPrePost 算法中主要采用类Apriori 的方法来挖掘频繁项集，这会导致在挖掘过程中出现大量的冗余搜索。为了优化算法的挖掘效率，本文在挖掘频繁项集时采用集合枚举树作为搜索空间，并且提出了一种超集等价策略SES 来避免挖掘过程中的冗余搜索，并生成最终的挖掘结果。

给定一组项集={,,…,i}，其中≺≺…≺i，则集合枚举树的构造过程如下：（1）创建根节点；（2）依次取出项集中的每一项i(1 ≤≤)作为根节点的孩子节点；（3）树中每个节点需要与F-list左侧的每个节点分别做交集，从而生成该节点的孩子节点；（4）重复过程3 直到产生所有的叶子节点。以2.1节得到的F-list为例，构造的集合枚举树如图2 所示。

（超集等价策略）给定项集和项，如果的支持度()等于⋃{}的支持度(⋃{})，那么对于任何项集(⋂=∅∧∉)满足以下关系：

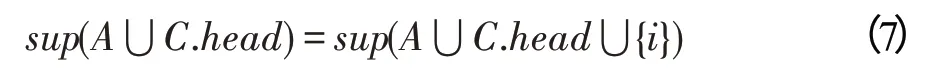
对于项集，其支持度等于⋃{}的支持度，这说明任何包含的事务也包含项，给定一个事务，若中包含项集⋃，则必包含项集和项集，根据前面知识可以推出事务也一定包含项，也就是说⋃的支持度等于⋃⋃{}。

图2 集合枚举树Fig.2 Set-enumeration tree

图3 剪枝后的集合枚举树Fig.3 Set-enumeration tree after pruning

并行挖掘频繁项集的Reduce过程

输入：映射路径，最小支持度_，频繁1 项集。

输出：频繁项集。

以Map 阶段输出的分组数据为例，并行挖掘频繁项集的Reduce阶段主要分为以下几步：

（1）通过调用insert_tree()函数在各计算节点上构建PPC-Tree 子树。在此过程中为了说明GM-GS对降低PPC-Tree子树规模起到的作用，以表5、表6中的两组数据分别构建PPC-Tree 子树，如图4 所示。可以看出采用GM-GS 分组方法后各计算节点上PPCTree子树的规模大致相同，而未采用GM-GS分组方法导致计算节点上PPC-Tree子树的规模相差较大。

图4 PPC-Tree子树对比Fig.4 Comparison of PPC-Tree

（2）各个计算节点对PPC-Tree 子树进行先序后序遍历，生成所有频繁1 项集的N-list，如表8 所示。在此过程中，相较于MRPrePost 算法，本文采用了GM-GS 分组方法使得每个节点上的PPC-Tree 子树规模大致相同，对树遍历所需时间相差不大，不仅有效解决了各计算节点负载不均衡问题，而且也大大提高了算法的挖掘效率。

表8 各组各节点的N-list序列Table 8 N-list sequence of each node in each group

（3）并行化算法只需要找出以每个组中各项为后缀的所有频繁项集，所有组的频繁项集构成整个挖掘过程的最终结果。对于第二组的两个频繁项、，采用EAS 策略分别找出所有以、为后缀的频繁2 项集。对于项需要合并、和、的N-list得到2 项集、，其N-list分别为(3,7,5)和(5,6,3)；同样对于项分别合并、，、和、的N-list得到2 项集、、，其N-list 分别为(3,7,2)、{(1,1,1),(5,6,2)}和(6,4,1)，根据最小支持度min_sup 可知以为后缀的全部频繁2 项集是,，因此第二组输出的频繁2项集有、、和。同样的对第一组采用相同的方法最终得到的频繁2 项集为、、、。

此外在挖掘频繁-项集的过程中为了避免重复搜索，在每个计算节点中构造本地集合枚举树作为搜索空间（如图5 所示），并采用超集等价策略挖掘频繁项集，其结果如表9 所示。

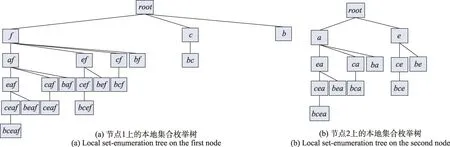
图5 不同节点上的本地集合枚举树Fig.5 Local set-enumeration tree on different nodes

表9 所有频繁项集Table 9 All frequent itemsets

2.4 HP-FIMBN 算法步骤

HP-FIMBN 算法的具体实现步骤如下：

通过Hadoop 默认的文件块策略，将原始数据集划分成大小相同的文件块Block。

对于每一个文件块调用频繁1 项集F-list的生成过程，获得全局频繁1 项集，并将结果存入分布式文件系统HDFS 中。

调用GM-GS 分组方法将F-list 中的每一项进行分组，生成分组列表G-list，并将分组列表存储到HDFS 中。

启动新的MapReduce 任务，在Map 阶段调用算法2 将原始数据集分别映射到各个计算节点上生成映射路径，并在Reduce 阶段调用算法4 来挖掘全局频繁项集。

2.5 算法的复杂度分析

HP-FIMBN 算法主要包括3 个阶段：获取频繁1项集、频繁1 项集分组和并行挖掘频繁项集。因此该算法的时间复杂度主要由三部分组成，分别记为、和。

在获取频繁1 项集的Map 阶段，每个计算节点需要遍历每条记录中的每一项，假设每个节点上的记录数目为，记录的平均长度为，则该阶段的时间复杂度为：

在获取频繁1 项集的Reduce 阶段，需要将Map阶段输出的key 值相同的键值对进行合并，假设每个节点经过Map 阶段输出的键值对个数为N，Mapper节点个数为，则该阶段的时间复杂度为：

因此挖掘频繁1 项集的时间复杂度为：

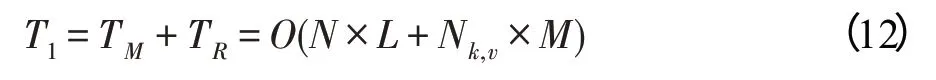
在频繁1 项集分组阶段主要采用GM-GS 策略将F-list 中的每一项进行分组，采用单机即可完成。假设F-list长度为，分组数为，则其时间复杂度为：

在并行挖掘频繁项集过程中，其时间复杂度主要取决于将任意两个具有相同前缀的频繁(-1)-项集和的N-list 结构合并生成-项集的Nlist 结构。假设频繁1 项集-={,,…,I}，以项I结尾的频繁(-1)-项集的N-list 结构长度为L，则采用预先放弃策略的时间复杂度为：

对于HP-FIMBN 算法来说其时间复杂度为：

在MRPrePost 算法中前两个阶段的时间复杂度与HP-FIMBN算法基本相同，而在合并两个频繁(-1)-项集的N-list 结构时，需要遍历初始N-list 结构，将PP-code相同的元素进行合并得到最终的N-list结构，假设-项集的初始N-list 结构平均长度为，其时间复杂度为：

大数据环境下，、相较于的值过小可以忽略不计，而且通常情况下-项集的初始N-list 结构较长，对其遍历以及合并需要消耗较多时间。因此可以得出，HP-FIMBN 算法的时间复杂度远低于MRPrePost算法。

HP-FIMBN 算法的空间复杂度是存储频繁项集及其N-list 结构和集合枚举树所占的内存总和。采用GM-GS 分组方法使得每个计算节点的任务量大致相同，每个子节点的PPC-Tree 规模接近，从而使得频繁项集的N-list 结构规模总体相差不大。假设每个节点平均有g个频繁-项集，每个频繁-项集占（单位为字节：B），频繁-项集的N-list 长度均值为L，频繁-项集的每个N-list 结构占（单位为字节：B）。则存储频繁项集N-list 结构的空间复杂度为(∑g×(+×L))(1 ≤≤)，而集合枚举树的存储只与频繁1 项集的长度有关，其空间复杂度为(×L!)。则HP-FIMBN 算法的空间复杂度为：

MRPrePost 算法的空间复杂度主要是频繁项集及其N-list 结构存储所占的内存。然而该算法采用Hash 映射的分组方法，极易造成计算节点之间负载不均衡的问题。而在算法复杂度分析中采用最差情况，假设集群节点最多有个频繁-项集。则MRPrePost算法的空间复杂度为：

在大数据环境下，频繁项集及其N-list 结构存储所占的内存远远大于集合枚举树存储所需内存，往往可以忽略。因此可知本文算法的空间复杂度小于MRPrePost算法。

3 实验结果及比较

3.1 实验环境

为了验证HP-FIMBN 算法的挖掘性能，本文设计了相关实验。实验环境包括4 个计算节点，其中1个Master 节点，3 个Slaver 节点。所有节点的CPU 均为AMD Ryzen 7，每个CPU 都拥有8 个处理单元，其内存均为16 GB。实验环境中的4 个节点处于同一个局域网中，通过200 Mb/s 以太网相连。软件方面，每个节点安装的Hadoop 版本为2.7.4，JDK 版本为1.8.0，操作系统为Ubuntu 16.04。各个节点的具体配置如表10 所示。

表10 实验环境中各节点的基本配置Table 10 Basic configuration of nodes in experimental environment

3.2 实验数据

HP-FIMBN 算法使用4 个真实数据集，分别为webdocs、kosarak、Susy 和accident。其中webdocs 数据集是由意大利科学家Claudio Lucchese 等人通过网络爬虫抓取的Web 文档数据,该数据集包含1 692 082条数据，共有5 267 656 项，具有数据量多、记录长度长、项数多等特点；kosarak 数据集记录了匈牙利一家大型新闻网站点击流数据，该数据集包括990 002 条数据，共有41 270 项，具有数据量少、项数较多、数据离散等特点；Susy 数据集包含5 000 000 条实例，共有190 项，具有数据量多，记录长度均匀、项数少等特点；accident 数据集是美国近些年发生的交通事故数据，该数据集包含340 183 条数据，共有468 项，具有数据量少、记录长度均匀、项数少等特点。以上数据集均可以在数据挖掘网站下载（http://fimi.ua.ac.be/data/），其具体信息如表11 所示。

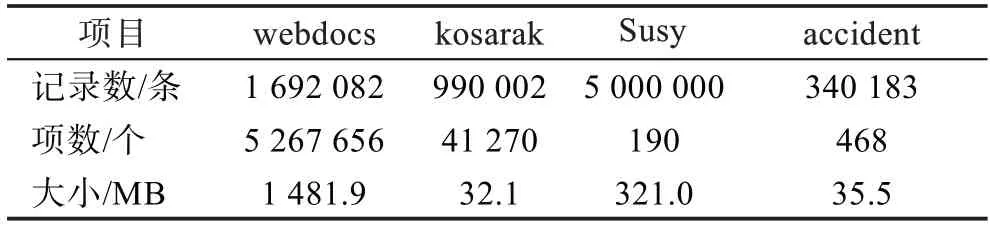
表11 实验数据集Table 11 Experimental data sets

3.3 评价指标

大数据环境下，为验证并行算法的挖掘性能，通常采用加速比作为衡量指标。加速比是指在并行计算下，降低运行时间从而获得的性能提升，其定义为：

其中，表示算法在单个节点上的运行时间，T表示并行计算时的运行时间，S越大，则表示并行计算所耗费的相对时间较少，集群效率得到提升。

3.4 HP-FIMBN 算法可行性分析

为验证HP-FIMBN 算法在大数据集下挖掘频繁项集的可行性，采用算法的加速比来进行衡量。本文选取最小支持度阈值为1 000、5 000、20 000 和100 000，并在每一支持度下分别将HP-FIMBN 算法应用于上述4 个实验数据集上。在每一数据集上独立运行10 次，取10 次结果的均值。通过对算法加速比的比较，实现对HP-FIMBN 算法性能的综合评估。其实验结果如图6 所示。

从图6 中可以看出，随着支持度的不断增加，HPFIMBN 算法在处理webdocs、Susy 两个规模较大的数据集时具有较高的加速比。而在处理kosarak、accident这样小数据集时，随着节点数量增加，加速比的增加趋势并不明显，甚至当支持度为100 000 时，随着节点数量的增加，加速比呈现下降趋势且小于1。这是由于在数据集规模较小时，数据量远小于集群所能处理的数据量，将原始事务集根据分组列表G-list 划分到不同的计算节点中反而增加了各个节点的时间开销，算法性能易陷入瓶颈。而在处理数据规模较大的webdocs 和Susy数据集时，随着节点个数增加，加速比呈线性增长趋势，甚至当支持度为1 000 时，算法在4 个节点下的加速比分别为3.73 和3.16，比在1 个节点下分别提升了2.73 和2.16，这是由于在大规模数据集下，算法能够并行挖掘局部频繁项集和合并频繁项集的优点被逐渐放大，算法的挖掘性能得到极大提高。同时这也表明HP-FIMBN算法适用于大数据集的处理，且具有较强的扩展性。

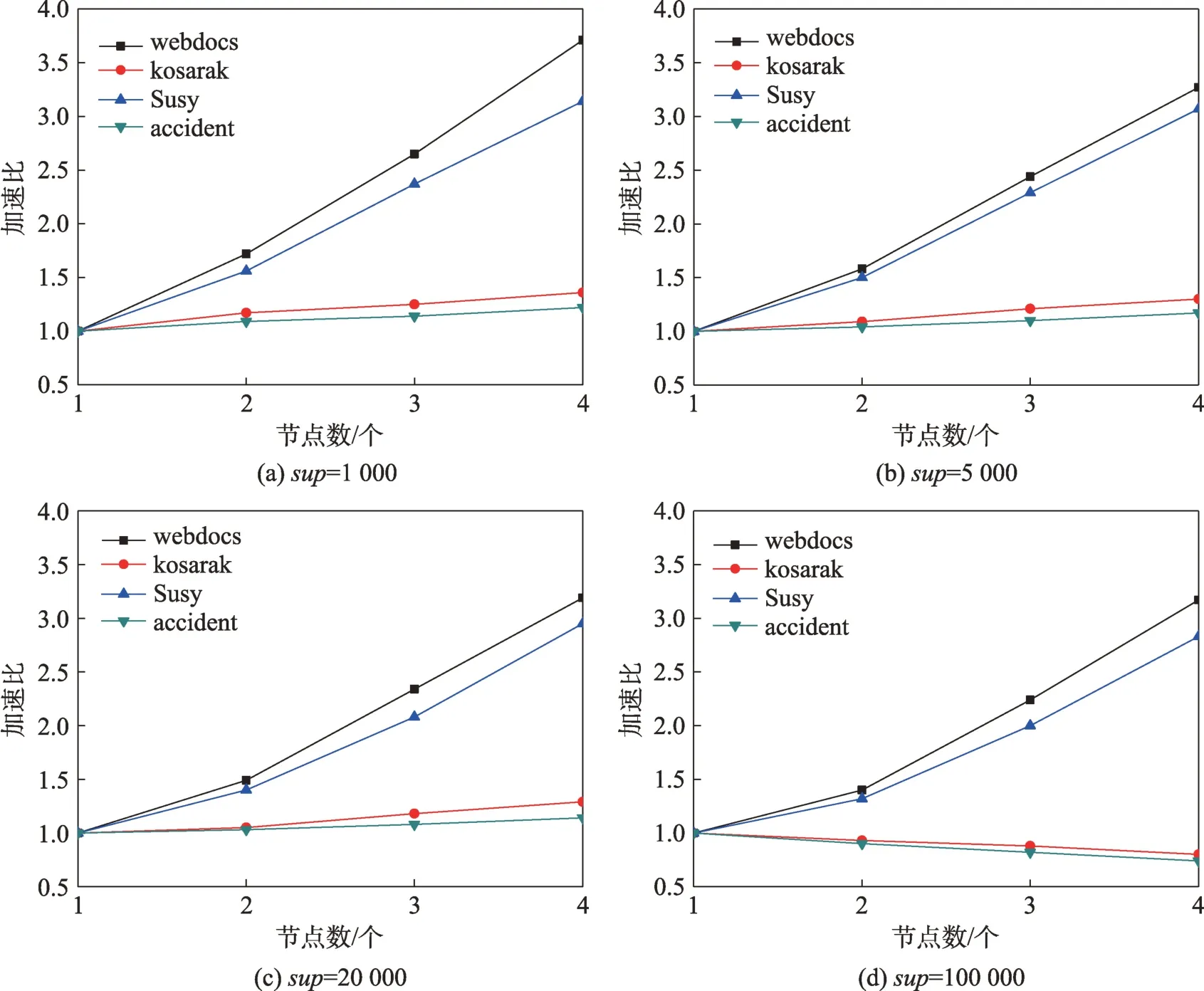
图6 算法在不同节点下的加速比Fig.6 Acceleration rate of algorithm on different computing nodes

为了分析并行挖掘频繁项集过程中均匀分组的必要性，本文选取最小支持度阈值为5 000 和100 000，在上述4 个实验数据集上进行对比实验。该实验比较了均匀分组和未均匀分组情况下算法运行时间分布情况，从而实现对GM-GS 策略的综合评估。其实验结果如图7 所示。

从图7 中可以看出，随着支持度的增加，采用GM-GS 策略在处理webdocs、Susy 两个规模较大的数据集时运行时间有较大减小，而在处理kosarak、accident 这样的小数据集时提升效果不太明显，这主要是由于小规模数据集使得在各个计算节点中构造的子PPC-Tree 树规模急剧减小，对于PPC-Tree 树的遍历所需时间相差不大。而在webdocs、Susy 等大数据集下，若未采用GM-GS 策略极易导致数据分组不均衡，各计算节点之间构造的子PPC-Tree 树规模以及遍历树所需要的时间相差较大。由此看出在并行挖掘频繁项集过程中GM-GS 策略是必要的。

图7 有无GM-GS 策略时算法运行时间的比较Fig.7 Comparison of algorithm running time with or without GM-GS strategy

3.5 HP-FIMBN 算法性能比较

为验证HP-FIMBN 算法的挖掘效果，本文在上述实验数据下进行了对比实验，根据算法的运行时间和内存使用量，分别与MRPrePost算法、LBPFP算法和MREclat算法进行性能比较。

在运行HP-FIMBN、MRPrePost 和LBPFP 算法时需要根据每个数据集的F-list 规模设置分组数，表12 给出四种数据集在不同支持度下F-list 数目的具体情况。根据F-list 以及数据集大小，对于Susy 数据集设置分组数为50 组，kosarak 和accident 数据集设置分组数为100组，webdocs 数据集设置分组数为1 000 组，实验结果如图8 所示。

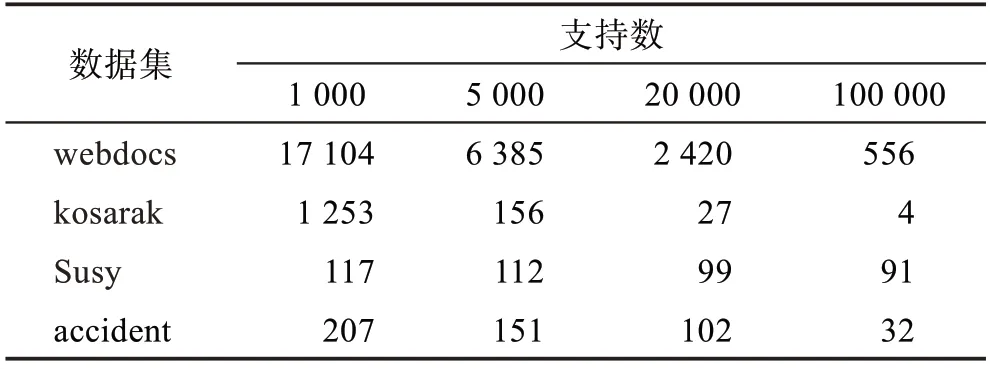
表12 不同支持度下四种数据集的F-list规模Table 12 F-list size of four data sets with different support degrees

从图8 中可以看出，相较于LBPFP 和MREclat 算法，HP-FIMBN 算法在每个数据集上的运行时间均有所下降。其中在kosarak 数据集上的运行时间降低幅度最大，分别降低了50.8%和69.74%；在webdocs数据集上降低的幅度最小，但也分别降低了20.06%和30.83%。这是由于HP-FIMBN 算法在并行挖掘频繁项集的过程中，将传统复杂的树遍历和迭代操作转化为简单的N-list 结构合并操作，极大降低了算法的运行时间。相反，在挖掘频繁项集时，MREclat 算法需要将水平数据集转成垂直数据集，然后采用类Apriori方法，通过对两个(-1)-项集的tid-list求交集来挖掘频繁-项集，该过程需要消耗大量的时间；同样，对于LBPFP 算法来说，在挖掘频繁项集时需要递归构建频繁项的FP-Tree，需要大量的计算资源。此外，可以发现HP-FIMBN 算法比最优的MRPrePost算法的挖掘效果都好，尤其在Susy 数据集上，HPFIMBN 算法的执行时间比MRPrePost 算法降低了19.97%。这主要是因为HP-FIMBN 算法采用GM-GS分组方法均匀地将频繁1 项集分配到各个节点中，在确保集群负载均衡的前提下降低了集群中子PPCTree 树的规模，由此减少先序、后序遍历PPC-Tree 树所需要的时间，加快生成本地2-项集的N-list结构；同时该算法在合并两个(-1)-项集的N-list 结构时，使用预先放弃策略可以提前得知该项集是否属于频繁项集，避免了合并过程中的无效计算，不仅提高了Nlist 结构的合并效率，而且极大降低了算法的运行时间。

图8 四种算法在不同数据集上的运行时间比较Fig.8 Comparison of running time of four algorithms on different data sets

然而从图8（b）、（d）中可以看出，在小规模数据集kosarak 和accident 上，相较于MRPrePost 算法，本文算法的实验提升不够显著。其中，一方面是由于小规模数据集的运算量不足以填充分布式集群；另一方面由于数据量较少，使得在各个计算节点中构造的PPC-Tree 子树规模急剧减小，导致-项集的Nlist 结构长度大幅降低，从而降低了预先放弃策略在合并两个N-list结构时所起到的作用。

由于LBPFP、MRPrePost 和HP-FIMBN 算法都对原始数据集进行了无损压缩，本文除了考察运行时间外，还统计了支持度为5 000、20 000 和100 000 下上述算法在集群中各个节点消耗的平均内存大小，实验结果如图9 所示。

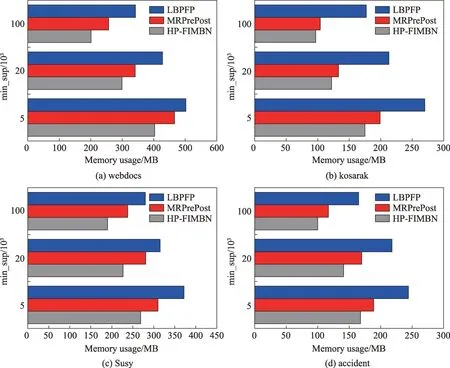
图9 不同算法在不同数据集上的内存使用量对比Fig.9 Comparison of memory usage of different algorithms on different data sets

从图9 可以看出，在4 个数据集上，HP-FIMBN 算法和MRPrePost 算法所使用的内存空间明显小于LBPFP 算法，这是由于HP-FIMBN 算法和MRPrePost算法在挖掘频繁项集时只需根据PPC-Tree 树生成频繁1-项集的N-list 结构，之后将PPC-Tree 树从内存中删除；而对于LBPFP 算法来说需要递归地构建条件模式子树，并且所有的条件子树都保留在内存中，需要消耗大量的内存空间。同时相较于MRPrePost 算法，HP-FIMBN 算法在4 个数据集上的内存使用量更少，尤其在Susy 数据集上，其内存使用量比MRPre-Post减少了19.4%。一方面，HP-FIMBN算法采用GMGS 分组方法在对频繁1 项集F-list 均匀分组的同时也减小各个计算节点中子PPC-Tree 树的规模；另一方面，在并行挖掘频繁项集的过程中，每个节点只需要将以当前组中项为后缀的频繁项集保存在内存中，大大降低了内存使用量。

4 总结

为解决传统频繁项集挖掘算法在大数据环境下的不足，本文提出了一种混合的并行频繁项集挖掘算法HP-FIMBN。首先，该算法充分考虑到集群负载对并行算法挖掘效率的影响，设计负载估计函数LE来计算出频繁1 项集中每项的负载量，并提出了一种基于贪心策略的分组方法GM-GS，将F-list 中的每一项根据其负载量进行均匀分组，既解决了数据划分中计算节点负载不均衡的问题，又降低了集群中各节点上子PPC-Tree 树的规模。其次，为了加快完成两个频繁项集N-list 结构的合并任务，提出了一种预先放弃策略EAS，该策略不仅能避免两个N-list 结构在合并过程中的无效计算，而且不需要遍历初始Nlist 结构就能得到最终的N-list，极大地提高了N-list结构的合并效率。最后，该算法采用集合枚举树作为搜索空间，并提出了一种超集等价剪枝策略（SES），来避免挖掘过程中的冗余搜索，生成最终的挖掘结果。与其他并行频繁项集挖掘算相比，该算法充分结合了水平型算法和垂直型算法的优点，利用其独特的方式来实现频繁项集的挖掘。同时为了验证HP-FIMBN 算法的挖掘性能，本文在4 个数据集Susy、webdocs、kosarak 和accident上对HP-FIMBN、MRPrePost、LBPFP 和MREclat 四种算法进行对比分析，实验结果表明相比于其他几种算法，HP-FIMBN算法在运行时间和内存使用量上都具有明显的优势。