面向多分类自闭症辅助诊断的标记分布学习

章枫叶欣，王 骏，贾修一，潘 祥，邓赵红，施 俊，王士同

1.江南大学 人工智能与计算机学院，江苏 无锡214122

2.上海大学 通信与信息工程学院，上海200444

3.南京理工大学 计算机科学与工程学院，南京210094

自闭症谱性障碍（autism spectrum disorder，ASD）是一系列复杂的神经发展障碍性疾病，其临床表现主要为社会交往障碍、言语交流障碍和动作刻板重复等。美国疾控中心数据统计显示，美国儿童的自闭症患病率高达1∶59。这表明自闭症已经成为一个相当严重的健康问题，迫切需要开发一种有效的方法进行及时诊断。但是由于自闭症的生理原因并不明朗，医学诊断只能根据患者的症状及反馈、定性/定量的检测信息、医师的个人经验等，具有很大的不确定性。因此，借助计算机进行自闭症的辅助诊断具有重要的意义。

研究表明，自闭症谱系障碍与患者的脑功能异常有关，而通过使用血氧依赖水平反映患者在静息状态下脑部代谢活动等功能性变化的静息态功能性核磁共振图像（resting-state functional magnetic resonance imaging，rs-fMRI）已成为量化大脑神经活动的有力工具，逐渐成为ASD 等脑部疾病研究的重要手段之一。以此为诊断依据，研究者们提出了多种借助计算机的自闭症辅助诊断算法。如，Chen 等使用高阶功能性连接矩阵进行自闭症的辅助诊断，Aggarwal等提出多元图学习进行自闭症的辅助诊断，Heinsfeld 等通过深度学习探求脑区之间的相关性进行自闭症的辅助诊断等。但是这些方法仅能处理二分类问题，而在临床中，自闭症谱性障碍包括若干与发育障碍相关的疾病，如自闭症（autism）、亚斯伯格症候群（Asperger's disorder）和无特异性的普遍发育障碍（pervasive developmental disorder not otherwise specified，PDD-NOS）等。已有的大多数自闭症辅助诊断模型仅能解决二分类问题，无法同时区别ASD 的若干相关疾病。此外，这些方法也没有对标记噪声进行有针对性的处理。

标记噪声是多分类ASD 辅助诊断涉及的一个挑战，对分类器性能有着严重的不良影响。标记噪声指训练样本的目标标记和对应实例的真实标记的偏差。标记噪声的产生有多方面的因素，例如：标注过程中具有主观性，待标记样本本身可辨识度低，通信/编码问题等。在自闭症诊断场景中，标记噪声普遍存在。诊断过程中的主观性，诊断标准的不统一以及ASD 各子类的界限模糊这些特点造成了标记噪声。

高维特征下的类不平衡问题是多分类ASD 辅助诊断涉及的另一个挑战。通常用于ASD 辅助诊断的神经影像数据动辄成百上千个特征，加之训练样本数目非常有限，在进行分类器训练时容易导致过拟合问题。而且用于构造ASD 分类器的样本存在类别不平衡问题，导致分类预测结果往往偏向多数类。

针对上述问题，本文提出了一种代价敏感的标记分布支持向量回归学习来进行ASD 的辅助诊断。首先，多分类ASD 辅助诊断面临着标记噪声问题，而标记分布独有的标记形式，通过不同标记对于同一样本的描述度，能够更好地克服标记噪声对分类器的影响，从而精确表达标记之间的相关程度。这就使学习过程蕴含了更加丰富的语义信息，可以更好地区分多个标记的相对重要性差异，对ASD 辅助诊断中的标记噪声问题有较好的针对性。同时，支持向量回归引入了核方法，通过核方法的非线性映射，使得原始输入空间中线性不可分的数据可以映射入一个线性可分的特征空间，提供更多的可鉴别信息。最后，为了克服类别不平衡问题，引入了代价敏感机制，通过引入现实中存在的不同类别的误判代价的不平衡性，使得算法能在一定程度上适应实际应用的需求，较公平地对待少数类和多数类。

1 相关工作

1.1 标记分布学习

标记分布学习（label distribution learning，LDL）是近几年兴起的一种机器学习方法，它是在单标记和多标记学习的基础之上，引入了标记分布的概念。在多标记的场景下，一个样本如果与多个标记相关，这些标记对于该样本的重要程度一般会有所区别，标记分布就是描述不同标记对于同一样本的重要程度的标记形式。标记分布学习就是以标记分布为学习目标的一种机器学习方法，已经被应用于诸多领域。例如，Gao 等提出了结合卷积神经网络和标记分布学习的深度标记学习（deep label distribution learning）算法通过人脸估计年龄，Zhou 等提出了基于普鲁契克情感色轮（Plutchik's wheel of emotions）的情感分布学习（emotion distribution learning）算法来从文本中自动识别用户的情绪状态，Geng等提出了基于多变量标记分布（multivariate label distribution）的算法实现头部姿势检测。但是用于脑疾病的辅助诊断目前尚未见报导。

1.2 标记增强

标记分布学习要求训练数据包含标记分布信息。然而，现实生活中人们往往以单标记或多标记的形式来标记样本，使得难以直接得到标记分布信息。尽管如此，这些数据的标签中仍然包含标记分布的相关信息。标记增强通过隐含在不同样本标记之间的相关性，强化样本的监督信息，进而在标记分布学习中获得更好的效果。例如，Xu 等提出了标记增强作为标记分布学习的辅助算法，用于挖掘训练集中的蕴含的标记重要性信息，将原始的逻辑标记提升为标记分布，辅助标记分布学习。Shao 等提出了标记增强多标记学习（label enhanced multi-label learning）从逻辑标记中重建潜在的标记重要性信息来改善标记分布学习的性能。

2 面向ASD 辅助诊断的代价敏感的标记分布学习

2.1 符号表示

2.2 方法流程

本文提出的面向多分类自闭症辅助诊断的标记分布学习算法，其流程如图1 所示。首先，对rs-fMRI图像进行预处理，在此基础上构建功能连接矩阵，并基于功能连接矩阵得到每个样本的功能连接特征向量。同时，结合逻辑标记数据和功能连接特征进行标记增强，获得样本的标记分布形式。最后，进行基于代价敏感的标记分布学习建模，从而得到面向自闭症辅助诊断的多分类模型。

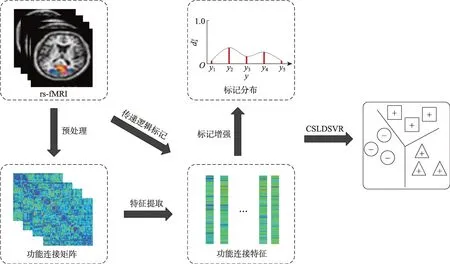
图1 代价敏感的标记分布支持向量回归的流程图Fig.1 Flowchart of cost sensitive label distribution support vector regression

2.3 标记分布自闭症辅助诊断数据集的获取

标记分布学习通过引入描述度来刻画每个标记和样本的相关程度，因此它可以从数据中得到比多标记更加丰富的语义信息，更加准确地表述同一个样本的多个标记的相对重要性差异。然而，标记分布学习的基本要求是要有标记分布的数据集，这一点在现实中往往很难满足要求。可以通过标记增强方法对给定的多标记形式样本进行转化得到标记分布形式数据。采用基于FCM（fuzzy C-means）和模糊运算的标记增强方法，基本思路如下：

（1）利用FCM 把个样本分为个模糊聚类，并求每个聚类的中心，使得所有训练样本到聚类中心的加权距离之和最小，式（1）列出了具体的加权距离公式。

（2）构造标记和聚类之间的关联矩阵，矩阵中的元素即代表了标记和聚类的关联度，关联矩阵的计算方法如式（2）。

式中，A为矩阵的第行，A即第个类的样本的隶属度向量之和，行归一化之后，关联矩阵可以视作一个聚类和标记的模糊关系矩阵。

（3）根据模糊逻辑推理机制，将关联矩阵和隶属度进行模糊合成运算，得到样本对标记的隶属度，归一化后，即为标记分布。

基于FCM 和模糊运算的标记增强引入聚类分析作为桥梁，通过样本对聚类的隶属度和聚类对标记的隶属度这两者之间的复合运算，得到样本对标记的隶属度，即标记分布。在这一过程中，通过模糊聚类挖掘样本空间的拓扑关系，并且通过关联矩阵将这种关系投影到标记空间，从而使得简单的逻辑标记产生了更丰富的语义信息，转变为标记分布。

2.4 代价敏感的标记分布支持向量回归学习

面向ASD 辅助诊断进行标记分布学习建模，需要重点考虑以下两个关键问题：首先，ASD 数据样本的各类分布不平衡。研究表明，在有监督的机器学习任务中，类别不平衡会对训练产生不利影响。它既影响训练阶段的收敛，也影响测试集上模型的泛化能力。因此，本文在标记分布支持向量回归的基础上引入了代价敏感机制，从而平衡多数类和少数类对目标函数的影响。其次，ASD 数据集大多是多分类数据，而指导标记分布学习训练的数据应该是标记分布的数据。为此，引入了标记增强，将每个训练样本的标记转化为标记分布。标记增强的过程在2.3 节中有简要描述。

假定样本对应的标记分布可以由样本在特征空间的投影线性表示：

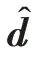
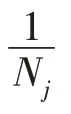
(u)是关于w、b的凸函数。

证明式（5）是凸函数，即证明(u) 关于w、b的二阶导数恒大于等于0：

其中，(w,(x))是关于w、(x)的函数。显然式（8）恒大于等于0，同理可证(u)关于b非负，定理得证。

本文使用拟牛顿迭代法（iterative quasi-Newton method）优化式（4）。首先，本文将式（4）的第二部分进行泰勒级数展开，取其线性部分作为近似值，在第次迭代中，近似值如下：

其中，是一个与,无关的常量。式（10）分别对w、b求偏导，并令偏导数的值为0，可以得到公式：

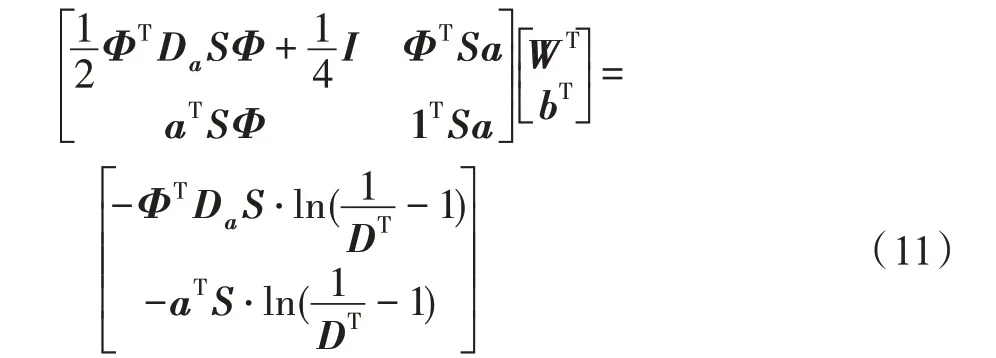
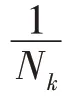
其中，K=(x,x)=(x)(x)，K为矩阵的第行第列的元素值，(x,x)即核函数。至此，将、代入式（3），预测函数可以更新为：

即可从样本的输入特征空间计算得相应的标记分布。标记分布的结果即ASD 及其子类对于同一样本的重要程度，取最大可能标记作为结果：

CSLDSVR

输入：自闭症数据，标记分布，权重系数，核函数类型，不敏感区大小，核带宽。

输出：预测模型、。

3 实验结果和分析

3.1 评估指标

本文同时使用标记分布的评估指标和多分类任务的评估指标进行算法评估。所有评估指标及计算公式如表1 所示，前六种为标记分布学习的评估指标，后两种为多分类任务的评估指标。指标名后带有“↑”表示数值越大，算法效果越好；带有“↓”，表示数值越小，算法效果越好。

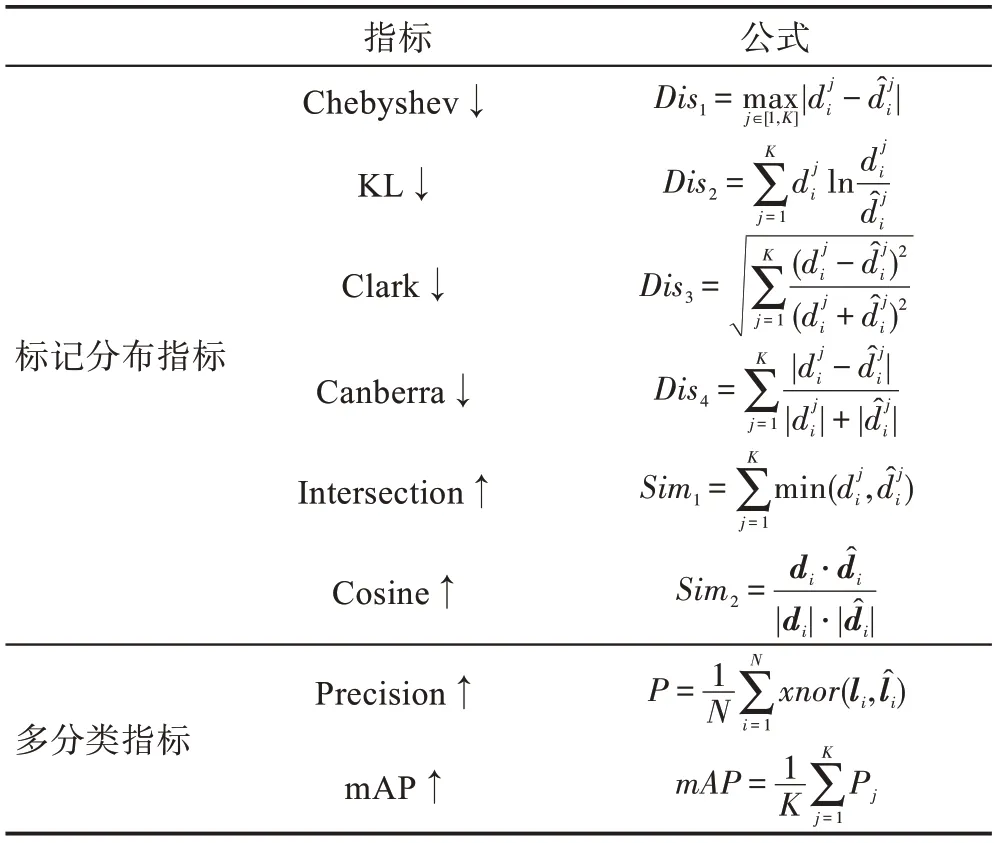
表1 评估指标Table 1 Evaluation measures

表1 中，P为第类的Precision，为异或计算，代表距离（Distance），代表相似度（Similarity），代表宏平均正确率（macro-averaging precision）。

3.2 数据集及预处理

本文使用的所有rs-fMRI 数据集均来自ABIDE网 站（Autism Brain Imaging Data Exchange，http://fcon_1000.projects.nitrc.org/indi/abide/）。表2 给出各数据集中各类样本的组成情况。以NYU（New York University）数据集为例，NYU 数据集数据采集机构为纽约大学。采集过程中，被试者始终保持静息状态，不执行任何动作。具体参数如表2 所示。

表2 数据集的统计信息Table 2 Statistics of datasets

表2 中，UM 代表密歇根大学，KKI代表肯尼迪克里格研究所，Leuven 代表鲁汶大学，UCLA 代表加利福尼亚大学洛杉矶分校。

虽然大脑各脑区在空间上相互隔离，但它们之间的神经活动相互影响。本文使用脑区之间的脑功能连接矩阵作为分类特征。功能连接矩阵的计算步骤（即预处理步骤）如下：

（1）根据静息态功能磁共振成像数据，使用DPARSF（data processing assistant for resting-state fMRI）工具提取出各脑区的平均时间序列信号，计算脑区之间的Pearson 系数，得到功能连接矩阵。

（2）将功能连接矩阵的每一行作为各脑区的特征描述，取功能连接矩阵的上三角阵，按行串联，得到对应的特征向量。

3.3 对比算法

将提出的CSLDSVR 方法和6 个现有LDL 算法以及两个多分类算法进行对比。两个多分类算法为决策树（decision tree）和最近邻（-nearest neighbor，NN），这两种算法均为经典的多分类算法。6 个现有LDL 算法为：PT-SVM、PT-BAYES、AA-NN、AA-BP（back propagation）、SA-IIS（improved iterative scaling）、LDSVR，其中，“PT”表示问题转化（problem transformation），“AA”表示算法改造（algorithm adaptation），“SA”表示专用算法（specialized algorithm）。对比算法的具体说明如表3 所示。

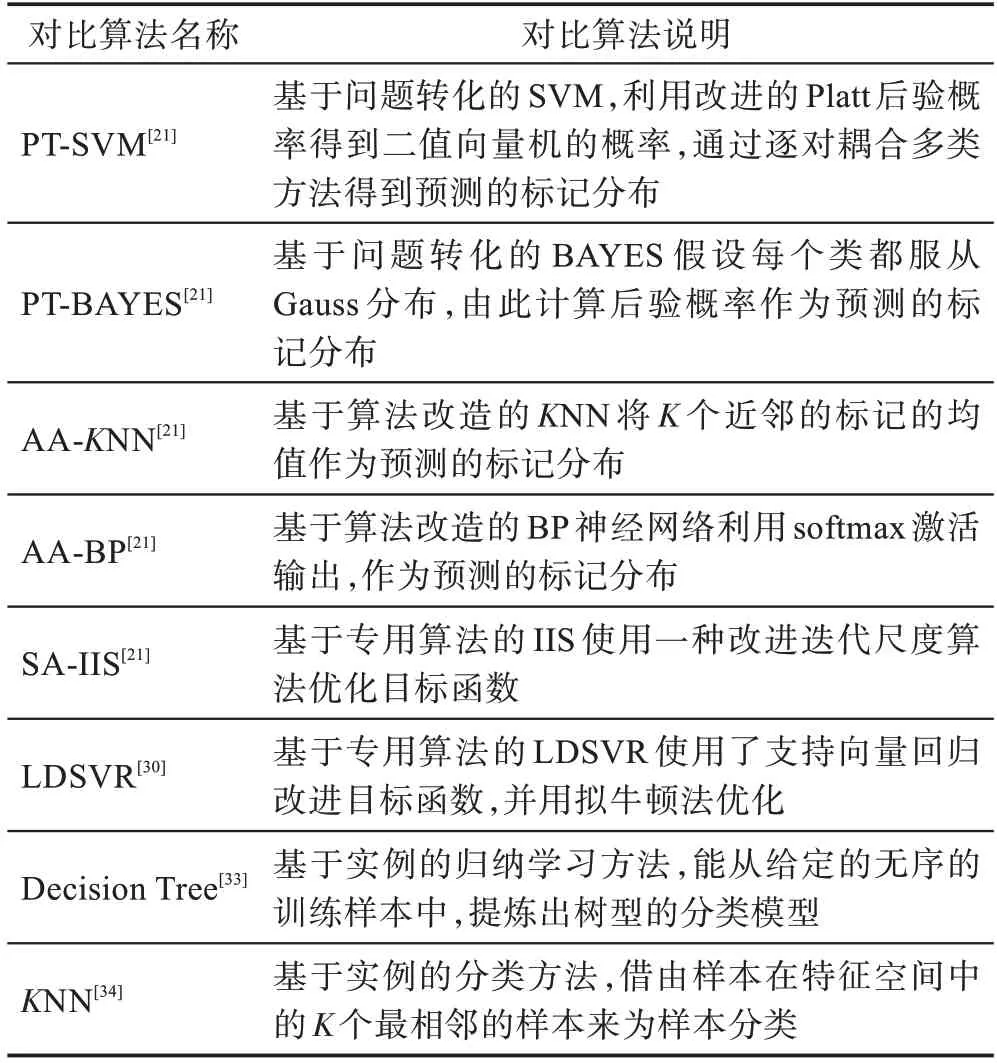
表3 对比算法Table 3 Comparison algorithms

本文提出的CSLDSVR 算法有4 个参数，即权重系数、核函数的类型、不敏感区大小、高斯核的核带宽。参数具体的范围如表4 所示。使用十折交叉验证来计算结果。具体操作步骤如下：将数据集随机划分为10 等份，在每一折交叉验证中，取1 份作为测试集，剩下9 份作为训练集。重复上述过程10次，取10 次结果的均值作为评价指标。

表4 参数范围Table 4 Range of parameters

3.4 标记分布算法对比

表5 汇总了6 个标记分布学习算法和CSLDSVR在5 个不同的数据集上的实验结果，实验结果以均值±标准差的形式记录。其中，加粗的为每一个指标在当前数据集上不同方法中的最佳数值。显然可见，在和标记分布学习算法的对比中，CSLDSVR 在多数情况下都表现出了优异的效果，在UM、UCLA、KKI 数据集上更为明显。在标记分布的指标中，KL散度是描述两个分布的差异的指标，而且作为对比的LDL 算法都是以KL 散度作为目标函数的，CSLDSVR 的预测结果的KL 散度可以做到最小，说明新算法预测的标记分布总体上和真实数据分布最相近，优于对比算法。

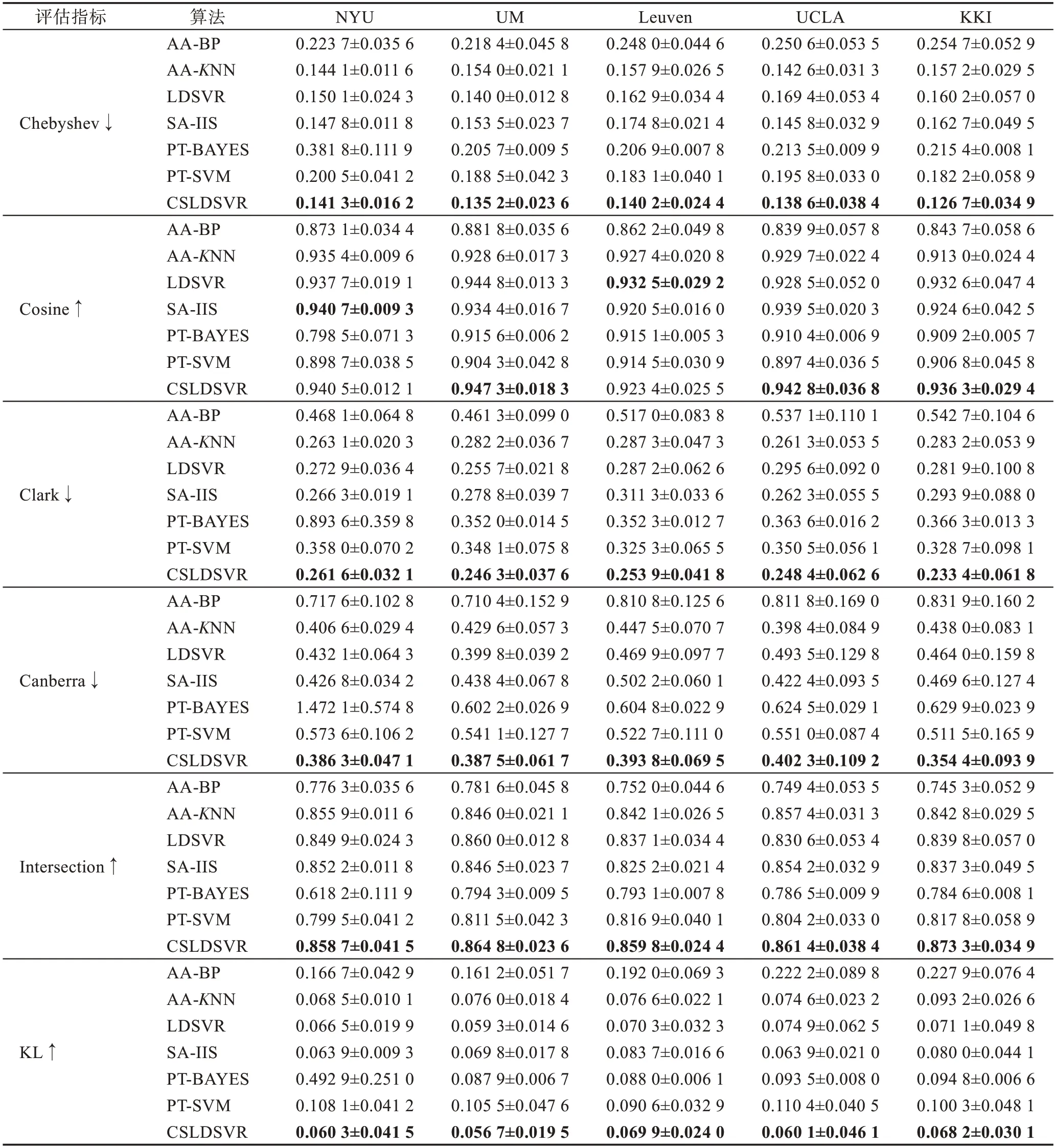
表5 CSLDSVR 和标记分布算法的性能比较Table 5 Performance comparison of CSLDSVR and LDL algorithms

图2 汇总了CSLDSVR 和标记分布算法多分类指标Precision 和mAP 的结果，在最重要的两个多分类指标上，CSLDSVR 都表现较佳。有些算法正确率高，宏平均却很低，这是因为这些算法没有考虑类别不平衡问题，模型分类偏向多数类。CSLDSVR 使用了核技巧，可以在更具有鉴别能力的特征空间中解决问题，而且CSLDSVR 考虑了每个类的大小，从而有效解决了因类别不平衡而带来的问题。

图2 CSLDSVR 和标记分布算法的分类效果对比Fig.2 Comparison of classification performance of CSLDSVR and label distribution algorithms

为了验证代价敏感机制对性能的提升，将本文算法与没有代价敏感机制的LDSVR 进行对比。如表5 所示，在多数情况下，本文算法CSLDSVR 的学习效果较好；此外，结果的标准差基本都维持在一个较低的水准，即算法的稳定性有所提高。而LDSVR未引入代价敏感机制，算法所得结果的标准差较大且波动，例如在UCLA 和KKI的Canberra 指标标准差都超过了0.1。

3.5 多分类对比实验

表6 CSLDSVR 和多分类算法的性能比较Table 6 Performance comparison of CSLDSVR and multi-classification algorithms

3.6 参数敏感性分析

本节研究参数的变化对算法CSLDSVR 性能的影响，图3 给出了在5 个不同数据集上，参数、取不同值时，评估指标Precision 和KL 散度的变化。对照研究同一参数不同指标的两张图，例如图3（a）和图3（c），可以发现同一个数据集的曲线走势基本是相反的，Precision 取最大值的点一般KL 散度也恰好为最小值，这也与前文对KL 散度的分析相照应，说明在KL 散度较小时，两者的标记分布更为相似，分类的结果也更加准确。

图3 参数C、ε 在5 个数据集上的敏感度分析Fig.3 Sensitivity analysis of parameters C and ε on 5 datasets

发现对于不同数据集，取到最优解的参数值并不相同，这也表明了在自闭症诊断中，不同数据中心的数据分布不同，构建模型的参数也应该不同。而且发现样本数量越少的数据集，结果对参数的变化越敏感，例如仅有48 个样本的KKI 数据集，在参数值变化时波动最大。

由此可见，CSLDSVR 算法的参数应针对数据集的特点，设定相应的参数值构建模型，在参数设置合理的情况下，CSLDSVR 可以克服自闭症数据集的高维度和类别不平衡问题，取得更好的分类效果。

4 结论和展望

ASD 患者的脑功能异于正常人，而rs-fMRI 是反映大脑活动的有效工具，本文基于从rs-fMRI 中提取的功能连接特征，提出了一种代价敏感的标记分布支持向量回归的ASD 辅助诊断方法。标记分布学习的引入，克服了基于多分类的ASD 辅助诊断的标记噪声问题。而且新的方法在标记分布支持向量回归的方法基础上，引入了类别平衡，平衡了多数类和少数类对目标函数的影响。新的方法克服了多数类和少数类对结果的影响的不平衡性，可以有效解决ASD 诊断中的不平衡数据问题，但是改进模型还是一定程度地偏向多数类，要进一步地改善不平衡数据问题，可以尝试改进数据的采样方法或使用合成少数类样本方法等，这值得进一步的研究；同时，损失函数可以改用更复杂的距离度量方式，欧氏距离平等对待每个特征，因此能够体现个体特征数值上的绝对差异。但引入相对高级的距离也有其必要性，不过这需要更多的先验知识。目前没有使用更多的先验知识，因此使用欧式距离。其他高级距离有其优势，在今后的研究中将进一步改进本文工作。