一致性约束的半监督多视图分类

刘 宇，孟 敏，武继刚

广东工业大学 计算机学院，广州510006

随着科技不断发展，获取数据的方式呈现着多元化的趋势，从而使得这类数据可以由多种数据特征表示。例如，一个图像可以由多种不同的特征来描述，如方向梯度直方图特征（histogram of oriented gradients，HOG）、尺度不变特征变换特征（scaleinvariant feature transform，SIFT）、局部二值模式特征（local binary pattern，LBP）等；对于一个网页，它可以由网站网址、网页中的文本信息以及网站名称等特征来描述；在生物学数据中，每个人类基因可以通过基因表达、阵列比较基因组杂交（ACGH）、单核苷酸多态性（SNP）和甲基化来测量。对于这类可以由不同特征集来共同表示的数据，称为多视图数据。在过去几十年里，单视图算法在降维、分类、聚类以及回归领域上都取得了巨大的进展，但由于不同特征视图的有效组合能够很好地提高算法的准确性，近年来多视图算法成为了广大学者的研究热点。

基于全局结构和局部流形结构的特征投影能够提取有效的判别信息来对原始数据空间进行降维，并结合低秩表示与稀疏学习方法可以提高算法的鲁棒性，这些方法同时也被广泛地应用于多视图学习。例如，低秩公共子空间多视图学习（low-rank common subspace for multi-view learning，LRCS）方法，通过学习一个共同的低秩线性投影来减少不同视图之间的语义差距。为了更多地保留每个类中所包含的信息，Ding 等考虑了类结构与视图结构并通过成对的低秩分解来进行求解。Kan 等通过最大化类间间距以及最小化类内差异来学习投影矩阵进行人脸识别。基于深度矩阵分解多视图聚类（multi-view clustering via deep matrix factorization，MVC）的方法，运用了半非负矩阵因式分解的方法来学习多视图数据的层次语义，并通过保留原始数据固有的几何结构来进行多视图聚类。通过对正则化函数施加范数和迹范数约束，Lu 等提出了一种新颖的凸多视图低秩稀疏回归算法来进行聚类和特征选择。Zhong 等通过考虑多个视图的互补性和每个视图的特殊性，提出了基于判别稀疏进行加权特征选择的多视图学习方法。通常，这些算法都需要大量的标签数据进行训练。在实际应用中，收集到的数据经常含有少量的标签数据和大量的无标签数据，并且对大量无标签的数据进行标记会消耗大量的人力资源。因此，半监督学习得到了有效的发展。

半监督学习方法能够同时使用标签信息和无标签数据中的空间结构信息，自动地为无标签数据进行标记。基于此特性，半监督学习方法被广泛地应用于多视图的分类与聚类。自适应多模态的半监督分类算法，将每种类型的特征视为一种模式，学习了不同模式的共享类指标矩阵和权重。通过利用标签数据的判别信息和原始数据的流形结构，Han 等提出了半监督多视图流形判别完整空间学习。潜在的多视图半监督分类（latent multi-view semi-supervised classification，LMSCC）方法将潜在表示学习、图构造和标签传播集成到一个统一的框架中，使得每个子任务都能得到优化。Liu 等通过对模块化度量进行分析，设计了一种边缘函数自动地为每个属性分配理想的权重，并将拓扑结合到图形聚类中。然而这些算法都没有考虑到每个视图之间存在着数据结构的一致性，从而使得多视图算法的性能并不是很理想。因此，基于视图结构一致性的算法引起了学者们的研究。Zhang 等用拉普拉斯（Laplacian）和黑赛（Hessian）图组成的群图流形正则化器，并结合具有全局标签一致性的半监督学习，提出了全局标签一致分类器。Wang 等通过引入位置感知独占项（position-aware exclusivity term）来获取不同表示之间的互补信息，同时使用一致性约束来进行互补表示。Tao等基于视图之间的联系和不同视图包含的信息，提出了多视图协作表示分类方法。然而这些算法仍然存在以下几个问题：（1）对不同视图一致性约束的度量较为单一，没有考虑到在不同的空间中每个视图的数据结构存在着联系。（2）部分半监督分类算法仅仅局限于对空间结构的保持，忽略了对原始数据进行特征提取和相似矩阵的F 范数约束，从而无法避免噪声以及其他不相关特征的影响。（3）没有考虑到不同视图包含特征信息量的差异性，无法对每个特征视图进行合理的加权。

针对以上问题，本文提出了基于一致性约束的半监督多视图分类（semi-supervised multi-view classification via consistency constraint，SMCC）算法。该算法同时保持了不同视图之间的一致性结构与每个视图的局部流形结构，并对相似矩阵进行F 范数约束，其主要贡献有以下几个方面：不仅仅局限于欧式空间距离的度量，还结合了希尔伯特空间的度量，并基于希尔伯特-施密特独立性准则保持了不同视图之间数据结构的一致性；通过对原始数据进行保留局部流形结构的特征投影提取有效的判别特征，以及对相似矩阵的F 范数约束提高了算法的鲁棒性；根据不同视图包含的不同特征信息量，自适应地赋予不同视图相应的权重；基于线性交替方向乘子方法（linear alternative direction method with adaptive penalty，LADM），对提出的算法设计了有效的求解方法；通过大量实验结果证明，本文算法能够捕获多视图数据中更多的有效判别信息，提高了算法的准确性。

1 相关工作

特征投影通过提取原始数据的有效判别特征不仅能降低计算成本，而且能够提高算法的准确性。因此，相关学者对多视图特征投影方法进行了广泛的研究。与大多数直接在每个视图中分别进行特征投影不同，潜在的多视图子空间聚类（latent multiview subspace clustering，LMSC）方法基于每个视图都起源于一个潜在表示来对原始数据空间进行重构，再利用不同视图之间的互补性进行子空间聚类。为了缩小多个视图之间的语义差异，Ding 等将多个视图特定投影转换为共享的多视图低秩投影，并将类内数据耦合到不同的视图中，使所学习的集体子空间更具鉴别性。然而在实际应用中，获取的原始数据通常只含有少量的标签，这使得上述算法无法得到足够的标签数据进行训练，从而导致算法的性能较低。因此，为了充分利用未标记数据中所包含的判别信息，学者们对半监督学习算法进行了广泛的研究。

典型的半监督学习算法包括基于高斯场和谐波函数的半监督学习方法与FME（flexible manifold embedding）算法。通过结合多视图学习与半监督学习算法，Nie 等提出了多视图聚类与半监督分类的框架算法（parameter-free auto-weighted multiple graph learning，AMGL），其算法能够不引入附加参数即可对每个视图自适应地赋予相应的权重。面向图聚类和半监督分类的自适应权重多视图学习（autoweighted multi-view learning for image clustering and semi-supervised classification，MLAN）方法，通过考虑原始数据中存在的噪音以及空间局部流形结构，有效提高算法的鲁棒性，并且在合理的秩约束下，得到的最优图可以直接划分为特定的簇，有效地提高了聚类与半监督分类的性能。基于自适应回归的可增强多视图半监督分类（scalable multi-view semi-supervised classification via adaptive regression，MVAR）方法，对每个视图都采用基于回归矩阵范数的损失函数，并将最终的目标函数表示为所有损失函数的线性加权组合。然而，上述半监督分类算法对数据局部结构的保持仅仅在单一的欧式空间中进行度量，且都忽视了不同视图之间的数据存在着潜在的一致性结构。而本文算法基于多度量学习，考虑了希尔伯特空间中的一致性结构，构造了更稳健、更鲁棒的判别性投影，有效地提高了分类精度。通过考虑多视图数据在不同视图的多个度量中存在固定联系，Zhang 等基于Fisher 判别分析与希尔伯特-施密特正交准则提出了Fisher-MML（Fisher-HSIC multi-view metric learning）多视图度量学习方法，但此方法缺少对局部结构的保持、每个视图的合理加权以及忽视了未标记数据的结构信息与噪音的污染，从而使得算法在多视图分类中准确率较低。而本文提出的SMCC 算法基于半监督学习，保留了欧式空间中的局部结构以及对表示矩阵进行了F 范数约束，有效地提高了算法对噪音的鲁棒性，并自适应地为不同视图赋予了相应的权值，提高了算法的准确性，弥补了上述算法的缺陷。

2 本文算法框架

本章主要内容是对基于一致性约束的半监督多视图分类方法进行详细的介绍，并基于交替迭代（LADM）方法对所提出的算法进行优化求解。为了便于理解，在优化过程中本文主要对多视图数据=[,,…,X]∈R中的第个视图X进行分析，其他视图与此类似。考虑到本文算法使用的变量较多，因此首先在表1 中对主要使用的符号以及变量进行必要的注释。

表1 符号解释Table 1 Symbolic interpretation

2.1 SMCC 算法

通常数据中的局部流形结构信息比全局结构信息更重要。为了能够使原始数据X=[,,…,x]∈R在降维后保持空间局部结构，得到表达式如下：

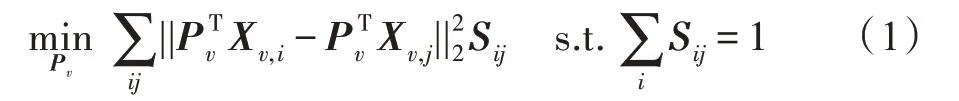
其中，X∈R表示第视图的第列向量，P=[,,…,p]∈R表示第视图投影矩阵，表示相似矩阵，其初始化定义为：

考虑在实际应用中数据存在噪声或异常值，本文对相似矩阵进行F 范数约束并限定S取值范围在[0,1]，用公式描述为：

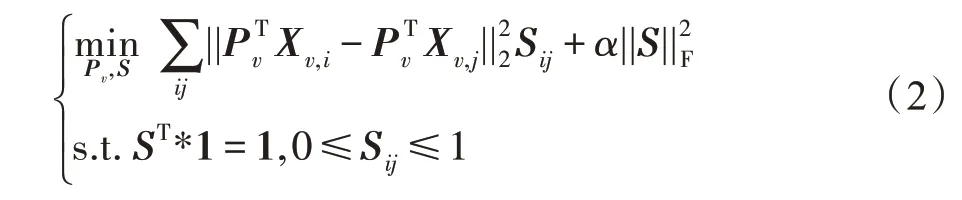
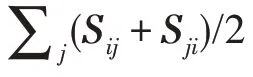
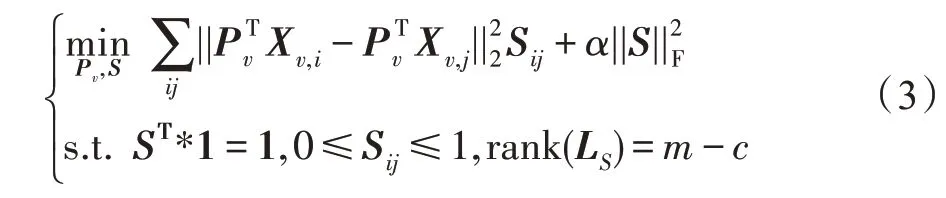
以上公式是基于欧式空间来度量变量之间的差异以及保留数据的空间结构信息，为了在不同的空间中挖掘数据包含的判别信息，本文考虑了在希尔伯特空间对多视图数据进行度量。基于希尔伯特-施密特独立性准则（Hilbert-Schmidt independence criteria，HSIC）能有效地挖掘多视图数据中的互补信息，使得多个视图的数据能够在希尔伯特空间上保持结构一致。一般而言，典型的HSIC 算法能够定义为：

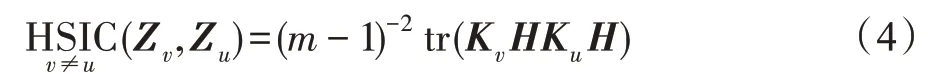
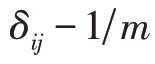
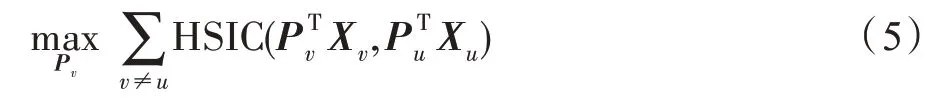
由于每个特征视图包含的信息量有所差异，引入权重参数对不同的视图进行权衡。为了规范相似矩阵的表示以及防止过拟合，将投影矩阵约束为正交矩阵，并结合式（3）与式（5）可得到目标函数表达如下所示：

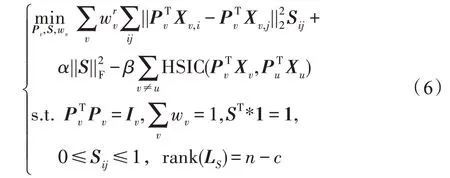
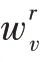
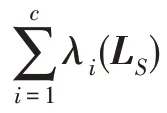
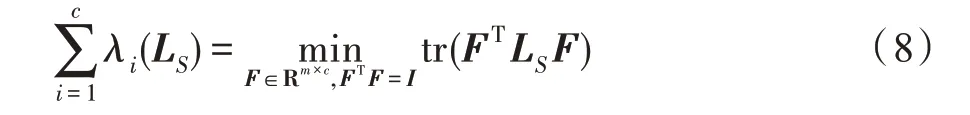
通过式（8），则上述目标函数（6）可转化为：

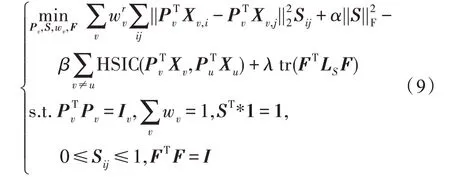
其中，表示预测标签矩阵，表示超参数，tr(∗)表示迹函数。本文算法整体流程框架如图1 所示。

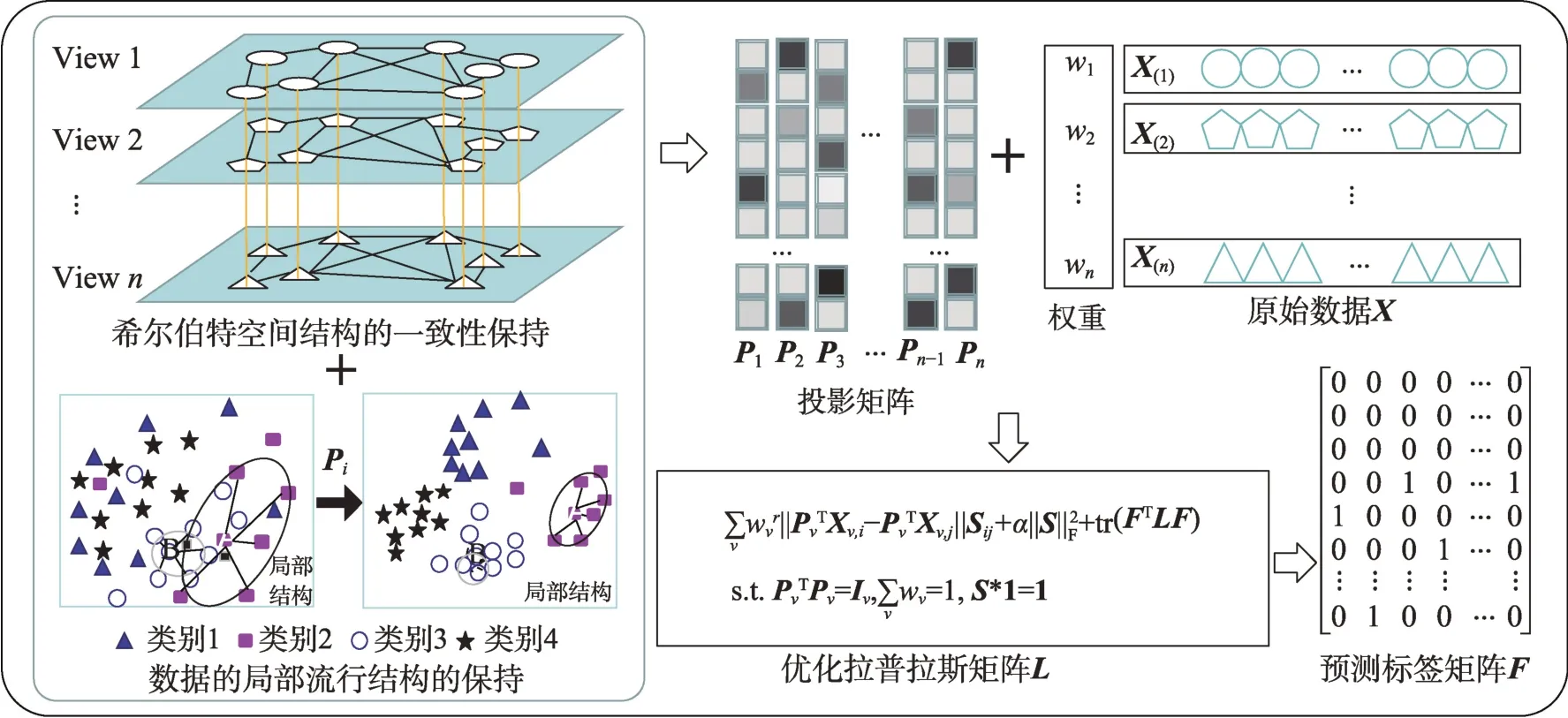
图1 算法框架流程图Fig.1 Flowchart of algorithm framework

2.2 优化

由于基于一致性约束的半监督多视图分类方法的目标函数属于多变量优化问题，本文基于LADM方法对各个变量进行交替迭代更新。求解本文算法的基本思想是对某个变量进行优化时，固定其他变量。具体更新步骤如下所示：

（更新P）固定变量、w、，则关于变量P的优化函数可表示为：

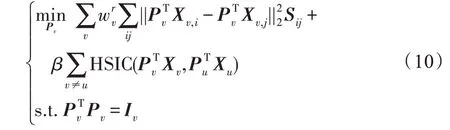
经过代数转换可得：

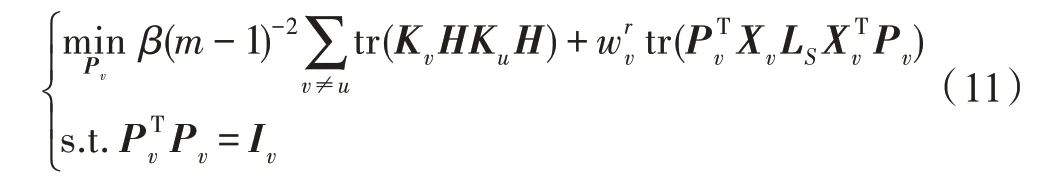
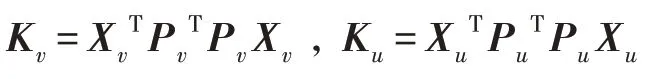
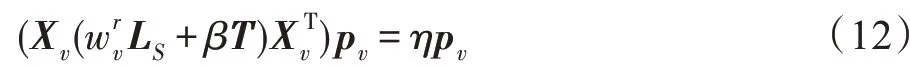
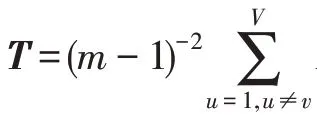
（更新w）固定变量、P、，则关于变量w的优化函数可表示为：

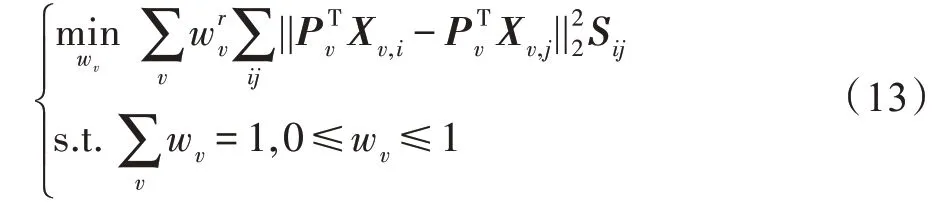
进而可以得到式（13）的拉格朗日表达式为：

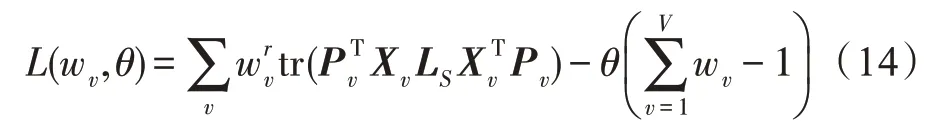
其中，为拉格朗日乘子。将(w,)函数相对于与w的偏导数分别等于0，则可得表达式：

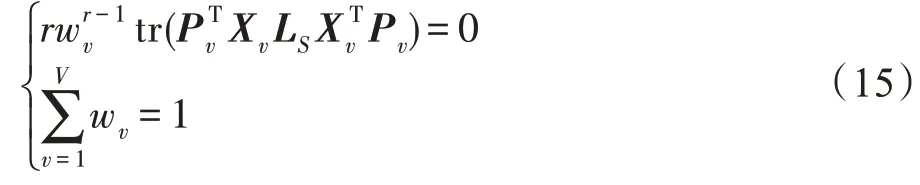
因此可以得到关于w的表达式为：

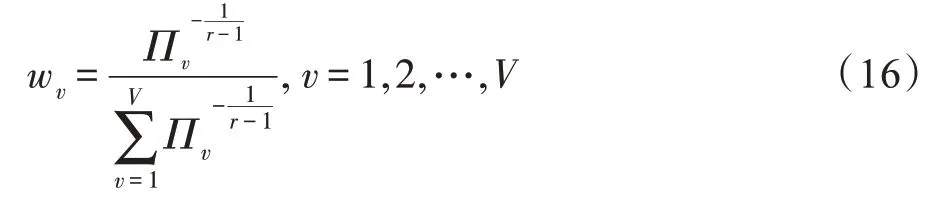
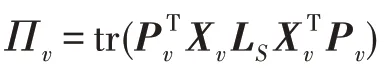
（更新）固定变量w、P、，则关于变量的优化函数可表示为：

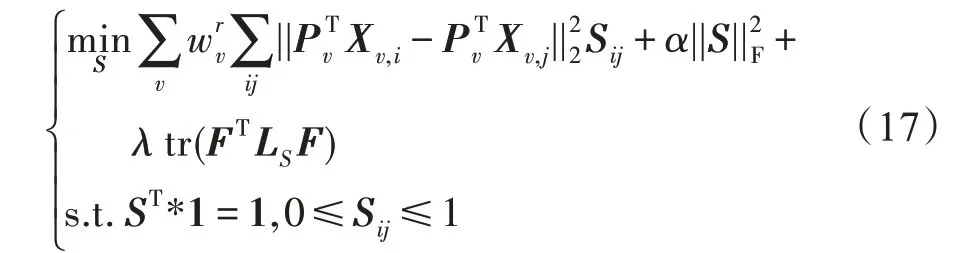
对于预测标签矩阵=[,,…,f]∈R在谱聚类算法中，有以下表达：

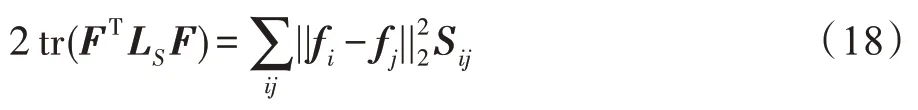
由于在式（17）中对于不同的都相互独立，对=[,,…,S]中任意项S优化可表示为：

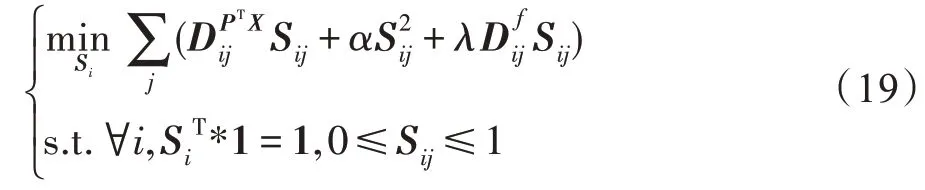
（更新）固定变量P、w、，则关于变量的优化函数可表示为：

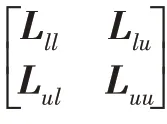
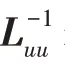
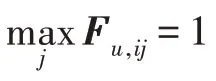
基于一致性约束的半监督多视图分类（SMCC）

输入：原始数据X=[,,…,x]∈R；维数；标签率；参数、、、。

输出：预测标签矩阵=[F;F]；投影矩阵=[,,…,P]。

2.迭代更新：

2.1 固定变量、w、，根据以下函数更新变量P：

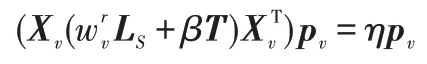
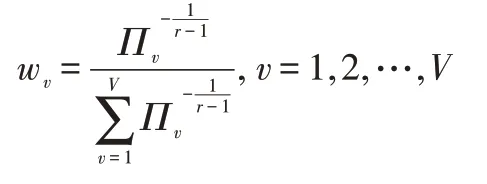
2.3 固定变量w、P、，更新变量：

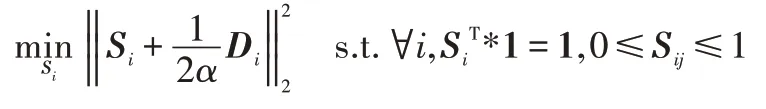
2.4 固定变量、w、P，更新变量：

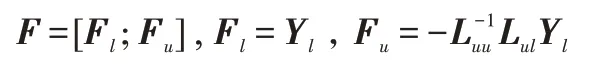
3.满足收敛条件。

3 实验与分析

本章对本文算法进行了详细分析，并在4 个基准数据集上与其他新颖的算法进行对比来验证SMCC算法的性能。

3.1 实验数据集与具体实施

本文算法分别在ORL、Yale、MSRCv1 以及Handwriting numerals 数据集上进行对比实验，其中各数据集的部分展示图如图2 所示。

图2 实验数据集部分展示图Fig.2 Sample images from experimental data sets

ORL 数据集是由40 个不同类别的400 张人脸图像组成。实验中，该数据集有包括4 096 维度的灰度特征、3 304 维度的LBP 特征以及6 750 维度的Gabor 特征的三种不同特征数据集被使用。Yale 数据集包括15 个类别的165 张灰度图像，其不同的特征集也分别由灰度特征、LBP 特征以及Gabor 特征组成。MSRCv1 数据集共有8 个类别的240 张图像。选取了树、建筑、飞机、奶牛、人脸、汽车以及自行车7类图像进行实验，其中每类图像含有30 张。四种类型的特征被提取：24 维的色矩（color moment，CM）特征、512 维的GIST 特征、254 维的CENTRIST 特征以及256 维的LBP 特征。HW（handwriting numerals）数据集由2 000 个0～9 的数字图像组成，每个数字有200 张图像。六种类型的特征被提取：76 维的FOU特征，216 维的FAC 特征，64 维的KAR 特征，240 维的PIX特征，47维的ZER特征以及6维的形态（morphological，MOR）特征。

在实验中，本文对比了标签传播（label propagation，LP）算法、AMGL 算法、MVAR 算法、MLAN 算法以及FISH-MML 算法。其中LP 算法是作为每个特征视图判别的基准。为了公平地对每个算法进行对比，从每类中随机选取了对应标签比例下的训练样本，其他样本用于测试。考虑到标签比例对应的标签数量可能为非整数，因此最后会对获取的标签数量进行向下取整。本文对所有算法都进行了10次实验并记录了分类准确率的平均值与标准差。其中最近邻的个数设置为9，的取值范围为[1.5，5.0]。值得注意的是，FISH-MML 算法最终的分类结果由NN 算法获得。

3.2 结果与讨论

通过大量实验得到了所有算法在4 个数据库上的不同标签比例下分类结果，如表2 与表3 所示，其中对表现最优的结果进行了加粗处理，n/a 表示为不适用。从数据结果可以得出，SMCC 算法在大部分情况下能够表现出最优的性能。

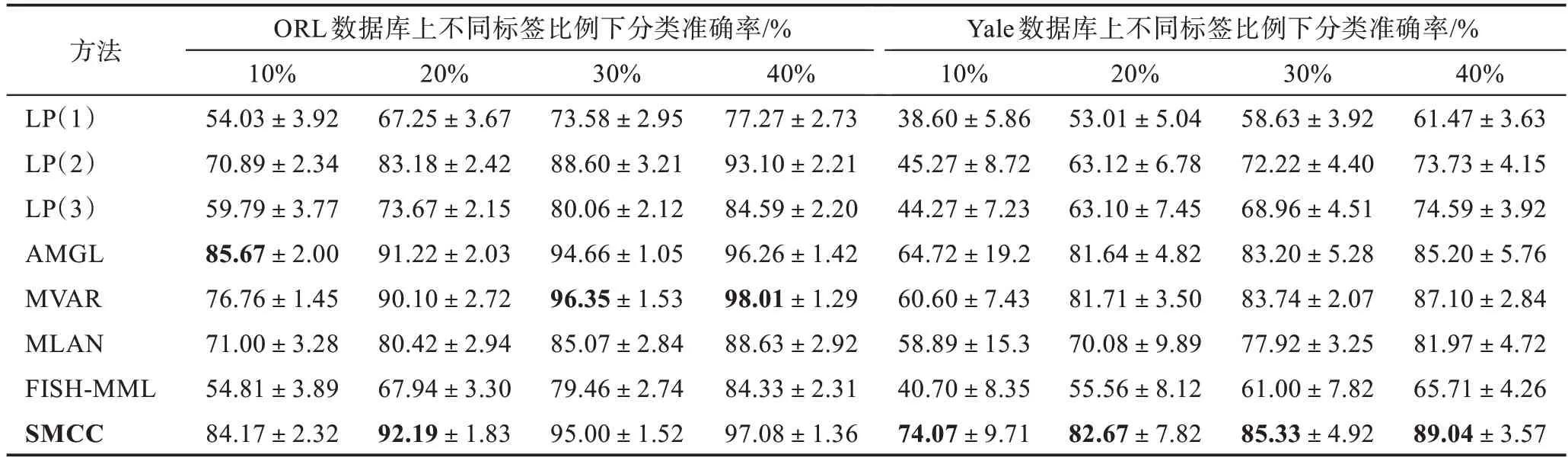
表2 不同算法在ORL 与Yale数据库中的性能（均值±标准差）Table 2 Performance(mean±standard deviation)of different algorithms on ORL and Yale databases

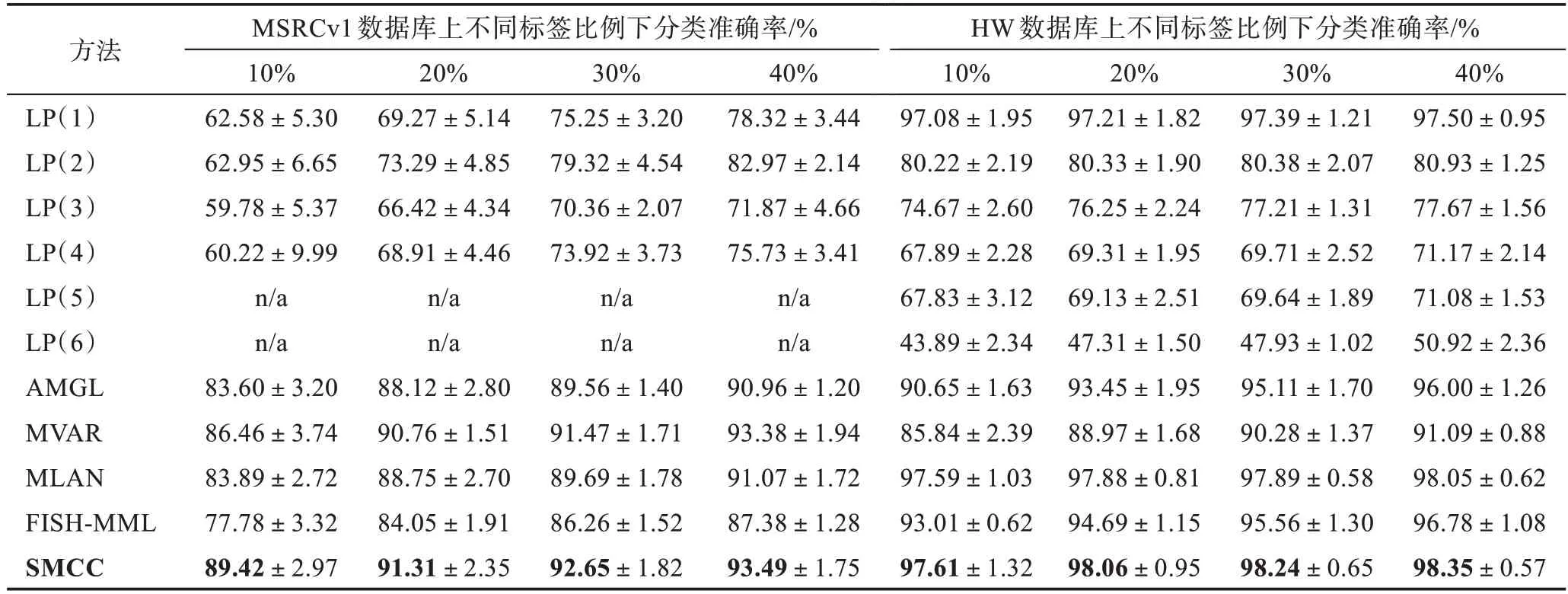
表3 不同算法在MSRCv1 与HW 数据库中的性能（均值±标准差）Table 3 Performance(mean±standard deviation)of different algorithms on MSRCv1 and HW databases

在ORL 数据集中，AMGL 算法在标签比例10%的情况下优于本文算法，其主要原因可能是在训练样本较少且不包含噪声或者阴影的情况下，对相似矩阵进行F 范数约束会损失部分判别信息，从而使得SMCC 算法性能略低于AMGL。MVAR 算法在标签比例为30%与40%的条件下表现优异，说明基于多元回归的自适应权重多视图算法在没有被污染的人脸数据中能够进行很好的拟合。在Yale 数据库中，本文算法在不同标签比例下都表现最优，特别在标签比例为10%的情况下SMCC 算法的准确率比AMGL算法高出了9.35 个百分点，其效果说明了基于一致性约束的半监督多视图分类算法在样本含有噪声以及阴影的情况下能够提取更多有效的判别特征用于分类。而基于一致性约束的FISH-MML 算法性能较低，主要原因是由于没有考虑到对每个特征视图进行合理的加权以及利用无标签样本中的结构信息。在MSRCv1 数据库中，对比次优的MVAR 算法，本文算法考虑了数据的局部结构以及每个特征视图的空间一致结构，从而提高了算法分类效果。在HW 数据库上整体算法的分类准确率都较高，其原因可能是FOU 特征中包含了足够多的判别样本有效信息。然而，MVAR 算法分类准确率较低，表明基于多元回归的算法对于一种类别用多种形式展示的数据判别性能较差。因此，通过对不同算法在不同数据库下获得的结果进行分析，本文算法考虑了数据的局部结构与不同视图之间的空间一致性结构，提取了原始数据有效的判别信息，并通过对相似矩阵进行F 范数约束以及自适应地为不同视图进行合理的加权，使得SMCC 算法在不同的数据库下都能获得较好的分类效果。

3.3 复杂度与收敛性分析

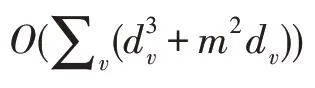
为了便于理解，所提出的算法（SMCC）在ORL、Yale、MSRCv1 与HW 数据库上标签比例为10%的条件下进行实验，得到的收敛性曲线如图3 所示。其中图3 中的（a）、（b）、（d）图显示，算法在数据库ORL、Yale 与HW 上迭代10 次后目标函数值趋于稳定状态。在图3（c）中可得到算法在MSRCv1数据库上迭代15次后收敛。因此本文算法是有效的且收敛速度较快。

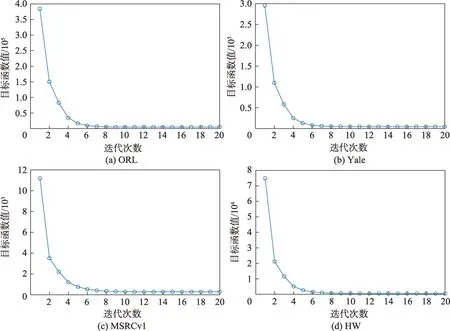
图3 在不同数据库上目标函数值与迭代次数的关系Fig.3 Relationship between value of objective function and the number of iterations on different databases

3.4 参数敏感度分析

为了分析正则化参数和对本文算法的影响，进行了大量的实验来评价在不同参数下SMCC算法的性能。不失一般性，本文在每个数据库标签比例为10%的条件下依次进行实验，首先分别设置两个参数（与）的取值范围为{10,10,10,10,10,10,10,10,10}，其更新的方法为更新一个参数时固定另一个参数。图4 展示了在4 个数据集上本文算法的分类精度与不同参数值的关系。

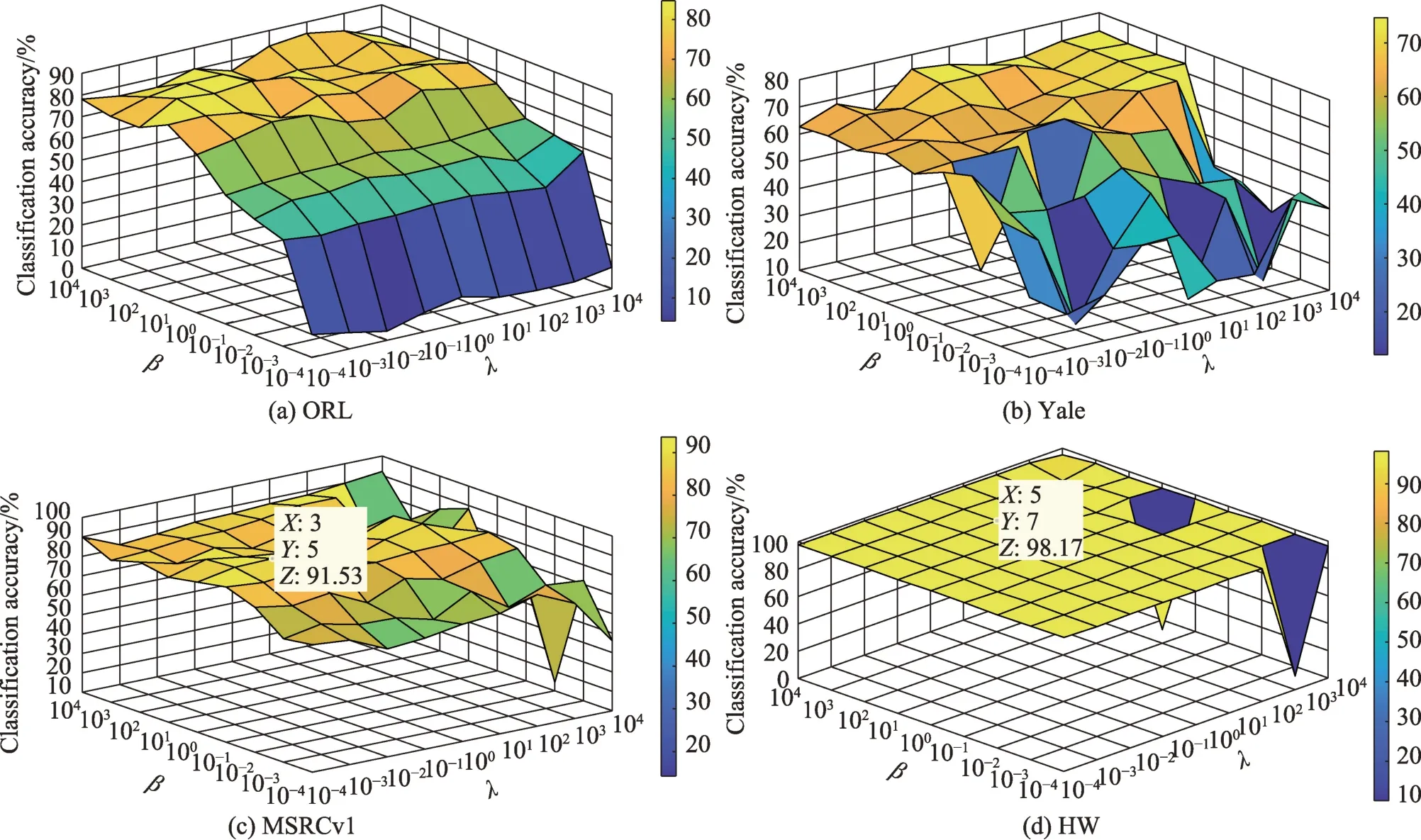
图4 不同数据库上参数β 和λ 对算法分类结果的影响Fig.4 Influence of parameters β and λ on algorithm classification on different databases

从图4 可观察到，当正则化参数和在选择合适的范围时，SMCC 算法能够达到满意的效果。特别对于HW 与MSRCv1 数据库，本文算法能够在参数广泛选择的范围内取得优异的性能。在ORL 数据库上，算法对参数的敏感度较低，且当>1 时能获得较好的效果。对于Yale 数据库，算法受参数的影响较大，仅当与属于[10,10]时性能相对较高。

4 结束语

本文通过结合多度量学习与自适应权重学习设计了一种新颖的半监督分类算法，即基于一致性约束的半监督多视图分类（SMCC）。具体而言，本文算法不仅考虑了多视图数据在希尔伯特空间中的不同视图之间存在着潜在的一致性结构，而且对在欧式空间中的数据进行了局部流形结构保留。更重要的是，对相似矩阵进行F 范数约束，有效提高了算法对噪音以及异常点的鲁棒性。此外，通过对每个包含不同特征信息的视图设置一个自适应的权重进行加权，提高算法的准确性，并基于LADM 方法对所提出的算法进行了有效的求解。在4 个基准数据库上的广泛实验结果表明，所提出的SMCC 算法整体上优于其他的半监督多视图分类算法。