面向多表数据连接投影和连接顺序的优化方法
2022-01-18宗枫博赵宇海王国仁季航旭
宗枫博,赵宇海+,王国仁,季航旭
1.东北大学 计算机科学与工程学院,沈阳110169
2.北京理工大学 计算机学院,北京100081
随着分布式技术的快速发展,人们对大数据的处理能力有了飞跃式的提高,众多优秀的大数据引擎也应运而生。大数据处理引擎有着许多与传统数据库相似的计算操作,同样也有许多近似的优化方法。同时大数据处理引擎也与传统数据库有很多质的区别,大数据处理引擎不再依赖于企业级服务器而是可以通过部署在成百上千台PC 上协同工作,网络对运行效率的影响相比传统数据库而言更加显著。
作为大数据处理引擎,当连接操作涉及到多个表时,连接排序对降低执行成本有相当大的效果。连接操作符通过两个表的公共属性将它们连接起来,优化器需要找到一个成本最低或几乎接近的执行计划。连接顺序的优化问题通常被认为是一个NP-Complete问题,执行计划的个数随着连接表的数量和数据源之间的连接关系数量增加而呈阶乘级增加,目前为止针对连接顺序的优化已经提出了许多方法,包括确定性算法、启发式算法、随机算法、混合算法等。但是与传统数据库不同的是,分布式大数据处理引擎的节点要远远多于传统分布式数据库,在MapReduce 框架下各节点间I/O 对网络传输造成的影响会随着中间数据量的增长而成倍放大,同时I/O 对执行效率的影响也被大幅放大。而在传统的连接优化算法中,通常只考虑连接顺序优化,通过减少全局的连接计算量来减少执行时间,而并不考虑同时优化每次连接的投影或通过减少全局的投影列数来减少I/O 代价,如图1 连接树中包括三个表、、,传统方法中的优化主要将表作为最小优化粒度考虑,比如通过表的行数直接估算比较⋈⋈和⋈⋈哪个为更优连接策略,但若将表细分为列来考虑,表下的[0,1]表示表包含两个不同属性的列,相同的数字表示列的属性相同。在保证最终连接结果不变的条件下,可将原连接树改变连接顺序为图2 所示连接树,中间表由(σ(⋈))变为(σ(⋈)),由于投影到中间连接表的列由变为了,减少了一列,则可能进而减少了I/O 代价。为了尽可能减少全局中间连接表体积进而降低I/O 代价,本研究设计了一个连接索引结构,结合动态规划算法在优化连接顺序的同时对每个连接表的投影关系进行优化,同时针对连接计算代价和I/O 代价进行了优化,有效地减少了多连接任务的运算时间和中间数据的传输量。

图1 原连接树Fig.1 Origin join tree

图2 改变连接顺序Fig.2 Modify join order
本文的主要贡献如下:
(1)设计了一种描述连接表中列关系的索引结构,此索引结构可以快速找到两个表的连接关系及每一列是否冗余列。
(2)基于此索引,结合动态规划算法在优化连接顺序的同时删除每次连接的冗余列,尽可能地减少所有中间连接表的体积。
(3)通过基于Flink 系统的实验对本优化系统进行了验证,实验结果显示本优化系统有效地减少了多连接任务的执行时间和中间数据的传输量。
1 相关工作
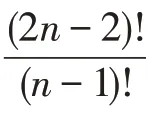
确定性算法通过完全遍历或在解空间中应用一些启发式剪枝方法,来执行解空间的确定性搜索,如IBM 的System R 中使用的动态规划算法,这个算法被几乎现有的所有商用RDBMS 系统使用,该算法通过动态剪枝解空间来进行完全遍历,通过迭代已有的连接关系并尽可能剪枝一些次优解来构造所有备选连接树,从而保证了动态规划算法在解空间中找到最优解。随机化算法通过预定义的变换规则在解空间内随机移动,不断寻找代价更低的点,当点不再移动的次数达到预定义的迭代次数阈值时,则认为当前的解为较优的解。如模拟退火算法(simulated annealing algorithm),它允许当前点向代价更高的点移动,从而降低了算法陷入局部最优解的概率,文献[6]中提出了一个算法参数来定义在给定时间点继续搜索的可能性,并和当前点与目标点的代价比例共同决定点移动的概率。
基因算法通过模拟生物的进化过程来寻找最优解,通过将一个初始群体(解集合)中的个体(解)随机交叉(crossover)和变异(mutation)产生下一代群体,将适应度最高(通过代价函数定义)的部分个体保留,并重复交叉和变异的过程产生下一代群体,当迭代次数达到预定义的阈值或者群体适应度已接近饱和,继续进化无法再显著提高适应度(通过阈值定义)时停止迭代过程。如PostgreSQL 中的Genetic Query Optimizer,它只考虑了左深树的情况,实现了精英选择算子(elitist selection operator),对于群体中的最优解,只进行交叉而不进行变异,防止群体中的最优个体在迭代到下一代时发生丢失,从而导致算法难以收敛到全局最优解。
混合算法混合了以上两种及以上的优化策略,比如巡回模拟退火算法(toured simulated annealing),该算法首先通过确定性算法确定几个初始点,然后对每个初始点进行模拟退火算法。
以上算法为主要基于传统关系数据库理论的多连接优化,优化的最小粒度为表,而在本文所提出的多表连接优化方法中优化的最小粒度为列。在传统数据库甚至一些节点数不高的分布式数据库中,连接表的列数,或者说连接表的体积对I/O 并不会造成显著影响,而连接表的行数,即连接表的元组数会对计算量产生很大影响,因此这些传统的多连接优化算法主要注重于对连接元组数进行优化以提高计算效率。随着MapReduce 框架在大数据处理中的广泛应用,一个任务的计算节点可能达到成百上千个,那么节点间I/O 带来的影响不再可以忽视。针对此问题,本文提出一种一般性的多表连接优化方法,可以在优化算法中同时考虑计算和I/O 的代价,并以动态规划算法为例,在动态规划算法的基础上同时实现对计算和I/O 的优化。并在实验中对多表多列数和多表低列数的情况进行了测试,证明了本文的优化方法不失一般性。
2 预备知识
对于批数据连接计算,Flink 系统在节点之间的传输有两种策略:RR(repartition-repartition)和BF(broadcast-forward)。而节点中的本地批数据连接策略和传输策略是完全独立的,在批数据传输完成后,每个连接实例将使用本地连接算法来连接分配的数据,本地连接策略包括两种:SM(sort-merge-join)和HH(hybrid-Hash-join)。
2.1 Flink 中的批数据传输策略
如图3 所示,RR 策略将两个批数据源R(等分为R1 和R2)和S(等分为S1 和S2)及它们的连接属性通过相同的分区函数发送到各个节点,每个节点被分配一个连接实例,确保有相同连接属性的批数据被发送到相同节点,RR 策略的代价即为将两个数据集通过网络进行完全shuffle。

图3 RR 传输策略Fig.3 RR ship strategy
如图4 所示,BF 策略中,批数据源S 保留在本地节点不通过网络传输,而每个节点的批数据源R 则被发送到其他所有节点,保证每个节点都能收到完整的批数据源R,因此BF 策略的代价仅取决于批数据源R 的大小和连接实例的数量,与批数据源S 的大小无关。显然当批数据源R 的大小远小于批数据源S时,系统更倾向于使用BF 策略。

图4 BF 传输策略Fig.4 BF ship strategy
2.2 Flink 中的批数据连接策略
如图5 所示,SM 的工作方式是本地节点的两个输入数据集按照连接属性分别进行排序(sort),然后将排序后的数据集进行合并(merge),最后对合并后的数据集进行连接。排序过程在内存中进行,当内存资源耗尽后则将内存中已排序完成的数据写入本地文件系统中,然后继续对传入的数据在内存中排序,全部数据传入完成后在本地文件系统中会存放每个输入流的若干不相交的有序子集,最后通过有序合并每个输入流的有序子集,同时对合并后的两个有序数据集进行连接。
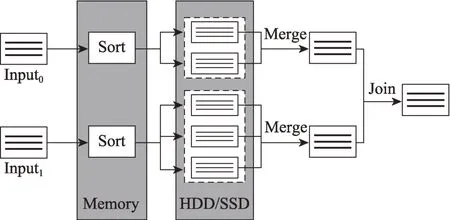
图5 SM 连接策略Fig.5 SM join strategy
如图6 所示,HH 方式将两个输入数据集分为build 端和probe 端,并且分为两个阶段工作:probe 阶段和build 阶段。在build 阶段中,将build 端的数据根据连接属性插入到哈希表中,若内存资源耗尽则写入到本地文件系统中。在probe 阶段中,probe 端数据根据哈希表索引与build 端数据连接,若索引到内存中的哈希表,则直接连接并输出,若索引到本地文件系统中的部分,则同样也将数据写入到本地文件系统中。在probe 端数据读完后,若本地文件系统中存在有溢出数据,则删除当前内存中的哈希表,通过存储的build 端溢出数据重新构建新的哈希表,并将本地文件系统中对应的probe 端溢出数据通过新的哈希表索引并连接,递归地进行此流程直到所有probe端数据都被处理完成。若内存资源能够容纳完整的哈希表,则HH 方式相当于普通的In-Memory Hash Join,有着极高的效率;即使在少量数据写入到本地文件系统的情况下,HH 仍然有着良好的性能。

图6 HH 连接策略Fig.6 HH join strategy
3 多表连接的投影和顺序优化
首先举例说明需要解决的问题,如图7 所示的一段连接关系的构建中,表与表连接生成中间表,key 为列1,这时需要确定哪些列需要通过投影关系保留到中,删除冗余列。

图7 列保留示例Fig.7 Example of column retention
对于列0,发现还有未连接的数据源包含此列,那么此列可能在后续连接中作为key,则此次投影中保留此列。
对于列1,在作为此次连接的key 后,发现此列不再存在于还未连接的任何数据源中,也不存在于最终结果result中,则可判定此列为冗余列,此次投影不再保留,列2 同理。
对于列3,发现原连接指定的result 中包含此列,则在每次投影中都需要保留此列。
通过解决以上所提到的冗余列问题,在同时考虑到连接顺序对连接效率的条件下,对原连接树图8使用本文提供的优化方法,优化后的连接树为图9,连接使用的数据集为TPC-H 标准测试数据集,其与Source表的对应关系如表1 所示。

图8 原连接树Fig.8 Origin join tree

图9 优化后的连接树Fig.9 Optimized join tree

表1 Source表对应的TPC-H 表Table 1 TPC-H table corresponding to Source table
为了执行此优化策略,本文设计了一种关于列和表的投影关系索引,通过此索引能够快速判断两个表的连接键值,以及连接后所需要保留的必要列。建立投影关系索引主要由两个模块组成:对列关系的溯源和列与连接关系索引的建立。
在得到投影关系索引后,可以基于此索引对每次连接的投影进行判断,及时删除冗余列减小I/O负担,具体实现方法为3.3节基于投影关系索引的投影判断。
为了衡量连接的优劣,需要设计一个综合考虑CPU 和I/O 的代价函数,基于前文2.1 节Flink 中的批数据传输策略可以得到I/O 的代价函数,基于前文2.2节Flink 中的批数据连接策略介绍可以得到CPU 的代价函数。通过将代价函数与动态规划算法结合可以得到连接顺序的优化结果,具体实现方法为3.4 节基于投影关系索引的连接顺序优化。
3.1 对列关系的溯源
此算法目的在于:对于连接树中指定一个表的一个列,能够找到以此列为key 具有连接关系的所有Source表的集合。
如算法1 所示,给定一个表和此表中的一个列,若表为Source 表,则创建一个记录节点(行3),记录此表的id 和列在此表中的位置(行4),将记录节点加入到中(行5);若表为Join 表,则对投影到列的输入表进行递归溯源,将记录节点加入到中(行9),若列同时为此Join 表的key,那么同样要对另外的输入表进行递归溯源,将记录节点加入到中(行11)。
Trace
输入:,the table currently accessed;,the column to be traced to the current access table.
输出:,the set of root tables found by traversing.
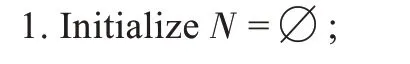

举例说明,与通过列6 为key 进行连接,需要得知哪些Source表包含了列6,这些Source表均有以列6 为key 的连接关系。
如图10 所示,对于中的列6 进行溯源,为Join表且列6为key,则列6的来源包括和,递归地对表溯源,找到和,则以列6 为key 具有连接关系的Source 表集合为{4,5,6}。

图10 对列6 的溯源结果Fig.10 Result of tracing column 6
3.2 建立投影关系的索引
此算法的目的在于,对于连接过程中的列,在每次连接的投影关系策略中,需要保留可能会在之后的连接中作为key 的列和包含在Result 中的列,为此建立一个十字链表形式的索引结构,由Source 表索引、Key 节点索引和连接信息节点构成,每个连接信息节点中记录所有能够作为同一连接key 的列,通过这个索引可以快速地确认当一次连接完成后哪些列在投影操作中可以被删除,减小对I/O 的影响。
这里说明用于建立所有key 列与Source 表的关系索引的算法2,对于所有Join 表的集合,遍历其中的每个Join 表,对的连接key 进行溯源得到记录节点集合(行3),创建一个新的连接信息节点记录这个集合(行4),遍历集合中的每个记录节点,通过Source 表索引查找,若存在已有的连接信息节点包含(行7),则说明所记录的key 和所记录的key 是等价的,因为这些key 所源自的Source 表互相存在连接关系,所以可以将与合并(行8),并用重新指向合并后的节点(行9);若不存在于对应Source 表的链表中,则说明这是一个有关于此Source 表的新的连接关系,将其加入到Source表的链表中(行12)。而若中的每个记录节点都不存在于已有连接信息节点中,则说明所代表key 不与已有的任何key 存在等价关系,则将其作为一个新的连接信息节点加入到key 节点索引中(行15)。
Key columns index
输入:,the set of JoinNode;,the linked list array of the relationship between the source table and the key information node.
输出:,the index array of key information node.

举例说明,在对表中的key 列3 进行溯源后,得到如图11 所示索引。左侧0~7 的纵表为Source表索引,对于一个节点,节点头(3)表示此key 列在整体连接树中的列编号为3,在所有的key 列中编号为2。指向节点内容1 表示此key 列在中的位置为1。指向节点内容0 表示此key 列在中的位置为0。

图11 对Join2 表中的列3 溯源得到索引Fig.11 Index of tracing column 3 in Join2 table
如图12 所示,在对表中的key 列6 进行溯源后,得到记录节点集合{列1,列1},通过Source 索引查询,发现并不与现存的连接信息节点有交集,那么作为新的连接记录节点{(6),列1,列1}加入到key 节点索引中。
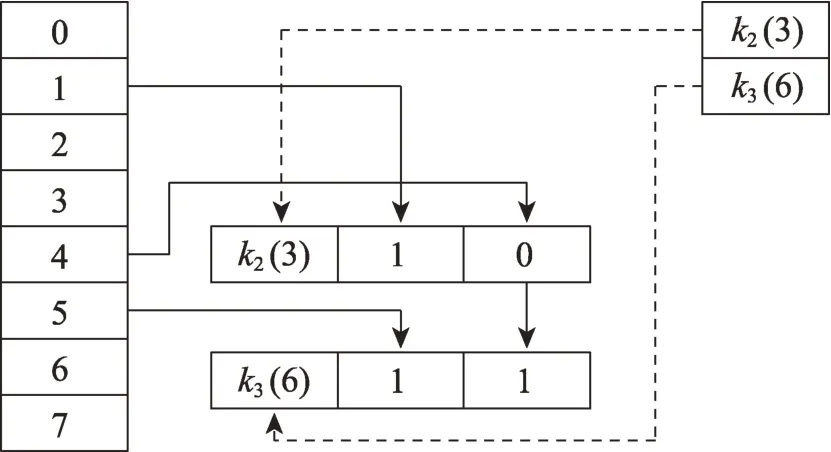
图12 对Join3 表中的列6 溯源得到索引Fig.12 Index of tracing column 6 in Join3 table
如图13 所示,在对表中的key 列6 进行溯源后,得到记录节点集合{列1,列1列0},通过Source 索引查询,发现与已有的节点存在交集,则将记录集合与节点合并。

图13 对Join4 表中的列6 溯源得到索引Fig.13 Index of tracing column 6 in Join4 table
通过此方法,最终得到如图14 所示连接树的索引结构。
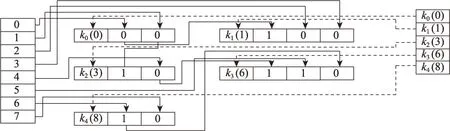
图14 原连接树的连接关系索引Fig.14 Join relations of origin join tree
同样,对于最终结果Result 表的所有列采取类似的算法得到关于投影到Result 表上所有列与Source表的关系索引。
3.3 基于投影关系索引的投影判断
此算法的目的在于,基于已有的投影关系索引,确定每次连接时需要保留的列。
如算法3 所示,对于两个输入表和,按照Source 索引,将中的所有已连接的Source 表所在的记录节点标记为finished(行7),将记录节点所在的KeyNode 节点标记为processed 表示已被遍历(行6);对进行同样的操作,若有KeyNode 被两次遍历,则说明此KeyNode 所代表的列同时存在于和中,即为和的连接key 列(行14~15)。若有Key-Node 中的所有列信息节点均被标记为finished,则说明此KeyNode 所代表的key 列连接Source 表已全部连接,那么此key 列在后续连接中不会再被使用(行12~13)。同时若此key 列不存在于Result 索引中,即与最终投影结果无关,那么在此次连接中不再对此列进行投影保留(行22)。基于此算法可以确保每次连接投影所保留的列只包括可能会在后续连接中所用到的key 列和最终结果的来源列。
NewJoinNode
输入:,InputNode0;,InputNode1;,linked list array of the relationship between the source table and the key information node;,index array of key information node;,index array of result information node.
输出:,the new JoinNode obtained by connectionand.


举例说明,如图15 所示,连接和表,通过Source 索引查询,发现和表同时包含列,则为和的连接key,连接结果为表,投影的key 列包括列。连接表和表,通过Source 索引查询表和表同时包含列,则为和的连接key,同时发现节点中的所有Source 表都已被连接,节点中的表还未连接,则此次连接投影的key 列包括列,不再投影保留列,并从索引中删除节点,删除后的索引如图16 所示。

图15 连接索引查询Fig.15 Query by join index

图16 删除冗余列及所在索引Fig.16 Delete redundant columns and indexes
3.4 基于投影关系索引的连接顺序优化
连接顺序的优化需要基于每次连接的代价计算,包括计算代价和I/O 代价。
对于输入,估算其表体积()为公式:

其中,()为的元组数,为经过投影关系索引判断后所保留的列。根据2.1 节中的传输策略介绍,可得RR和BF两种传输策略对应的传输代价公式:
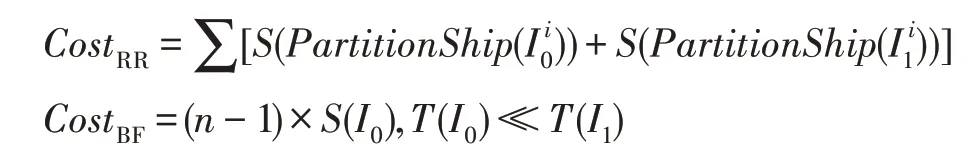

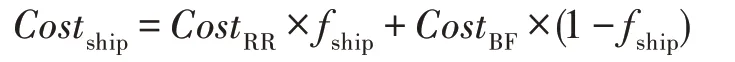
在假设和均匀分布的情况下,根据2.2 节中的连接策略介绍,可得关于Hybrid-Hash-Join 和Sort-Merge-Join 的CPU代价公式及I/O代价公式,其中为分配给Hash Table的内存大小。

据此可以得到CPU 代价公式和I/O 代价公式,其中为选择因子,1 表示选择Hash 策略,0 表示选择Sort-Merge策略。

据此得到每次连接的代价(⋈),其中、分别为节点间传输和节点与本地文件系统间传输的I/O 代价权重,为CPU 计算代价权重,三者均与系统硬件相关。

在假设输入表中连接属性的值在表中均匀分布的情况下,两表连接结果的元组数(⋈) 估算为公式:

其中,为连接键值,(,)表示在中不同值的数量。
通过代价公式和连接元组数计算,可以得到基于动态规划的连接顺序重排算法4。已知Source 表数量为,初始化状态矩阵,将每个Source 表依次加入到中(行4),对于矩阵中的每个节点,其行编号为(已连接的Source 表数-1),列编号为该连接树生成时起始的Source 表编号。对于D的连接树,需要连接的表数共为+1,且包含Source,那么可连接的备选项为之前已计算得出的局部最优连接树D,D(<,<)(行9~10),具体是否可连接,是否为重复连接,通过3.3 节等多个条件判断(行11)。通过此方法可以得到D节点的最优连接策略,这样从到D逐行完成状态转移矩阵,D中的最小代价的连接策略即为结果(行20)。此算法的最差时间复杂度为(),其中为连接表数。
Dynamic programming
输入:,number of source tables for all connections;,index of the source table.
输出:,optimal connection diagram.

4 实验分析
对于本文提出的投影和连接顺序优化方法,在Flink 系统上进行了实现,通过修改Plan 层的源码,对比优化后与优化前的执行时间及中间结果传输量。通过对比不同体积、不同数量、不同冗余度的连接树在优化前后的执行时间和中间数据传输量对优化方法进行了分析。
4.1 数据集和实验环境
本文采用的数据集为TPC-H 标准数据集,TPCH 是TPC 委员会发布的用于决策支持的测试标准。它由一套面向业务的即席查询和并发数据修改组成,其数据具有广泛的行业相关性,其中TPC-H 表的关系模式及表的内容如图17 所示。本文实验中所用到的不同规模的数据集均由TPC-H Tools 指定数据体积生成,其中体积分布如表2 所示。

图17 TPC-H 关系模式图Fig.17 Relational schema of TPC-H

表2 TPC-H 表数据体积及分布Table 2 Data size and distribution of TPC-H tables
在5 表到8 表的连接实验中,默认连接策略皆为优先连接体积较大的表,实验记录如无特殊声明并行度皆为36。
4.2 实验环境设置
本文所描述的相关技术细节,均在Flink 1.8.0 中进行实现,采用Java 语言进行编写。实验的运行环境及软硬件环境如下。
(1)硬件环境:实验采用的分布式环境由4 台服务器组成,1 台主节点,3 台从节点。从节点采用的服务器配置为:①CPU,Intel Xeon E5-2603 V4 *2,核心数目6 核心,主频1.7 GHz。②内存64 GB,主频2 400 MHz。③硬盘400 GB SSD。主节点配置为:①CPU,Intel Xeon E5-2603 V4 *2,核心数目6 核心,主频1.7 GHz。②内存128 GB,主频2 400 MHz。③硬盘400 GB SSD。
(2)软件环境:①操作系统Centos 7。②存储环境MySQL 5.6.45。③Flink 版本1.8.0,JDK 版本1.8.0。
4.3 实验结果分析
这里定义一个连接任务中的冗余列c和冗余率,c指此列在此后的连接中不再作为key,且不存在于结果列中,表示所有冗余列数量和占所有Join 表中的列数量的比例。
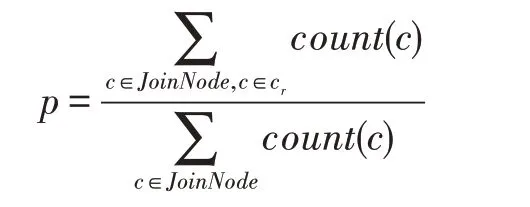
冗余率为0,即连接性能几乎只受连接顺序影响的情况,不指定数据传输策略和连接策略,由系统自动选择。
如图18 所示,连接顺序优化在表数较少的情况下优化效果并不明显,因为低表数下连接顺序的解空间同样非常小,最优解与默认解的执行效率也很少会出现较大差距。同时可以看出,5个table在700 MB规模以下的数据集执行时间几乎一致,可以判断系统启动执行的最小时间为14 s 左右,且5 个table 在700 MB 规模以下的数据集对系统资源消耗极小,没有显著优化效果。且通过优化前后几乎无差别的执行时间可以看出,5 个table 下的优化程序执行时间同样可以忽略不计,即使在小规模数据集计算上,优化程序仍不会对整体运算造成可见的负担。

图18 5 表连接的优化前后执行时间Fig.18 Execution time before and after optimization in 5 tables join
如图19 所示,在6 个table 下,大规模数据集对计算时间的影响已非常明显,并可以看出一定的优化效果。由于解空间仍然很小,且已加入的连接表之间的体积差距并不足够显著,虽然可以明显看到优化效果,但是优化前后的执行时间差距并不是很大。
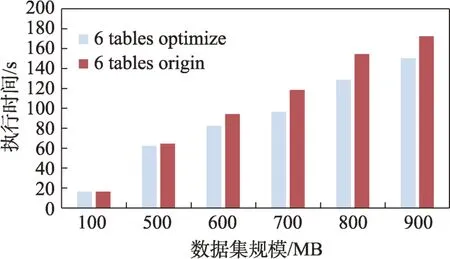
图19 6 表连接的优化前后执行时间Fig.19 Execution time before and after optimization in 6 tables join
通过图20、图21 可以看出,随着表数量的增加,优化效果变得非常显著。通过图22 可以看出,随着表数量的增加,优化效果变得更加明显,最大达到了58.69%。这是由于新加入的连接尾表体积非常小,大表与小表之间的体积差距非常小,连接顺序对连接效率的影响非常显著,且由于解空间的大小随着连接表的数量呈阶乘级增加,更容易找到效率远高于默认解的最优解。
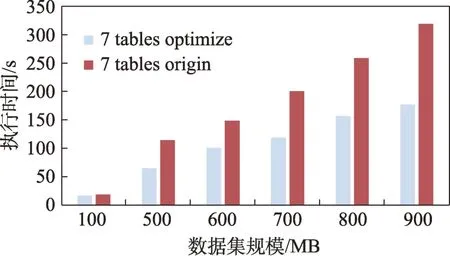
图20 7 表连接的优化前后执行时间Fig.20 Execution time before and after optimization in 7 tables join
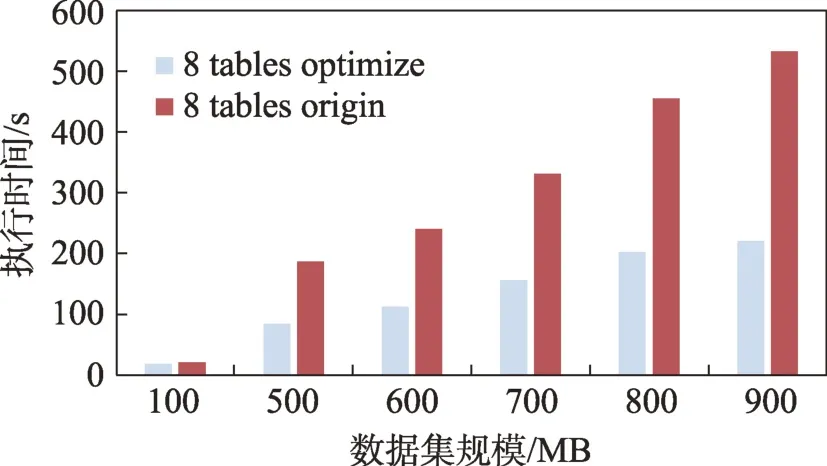
图21 8 表连接的优化前后执行时间Fig.21 Execution time before and after optimization in 8 tables join
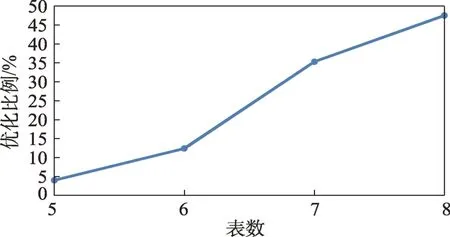
图22 不同表数下平均执行时间优化比例Fig.22 Average execution time optimization ratio of different tables
通过图23~图26 可以看到,优化程序对多表连接的中间数据传输有着固定的优化效果,由于各节点的数据传输量仅和连接树有关,不受系统基础运行时间影响,即使在低连接表数下也可以看到显著的优化效果。通过图27 可以看到,不同数据集体积下各表有着几乎一致的优化比例,6~8 个table 的连接优化比例在不同数据集下的差别均在1%左右浮动。由于本文采用的优化算法为确定性算法,对于同一连接树的优化策略是固定的,可以确定对于同一分布的数据集,在相同的优化策略下,中间数据传输优化比例与数据集体积无关。

图23 5 表连接优化前后的中间数据传输体积Fig.23 Intermediate data ship size before and after optimization in 5 tables join
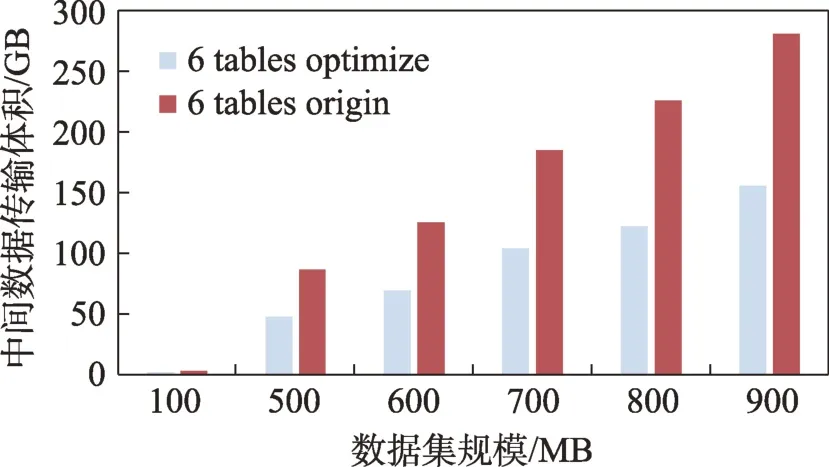
图24 6 表连接优化前后的中间数据传输体积Fig.24 Intermediate data ship size before and after optimization in 6 tables join

图25 7 表连接优化前后的中间数据传输体积Fig.25 Intermediate data ship size before and after optimization in 7 tables join

图26 8 表连接优化前后的中间数据传输体积Fig.26 Intermediate data ship size before and after optimization in 8 tables join
通过图27 与图28 对比可以得知,中间数据传输的优化比例远高于执行时间的优化比例,这是因为Flink 在执行时节点之间默认采用的为Pipeline 传输策略。这个策略规定了一个节点产生数据后立刻发送到下一个节点进行处理,Pipeline 策略一定程度上可以缓解由于大表在前产生的上游数据阻塞的情况。

图27 冗余率为0 时的中间数据传输体积优化比例Fig.27 Intermediate data ship size optimization ratio in redundant ratio 0

图28 冗余率为0 时的执行时间优化比例Fig.28 Execution time optimization ratio in redundant 0
这里选取8个table在不同冗余率(=0%,9.70%,19.40%,38.70%,51.60%)下的默认连接策略与优化后的连接策略进行对比,由于优化程序会清除连接中的冗余列,优化后的连接策略可视为冗余率为0。
通过图29 可以很明显地看到冗余率的不同对执行时间的影响。同样由于100 MB 体积数据处理时间的优化瓶颈不在于连接策略,优化比例和500 MB以上的数据存在较大差异。
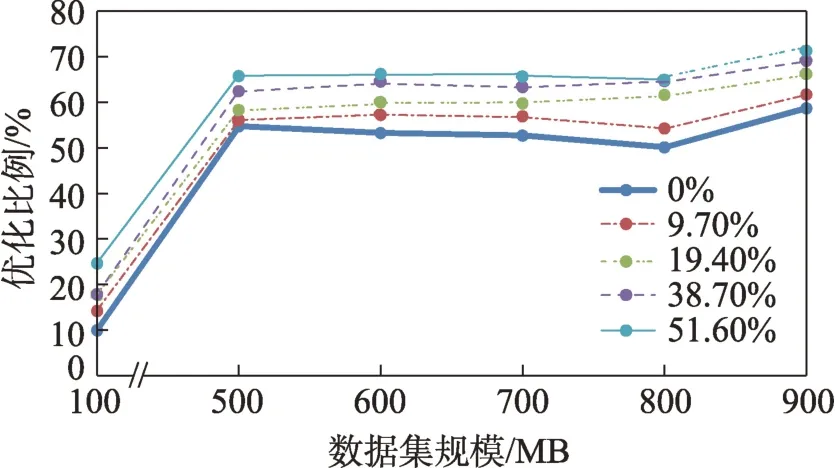
图29 不同冗余率下执行时间优化比例Fig.29 Execution time optimization ratio in different redundant ratios
由于冗余列的存在并不影响计算效率,不同冗余率对运算时间的影响仅来自于中间数据传输量对网络传输时间的影响,不同冗余率下执行时间优化比例明显和冗余率成正相关,但是彼此间差距并不巨大,冗余率从0%提升到51.60%,而时间优化比例仅提升了10%。
通过图30 可以看出,不同数据集体积下各表在同一冗余率下有着几乎一致的优化比例,这点与前文根据图27 所得到结论是相符的。在相同的优化策略和冗余率下,中间数据传输优化比例与数据集体积无关。

图30 不同冗余率下数据传输优化比例Fig.30 Data ship optimization ratio in different redundant ratios
同时可以看到冗余率对中间数据传输的影响要比执行时间的影响更大,冗余率从0%到51.60%,优化比例最大提升了19%。
表3 对比了0%和9.70%冗余率下500 MB 体积的8 个table 在默认连接策略下的中间节点的数据发送量。可以明显看到冗余列导致了不必要的数据传输,且冗余列若不及时通过投影清除会增加后续节点无用的数据发送量。
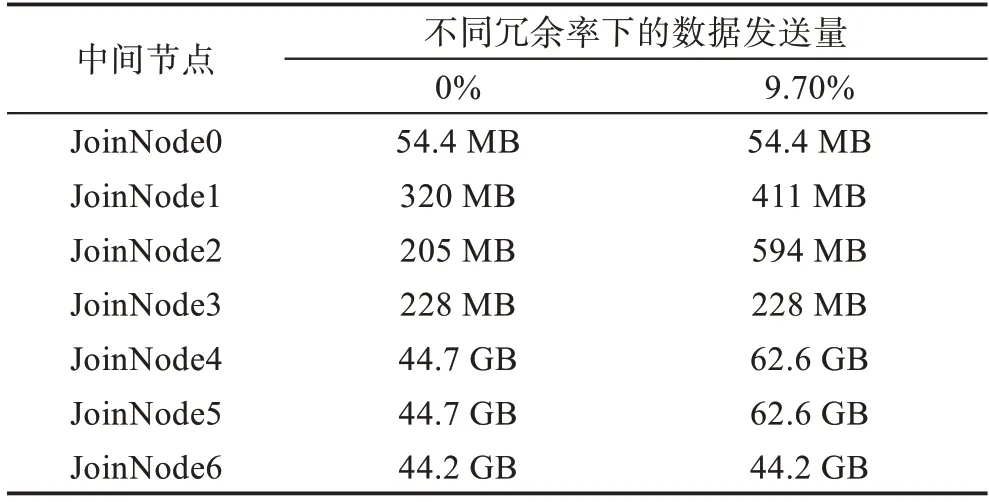
表3 0%和9.70%冗余率下中间节点的数据发送量Table 3 Data ship of intermediate nodes in 0%and 9.70%redundant ratios
图31 对比了不同并行度下的连接执行时间优化比例。同样在100 MB 规模的小体积数据上优化效果并不明显,随着数据体积的增大,在数据体积相同时,优化比例明显随着并行度增加而提高。

图31 不同并行度下执行时间优化比例Fig.31 Execution time optimization ratio in different parallelism
5 总结
本文针对大数据连接处理中投影关系的优化设计了一种基于投影关系索引的优化方法,并结合动态规划算法在Flink 中进行了实现。实验结果表明,本文方法所针对的冗余列问题确实对连接效率有着显著影响,随着冗余率的增加,连接效率会明显降低。本文所提供的优化方法在优化连接顺序的同时考虑到了冗余列的影响,可以大大减少连接任务的执行时间和中间数据传输量。
