考虑排放成本的共享电动汽车和共享停车位最优组合定价研究

姬杨蓓蓓 陈欣萌 成 枫

(上海大学 管理学院, 上海 200444)

0 引言

快速增长的机动车数量加剧了城市交通拥堵,且城市中心区域由于停车位不足造成的小汽车争抢停车位现象也进一步恶化了交通拥堵[1]。研究表明[2-4],城市中心区域,车辆由于寻找车位造成了停车巡位时间拉长,还导致环境污染加重、空气质量和生活舒适度的下降。尽管交通拥堵和交通污染等一系列问题突出,居民对于机动车驾驶的需求却持续增加,截至2018年9月,机动车驾驶人数达4.03亿,而同月全国汽车保有量仅3.22亿。驾照持证人数远远超出机动车的保有量,且缺口仍在进一步扩大。

针对以上背景,共享电动汽车便显示出巨大潜力。从私有小汽车出行模式转向为共享电动汽车出行模式对交通问题的缓解具有重要作用,也是非常值得探讨与创新的一种新模式。从社会层面,其作为一种节能减排的出行方式,具有减轻环境污染、降低能源消耗、减少机动车保有量、缓解交通拥堵等诸多优势[5-7];从个人层面,其作为一种替代私有小汽车的出行方式,比私人拥有小汽车大大增加了汽车的使用效率,弥补了自驾需求空隙、降低了个人出行成本、减轻买车和养车的经济压力。但是由于早高峰时段城市中心区域停车位的极度紧缺,限制了共享电动汽车在城市中心的出行需求。

在共享经济的大背景下,2017年3月发改委发布《关于开展城市停车场试点示范工作的通知》,首批5个城市开展城市停车场试点示范工作,以推动“互联网+停车”和车位共享新业态发展。我国在2019年9月发布的《交通强国建设纲要》中强调“优化交通能源结构,推进新能源的应用,倡导绿色低碳出行理念”[8]。因此本研究提出以“共享电动汽车+共享停车位”(Shared Electric Vehicle + Shared Parking,SEV+SP)相结合的方式,作为在早高峰时段私有小汽车和公共交通出行的一种补充方式,基于瓶颈经济学原理探讨如何组合设计共享电动汽车的时变租赁费用和共享停车位的停车费用,从而既能降低系统的交通排放,同时又能兼顾社会效益。

1 文献综述

以缓解交通拥堵,增加社会效益,降低污染排放等为目标,国内外学者更多聚焦于道路拥挤收费、公交车票定价以及停车费定价等方面。Chen[5]和Yang[9]构建了双目标优化模型,得出在考虑不同交通状况和交通排放时的道路拥挤收费与补贴定价标准。Li[10]等研究了在不确定性网络下的公交车最优定价模型,分析了市场制度分别为垄断市场、寡头竞争和社会最优时对最优公交票价结构的影响。肖玲[11]等基于瓶颈经济学理论,构建了私营停车场和公共停车场的NASH博弈定价模型,通过算例分析了私营停车场和公共停车场的停车收费对于社会效益的影响。

随着共享经济的发展,共享电动汽车具有使用率高、低碳、环保等特点,推广共享电动汽车被认为是减轻交通污染排放的一个解决措施[12-13]。关于共享电动汽车的定价研究,学者们主要针对如何增加共享租赁电动汽车公司收益、如何提高市场的稳定性以及如何促进共享电动汽车行业市场的发展等方面,还有一些学者讨论了共享电动汽车的定价策略将如何影响用户需求。针对增加公司收益,杨耀坤[14]构建了商业模式动态成本收益评估模型,研究了共享电动汽车租赁定价等关键因素对企业盈利性的影响。Jorge[15]等构建了混合整数非线性规划模型,进而确定了使共享电动汽车企业营利性最大的定价策略。针对提升市场稳定性、促进行业发展,黄毅祥[16-17]等通过构建联盟博弈模型,分析在共享电动汽车市场中构建价格联盟将如何影响各博弈主体的效益,分析了联盟模式下的价格形成机制、收益分配机制及联盟稳定性。针对价格策略对用户需求的影响,Xu[18]等通过构建混合整数凸规划模型,讨论了行程定价与车辆规模等关键影响因素如何影响用户需求,并确定了最优的行程定价。依托共享经济大背景,不仅共享停车行业持续发展,学术界也进行了一系列的研究,主要集中于提高共享泊位的利用率[19],开发共享泊位信息化管理平台[20-21],提高市场保有率[22]等。尽管关于共享电动汽车和共享停车位的研究已经比较丰富,但是针对共享停车位定价方面的研究较少,更鲜有以降低系统交通排放成本以及提高社会效益为双重目标的关于共享电动汽车时变租赁费用和共享停车费的组合定价研究。

本文的研究是基于瓶颈经济学方法展开的。瓶颈经济学在研究交通拥挤与交通分配方面具有显著意义,最主要的理论是Vickrey提出的瓶颈模型[23-24]。Vickrey假设早高峰时有固定数量的通勤者从家至工作单位,并且需要通过一条固定通行能力的瓶颈路段,所有通勤者的目标到达时间相同,且均衡时所有通勤者的个人出行成本相同,并且没有通勤者能够通过改变出行时间的方式降低个人成本[25]。此后,Arnott从道路收费与停车收费等领域对瓶颈理论进一步完善[26-27],Small[28]、Zhang[1,29]、Yang[30-31]和李乐园[32]等分别从参数设置、停车限制、车位预约以及瓶颈的可变通行能力等方面对瓶颈模型进行了深化。由于瓶颈经济学模型成功地应用于出行成本、停车管理、道路收费等方面,并且可以直接推导出相关参数的解析解,以描述关键参数之间的关系,因此在交通管理与定价优化方面应用广泛。本研究将瓶颈经济学理论引入到共享电动汽车与共享停车位的最优组合定价研究中,定量的分析结论可为管理者制定决策提供参考。

2 “共享电动汽车+共享停车位”(SEV+SP)的可行性分析

通常居住区停车需求的时空特点与周边办公建筑物具有互补特征,居住区的业主车辆呈“朝出夕归”的出行特征,从而居住区白天工作时段停车位明显剩余,具有优良的对外共享条件。我国的城市规划中,居住区一般都毗邻商业、办公等业态的建筑物,在共享车位停车后步行距离适中,符合共享停车的基本条件。

此外城市中心区较早建设的商业、办公建筑物配建的停车位指标较低,远远不能满足现阶段私有小汽车的停车需求。同时城市中心区域由于土地资源有限和交通拥堵不断加剧,管理部门不鼓励建设更多的私有小汽车停车位来缓解商业和办公建筑物的停车需求。这就造成私有小汽车在早高峰时段由于争抢有限的停车位产生内耗,大大增加了道路拥堵并增加了尾气排放[1]。在共享经济的背景下,利用毗邻居住区白天空闲的停车位,提供给前往城市中心的办公或商业建筑物的出行者另一种出行选择,即“共享电动汽车+共享停车位”(Shared Electric Vehicles + Shared Parking, SEV+SP)的出行模式,可以有效地缓解上述早高峰出行矛盾。

通常,政府和管理部门对公共交通票价、停车场收费以及共享电动汽车的时变租赁费制定政府指导价,相关企业不得超过政府核定的最高收费标准。而政府为了实现决策目标,可以对共享停车场予以限价,如限制最高价或最低价,也可以对共享电动汽车的租赁公司予以补贴或进行价格指导。根据政府对社会效益和交通排放的重视程度,通过对不同管理目标加权来反映目标的优先级。因此,本研究以政府和交通管理部门为决策主体时,对共享停车费用和时变租赁费用进行组合优化具有可行性。

本文将基于瓶颈经济学在早高峰的城市中心区域,探讨以“共享电动汽车+共享停车位”(SEV+SP)为补充的出行方式是会加剧交通拥堵还是会缓解交通拥堵?如何采取价格调节的方式,通过优化“共享电动汽车+共享停车位”(SEV+SP)的数量,可以既减少城市交通排放又可以增加社会效益?本文将建立带权重的最大化社会效益和最小化系统交通排放成本的双目标优化模型,约束条件为多模式出行网络的用户均衡,求解共享电动汽车的时变租赁费用和共享停车费用的最优组合定价。

3 问题的描述

本文对两种出行模式进行对比分析,即双模式(Dualmode)出行方式和多模式(Multi-mode)出行方式。

双模式(Dual-mode)出行方式:路网中仅包括私有小汽车和公共交通两种出行方式,经典的双模式瓶颈模型是在单OD的交通网络的早高峰出行路网中,即一个出发地(居住区域)一个目的地(工作区域)组成的交通网络[11],并满足以下条件:①私有小汽车直接停放在办公建筑物的私有停车场,因此步行时间可以忽略;②城市中心区域办公建筑物的私有停车场远远不能满足私有小汽车的出行需求,因此办公建筑物的私有停车位数量小于私有小汽车出行的需求;③假设公共汽车通勤时间固定,虽然公共汽车出行时间较长,但是乘坐公共汽车的用户都可以准时到达。

多模式(Multi-mode)出行方式:在双模式出行方式中引入SEV+SP的出行模式作为通勤方式的补充就形成了多模式通勤,即:私有小汽车、SEV+SP、公共交通这三种出行方式,如图1所示,并具有以下特点:①私有小汽车和SEV+SP出行者使用同一个有瓶颈的普通道路;②私有小汽车可以直接停放在办公建筑物的私有停车场(同上述双模式),无步行距离。但是考虑共享电动汽车停放在毗邻共享停车位后需要步行至办公建筑物,如图1中加粗实线所示,假设SEV+SP用户需步行相等的时间T到达办公建筑物;③根据实际情况,毗邻居住区有条件为共享电动汽车提供充足的共享停车位;④由于毗邻居住区的共享停车位需要在大多数业主早晨上班后才可以用来共享,因此SEV+SP用户均会选择较晚出发;⑤假设乘坐公共汽车的用户都可以准时到达。

图1 多模式(Multi-mode)下通勤者出行交通走廊Figure 1A simplified transportation network in multi-mode

4 双模式(Dual-mode)用户均衡下系统交通排放成本与社会效益

根据瓶颈经济学基本原理,在用户均衡(UE, User Equilibrium)原则下每一个用户的出行成本均相等。在双模式下,私有小汽车用户的出行成本和公交车用户的出行成本相等,此时形成了双模式的用户均衡。

4.1 双模式(Dual-mode)系统用户均衡求解

假设路网中每天有N个早高峰通勤者,所有通勤者的目标到达时间相同为t∗,瓶颈处的通行能力为s。选择私有小汽车通勤的用户数量为Np(假设每辆私有小汽车仅有1位驾驶员驾驶),选择公交车出行的通勤用户数量为Nb,考虑到实际情况,办公建筑物的私有停车位数量为n0。 本文首先求解双模式的用户均衡,计算排放成本,同时给出双模式下的社会效益与系统交通排放成本。

4.1.1 双模式下私有小汽车和公交车出行成本的定义

由于办公建筑物的停车位有限,私有小汽车的出行量即为办公建筑物的停车位数量:Np=n0。由ADL模型[33],私有小汽车个人出行成本Cp包括三部分:出行时间成本、非准点到达的惩罚成本和支付的停车费用,可由公式(1)表示。

其中,T(t)是时刻t出发的私有小汽车的总通行时间,包括自由流通勤时间和排队时间,即T(t)=T0+Tq(t)[25,34], 自由流下的出行时间为T0,时刻t出发的私有小汽车的排队通行时间是Tq(t)。m是私有小汽车通勤者支付的停车费。假定每单位通行时间的等价货币费用为α元/小时,每单位早到时间的等价货币费用为β元/小时,每单位迟到时间的等价货币费用为γ元/小时,由Small的研究[28],假设γ＞α＞β＞0 。

对于路网中的公交车出行者,考虑到拥挤因素,使用公共交通通勤的人数越多用户感受的拥挤越高。其个人出行成本Cb包括三部分:支付的公交车票面费用、出行时间成本和拥挤成本,如公式(2)所示。

这里,b是公交车的票价,Tb是公交车的通勤时间,k为车内拥挤系数(k＞0),Nb是公交车通勤的人数。可以看出,公交车的个人出行成本与公交车的通勤人数成正比例关系。

4.1.2 双模式下私有小汽车和公交车排放系数

假定私有小汽车行驶包括两个部分:自由流下的匀速行驶和在瓶颈处怠速行驶[35-36]。本文将私有小汽车的排放定义为自由流时间排放和排队时间排放,定义排放系数用于描述汽车排放对于环境的负面影响。用表示私有小汽车自由流单位时间排放成本,表示私有小汽车排队的单位时间排放成本。根据相关研究,汽车在拥堵过程中加速度的绝对值大于0,因此私有小汽车在自由流的单位排放成本小于排队单位时间排放成本

由于设置了公交车线路,因此公交车在行驶中无需排队,公交车行程时间即为公交车的自由流通行时间Tb。定义λb为公交车在行驶过程中单位时间的排放成本,结合实际情况,在整个行程过程中,私有小汽车的自由流单位排放成本小于公交车的单位排放成本[35]。

4.1.3 双模式的用户均衡

根据瓶颈经济学基本原理,当整个网络处于均衡状态时,每一位用户的出行成本是相等的,即没有一个用户可以通过改变出行时间来降低自身出行成本[25]。当私有小汽车和公共汽车都有通勤者选择时,用户均衡状态的表达式如公式(3)所示。

由于私有小汽车停车受限,即终点处的停车位数量不能满足所有的私有小汽车潜在出行量。此时,私有小汽车出行者会通过提前出发时间争夺停车泊位[1]。

4.2 双模式(Dual-mode)的系统交通排放成本(TECdual,Total Emission Cost)与社会效益(TRdual, Total Revenue)

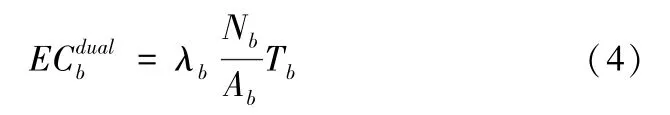
其中,Ab是早高峰每辆公交车的平均承载人数,取决于公交车的荷载量与早高峰通勤人数。

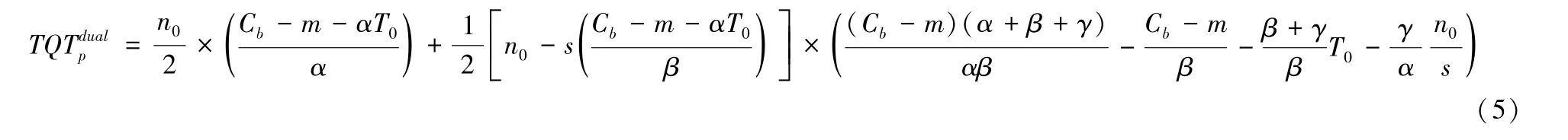
私有小汽车排放成本ECdualp的具体表达形式如公式(6)所示:

因此,在停车受限的双模式均衡下的系统交通排放成本(TECdual, Total Emission Cost)包括私有小汽车交通排放成本和公交车交通排放成本:

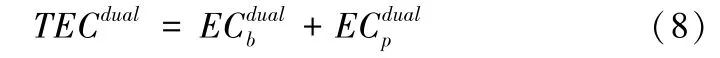
定义社会效益包括:私有小汽车停车场的总收益和公共交通的总票价收入。因此双模式下的社会效益(TRdual, Total Revenue)表达式为:

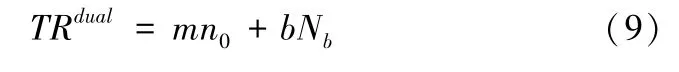
5 多模式(Multi-mode)用户均衡下系统交通排放成本与社会效益

多模式的用户均衡是选择私有小汽车出行、选择“共享电动汽车+共享停车位”(SEV+SP)出行和选择公共汽车出行的个人出行成本均相等。

5.1 停车受限下的多模式(Multi-mode)用户均衡求解

假设每天有N个早高峰通勤者,所有通勤者的目标到达时间相同为t∗,瓶颈处的通行能力为s。选择私有小汽车通勤的用户数量为Np(假设每辆私有小汽车仅有1位驾驶员驾驶),终点处办公建筑物的私有停车位数量为n0且不能满足私有小汽车出行需求,选择公交车出行的通勤用户数量为Nb。此外,还有Ns个早高峰通勤者选择SEV+SP出行模式(假设每辆共享电动汽车仅有1位驾驶员驾驶)。下面列出多模式下的用户均衡方程,并计算排放成本,同时给出多模式网络中停车位受限情况下的社会效益与系统交通排放成本。

5.1 .1多模式下共享电动汽车出行成本定义

多模式下私有小汽车、公交车用户出行成本与双模式相同,见公式(1)和(2)。选择SEV+SP模式的用户个人出行成本由五部分组成:出行时间成本、非准点到达的惩罚成本、共享电动汽车使用时变租赁费用、步行时间成本、共享停车费用。因此,共享电动汽车用户个人出行成本Csev如公式(10)示:

其中,η是共享电动汽车的单位时变租赁费用,λ是每单位步行时间的等价货币费用,T为毗邻居住区共享停车场距离工作目的地的步行时间,τ为共享停车费用,其他参数同公式(1)。

5.1.2 多模式下私有小汽车和共享电动汽车排放系数

多模式下私有小汽车和公交车的单位排放成本与双模式下的单位排放成本相同。

共享电动汽车的行驶包括两个部分:自由流下的匀速行驶和在瓶颈处怠速行驶。本文将电动汽车的排放定义为自由流时间排放和排队时间排放,用表示共享电动汽车自由流单位时间排放成本表示共享电动汽车排队单位时间排放成本,且

由于共享电动汽车排放相对私有小汽车排放少[37],假定共享电动汽车的自由流单位排放成本和排队单位排放成本都小于私有小汽车,即且共享电动汽车的自由流单位排放成本小于公交车的单位排放成本,也就是

5.1.3 多模式用户均衡求解

根据瓶颈经济学基本原理,当整个网络处于均衡状态时,每一位用户的出行成本是相等的,当私有小汽车、“共享电动汽车+共享停车位”、公共汽车都有通勤者选择时,均衡状态的表达式如公式(11)所示。

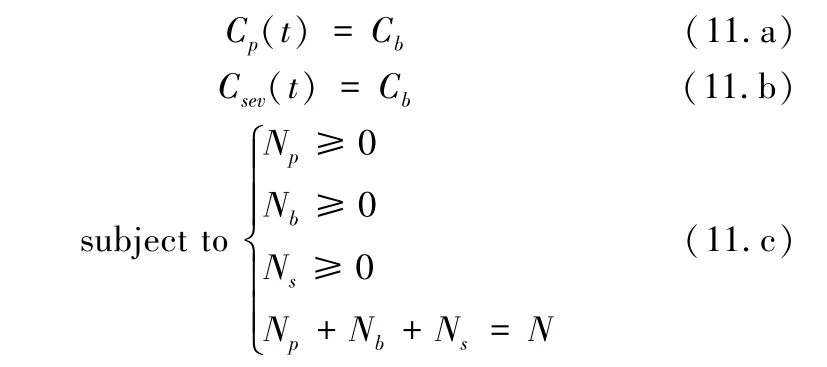
参考肖玲[11]、Liu[38]等对瓶颈模型解析解的表达方式,多模式均衡时,私有小汽车通勤者和SEV+SP通勤者具体出行时间的解析表达式如表1所示。图2给出了瓶颈处私有小汽车通勤者和SEV+SP通勤者的累积到达情况,私有小汽车通勤者会提前出发来争夺有限的停车泊位,根据前述假设,私有小汽车在t1~t5时间段内出发,并在t3~t9时段到达办公建筑物停车场。SEV+SP通勤者需要在毗邻居住区的业主大部分离开后才可获得共享停车位,因此SEV+SP通勤者均后出发,出发时段为t7~t11,到达共享停车位的时段为t9~t12,步行至办公建筑物的时间为t10~t13。

表1 用户均衡时多模式下通勤者具体出行时间Table 1Specific travel time of commuters in multi-mode user equilibrium

图2 瓶颈处私有小汽车通勤者和SEV+SP通勤者的累积到达情况Figure 2Cumulative arrivals of private vehicles and SEV+SP on the bottleneck

如图2所示,折线段ABC表示私有小汽车用户出发时间,折线段FED表示私有小汽车用户到达瓶颈时间,直线段FGH表示私有小汽车用户到达办公建筑物时间;直线段IJ表示SEV+SP用户出发时间,直线段LK表示SEV+SP用户到达瓶颈时间,直线段HK表示SEV+SP用户到达停车场时间,直线段MN表示SEV+SP用户到达办公建筑时间。

5.2 多模式(Multi-mode)的系统交通排放成本(TEC, Total Emission Cost)与社会效益(TR, Total Revenue)

路网中私有小汽车排放成本包括私有小汽车自由流通勤时的排放和排队时的排放,私有小汽车总自由流时间为图2中的ABCDEF区域,总排队时间为DEFGH区域,私有小汽车交通排放成本的具体表达形式如(13)所示:

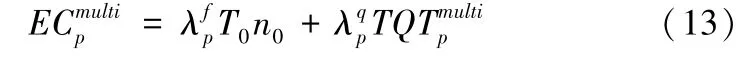
路网中共享电动汽车排放成本包括自由流通勤时的排放和排队时间的排放,共享电动汽车总自由流时间为区域IJKL,总排队时间为区域HKL,共享电动汽车交通排放成本的具体表达形式如公式(15)所示:

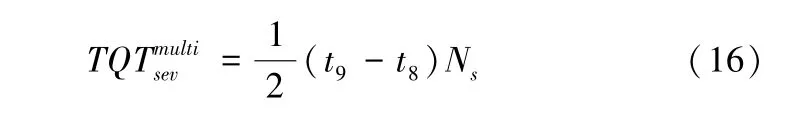
多模式下系统的总排队时间TQT为私有小汽车排队时间与共享电动汽车排队时间之和,因此:

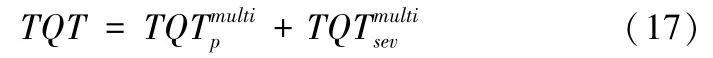
由此可得,平均排队时间AQT:

因此,在停车受限的多模式用户均衡下的系统交通排放成本TEC包括公交车排放成本、私有小汽车排放成本和共享电动汽车排放成本,具体表达式为:

多模式下的社会效益在双模式的基础上,增加了共享电动汽车公司盈利[39](TSP, Total Shared Profit)。因此多模式下的社会效益包括三部分:私有小汽车停车场的总收益和公共交通的总票价收入以及共享电动汽车公司的盈利。其中共享电动汽车公司的盈利又包括了行程过程中时变租赁费用的收益和共享电动汽车的停车费收益,共享电动汽车公司盈利具体形式为:

因此多模式下的社会效益(TR, Total Revenue)表达式为:

6 多模式下SEV+SP的最优组合定价

在多模式交通路网中,通过组合优化共享电动汽车时变租赁费用η和共享停车费用τ,从而达到最大化社会效益TR和最小化系统交通排放TEC的目的。本研究构建了如下的双目标优化模型,决策主体为政府和交通管理部门,约束条件为共享电动汽车和共享停车位定价变化下的用户均衡。模型如公式(22)所示:

当管理者同时追求两个目标的最优化时,可以通过评价函数法,将双目标优化模型转化为一个评价函数[40]。在这里选择线性加权的方式予以转化,权重表示管理者对于目标的重视程度。由于目标函数包括总的社会效益与系统交通排放成本,令w为社会效益的权重,1-w为系统交通排放成本的权重。因此将双目标优化模型转化为函数F(η,τ)。

假设最优的组合定价是(η∗,τ∗),F(η∗,τ∗)≥F(η,τ),在双模式均衡的基础上,求解得到能够使多模式用户均衡时η和τ的组合,并且得到使得目标最优的算法的具体描述如下。

第一步:a∈[0,maxη],b∈[0,maxτ]设定数组a、b与F(η,τ)分别表示时变租赁费用、共享停车费用与目标函数值。给出一个足够小的正数ε作为固定步长与收敛准则。设定i为总的迭代次数,令i=0,a(0)=0,b(0)=0,ε=0.001。

第二步:对于给定的a(i),b(i)可以得到共享电动汽车用户的个人出行成本Csev和公共汽车用户的个人成本Cb,如果,则进行第三步;如果不成立,需要考虑共享电动汽车用户的数量Ns,当Ns≤N-n0时,i=i+1继续进行第二步;当Ns＞N-n0时,退出循环。至此可求得使系统均衡的所有(η,τ)组合。

第三步:对目标函数值F(η,τ)进行排序,并得到最大目标函数值F(η∗,τ∗)与最优的费用组合(η∗,τ∗)。

7 算例

假设通勤者从家出发到公司上班,需要通过一条通行能力有限的瓶颈道路。设置参数α=1元/小时,β=0.9元/小时,γ=1.01元/小时(γ＞α＞β[23,28,35]),λ=0.3元/小时,自由流时间T0=0.5小时,出行总人数N=4900人,瓶颈通行能力s=70辆/小时,目标到达时刻t∗=8:00。私有小汽车在办公建筑物内的停车费用m=5元/次,办公建筑物内的私有小汽车停车位数量为n0=160辆,忽略办公建筑物私有停车场到工作目的地的步行距离;通常停车后人们可接受的步行距离最长为500米[41],可接受的步行时间约12分钟[42],假设毗邻居住区的共享停车场与办公建筑物的步行时长T=0.15小时。考虑到实际情况,共享电动汽车仅作为出行方式的补充,其数量不能无限增大,假设共享电动汽车的数量小于等于私有小汽车数量。设定共享电动汽车时变租赁费用和共享停车费用在合理范围内变化η∈[0,8]元/小时,τ∈[0,6]元/次。

对于公交线路,一辆公交车的早高峰平均载客量Ab=60人。假设公交通行时间Tb=1小时,公交出行的拥挤系数k=0.001,公交乘坐费用b=2元/次。因此公交车用户的个人出行成本为:

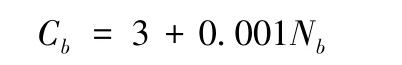
假设私有小汽车自由流每车每单位时间的排放成本=3元/(车·小时);排队时每车每单位时间的排放成本=10元/(车·小时);公交车每车每单位时间的排放成本λb=75元/(车·小时)[35];由于共享电动汽车具有排放较低的特点,假设共享电动汽车自由流每车每单位时间的排放成本=1元/(车·小时);共享电动汽车排队时每车每单位时间的排放成本=3元/(车·小时)[37]。

为了说明组合定价变化对系统产生的影响,下文首先介绍时变租赁费用η与共享停车费用τ变化时系统的变动情况。最后求解权重不同时分别使得目标函数最优的最优组合定价。

7.1 共享电动汽车时变租赁费用η与共享停车费τ变化对系统的影响

本研究将讨论共享电动汽车时变租赁费用η和共享停车费τ的组合定价,在多模式出行网络均衡时,对系统交通排放成本TEC、选择SEV+SP出行的用户数量Ns、交通拥堵状况AQT以及社会效益TR的影响关系。

7.1.1 共享电动汽车时变租赁费用与共享停车费对系统交通排放成本的影响

图3为共享停车费τ和时变租赁费用η变动时系统交通排放成本TEC及共享电动汽车用户数量Ns的变化关系图。在共享停车费用τ一定时,随着共享电动汽车时变租赁费用η的减少,Ns逐渐增大,即由于费用较低,更多出行者愿意选择SEV+SP出行模式。而时变租赁费用η和共享停车费用τ较高时,Ns趋于0,即说明过高的定价使得没有出行者愿意选择SEV+SP出行模式。

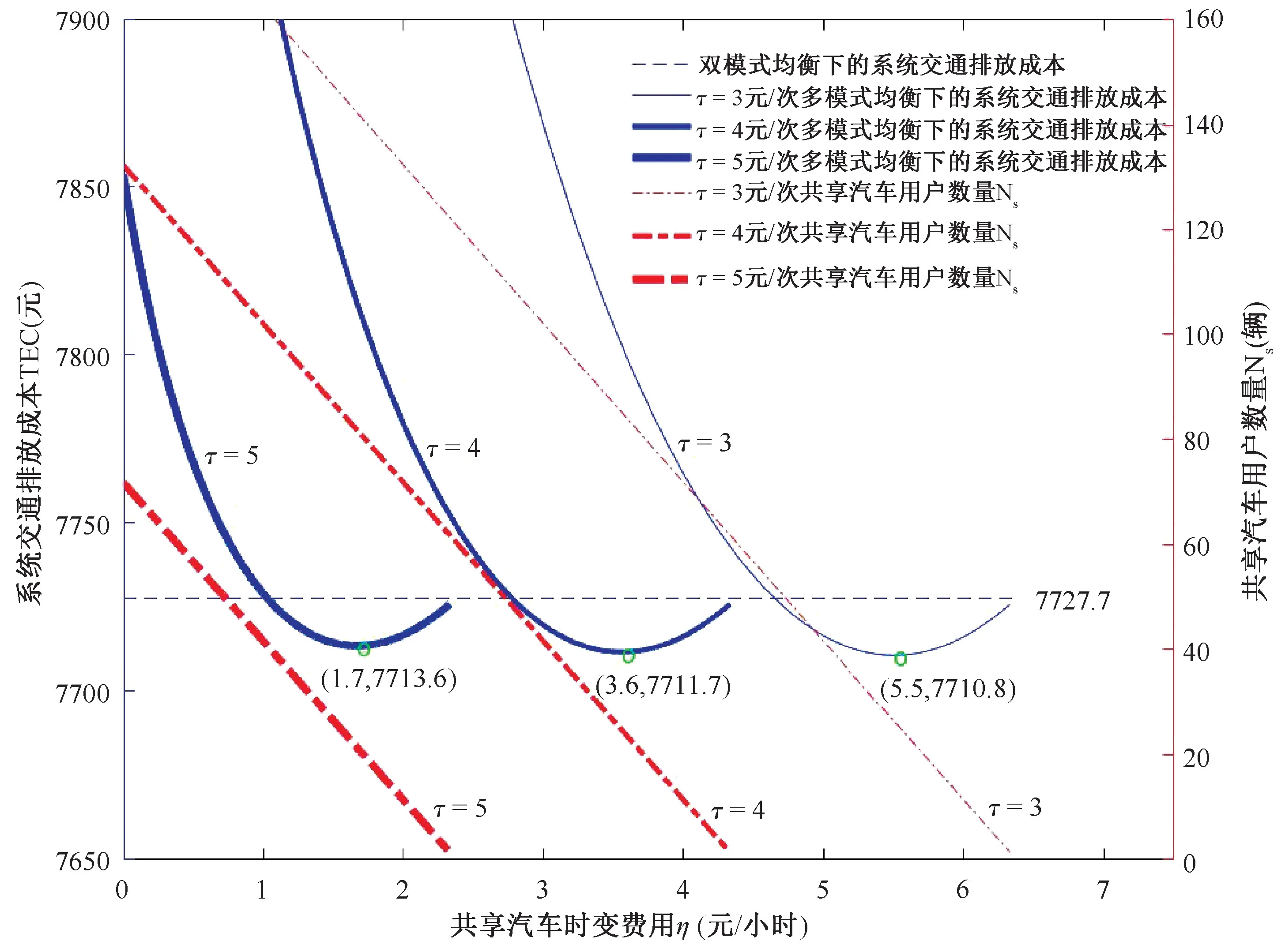
图3 共享停车费用和时变租赁费用对系统交通排放成本(左侧纵坐标)及共享电动汽车数量(右侧纵坐标)的影响Figure 3Total emission cost (left ordinate) and the number of shared electric vehicles (right ordinate) under different levels of the shared parking fee and time-dependent fee

多模式下系统交通排放成本TEC随着时变租赁费用η的增加先减少后增加,如图中实线所示。时变租赁费用η较低时,SEV+SP用户数量较多,引入SEV+SP的多模式出行方式相比于双模式反而增加了系统交通排放成本,也就是说在城市中心区域过多地鼓励共享电动汽车出行对交通排放非常不利。由图3可见,应该将共享电动汽车的时变租赁费用和共享停车位停车费用设计在合理范围之内,才能达到有效减少系统交通排放成本的目的。例如,多模式均衡时,当共享停车费用τ为5元/次,在时变租赁费用η为1.7元/小时,系统交通排放成本达到最低值7713.6元,低于双模式的排放成本7727.7元(如图中水平虚线所示)。共享停车费和共享电动汽车时变租赁费用组合定价与系统交通排放成本之间的关系见表2所示,也就是“共享电动汽车+共享停车位”并不是总能降低系统交通排放成本,只有合理组合优化定价才可以有效减少系统交通排放成本;相反过高或过低的费用组合反而会造成系统交通排放成本的快速上升,甚至高于双模式的系统交通排放成本。

表2 共享停车费用和共享电动汽车时变租赁费用组合定价对系统交通排放成本的影响Table 2Total emission cost under different levels of the combinational pricing

7.1.2 共享电动汽车时变租赁费用与共享停车费对交通拥堵的影响

由于拥堵排放是交通污染排放的重要组成部分,因此本文进一步分析组合定价与交通拥堵之间的关系,而平均排队时间AQT反映了瓶颈路段的交通拥堵程度,因此图4给出了组合定价与平均排队时间的变化关系。图中实线为多模式均衡下的平均排队时间,虚线为双模式均衡下的平均排队时间。

图4 共享停车费用和时变租赁费用对平均排队时间的影响Figure 4Average queuing time under different levels of the shared parking fee and time-dependent fee

多模式下的平均排队时间均小于双模式的平均排队时间,同时多模式下平均排队时间随共享电动汽车时变租赁费用η的增加先减小后增加。因此增加SEV+SP作为补充出行方式,系统均衡时相比于双模式能够减少平均排队时间,即减少拥堵。例如,多模式均衡时,当共享停车费用τ为5元/次,在时变租赁费用η为0.5元/小时,平均排队时间达到最低值0.9小时;共享停车费用τ为3元/次,在时变租赁费用η为2.5元/小时,平均排队时间达到最低值0.73小时,也就是共享停车费τ越小,系统的平均排队时间最低值越小。多模式下的平均排队时间均明显小于双模式的平均排队时间(1.1小时)。

结合表2和图4可以发现,当平均排队时间最小时,系统并未达到最低的系统交通排放成本TEC,例如当共享停车费τ为4元/次,时变租赁费用η为1.5元/小时,虽然平均排队时间最小,但是系统交通排放成本较大。

7.1.3 共享电动汽车时变租赁费用与共享停车费对社会效益和系统交通排放成本的影响

图5是多模式均衡下社会效益TR(图中点画线)及系统交通排放成本TEC(图中实线)与共享停车费τ和时变租赁费用η的关系图。随着时变租赁费用的增加系统交通排放成本先减小后增大,而社会效益先增大后减小。增加SEV+SP出行模式,当系统均衡时,相比于双模式(图中加粗水平虚线为双模式下的社会效益,10280元)一定会增加社会效益,但不一定会降低系统交通排放成本(图中较细水平虚线为双模式下的系统交通排放成本,7727.7元)。例如,共享停车费用τ为3元/次,时变租赁费用η为1.6元/小时,取得社会效益的最大值为10632元。共享停车费用τ越小,时变租赁费用η也较小时,取得的社会效益值较大。

图5 共享停车费用和时变租赁费用对系统交通排放成本(左侧纵坐标)与社会效益(右侧纵坐标)的影响Figure 5Total emission cost (left ordinate) and total revenue (right ordinate) under different levels of the shared parking fee and time-dependent fee

当社会效益最大时,系统无法同时取得最低的系统交通排放成本。当共享停车费用τ一定时,使社会效益最大的时变租赁费用η低于使系统交通排放成本最小的时变租赁费用η。因此,如果为了取得更高的社会效益,应该设置较低的时变租赁费用η,并且降低共享停车费用τ;如果为了减少系统交通排放成本,则应该设置较大的时变租赁费用η,和较小的共享停车费τ。本文将进一步讨论如何组合定价共享电动汽车的时变租赁费用η和共享停车费用τ,才可以兼顾系统交通排放成本和社会效益。

7.2 含有权重w情况下的最优组合定价

本文为了达到同时最大化社会效益TR和最小化系统交通排放成本TEC的目的,采用评价函数法,令w为社会效益的权重,1-w为系统交通排放成本的权重,将双目标优化模型转化为单目标优化模型,如公式(23)所示,并进一步求解在多模式交通路网中,系统均衡时共享电动汽车时变租赁费用和共享停车费用的组合优化解。

在不同的权重w下,使系统最优的共享电动汽车时变租赁费用和共享停车费最优组合定价如表3所示。其中,最优时变租赁费用取较高值η∗∈[7.08,8],最优共享停车费用取较低值τ∗∈[0,1.8]。随着权重值w的增加,即管理者对于社会效益TR的重视程度提高,应当合理降低共享电动汽车的时变租赁费用η和共享停车费用τ,从而增加共享电动汽车用户的数量。随着w的减小,也就是管理者对于系统交通排放成本TEC的重视程度增加,此时提高共享停车费用τ,从而减少共享电动汽车用户数量。但是当w≥0.75以后,由于系统均衡已经稳定,共享电动汽车数量不会继续增加,最终稳定在136辆。因此再进行组合费用的调节就失去了意义,如图6。

表3 权重w变动时最优组合定价Table 3The optimal combinational pricing against the weight

由图6可知,随着权重值w的增加,即管理者对于社会效益的重视程度增加,对于排放的重视程度降低,共享电动汽车的数量逐渐增多至136辆。在w=0,也就是管理者对于系统交通排放成本TEC的重视程度最高、对于社会效益TR的重视程度最低,共享电动汽车的数量为27辆,大于0。由此可见,适当地引入SEV+SP模式比传统的双模式,可以有效地减少平均排队时间AQT,从而减少了由于拥堵造成的污染排放,见图3所示。因此以减少系统交通排放为目的,引入共享电动汽车是一种可行方式,但是不应无限制的鼓励。

图6 权重变动时最优组合定价对应的共享电动汽车数量Figure 6Variation of the number of shared electric vehicles corresponding to the optimal combinational pricing against the weight

图7给出了在权重w不同的情况下,社会效益TR与系统交通排放成本TEC的变化趋势。可以看出随着权重值w的增加,系统中共享电动汽车的数量逐渐增加,因此社会效益上升,与此同时系统交通排放成本也增加,且权重值w越大系统交通排放成本的增加越显著。当权重小于0.2时,系统交通排放成本和社会效益均增长缓慢;当权重在0.2到0.45时,系统交通排放明显增加;当权重大于0.6时,系统已经产生了大量的排放。因此如果一味地重视社会效益,鼓励更多的SEV+SP出行模式,会导致系统交通排放成本迅速增加。建议管理者在鼓励SEV+SP共享出行模式时,应充分考虑交通系统的通行能力,从减少交通排放的角度,选取较小的权重指标,建议w≤0.2。

图7 权重变动时最优组合定价对应的社会效益和系统交通排放成本Figure 7Variation of total revenue and total emission cost corresponding to the optimal combinational pricing against the weight

8 结论

本文在原有的私有小汽车和公共交通双模式出行的基础上,提出了SEV+SP出行模式。以早高峰城市中心区域的办公建筑物和毗邻居住区为案例,基于瓶颈经济学理论分析了考虑带权重的系统交通排放成本和社会效益双目标优化模型时,共享电动汽车的时变租赁费用和共享停车位的停车费用的组合定价优化问题。

研究结果发现早高峰时段城市中心区域,引入SEV+SP作为出行模式的一种补充,通过对共享电动汽车的时变租赁费用和共享停车费用组合定价的优化,相比于双模式而言恰当的组合定价可以达到降低系统交通排放成本,减少交通拥堵,并增加社会效益的目的。虽然引入共享电动汽车是一种可行方式,但是不应无限制的鼓励。其次本文发现通过组合定价共享电动汽车时变租赁费用η和共享停车费用τ,可以影响SEV+SP模式的出行数量,从而有助于达到不同的社会目标。①合理组合优化共享电动汽车的时变租赁费和共享停车费,可以有效减少系统交通排放成本,相反过高或过低的费用组合反而会造成系统交通排放成本的快速上升,甚至高于双模式的系统交通排放成本。②增加SEV+SP作为补充出行方式,相比于双模式能够显著减少平均排队时间,也就是减少拥堵。③共享停车费用的定价越低,取得的社会效益越高,在共享停车费用一定时,较低的时变租赁费用也有助于获得更高的社会效益。④如果同时最大化社会效益,最小化交通排放,建立带权重的双目标优化模型,使得系统最优的时变租赁费用应取较高值,共享停车费用应取较低值。⑤如果一味地重视社会效益,鼓励更多的SEV+SP出行模式,会导致系统交通排放成本迅速增加,建议管理者在鼓励SEV+SP出行模式时,应充分考虑交通系统的拥堵压力,从减少交通排放的角度,应选取较小的权重指标w,建议小于0.2。

本文分析了综合考虑系统交通排放成本和社会效益的SEV+SP出行模式的组合定价问题,今后的研究还可以从多个方面拓展,例如:完善可预约的共享停车制度,保证车位预约的准确性、可靠性;其次,共享车位的布设是否能够满足需求,电动车充电桩的设置是否满足需求与经济性的要求;另外,共享车位是否仅能供共享电动汽车预约使用,私有小汽车用户能否也通过预约的方式使用;最后,是否能够有部分共享电动汽车用户通过提早出发,提早或准时到达目的地。