基于3D打印的三维短纤维增强复合材料强度预测分析
2022-01-17李凌岩周金宇马馨远
李凌岩,周金宇,马馨远
(1.江苏理工学院机械工程学院,江苏常州 213001; 2.金陵科技学院机电工程学院,南京 211100; 3.同济大学汽车学院,上海 201800)
短纤维增强树脂基复合材料由短纤维和树脂基体按照一定的配比混合而成,随机分布的短纤维是复合材料的主要成分,是承受载荷的重要部分,树脂基体则保持复合材料的完整性。短纤维增强复合材料具有比强度高、比刚度高、抗疲劳性能好、耐腐蚀、可设计性高等众多优点,被广泛用于航天航空、汽车、船舶、风电等领域。短纤维增强复合材料微观结构错综复杂,科学准确地预测出短纤维增强复合材料的力学性能对短纤维增强复合材料的广泛应用、改善设计和减少材料浪费具有里程碑的意义。目前,绝大多数情况下都是采用实验方法测试短纤维增强复合材料的力学性能,需要大量的时间和成本,且缺乏物理内涵,因此建立三维随机分布短纤维增强复合材料强度理论预测模型尤为重要。
短纤维增强复合材料的强度预测是复合材料领域研究的重点之一。Kelly等[1]和Bowye等[2]提出的修正混合律模型是预测非连续纤维增强复合材料强度的两个常用模型。Fukuda等[3]采用概率的方法研究纤维长度和取向分布对短纤维增强复合材料强度的影响。Zhu等[4]考虑纤维和基体位移变形的不均匀性、残余应力、纤维弥散强化和基体中错位密度等因素,提出了一种分析随机取向短纤维增强复合材料强度的模型,用于预测复合材料强度。张立群等[5]首次基于Cox剪滞法和复合材料结构特点研究了橡胶/短纤维复合材料在较宽纤维体积和长度范围内的拉伸强度规律,提出了新的混合规律来预测橡胶/短纤维复合材料的纵向拉伸强度[6–10]。
至今为止,对短纤维增强复合材料的强度理论预测仍然处于探索阶段,绝大多数的预测仍以实验和二维平面预测为主,但随着3D打印技术的快速发展,纤维取向在三维空间内的制造成形已成为可能,故笔者考虑临界区域内短纤维取向、长度和体积分数等因素建立三维短纤维增强复合材料强度预测模型,可以节省大量的时间和成本,更好地应用于航天航空、军工等领域[11–15]。
1 短纤维增强复合材料强度预测模型
1.1 混合律模型
混合律模型通常用来预测单向连续纤维增强复合材料的强度,认为纤维和树脂基体为等应变,混合律模型计算公式如式(1)所示。
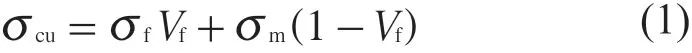
式中:σcu——复合材料强度;
σf——纤维强度;
σm——树脂基体强度;
Vf——纤维的体积分数。
若材料为单向不连续的短纤维增强复合材料,式(1)可以修正为式(2)和式(3)。
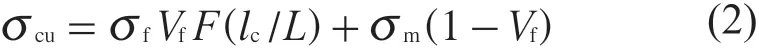
式中:lc——纤维的临界长度,是指纤维增强复合材料中刚能使材料具有原纤维拉伸强度时的纤维长度;
L——纤维的平均长度。

lc可根据文献[16]求得,如式(4)所示。

式中:d——纤维直径;
τy——树脂基体的剪切强度。
可根据文献[17]求得树脂基体的剪切强度,如式(5)所示。

1.2 临界区域及概率理论
Fukuda等[3]在预测单向短纤维增强复合材料的强度时提出了“临界区域”的概念。临界区域由一对垂直于加载方向相距βL的平面确定,β为临界区域系数,0≤β≤1。如果纤维贯穿临界区域宽度则称为桥接纤维,如果纤维的末端位于临界区域内,则称为终止纤维。终止纤维对该区域不能起到增强作用,其强度相当于树脂基体强度。图1为短纤维的分类及表示。如图1a所示,1,2,3为终止纤维,4为桥接纤维;如图1b所示,长度为l的短纤维在空间各轴上的长度如式(6)所示。

式中:lx——长度为l的纤维x轴的长度;
ly——长度为l的纤维y轴的长度;
lz——长度为l的纤维z轴的长度;
θ——纤维与z轴夹角;
φ——纤维与x轴夹角。
如图1c所示,长度为l的短纤维的临界角θc满足式(7)。

若β>1,θc无法定义,纤维为终止纤维;若纤维的欧拉角θ为大于临界角度的锐角,纤维为终止纤维。若0≤β≤1且纤维取向角小于临界角度时,纤维为终止纤维的概率为临界区域宽度与纤维在临界宽度方向上长度值之比。那么长度为l,欧拉角为θ的单根纤维为终止纤维的概率Pe由式(8)计算。


单根桥接纤维概率Pb由式(9)计算。

由式(8)、式(9)可知桥接纤维和终止纤维的概率可用β来表征。考虑纤维取向分布的不确定性,引入短纤维取向的概率密度函数g(θ),f(φ)满足式(10)和式(11)。
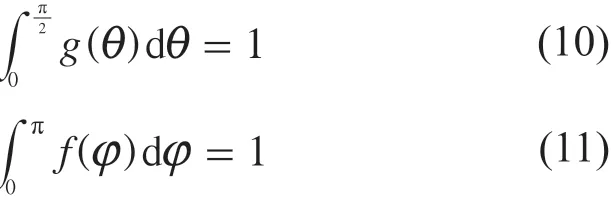
1.3 短纤维的应力分布
图2 为短纤维应力分布图。根据图2,由式(12)得纤维的平均拉伸应力σf0。

图2 纤维应力分布简化图

式中:σf(z)——平行于拉伸应力方向上的纤维应力分布函数。
图3 位欧拉角为θ,φ的纤维施加应力情况。如图3所示,当短纤维与z轴成夹角θ,与x轴成夹角φ时,沿z轴施加拉力σ0,根据三维应力转轴公式得沿短纤维方向上正应力σ0′,如式(13)所示。

图3 欧拉角为θ,φ的纤维施加应力情况

忽略剪应力和横截面积变化的影响,则纤维在拉伸方向上的载荷Fz如式(14)所示。

式中:Af——纤维的横截面积。
1.4 随机取向短纤维增强复合材料的强度预测
假设短纤维增强复合材料试件为长方体,长方体的边长分别为a,b,c,且c与x轴平行,那么纤维体积分数Vf可表示为式(15)。

式中:N——纤维的总数。
纤维在z轴的平均长度Lz由式(16)计算。

若NLz为所有纤维在z轴上的总长度,那么用总长度除以试件的长度c,得试件中垂直于x轴截面的纤维平均数Nc如式(17)所示。
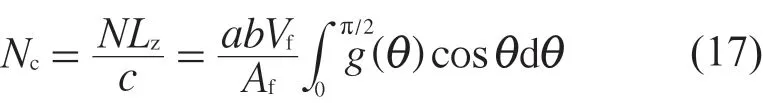
假设临界区域内纤维体积分数不变,求得截面内任意纤维为终止纤维和桥接纤维的概率qe和qb,如式(18)和式(19)所示。

那么截面内终止纤维数Ne和桥接纤维数Nb表示为式(20)和式(21)。

由于Ne只是根据一个截面求得并不精确,鉴于以下计算仅用到桥接纤维的数量,故在后续计算中不考虑Ne的影响。由式(14)可求临界区域内桥接纤维所受z方向的载荷Fb,如式(22)所示。

由式(23)求得所有桥接纤维在z方向的载荷FT。

由于终止纤维对材料不能起到增强作用,故其强度相当于基体强度,由式(1)可知短纤维增强复合材料的强度σcu包括桥接纤维强度、终止纤维强度和树脂基体的强度,故可得式(24)。

当l≥lc时,可得式(25)。
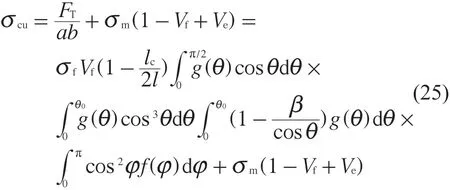
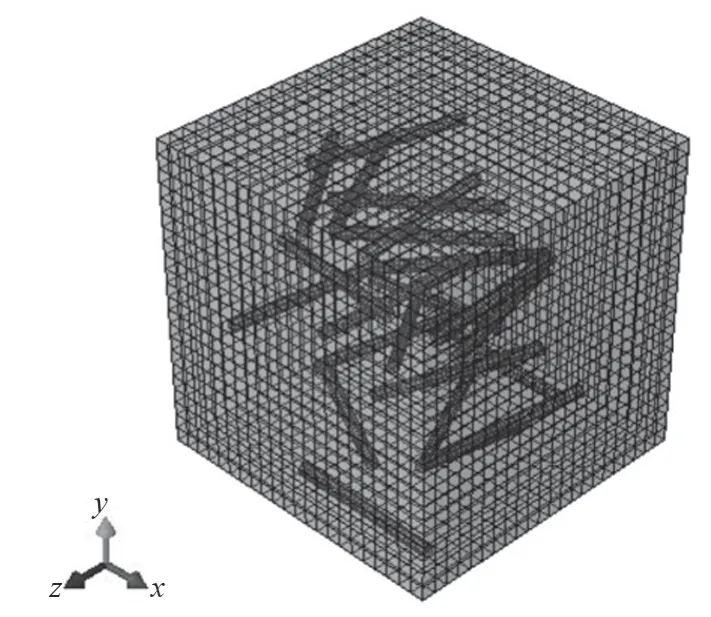
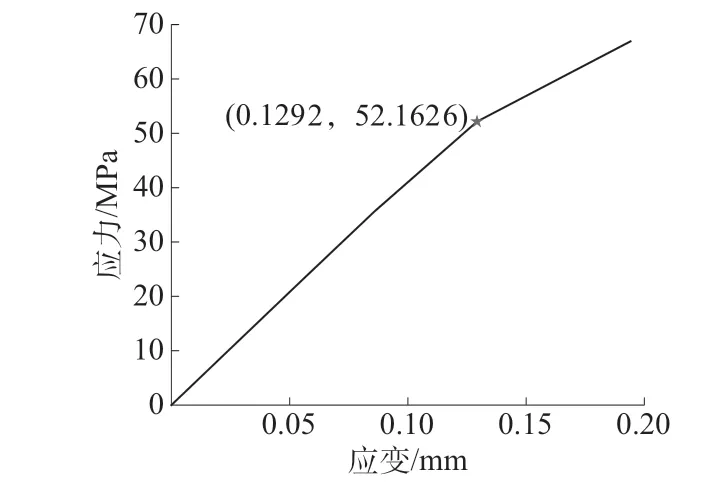
当l 为验证建立的理论模型,以短碳纤维增强尼龙复合材料进行理论预测、仿真分析和拉伸试验。短碳纤维、尼龙材料各自性质参数列于表1、表2。 表1 碳纤维性质参数 表2 尼龙性质参数 短纤维的欧拉角θ,φ概率密度函数公式分别如式(27)和式(28)所示。 采用随机序列吸附法(RSA)来数值生成随机分布的短纤维增强复合材料的几何结构。采用RSA时,逐个将位置和取向都随机的短纤维添加到树脂基体中。在三维空间内将短纤维设为圆柱体。首先根据指定函数随机生成纤维中心点C(x0,y0,z0),其次根据式(27)、式(28)生成取向角θ,φ,最后由纤维半径r和纤维长度l生成三维短纤维,将生成的纤维逐渐加入到树脂基体中,保证新加入的纤维不能与之前树脂基体已接受的纤维相交,直到满足纤维体积分数条件,流程图如图4所示。 图4 短纤维增强复合材料建模流程图 利用RSA分别生成尺寸为200 μm×200 μm×200 μm,纤维体积分数为5%,10%,15%,20%的短纤维增强复合材料模型,其中纤维直径为7.5 μm,纤维长度为100 μm。短纤维增强复合材料的短纤维增强相和树脂基体相的几何数据通过Matlab程序生成,利用Python脚本文件导入有限元软件Abaqus中。纤维体积分数为5%的短纤维增强复合材料模型如图5所示。 图5 有限元模型图 在Abaqus中对短纤维增强复合材料模型进行网格划分,如图6所示。 图6 划分的网格图 利用有限元软件Abaqus仿真,通过对短纤维增强复合材料模型的z轴一端施加应变ε=0.01,另一端进行6个自由度全约束,并创建参考点(与模型建立相应的耦合关系)进行仿真分析。在后处理中,输出参考点的力-位移曲线转化为参考点的应力-应变曲线,即短纤维增强复合材料z轴的等效应力-应变曲线。短纤维增强复合材料应力云图如图7所示。 图7 模型应力云图 从应力云图中可以看出短纤维是复合材料中主要承载组分,基体只是起到传递力的作用。图8是短纤维增强复合材料z轴等效应力-应变曲线,从图8可以看出曲线呈双线段特征,应力达到一定值时,曲线开始转折,折点即短纤维增强复合材料失效的起始点,故此点的应力值为短纤维增强复合材料的初始失效强度,即52.162 6 MPa为纤维体积分数为5%的短纤维增强复合材料强度值。 图8 短纤维增强复合材料模型等效应力-应变图 利用熔融沉积成型3D打印技术,打印出不同体积分数的短纤维增强尼龙复合材料试样,试样尺寸如图9所示。 对试样进行测试前,需使用AB胶在试样两端粘贴加强片,如图10所示,加强片的材质一般选为铝片,厚度为2 mm,粘贴加强片前,需使用砂纸对粘贴表面进行打磨,粘贴加强片后,要立即对试样粘结表面加压力(一般为12 h左右)。 图10 试验试样示意图 通过美特斯工业系统(中国)有限公司的MTS810型万能试验机完成试样力学性能测试。打印件拉伸测试前,装夹固定在万能试验机两端,如图11a所示。以1.5 mm/min的速度进行拉伸,直到成型件断裂,如图11b所示。 图11 试件的装夹和断裂 根据理论建立的三维短纤维增强复合材料强度预测模型、有限元软件和拉伸试验对不同纤维体积分数的短纤维增强复合材料的z轴强度进行分析,结果如图12所示,相应误差分析见表3。 图12 不同纤维体积分数短纤维增强复合材料强度分析 表3 不同纤维体积分数短纤维增强复合材料强度分析的误差 % 从图12及表3可以看出,理论预测值与有限元Abaqus仿真分析值相差不大,由于个体制造差异、试验操作方面的误差以及试验环境的变化,理论预测值与拉伸试验值存在一定的差异,但不同体积分数纤维随机分布的三维短纤维增强复合材料强度理论预测值与拉伸试验值的误差均小于10%,在允许范围内,且理论预测值比有限元仿真值更接近试验值,验证了三维短纤维增强复合材料强度预测模型准确性。 (1)通过修正混合律模型以及结合三维短纤维空间几何特性,基于概率方法综合考虑纤维取向、长度和体积分数提出了基于3D打印的三维短纤维增强复合材料的强度预测模型。 (2)对建立的模型进行验证。利用Matlab生成随机短纤维和基体的几何数据通过Python脚本导入有限元分析软件Abaqus中进行仿真分析,发现理论预测值与仿真分析值误差小于10%。通过3D打印技术打印试件进行拉伸测试,理论预测值与拉伸试验值误差小于10%,且比仿真结果更加接近试验值,表明建立的三维短纤维增强复合材料强度预测模型科学合理。 (3)对三维短纤维增强复合材料强度进行预测,能为短纤维增强复合材料3D打印件的设计与制造提供理论指导。按需控制纤维取向、长度和体积分数使复合材料的力学性能满足实际工程需要,更好地实现短纤维增强复合材料在航天航空、汽车、船舶、风电等领域的轻量化设计和应用。
2 算例分析



2.1 短纤维增强复合材料细观建模

2.2 短纤维增强复合材料的数值仿真


2.3 短纤维增强复合材料3D打印件拉伸测试


2.4 结果分析


3 结论
