抑制闭环光纤陀螺高动态角运动测量误差的校正回路设计

张桂才，冯 菁，宋凝芳，林 毅，罗 巍，杨 晔,2

（1. 天津航海仪器研究所，天津 300131；2. 中国船舶航海保障技术实验室，天津 300131；3. 北京航空航天大学，北京 100191）

光纤陀螺在惯性导航、控制和测量领域已经得到广泛应用[1-5]。尽管如此，由于目前闭环光纤陀螺控制回路存在固有延迟和非线性解调环节，会产生一定程度的振动零偏效应。这是由于陀螺闭环反馈回路的瞬态残余误差信号较大导致解调非线性引起的振动误差。本文作者曾就回路固有延迟引起的信号超调，提出通过约束回路增益来降低振动零偏效应，并在工程实践中得到应用[6]，但这种方法也在一定程度上限制了光纤陀螺带宽。在某些大动态应用中将产生较大的角速率跟踪误差，影响系统精度。

本文针对车载冲击颠振环境中应用的捷联式惯性测量单元（IMU）的光纤陀螺反馈控制回路传递函数进行建模分析，提出一种采用回路校正技术进一步抑制残余误差信号的方法。研究表明，该技术可以在抑制振动零偏效应的同时将陀螺角速率跟踪误差以及最大瞬态角误差降低一个数量级以上，为提高光纤陀螺的恶劣动力学环境适应性提供技术途径。

1 闭环光纤陀螺传递函数的建模和分析

1.1 闭环光纤陀螺的物理模型和传递函数

闭环光纤陀螺的控制回路在载体加速和减速过程中的跟踪误差无法从陀螺的输出中直接观察到和分离出来，因而很难对其进行标定和补偿。通过对光纤陀螺传递函数进行建模，可以从理论上分析这类误差的产生机制，并进而对系统性能进行评估和预测。

通常将光纤陀螺闭环回路划分成几个独立的环节，分别给出每个环节的传递函数，再根据这些环节在陀螺中的控制衔接关系，推导出光纤陀螺闭环传递函数。光纤陀螺通过测量两束反向传播光波之间的非互易相位差来敏感载体的旋转角速率，控制回路主要由Sagnac干涉仪、光探测器、前置放大器、A/D转换器、多点采样与解调器、一次积分、数字截取、二次积分、D/A转换、驱动放大器、相位调制器、线圈延迟等环节组成[7]，其中模拟电子元件产生的延迟很小，可以忽略，因此系统中最主要的延迟是数字寄存器和数字处理器处理时序产生的延迟，这些延迟一般为光纤环传输时间τ的2至4倍。忽略采样和解调等非线性环节，未经校正的光纤陀螺闭环控制回路的典型传递模型如图1所示[7,8]。归一化后的传递函数可以表示为：

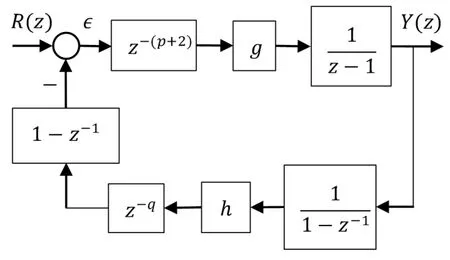
图1 闭环光纤陀螺的结构图Fig.1 Structure diagram of closed loop FOG

式中g、h分别为光纤陀螺控制回路的前、后向通道增益，p、q分别表示前、后向通道的固有延迟。

1.2 约束回路增益抑制振动零偏效应

振动零偏效应是反映光纤陀螺动态适应性的一项重要指标，它表现为振动过程中陀螺零偏（均值）发生偏移。振动零偏效应与光纤陀螺的调制/解调原理及其参数设计有关。通常光纤陀螺通过Sagnac效应敏感角速率，然后产生一个施加到相位调制器上的反馈信号，使偏置工作点保持恒定。但是由于回路延迟，反馈信号总是会滞后于Sagnac相位，形成残余误差信号。该误差在回路刚度不足时的高动态输入下会变得很大。通常，当光纤陀螺工作在过调制状态及瞬时残余误差信号很大时，如图2所示，由于光/电余弦响应的非线性，正负解调周期的采样值将不对称，使得解调环节的增益变为与输入同频的时变参量，这称为广义的探测器饱和，将导致振动零偏效应[6]。

图2 余弦响应非线性引起的广义探测器饱和Fig.2 Generalized detector saturation caused by cosine response nonlinearity

研究表明，对于图1所示含有固有延迟的闭环光纤陀螺，当回路开环增益过大时，回路输出会出现超调，将进一步放大上述振动零偏效应。考虑图2存在的非线性解调环节，可以通过降低回路增益来抑制振动零偏效应，并改善稳定裕度。图3给出了光纤长度为1500m的某型陀螺在回路固有延迟为4τ时，振动零偏效应与回路增益的函数关系，可以看出，要将振动零偏误差控制在0.01°/h以下，需要将回路增益限制在gh=0.03以内，相应的带宽约为：

图3 振动零偏效应与回路增益的关系Fig.3 Relationship between vibration bias effect and loop gain

式中fp为光纤环圈的本征频率，。此时光纤陀螺的带宽约800Hz，这种方法本质上是通过牺牲陀螺的动态响应范围来换取振动零偏误差的降低。

1.3动态输入下的角速率跟踪误差和瞬态角误差

参照文献[9]，我们把陀螺仪的角运动测量误差定义为在某一时刻对输入角速率变化的跟踪误差的积分，也即瞬态角误差。对于本文关注的车载冲击振动条件，要求光纤陀螺在特定角速率分布下的最大瞬态角误差为几个微弧度。在图1所示的实际闭环光纤陀螺的传递模型中，回路延迟4τ，将回路增益约束至gh=0.03水平，我们仿真发现，其频率特性与不含延迟的具有同样增益的一阶惯性环节近似。因而，对于以角加速度α运动的载体，很容易得到校正前陀螺的稳态角速率跟踪误差为：

图4是某型闭环光纤陀螺输入角速率斜坡信号时的系统响应，其中局部放大的区域为加速开始前后共2ms阶段的输入和输出响应，可以看出，此时输出相较于输入有一个较大的角速率跟踪误差。其中，光纤长度为1500 m时，光纤环传输时间为τ=7.5×10-6s。设输入角速率在加速和减速时的角加速度分别为±100°/s2，角速率跟踪误差和瞬态角误差如图5所示，可以看出，加速或减速过程的角速率跟踪误差达到ΔΩ≈423μrad/s ≈ 87°/ h ，虽然在7s的整个工作过程中的累积角误差基本为零，但2s时的瞬态角误差已达到430μrad。这说明，因抑制振动零偏效应而约束回路增益引起的光纤陀螺带宽下降，导致较大的角速率跟踪误差和瞬态角误差。在仿真中，尽管载体通过加速或减速改变运动状态后又回到原状态，整个动态过程上角速率跟踪误差引起的累积角误差在一阶上很小或为零，但某个时刻的瞬态角误差可能较大，不能满足高机动性IMU的角运动测量精度要求。

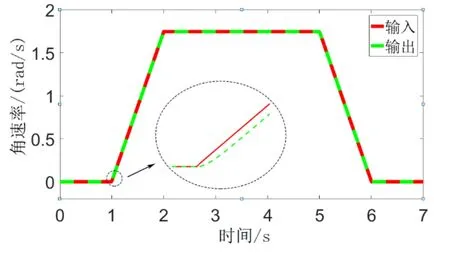
图4 标准控制回路的斜坡信号响应Fig.4Slopesignal response of standard control loop

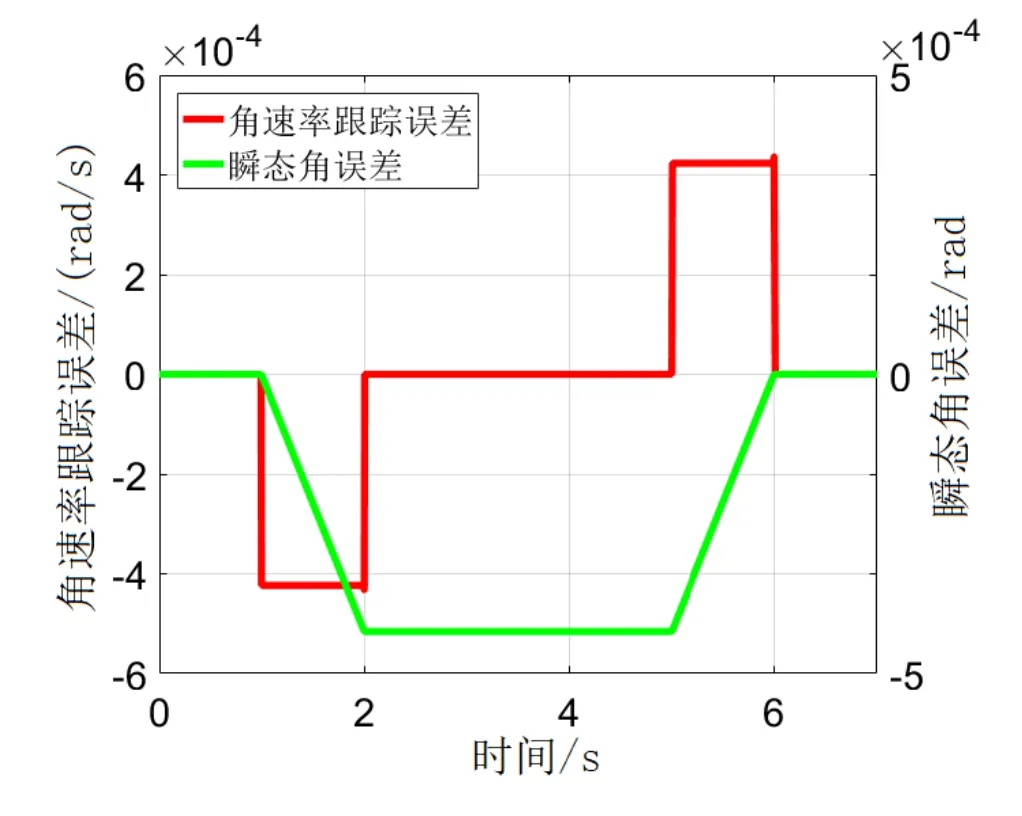
图5 标准控制回路的角速率跟踪误差及瞬态角误差Fig.5Angular rate tracking error and transient angular error of standard control loop

2闭环光纤陀螺的回路校正设计

2.1高机动应用下回路校正的必要性

据上所述，对于大动态应用条件，有必要改进光纤陀螺的闭环控制回路。本文尝试采用回路校正技术来使振动零偏效应和角速率跟踪误差同时满足系统的动态性能要求。目前在这方面的文献报道和可资借鉴的成熟方案很少。文献[10]针对闭环光纤陀螺的振动零偏效应，基于数字控制系统的有限拍无差设计，提出了一种回路校正方案，对残余误差信号进行高阶补偿，理论上可将残余误差信号抑制两个数量级以上。但该文献没有考虑回路延迟对闭环光纤陀螺系统稳定性的影响，因而虽然对残余误差信号的补偿效果理想化，但设定的增益参数不合理，计算后发现系统的稳定裕度不够。文献[9]针对减小动态输入下的角速率跟踪误差及瞬态角误差，仍然基于最少拍控制原理，在陀螺的标准闭环控制回路中增加了一个与串联回路并联的一个附加积分路径，通过蒙特卡洛仿真证明导航精度有了实质的改进。该文献虽然意识到回路延迟的影响适当调整了增益参数，但其最少拍设计基于精准的回路总延迟，这在实际设计中难以实现。

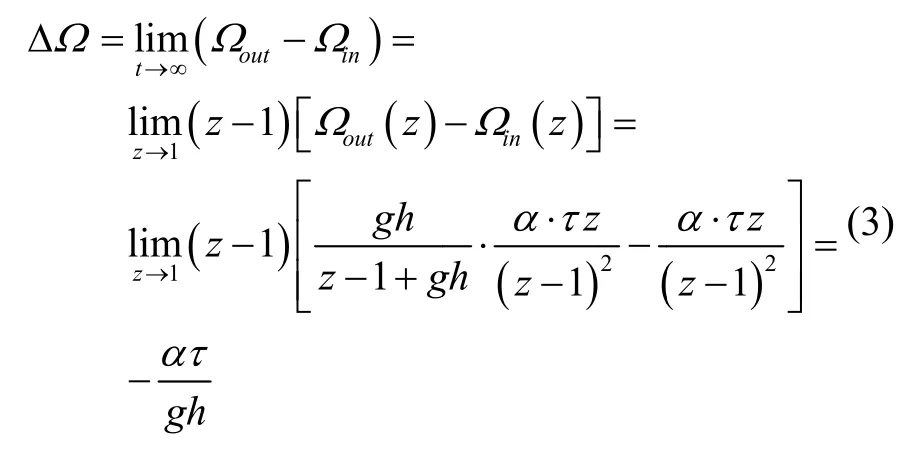
因此，本文基于自控理论的比例-积分控制规律提出了一种改进的闭环光纤陀螺的回路校正方案，即在回路中增加PI控制器。

校正前的系统包含有两个积分环节，但由于后向通道中包含有一个线圈延迟环节，可与其中一个积分环节相抵消，故系统近似为Ⅰ型系统。其静态速度误差系数为有限值，故输入为斜坡信号时，速度误差不为零。而PI控制器相当于在系统中增加了一个位于原点的开环极点和一个负实开环零点。该极点可以提高系统的型别，使速度误差为零，而增加的负实零点可以缓和PI控制器的开环极点对系统稳定性及动态过程产生的不利影响。与文献[9][10]相比，本文给出的回路校正方案中不仅减小了系统的残余误差信号（抑制振动零偏效应），提高了光纤陀螺的闭环带宽，而且确保了陀螺的稳定性能，降低了动态输入下的角速率跟踪误差。

2.2 闭环反馈控制回路的校正设计和传递函数

本文在串联回路中并联了一个起校正作用的积分路径。带校正回路的闭环光纤陀螺结构如图6所示，其中k为校正系数，mτ为积分环节中的时间延迟。研究表明，增大k可以提升系统的响应速度，但k过大会使系统传递函数的幅频特性存在明显谐振峰，进而导致振动零偏效应，因此k不宜大于0.003。增大系统回路增益gh可以提升系统的动态性能，增大系统带宽，但gh过大会使系统稳定裕度变差，因此gh不宜大于0.09。此外，改变m同样会影响系统传递函数的幅频特性，综上考虑，选取gh= 0.09,k= 0.002,m=1。增加校正后的系统传递函数可以表示为：

图6 带校正的闭环光纤陀螺结构图Fig.6 Structure diagram of closed loop FOG with correction

3 增加回路校正的仿真结果

3.1 增加回路校正的频率特性和稳定裕度分析

在gh= 0.09,k= 0.002,m=1的情况下，增加校正回路前后陀螺的幅频特性曲线如图7所示。从图中可以看出，增加校正回路后，陀螺闭环带宽由约800 Hz增加为3600 Hz左右，且幅频特性曲线无明显谐振峰。

图7 校正前、后传递函数幅频特性曲线Fig.7 Amplitude frequency characteristic curve of transfer function before and after correction

利用Simulink仿真对增加校正后的闭环光纤陀螺的稳定性进行分析，求得增加校正回路后的幅值裕度和相角裕度分别如表1所示。校正后系统的裕度满足自控理论中对系统稳定性的要求，即幅值裕度应大于6dB，相角裕度应大于30 °。

表1 幅值裕度和相角裕度Tab.1 Amplitude margin and phase margin

3.2 动态输入条件下的角速率跟踪误差仿真

对于某型光纤陀螺，增加校正回路后系统对特定输入的响应如图8所示，图8中子图为加速开始前后共4 ms内输出响应的局部放大，从此子图中可以看出，虽然系统的响应时间变长，但角速率跟踪误差明显减小。角速率跟踪误差及瞬态角误差如图9所示。图8中，加速或减速过程的角速率跟踪误差 ΔΩ≈ 13μrad/s ，比校正前减小了一个数量级以上。对应的最大瞬态角误差为6.99 μrad，同样比校正前减小了一个数量级以上，满足车载冲击振动条件下最大瞬态角误差为几个微弧度的角运动测量误差需求。

图8 增加校正后回路的斜坡信号响应Fig.8 Slope signal response of corrected loop

图9 增加校正后系统的角速率跟踪误差及瞬态角误差Fig.9 Angular rate tracking error and transient angular error of the corrected system

4结论

对于车载冲击振动条件下的某些应用，要求光纤陀螺在特定角速率分布下的最大瞬态角误差为几个微弧度。实际中，由于陀螺标准闭环控制回路存在固有延迟，为避免超调和振动零偏效应，必须约束回路增益。针对特定输入信号，实际计算证明，标准控制回路的最大瞬态角误差并不能满足系统级几个微弧度的角运动测量误差的要求。本文提出了一种回路校正技术作为基本的解决方案。

针对光纤长度为1500 m的某型光纤陀螺，对增加校正后的光纤陀螺闭环控制回路进行了仿真分析，结果表明，增加回路校正设计后可以将光纤陀螺的带宽提高为原来的四倍，且没有过分削减陀螺的稳定裕度。对于特定输入信号而言，角速率跟踪误差和最大瞬态角误差均比校正前减小了一个数量级以上，角运动测量误差大大降低，满足车载冲击振动条件下的角运动测量精度要求。