一种单偏振低噪声谐振式空芯光子晶体光纤陀螺

申河良，毕 然，傅 力，佘 玄，陈 侃，舒晓武

（1. 浙江大学光电科学与工程学院，杭州 310027；2. 光迅科技股份有限公司，武汉 430205）

近年来，随着各种海陆空天惯导航姿系统的发展，对惯性器件在轻型微小化、高集成度、测量精度等方面提出越来越高的要求。谐振式光纤陀螺（Resonator Fiber Optic Gyro, RFOG）通过检测光纤谐振环中顺逆两个方向的谐振频率差来测量角速度。在同等精度下，RFOG所需光纤长度相较于干涉式光纤陀螺可以缩短1-2个数量级。在集成化、小型化、高精度等方面具有优势，是陀螺未来发展的重要方向[1]。光纤谐振腔是RFOG的主要敏感组件，其性能直接影响陀螺精度提升。目前谐振腔多采用传统的实芯光纤绕制，环境温度适应性差，寄生噪声较大，限制了RFOG的精度。空芯光子晶体光纤（Hollow Core Photonic Crystal Fiber,HCPCF）的出现，为RFOG的发展提供了新方向[2]，HCPCF利用周期性结构使得传播光束95%以上的能量位于中央空气中，可大大降低克尔效应、背向散射、温度效应等寄生误差，并且其弯曲损耗小，有利于小型化[3-5]。因此谐振式空芯光子晶体光纤陀螺（HC-RFOG）受到了国内外各研究单位的重点关注。但由于缺少成熟的空芯光子晶体光纤耦合器，限制了RFOG中HCPCF的应用。目前解决这一问题主要有基于熔接型和空间光路耦合型两种方案。

基于熔接耦合的谐振腔有稳定性较好的优点，如浙江大学马慧莲教授课题组采用将HCPCF与传统保偏光纤直接熔接，制作了混合型光纤谐振腔[6]，但HCPCF内部含有空气孔，传统的高温熔接会造成空气孔塌陷导致熔接损耗过大，最终清晰度仅为6.67。

基于空间光路耦合的方案又可分为基于准直系统耦合、硅基自由空间耦合、光波导端面对准耦合三种技术路线。基于准直系统耦合最早由Honeywell提出[3]，其耦合器是由分光片构成的空间耦合结构，HCPCF谐振腔的清晰度达到了42。国内最早由北航搭建并制作陀螺样机，后来发展为采用一对准直器和一系列偏振相关器件构成微光学偏振耦合器，实现了一体化的HCPCF谐振腔[7]，其余如法国Paris-Saclay大学[8]，北京航天时代光电技术有限公司[9]均采用该方法搭建谐振腔。基于准直系统的耦合结构由于采用分立器件，体积较大，稳定性较低，但其优势在于低损耗的耦合可以使谐振腔达到较高的清晰度。

硅基自由空间耦合首先由Honeywell公司提出，其使用高度集成的自由空间硅光学平台来实现腔内光波的低损耗循环和光信号的有效耦合进腔，据报道，该谐振腔的清晰度可达35[10]。此外，采用微加工技术可以将透镜、分束器、偏振器等元件集成在一个硅基平台上，大大提升了系统集成度，但该方案对微纳加工和装配等工艺提出了较高要求。

光波导端面对准耦合最早被斯坦福大学研究人员采用，他们利用微位移机械平台将HCPCF与单模光纤耦合器尾纤进行端面对准耦合，成功搭建了HC-RFOG系统[11]。该方法简单易行，但由于不同光纤之间模场不匹配，导致每个端口的耦合损耗高达2.1 dB。2017年，浙江大学马慧莲教授课题组采用二氧化硅波导耦合器与传统光纤直接对接的方式，搭建了清晰度高达196.7的无熔接点谐振腔[12]，之后他们又报道，该型谐振腔清晰度可以提高到1324[13]，展现了该方案巨大的应用潜力。

受以上各方案的启发，本文提出了一种单偏振低噪声的空芯光子晶体光纤谐振腔，其主要由HCPCF环与退火质子交换铌酸锂（APE-LN）波导耦合器通过端面对准耦合的方式搭建而成。由于传统APE-LN出射光斑分布不对称，因此其与光纤对准时耦合损耗较大（约1 dB）。针对此问题，本文提出利用离子注入和键合技术[14]在APE-LN波导的上表面覆盖一层铌酸锂（LN）材料，从而对APE-LN出射光斑进行改善。通过仿真计算，求得了模斑改善前后的APE-LN波导与HCPCF和传统实芯光纤的耦合效率，给出了该谐振腔的理论极限灵敏度，对HC-RFOG的研究具有一定的参考意义。

1 单偏振低噪声空芯光纤谐振腔的谐振理论

图1为基于HCPCF的单偏振谐振腔结构，耦合端口2与耦合端口3分别与HCPCF环的两端连接，通过端面对准耦合方式与耦合器形成封闭回路，从而形成HCPCF谐振环。耦合端口1和耦合端口2分别连接两根输入实芯光纤1、2，从而保证光波的输入/输出谐振环。

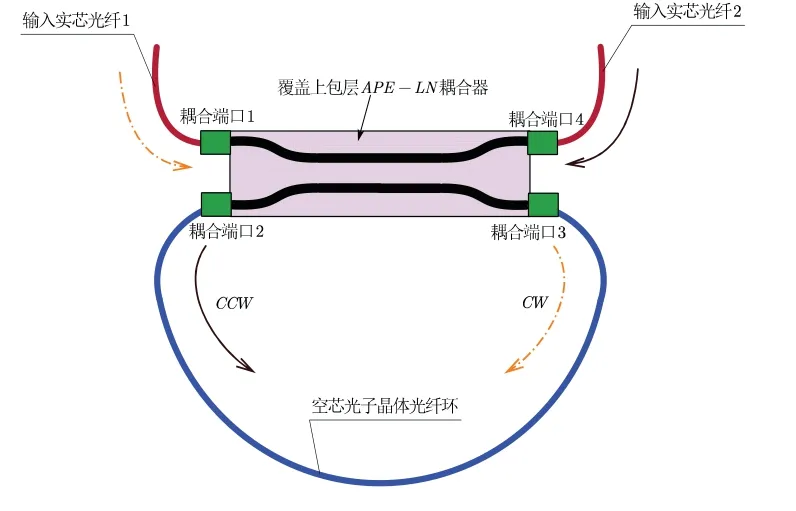
图1 单偏振低噪声空芯光子晶体光纤谐振腔示意图Fig.1 Schematic diagram of the single polarization and low noise HCPCF resonator

图1也显示了该谐振腔的工作原理，以顺时针（Clock Wise, CW）方向传输光波为例，输入实芯光纤1发出光束，经过耦合端口1进入耦合器，采用成熟的退火质子交换工艺制作的LN波导具有极高的消光比（＞60 dB）足以保证腔内光波偏振态保持单一稳定。然后，光波通过耦合端口3进入HCPCF环中。光波沿CW方向在谐振环中传播，经过耦合端口2又进入耦合器，并分为两部分，一部分光波重新经过耦合端口3进入谐振腔，另一部分光波经过耦合端口4输出，如此循环，多次传输后的CW光波被探测器接收。若从耦合端口1入射的光波为：

其中，E0为输入光波光振幅，f0为光源的中心频率，φ0为光源的初始相位。通过光场叠加理论，可以得到：

其中，L为光纤环长，k为耦合器的耦合系数，αs为实芯光纤与波导端面对准耦合损耗，αp为实芯光纤与波导端面对准耦合损耗，αL为空芯光纤传输损耗。β=neff2πf0/c为传播常数，其中neff为纤芯等效折射率，c为真空中光速。若设L=10 m，k= 0.1，αs= 0.5 dB，αp= 0.5 dB，αL=20 dB/km，neff= 1则可给出谐振腔输出光强随入射光波频率的变化曲线，如图2(a)所示。

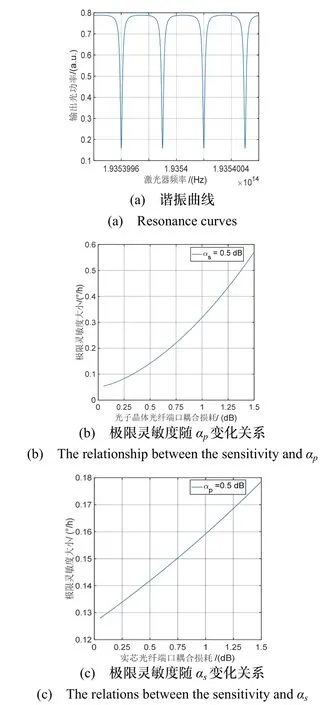
图2 单偏振低噪声空芯光纤谐振腔理论分析Fig.2 Theoretical analysis of the single polarization and low noise HCPCF resonator

对RFOG系统而言，谐振腔的极限灵敏度是极为重要的参数，其表达式为[15]：

其中，A为光纤环面积，λ0为波长，Г为谐振曲线的半高全宽，D为谐振环的直径，F为谐振腔的清晰度，SNR为系统信噪比，由探测器散粒噪声决定的SNR可以表示为：

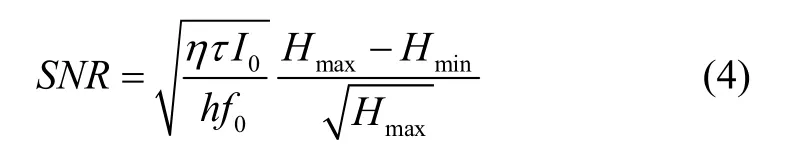
其中，η为光探测器的量子效率，τ为探测器积分时间，I0为输入光功率，h为普朗克常数，Hmax、Hmin分别为谐振曲线的最大值和最小值。

结合理论极限灵敏度表达式(3)，可以分析不同耦合端口的损耗对陀螺性能的影响。若设αs=0.5 dB，λ0=1550 nm，I0=1 mW，D=10 cm，η=0.85，τ=1 s，其余参数与上文一致，空芯光子晶体光纤与波导的耦合损耗αp从0.05 dB增加到1.5 dB时，极限灵敏度变化如图2(b)所示，从计算结果可以看出，极限灵敏度从0.0542 °/h增大到了0.5709 °/h，变化量约为初始值的10倍。相对而言，若设αp=0.5 dB，其余参数保持不变，实芯光纤与波导的耦合损耗αs从0.05 dB增加到1.5 dB时，计算结果如图2(c)所示，极限灵敏度仅从 0.1279 °/h 增大到了 0.1786 °/h，仅增加了0.0507 °/h。以上结果表明，在光纤传输损耗固定的情况下，该谐振腔的极限灵敏度主要由空芯光子晶体光纤与波导的端面对准耦合损耗αp决定，这为下一步谐振腔的设计和参数优化提供了指导。

2 单偏振低噪声空芯光纤谐振腔设计与分析

2.1 覆盖LN上包层的APE-LN建模

降低谐振腔的耦合损耗，从而提升RFOG的性能是本文工作的重点。在光纤与波导理想准直的情况下，影响最大的是模场失配损耗，其次是菲涅尔反射损耗，其中菲涅尔反射损耗可以利用增透膜来降低。最难解决的问题就是如何改善两个模场的失配。耦合效率ξ与模场匹配的关系可以用光纤与波导模场分布的重叠积分来表示[16]：

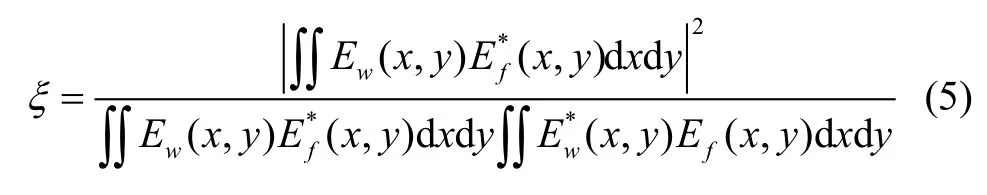
式中Ew表示波导模场，Ef表示光纤模场。对于均匀单模光纤（SMF）而言，其基模光场在光纤横截面上呈现为类高斯分布，如图3(a)所示。而APE-LN波导的折射率分布并不对称，其OXZ波导折射率分布截面如图3(b)所示。其中绿色区域为质子交换区域，宽度为w，扩散深度为hx，折射率差Δn为扩散源沿轴向晶体内部扩散得到的表面（最大）折射率增量，n0为铌酸锂衬底的折射率。

图3 波导结构与模场分布Fig.3 Waveguide structures and mode field distributions

对于x切铌酸锂材料，质子交换形成的光波导折射率表达式为：

其中，g(x)为x方向上的折射率分布，f(z)为沿z方向的分布由函数，γ为扩散型折射率的指数幂。x方向上的折射率分布由函数g(x)为高斯型，其表达式为:

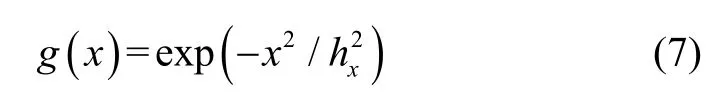
其中，hx为质子源扩散深度的1/e，hz为z方向上的扩散宽度，γ=hz/hx为扩散比。沿z方向的折射率分布函数f(z)为误差函数型，其表达式为：

其中w为z方向上扩散源的宽度。利用基于时域有限差分法的FDTD solutions光学仿真软件可以得到其模场分布，如图3(b)所示，根据仿真结果可知，其基模光场纵向分布不对称，根据上文分析，这将会产生较大的光纤-波导耦合损耗。

针对这一问题，本文提出在APE-LN波导上方覆盖一层LN材料的方法来改善模场分布不对称的方法，如图3(c)所示，利用离子注入和键合技术[14]在APE-LN波导表面覆盖一层LN材料，以此来改变APE-LN波导上表面的折射率分布，使得波导出射的光斑变为对称分布，从而达到减小耦合损耗的目的。导基模模场分布的改善情况，在保证单模传输的前提下，挑选了一组质子交换铌酸锂波导参数（w=6.0 μm,hx=5.5 μm,Δn=0.011），利用FDTD solutions仿真得到了模场纵向分布的变化情况。图4(a)展示了在1550 nm处，APE-LN的基模模场分布，沿图中红色箭头所示方向考察其截面，则可得到如图4(b)所示的模场纵向分布曲线，可以清晰地看到其呈现非对称形状，在图中y＜ 0 μm的方向上，呈指数型衰减，在y= 0 μm处模场分布戛然而止。作为对比，图4(c)(d)则展示了在上表面覆盖LN材料后，模场纵向分布在y= 0 μm两侧呈现对称分布，初步印证本方法可行性。

图4 APE-LN波导模场分布变化情况Fig.4 Mode field distribution of APE-LN waveguide mode为更加直观地考察覆盖LN层前后，APE-LN波

2.2 空芯光子晶体光纤的建模

如上文所述，该谐振腔的构建需要信号光从波导有效耦合到实芯光纤和空芯光子晶体光纤中，因此建立实芯光纤与空芯光子晶体光纤的模型，对理论仿真至关重要。对于实芯光纤的模型采用常见的SMF-28光纤，其基模模场分布如图3(a)所示，由于其建模方法已经非常成熟，这里就不再赘述。接下来，主要进行空芯光子晶体光纤的建模仿真。在FDTD solutions中建立空芯光子晶体光纤的二维横截面结构模型，对标物为图5(a)所示的NKT公司的商用7芯光子晶体光纤NKT-1550-02。

图5 空芯光子晶体光纤的设计Fig.5 Design of the HCPCF

经过多轮优化仿真，综合对光子带隙光纤的光子带隙设计、损耗特性研究，最终确定了光纤结构的参数设计结果，如图5(b)所示，其中R= 1 μm，T= 100 nm分别代表毛细管的内切圆半径和两毛细管间壁面厚度，r= 0.35 μm，t= 30 nm分别代表五边形底边的内切圆半径和壁面厚度，Λ= 3.8 μm代表毛细管周期间距，d= 3.84 μm代表毛细管内径，Rc= 5.71 μm代表纤芯半径。设定参数后求解，在波长为1550 nm的情况下，得到如图5(c)所示的纤芯基模模场分布。最终选择该光斑作为目标光斑。

2.3 耦合效率仿真计算

将仿真得到的HCPCF模场分布与SMF光纤模场分布导入FDTD solutions中，与覆盖LN上包层的APE-LN波导进行耦合效率仿真计算。为了模拟APE-LN波导上包层为LN材料，设置整个求解空间的背景材料为LN。

通过计算波导出射光斑与光纤光斑的重叠积分，可以得到在不考虑菲涅尔反射情况下的耦合效率。经过多轮参数优化，最终得到APE-LN波导在线宽w=7.0 μm，扩散深度hx=6.0 μm情况下，其出射光斑与光纤光斑耦合效率最高。图6(a)展示了APE-LN波导在w=7.0 μm，hx=6.0 μm时，与HCPCF的耦合效率随Δn的变化情况，其中虚线表示APE-LN波导在没有覆盖LN包层时耦合效率的变化趋势。可以看出，随着Δn的不断增大，可以将APE-LN波导与HCPCF的耦合效率从0.8239提升到0.8937，在Δn= 0.014时达到最大，然后开始减小。实线表示覆盖LN上包层后APE-LN波导与HCPCF的耦合效率变化趋势，其变化也是随着Δn的增大，先增大后减小，在Δn= 0.016时达到最大为0.9114。通过对比两条曲线，可以明显看出，覆盖上包层的APE-LN波导与HCPCF耦合效率普遍更高，再次印证了覆盖LN材料对APE-LN出射光斑的改善作用。

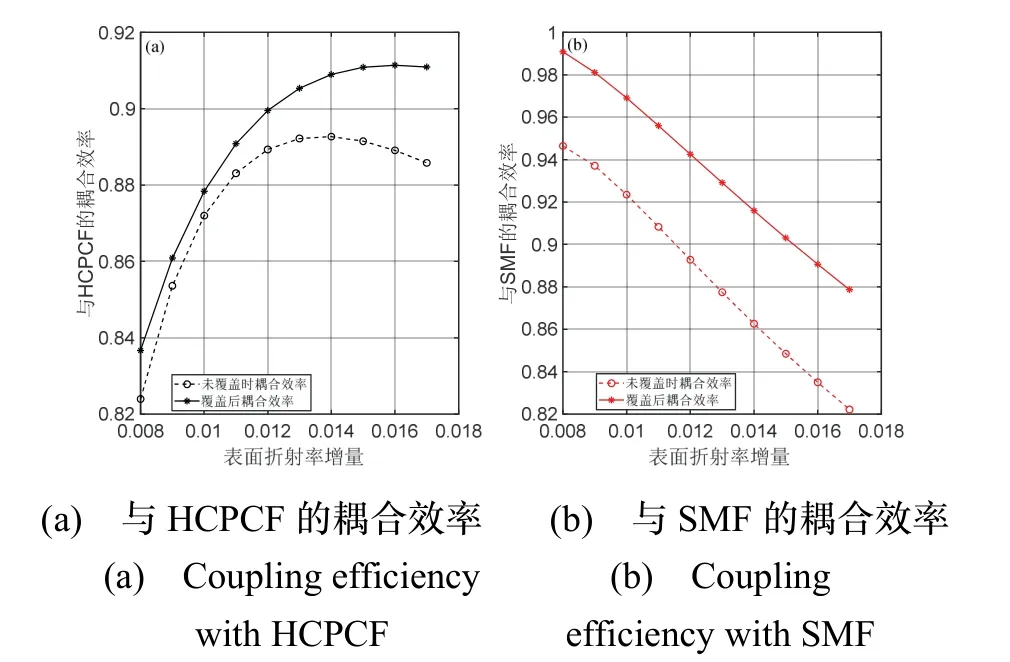
图6 APE-LN波导与光纤耦合效率的仿真优化Fig.6 Simulation optimization of the coupling efficiency between APE-LN waveguide and fiber

图6(b)展示了APE-LN波导在w= 7.0 μm，hx= 6.0 μm时，与SMF的耦合效率随Δn的变化情况。首先，通过覆盖LN上包层前后的曲线对比，可以看出，覆盖上包层后APE-LN波导相比于未覆盖的APE-LN波导而言，与SMF耦合效率更高，表明覆盖LN上包层对APE-LN波导与普通单模光纤的耦合效率也有提升作用。其次，可以看出，随着Δn的增大，APE-LN波导与SMF的耦合效率不断降低，与图6(a)的变化趋势刚好相反。这表明在选择波导参数时，需要在两个耦合损耗之间寻求平衡。根据上文分析结果，HCPCF与波导的耦合损耗对谐振腔性能影响更大，因此优先考虑提高与HCPCF的耦合效率，同时兼顾与SMF的耦合损耗。最终选择参数为w= 7.0 μm，hx= 6.0 μm，Δn= 0.015，此时，与HCPCF的耦合效率为0.9109，与SMF的耦合效率为0.9031。

由于实际的LN上包层覆盖的厚度是有限的，不会如上文仿真设置的无穷大厚度，因此需要考虑在加工时，覆盖的LN层厚度变化对APE-LN的出射光斑改善的影响，从而寻求一个最合适的覆盖厚度。在上文参数给定的情况下，最终的仿真结果如图7所示，随着覆盖LN层厚度的增大，APE-LN波导与两种光纤的耦合效率均是先增大后趋于平缓。其中与HCPCF的耦合效率在覆盖厚度为3 μm时达到最大为0.9152，较之前理想化的仿真结果0.9109有所提升，而后随着覆盖厚度的增加而减小，最终保持不变。该结果表明实际加工中可以通过调整工艺参数进一步提升与HCPCF的耦合效率。与SMF光斑的耦合效率在覆盖厚度为12 μm时达到最大为0.9031，此后趋于不变。根据以上仿真结果，本文选定上包层的覆盖厚度为3 μm，此时，与HCPCF的耦合效率为0.9152，与SMF的耦合效率为0.8847。

图7 覆盖LN层厚度不同导致的耦合效率变化Fig.7 The relationship between the coupling efficiency and thickness of the LN cladding

由于键合技术对材料的表面平整度有要求，所以在实际加工时，需要先对APE-LN上表面进行化学机械抛光，而后将上包层LN材料与下方APE-LN材料相对粘合，通过退火使其牢牢粘住。为分析抛光时磨去的APE-LN上表面厚度对最终耦合效率的影响，本文进行了仿真分析。分析结果如图8所示，磨去厚度在0到500 nm不断增加时，覆盖3 μm LN层的APE-LN波导与HCPCF的耦合效率随之不断减小；相反的，与SMF的耦合效率却随之不断增加。因此，在实际加工时应尽量减小APE-LN上表面被磨去的厚度，以保证腔内耦合损耗最低。若选择磨去厚度为100 nm，则最终得到实际加工出来的覆盖上包层APE-LN波导与HCPCF耦合效率为0.9147（耦合损耗约0.39 dB），与SMF的耦合效率为0.8852（耦合损耗约0.53 dB）。

图8 磨去波导上表面的厚度对耦合效率的影响Fig.8 Influence of the thickness of the polished waveguide upper surface on the coupling efficiency

2.4 谐振腔性能分析

根据仿真得到的耦合损耗：αs=0.53 dB，αp= 0.39 dB，并结合RFOG的理论极限灵敏度表达式(3)与第2节中谐振腔的其他参数，可以得出该条件下陀螺的极限灵敏度为0.114 °/h，达到了战术级应用要求。且该方案谐振腔由APE-LN波导和HCPCF构成，具有小体积，抑制偏振波动、光克尔噪声等优势，有一定的应用前景。

3 结 论

本文提出，通过端面对准耦合的方式，可以将HCPCF环与APE-LN波导耦合器进行有效连接，从而构成一种具有单偏振低噪声特性的HCPCF谐振腔。针对传统APE-LN波导与光纤对准耦合损耗较大的问题，提出了使用离子注入和键合技术在波导上表面覆盖一层LN材料作为上包层，从而对APE-LN波导模场分布进行改善，利用时域有限差分数值分析方法建立波导和光纤的模型，根据模场匹配模型对耦合效率进行了仿真分析，探讨了波导结构、工艺参数的影响，经过优化设计，可以将HCPCF与波导的耦合损耗减小至0.39 dB，陀螺精度提升至0.114 °/h。本文对HC-RFOG的谐振腔设计有一定的参考意义。下一步可以通过继续优化空芯光子晶体光纤的模型，构建与实际空芯光纤模场更加接近的目标光斑，从而提高仿真的准确性。此外，继续对APE-LN波导进行优化设计与模斑改善，不断降低光纤与波导的端面对准耦合损耗，不断提高该方案谐振腔的性能，为构建单偏振、低噪声、易装配、小体积的高性能谐振式空芯光子晶体光纤陀螺打下坚实基础。