考虑地球扁率误差的两步Kalman滤波星光导航方法

2022-01-15林宝军刘迎春武国强

中国惯性技术学报 2021年5期

林夏，林宝军，刘迎春，白涛，武国强

（1. 上海微小卫星工程中心，上海 201210；2. 中国科学院空天信息创新研究院，北京 100094；3. 中国科学院大学，北京 100094； 4. 中国科学院微小卫星创新研究院，上海 201210；5. 上海科技大学，上海 201210；）

天文导航是一类重要的卫星自主导航方法。通过对天文信息的连续观测，卫星可实现自身位置、速度等导航信息的自主确定[1,2]。利用星敏感器与地球敏感器观测信息的星光导航是其中一种适用于地球卫星的天文导航方法。星光导航法实现方法简单，稳定可靠，在低、中、高轨卫星中都有着较多的应用[3]。

但由于地球敏感器敏感地平时存在较大误差，因而相比于其他的自主导航方法，星光导航法精度较低，在使用上也受到了许多限制[4]。地球敏感器敏感地平误差由季节变化、地球扁率、环境温度、安装偏差、随机噪声等多种因素引起[5]。而在这些误差源中，地球扁率造成的影响最为显著。学者Tekawy[6]、Li Jie[7]、杨博[8]等人均针对地球扁率误差提出了相应的修正方法，但这些算法均需要已知卫星轨道信息，并不适合在自主导航算法中直接使用。文献[9]提出了一种不基于轨道先验信息的地球扁率误差修正方法，但算法基于双圆锥扫描地球敏感器模型设计，并不适合在其他类型的地球敏感器中应用。

为实现地球扁率误差的星上自主修正，从而提高基于星敏感器与地球敏感器观测信息的星光导航算法精度，本文提出了一种基于两步Kalman滤波的星光导航实现方法。首先，基于粗略星光角距观测信息，利用Kalman滤波算法得到含有一定误差的卫星粗轨道信息；而后，利用粗轨道信息计算地球敏感器的地球扁率误差以实现误差自主补偿，得到精度较高的星光角距观测信息；最后，基于修正后的星光观测信息，再次利用Kalman滤波算法对卫星轨道信息进行估计，获得精度较高的卫星自主导航信息。

本文首先介绍了星光导航算法的原理，并依据地球敏感器敏感地平原理研究了地球扁率误差的自主修正方法，而后详细给出了两步Kalman滤波星光导航算法的设计方法，最后通过仿真验证了算法的有效性。

1 星光导航算法原理

星光导航算法利用星敏感器与地球敏感器对卫星星光角距信息进行测量，并应用Kalman滤波算法对卫星动力学方程获得的一步轨道信息进行修正，最终得到卫星导航信息的最优输出。本节将从卫星动力学模型，算法观测模型与算法滤波模型三方面对星光导航算法进行详述。

1.1 卫星动力学模型

依据牛顿定律，卫星动力学方程可表示为：

式中，r、v分别为卫星的位置、速度向量。a为卫星加速度向量，可由式(2)表示。wr、wv为位置速度向量的过程噪声信息，可视为白噪声向量。

式中，μ=Gm为地球引力常数，G为万有引力常数，m为地球质量。aNS为地球非球形引力，aNB为N体摄动力加速度，主要为日月引力加速度，aSRP为卫星光压摄动力加速度，aDG为大气阻力加速度。

1.2 观测模型

星光导航算法一般通过观测星光角距信息进行自主导航，观测模型如图1所示，具体模型构造方法描述如下。

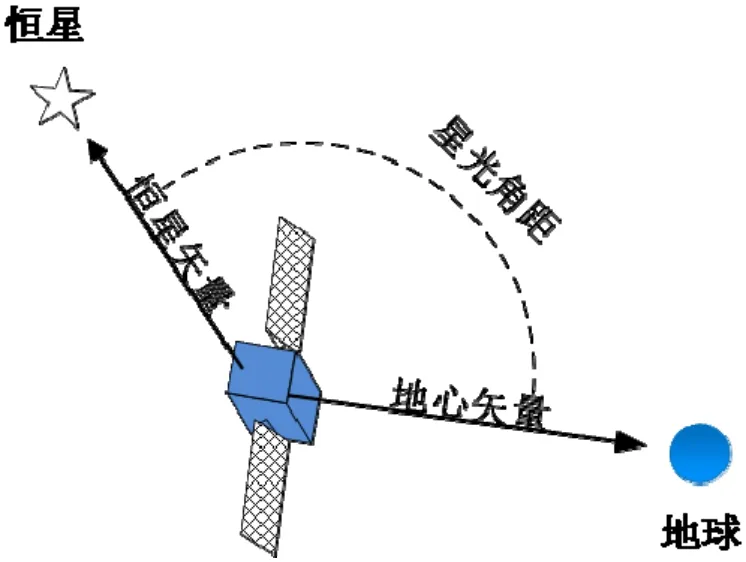
图1 星光角距观测模型示意图Fig.1 Observation model of starlight angle

首先，卫星可利用星敏感器观测得到在星敏感器坐标系下的单位恒星矢量结合星敏感器安装矩阵Rbs及式(3)，可得到卫星本体坐标系下单位恒星矢量表示。

并且，卫星可利用地球敏感器观测得到地球敏感器坐标系下的单位地心矢量表示，结合地球敏感器安装矩阵Rbe及式(4)，可得到地心指向在卫星本体坐标系下单位地心矢量表示。

同时，为对卫星导航信息进行修正，建立卫星位置信息r与星光角距信息θ的关系，形成观测方程如下：

1.3 滤波模型

由于无迹卡尔曼滤波（UKF）[10]算法不需对{ 非线性系统做简化近似，相比于扩展卡尔曼滤波算法（EKF），无迹卡尔曼滤波（UKF）算法对于非线性系统有更好的表现。因此对于滤波模型的处理，本文采用UKF算法。

2 基于星光导航的地球扁率误差自主修正

2.1 地球敏感器敏感地平原理

以圆锥扫描地球敏感器为例，地球敏感器通过扫描地球采集扫入地球点Pin与扫出地球点Pout，确定敏感器坐标系下地心矢量指向。地球敏感器敏感地平模型如图2所示，具体求解方法如下所述。

图2 地球敏感器敏感地平模型图Fig.2 Scanning model of the horizon sensor

地球敏感器绕扫描轴匀速转动，当捕获地球时，可获得扫入地球时间tin，扫出地球时间tout。通过与扫过基准点时间tr相减，可获得地球敏感器敏感地平的扫描相角Uin、Uout，具体计算方法如式(8)所示[11]。

式中，Ts为地球敏感器的扫描周期。

假设地球敏感器扫描圆锥轴心沿卫星本体系+Y方向，且地球敏感器敏感姿态角—俯仰角与滚动角较小，那么卫星的俯仰角∂与滚动角φ可通过式(9)计算得到。相应地，地心矢量在敏感器坐标系下的表示可由式(10)计算得到[12]。

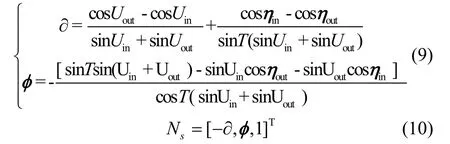
式中，ηin和ηout分别为地球敏感器扫入点天底角与扫出点天底角，T为地球敏感器的半锥角。

2.2 地球扁率误差自主修正方法设计

由式(9)(10)可知，地球敏感器敏感地平精度由扫描相角Uin、Uout，敏感器半锥角T及天底角ηin、ηout精度确定。由于扫描相角及半锥角均可精确测量，因而地球敏感器敏感地平精度取决于天底角精度。地球扁率误差为影响天底角精度的主要因素。由于地球扁率误差修正需已知卫星位置信息，本节设计了基于星光导航信息的地球扁率误差自主修正方法。

地球为一个南北方向较扁的椭球，在零经度辅助惯性坐标系下的地球球面方程如式(11)所示。

式中，e为地球扁率系数，Re为赤道半径。

显然，由于地球的扁球特性，地球敏感器扫入扫出点距地球中心的地心距并非为标准的地球赤道半径Re，因而当利用式(12)计算天底角时，计算结果将不可避免地存在一定偏差。

基于此，本节设计的地球扁率自主修正方法如下：

首先，采用天文导航算法得到连续稳定的卫星位置信息，该信息引入式(13)中，可计算出地球敏感器穿越点坐标。式(13)可利用地球敏感器敏感地平模型得出，一般采用牛顿迭代法对式(13)求解[6]。

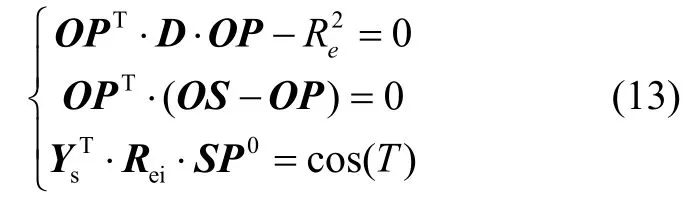
式中，P为地球敏感器扫入扫出地平的位置信息，S为卫星位置，O为地心原点。因而，OP为穿越点惯性坐标系位置向量，OS为卫星地心矢量，0SP为卫星到穿越点的惯性坐标系下的单位向量表示。同时，D=diag(1,1,1/(1 -e)2)，Ys为地球敏感器扫描轴在敏感器坐标系的单位向量表示，Rei为惯性坐标系到地球敏感器坐标系转换矩阵，可通过式(14)计算得到。式(13)中所有符号也均在图2中加以标注。

式中，Rsi为惯性坐标系到星敏坐标系的转换矩阵，其可通过星敏感器实时输出惯性系四元数信息转换得到。

3 两步Kalman滤波星光导航算法设计

基于上节所述地球扁率误差自主修正方法，本节设计了两步Kalman滤波算法以将地球扁率误差修正算法嵌入星光导航算法中，从而实现地球扁率误差的自主修正及星光导航算法精度的提升。两步Kalman滤波星光导航算法设计如图3所示。首先，算法利用地球敏感器原始输出的地心矢量信息与星敏感器输出的星光指向信息形成粗星光角距信息。将粗星光角距信息与所需轨道位置速度、协方差预报信息引入星光导航滤波器中得到存在一定误差的卫星粗位置信息。算法将卫星粗位置信息引入2.2节描述的地球扁率误差修正方法中，修正地球敏感器输出，从而获得精确的地心矢量信息。而后，将得到的精地心矢量信息结合星敏感器输出获得精确的星光角距观测信息，并将精星光角距信息再次代入星光导航算法滤波器中对卫星轨道信息进行滤波求解，最终可得到精确的卫星轨道信息及相应的协方差信息的更新输出。

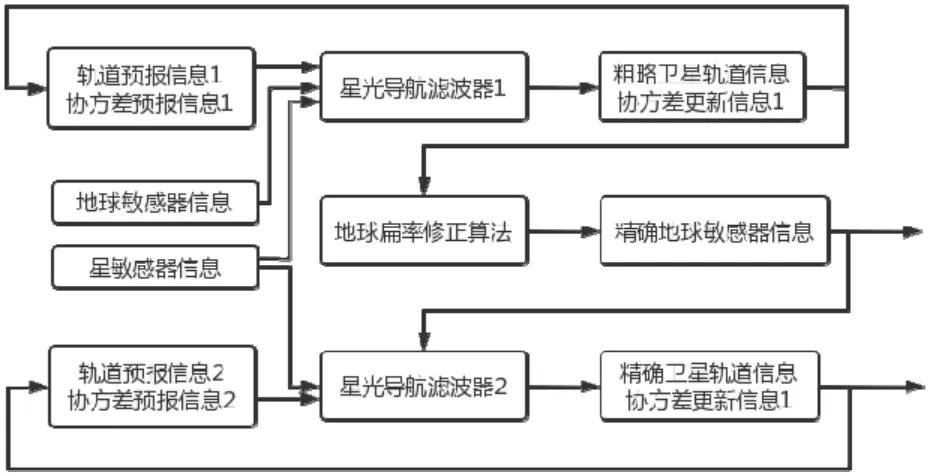
图3 两步Kalman滤波星光导航算法设计图Fig.3 Design of the starlight navigation algorithm based on the two-step Kalman filter

4 仿真分析

本节对设计的两步Kalman滤波星光导航算法进行仿真分析，通过与传统的星光导航算法比较，评估设计算法的自主导航精度以及地球扁率误差修正效果。

4.1 仿真场景建立

仿真中选用的卫星轨道为一LEO卫星轨道，轨道参数及敏感器参数设置如表1所示。

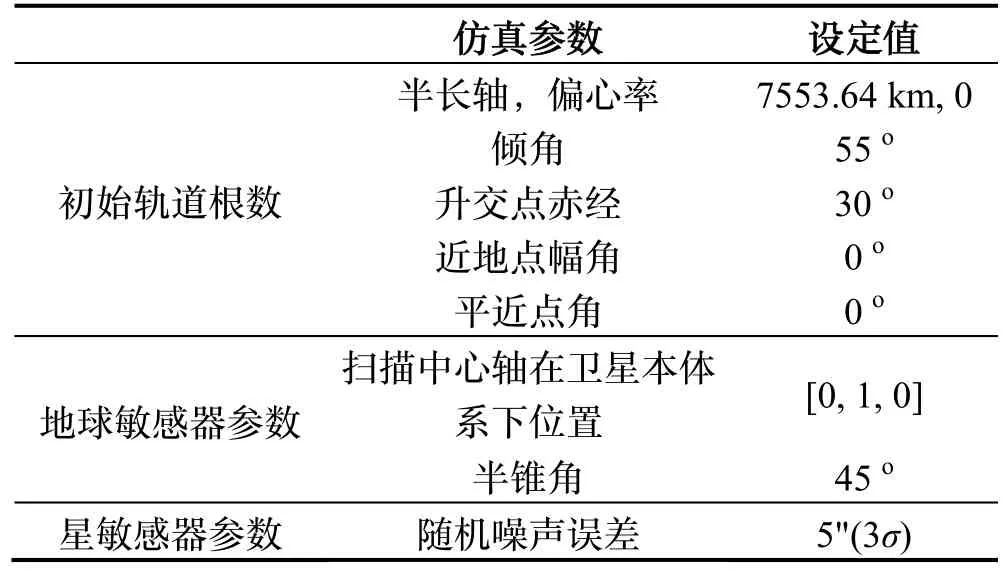
表1 算法仿真参数Tab.1 Simulation parameters

同时，卫星采用偏航机动模式调整姿态，即其+Z轴指向地心，并且太阳矢量一直保持在卫星本体系+XOZ面内。仿真采样周期设定为4 s，仿真时长为43200 s。

4.2 仿真结果分析

首先对地球扁率引起的地球敏感器敏感地平误差进行评估。如图4所示，仿真得到的地球敏感器测量的俯仰角与滚动角最大误差分别为0.327 °和0.116 °。根据地球敏感器俯仰角、滚动角与单位地心矢量的关系，可相应计算得到由地球扁率引起的单位地心矢量误差。

图4 地球敏感器滚动俯仰误差图Fig.4 Roll and pitch errors in the horizon sensor

而后利用仿真得到的单位地心矢量信息，可应用星光导航算法，对传统星光导航算法的性能进行评估。以精确的轨道外推模型为基准，可精确确定传统的星光导航算法误差。如图5所示，三轴位置误差分别为26045 m，32553 m，22852 m；三轴速度误差分别为21.930 m/s，20.475 m/s，24.811 m/s。可以看到，地球扁率误差严重影响了星光导航算法的自主导航精度。

图5 传统星光导航算法位置误差图Fig.5 Position errors in the traditional celestial navigation method

随后，应用本文设计的两步Kalman滤波星光导航算法，对敏感器地球扁率误差自主修正精度及星光导航算法精度进行评估。图6、图7分别为经两步Kalman滤波算法计算后的修正后地心矢量误差及星光导航算法误差。如图6所示，经两步Kalman滤波算法，修正后的地球敏感器滚动角及俯仰角最大误差分别为0.0011o、0.0006o，地心矢量指向被精确确定。同时，利用修正后的单位地心矢量，可得到精确的星光角距观测信息，因而星光导航算法精度也得到极大提升。如图7所示，待算法收敛后，三轴最大位置误差分别为1508.2 m，947.0 m，2836.8 m；三轴最大速度误差分别为3.721 m/s，3.540 m/s，4.146 m/s。

图6 传统星光导航算法速度误差图Fig.6 Velocity errors in the traditional celestial navigation method

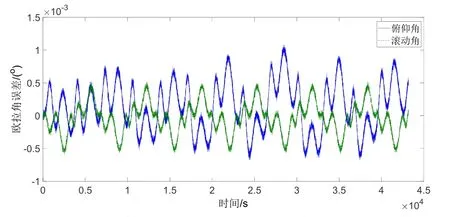
图7 修正后地球敏感器滚动俯仰误差图Fig.7 Roll and pitch error in the horizon sensor after revised

最后，将本文设计的两步Kalman滤波星光导航算法与传统的星光导航算法得到的地心矢量精度及卫星轨道信息精度分别进行比较。表2为两算法比较结果。相比于传统的星光导航算法，利用本文设计的两步Kalman滤波星光导航算法，地心矢量精度及卫星轨道信息精度均提高了80%以上。因而，两步Kalman滤波星光导航算法的有效性得到了有效地验证。