考虑信息滞后的AUV因子图多源信息融合定位算法
2022-01-15黄紫如柴洪洲向民志杜祯强王栋民
黄紫如,柴洪洲,向民志,李 达,杜祯强,王栋民
(1. 信息工程大学 地理空间信息学院,郑州 450001;2. 自然资源部海洋测绘重点实验室,青岛266590;3. 天津航海仪器研究所,天津 300131)
海洋已成为人类可持续发展和资源开发的重要领域[1]。自主水下潜航器作为获取海洋资源和拓展海洋军事领域的重要工具,保证其成功高效运行的关键问题是进行实时精确定位[2]。目前,水下传感器的种类不断增多,最常用的自主水下潜航器(Autonomous underwater vehicle, AUV)定位方式是利用捷联惯导系统(Strapdown Inertial Navigation System, SINS),其状态参数全面,自主性好且隐蔽性高,但定位误差会随着时间积累,需要辅助传感器进行修正。水下声学测速与定位技术因其传输距离远、衰减损失小,在现阶段水下定位中必不可少[3],其中多普勒测速仪(Doppler Velocity Log, DVL)为AUV航行提供速度观测信息,反应敏捷、稳定性好;超短基线(Ultra-Short Base Line, USBL)定位系统使用简易灵活、可移动范围大,精度较高,得到了广泛应用。但声学数据传输速率较低,输出参数连续性较差,为了增强定位系统的可靠性、提高AUV定位精度,需要融合多源信息,实现优势互补、互为余度、协调超越。
在水下组合导航方面,现有研究融合了多种传感器信息进行定位[4-6]。但在复杂环境中,水声传播速度慢, 脉冲串和通信数据包发送、接收与处理时间长,易造成传感器信息延迟到达,对AUV定位的影响不容忽视。针对信息滞后的问题,基于滤波的数据处理方法主要为拟合推估,将滞后数据拟合归算至当前时刻,作为等效观测值参与融合[7],但此类方法会引入推估误差,无法进行高效完整的信息利用;此外,还可以维持用于储存历史状态的滑动窗口,当滞后信息到达时从窗口原点重新解算,可以无损利用时延信息,但计算负载大大增加。
近年,因子图方法逐渐兴起。因子图是一种概率图模型,可以表示随机变量的联合概率分布的全局分解,依照各传感器信息的时间标定义对应时刻的因子节点来扩展因子图,即可实现传感器即插即用。马晓爽等采用因子图算法融合AUV多传感器信息进行定位[8],有效解决了传感器更新频率异步的问题。考虑到因子图的全局解算特性,可以实时追溯历史时刻变量节点,能够高效快速地融合滞后测量信息,高军强等将因子图算法应用于GPS/INS组合导航系统中,降低了GPS信息滞后产生的定位误差[9]。目前尚缺乏利用因子图优化(Factor graph optimization, FGO)算法处理水下传感器延迟信息的研究。
综上,本文提出了一种考虑信息滞后的AUV因子图多源信息融合定位算法,来处理水下传感器延迟信息。研究基于USBL/DVL/SINS融合定位的因子图模型构建及推理方法,提出处理滞后信息的算法策略,并采集水下航行器在海上测试实验数据进行算法验证。
1 基于因子图的多源信息融合方法
1.1 系统模型与算法原理
因子图是用来表达随机变量的联合概率分布的图模型[10,11]。它由因子节点fi、变量节点xi以及边组成,边是指当且仅当因子节点与变量节点相关联时的连接边。在构建多源信息融合定位因子图框架时,首先要将时间序列中的状态变量建模为变量节点:
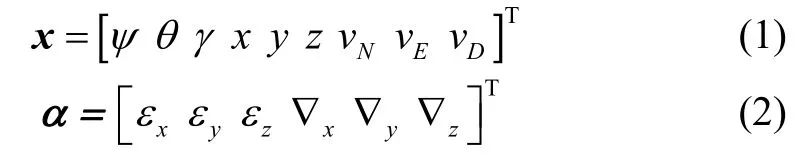
其中,x、y、z分别表示北向、东向、地向载体位置变量;vN、vE、vD分别表示北向、东向、地向速度变量;ψ、θ、γ表示三轴姿态变量;εx、εy、εz表示陀螺仪漂移;∇x、∇y、∇z表示加速度计零偏。
设在ti时刻输出的定位状态量为xi,惯性传感器偏置量为α1,则tk时刻的状态变量节点的集合为:
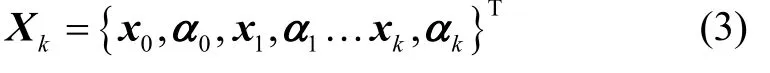
将系统中各传感器在ti时刻的测量值表示为则tk时刻系统接收到的所有测量值的集合为:
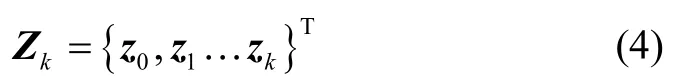
根据贝叶斯估计原理,从t0时刻到tk时刻,时间序列中各个节点状态的联合后验概率密度为:
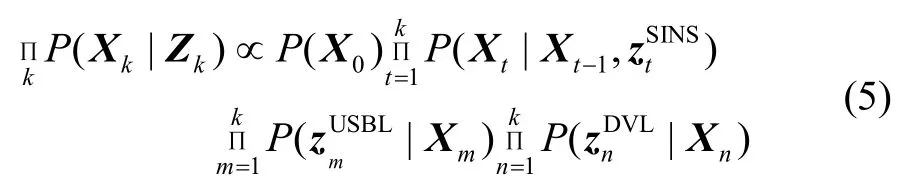
其中,P(X0)表示所有变量的初始状态的先验信息;表示 SINS状态转移模型,分别表示观测更新模型。根据可用观测信息,通过最大后验概率密度(Maximum a Posteriori, MAP)估计获得时间序列中所有状态变量的最优估计:
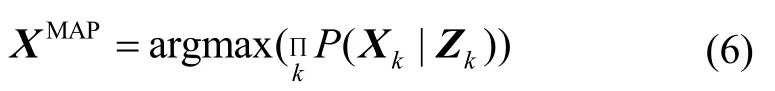
对于服从高斯噪声分布的测量,我们通常将每一个测量模型P(Xk|Zk)定义为一个因子用误差函数来表示,其中表示马氏距离的平方,Σ表示协方差矩阵。于是可以将最优估计问题转化为非线性最小二乘问题:
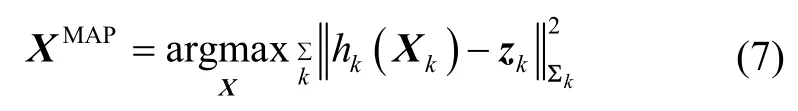
至此,可以利用非线性优化方法对式(7)进行一系列的线性近似,解算得到状态变量的最优估计。
1.2 因子节点模型
由上节可知,构建多源信息融合因子图框架还需要将各个传感器观测信息建模为因子节点。下面分别讨论AUV多源信息融合定位中所用传感器因子模型。
1.2.1 DVL因子节点
基于多普勒效应原理,DVL利用载体移动时发射频率和反射频率的不一致性以及其差值与相对速度呈现线性关系的特点,可以长航时提供精确的对地速度测量信息,且信息的时间延迟很小,可以忽略处理。
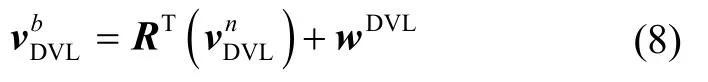
SINS所估计出载体坐标系下速度如下:

AUV速度误差和姿态误差可以表示为:
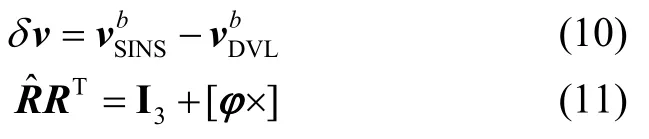
将式(10)(11)代入式(8)可得:
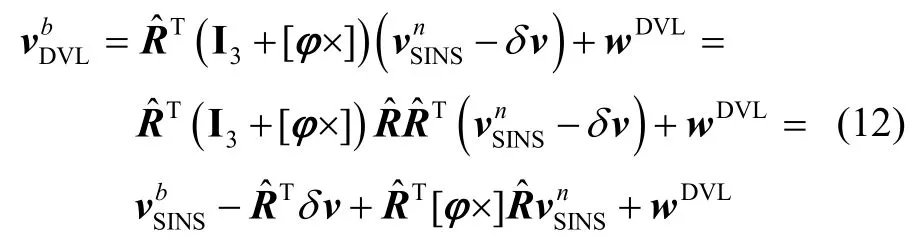
取其差值作为观测误差,观测方程如下:
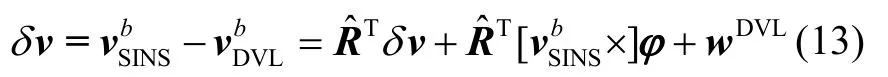
为方便描述,设在tk时刻接收到DVL的速度信息时添加 DVL因子,观测方程为:
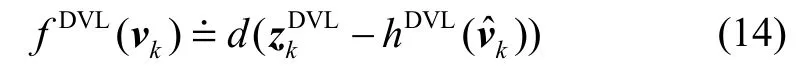
线性化目标函数中的雅可比矩阵HDVL为:
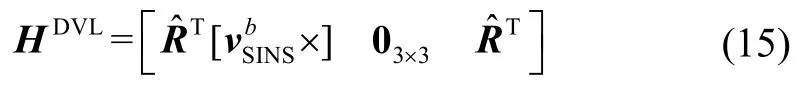
1.2.2 USBL因子节点
使用USBL传感器进行定位时,将基阵安装在AUV上,应答器安装在无人水面载体(Unmanned Surface Vehicle, USV)上,USV浮于水面,此时GNSS观测条件良好,USV可以获得高精度位置信息。AUV利用基阵发射脉冲到应答器的往返传播时间与相位差计算斜距与方位角,从而计算出应答器相对基阵坐标系的三维相对位置,以此构建观测方程对AUV自身位置进行修正[4,12]。
忽略USBL坐标系与载体坐标系间的误差,设s与p分别为导航坐标系下USV上应答器与AUV上基阵的位置矢量。其中s为己知位置矢量,设r为应答器在载体系下的位置矢量,载体系到导航系的变换矩阵用表示,nUSBL代表USBL系统的位置测量噪声。可得AUV的位置观测方程为:
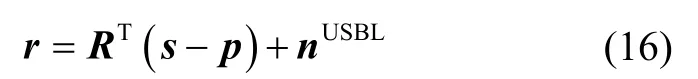
SINS递推得到的载体系下应答器的位置矢量为:

AUV位置误差和姿态误差可以表示为:

将式(11)与式(18)代入式(16)可得:
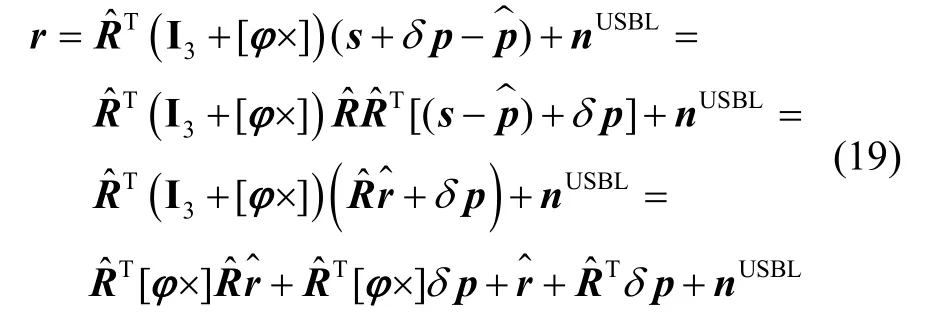
忽略二阶小量的影响,USBL与SINS位置矢量测量值误差方程可以表示为:
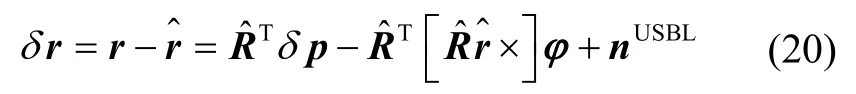
当tk时刻接收到USBL的位置信息,观测方程可列为其误差函数可表示为:
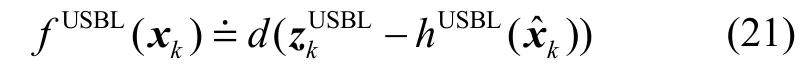
线性化目标函数中的雅可比矩阵HUSBL为:
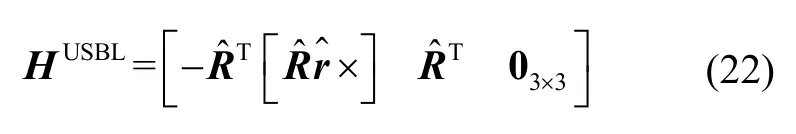
1.2.3 SINS因子节点
因子图算法中通常使用预积分技术将一段时间内的SINS测量值进行积分后转化为一个因子,以指定的频率添加,可以提高计算效率。

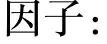
1.3 图模型递推方法
当接收到各传感器的测量信息时,定义因子节点并更新因子图框架,进行变量节点更新。AUV多源信息融合定位因子图框架如图1所示,各个时刻的USBL因子与DVL因子通过连接边与对应状态变量相关联,SINS因子连接了前后相邻的状态变量,为与程序框架相匹配,将Bias因子单独列出[13]。图中虚线部分表示tk时刻新添加到图中的边与状态变量:
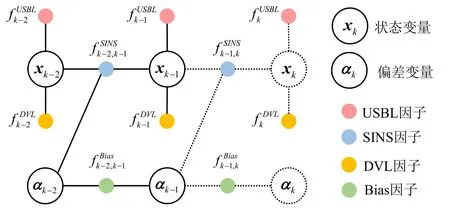
图1 多源信息融合定位因子图框架Fig.1 Multi-source information fusion location factor graph framework
考虑到解算过程中的效率,若在每次接收到新的测量时执行全体状态变量的重新优化,会产生计算负载大,无法实现实时解算的问题。实际上,在图中添加一个新的因子相当于在整体雅可比矩阵中添加一个新行,因此在优化时只有部分变量被更新。基于GTSAM开源库的iSAM2增量平滑技术[14]利用了此特点,每次更新只优化状态变量中受到新因子影响的部分节点,在保留历史变量节点、可以实时添加因子的前提下,实现了更快的解算速度,为灵活处理时延的传感器信息创造了条件。
2 传感器滞后信息处理策略
2.1 信息滞后模型
在实际应用场景中,按照应答器的返回信息是否能够以AUV上的基阵向应答器发射脉冲询问信号的时间顺序依次到达定位系统,可将信息滞后分为信息顺序到达和信息出序到达两种类型[15]。
信息顺序到达如图2所示,应答器发送的通信数据包按照脉冲串播发的前后顺序到达AUV。USBL发送脉冲串后,虽然tk+1时刻的返回信号在tk+δ时刻才到达AUV的滤波器,但早于下一次发送的数据包到达,即为测量信息有延迟但没有出序。
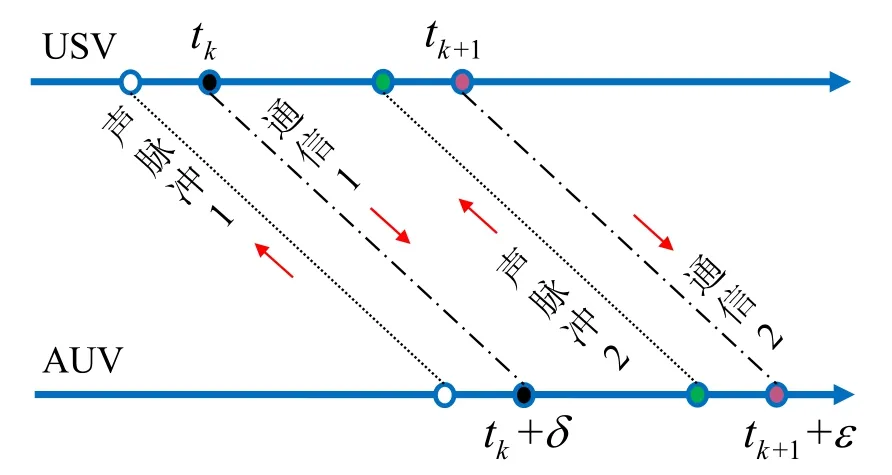
图2 顺序滞后信息Fig.2 Sequential lagging information
信息出序到达如图3所示,应答器发送的通信数据包未按照顺序到达AUV。应答器在tk和tk+1时刻发送的返回信号于tk+δ和tk+1+ε时刻到达AUV,tk+δ时刻晚于tk+1+ε时刻,即为测量信息出序到达。
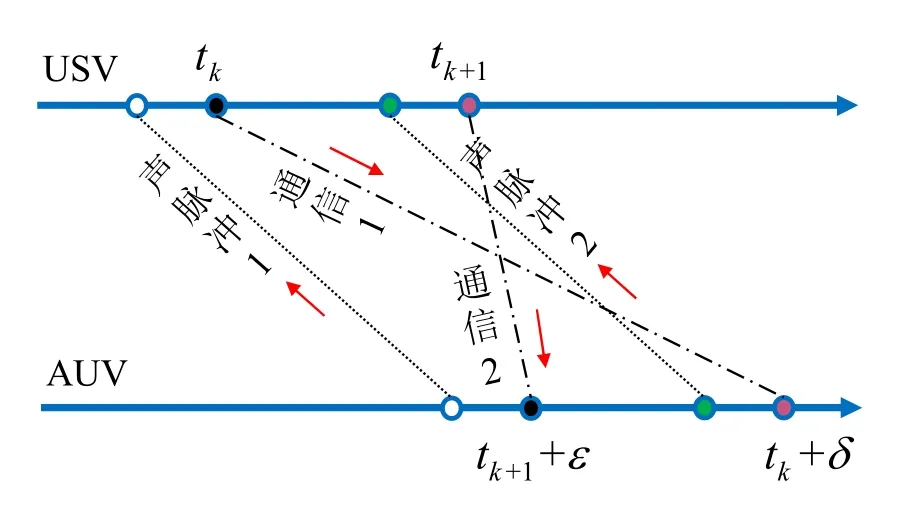
图3 出序滞后信息Fig.3 Out-of-sequence lagging information
2.2 算法流程
由上节已知,因子图算法能够在一个信息融合时刻处理各信息源不同时刻的测量信息[6],具有便捷地融合滞后信息的能力。此外,不同于扩展卡尔曼滤波对于顺序与出序情况需要分别采用不同的模型,因子图方法能够灵活处理两种类型滞后信息。
利用因子图算法处理滞后信息的步骤如图4所示,当接收到传感器数据时,判断其是否有效,若无效则予以剔除;信息正常到达时,在因子图框架中添加对应因子节点与变量节点进行解算;若判断信息存在时延,则匹配到历史时刻的变量节点,在该时刻变量节点上添加因子节点进行重新解算。
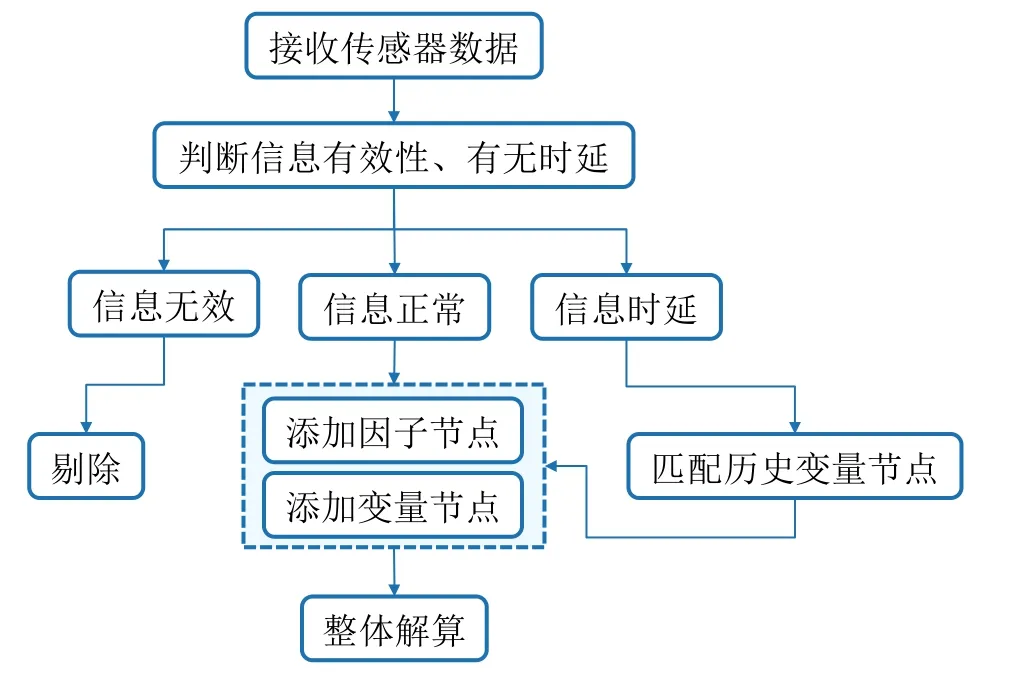
图4 因子图信息滞后算法处理流程Fig.4 The steps of processing lagging information by factor graph algorithm
设USBL测量信息未及时到达,滞后时间为1个历元,即本应该在tk1-时刻到达的信息在tk时刻才被接收。接收到滞后信息的图模型如图5所示,虚线部分表示在接收滞后信息时图模型增添的节点和连接边。
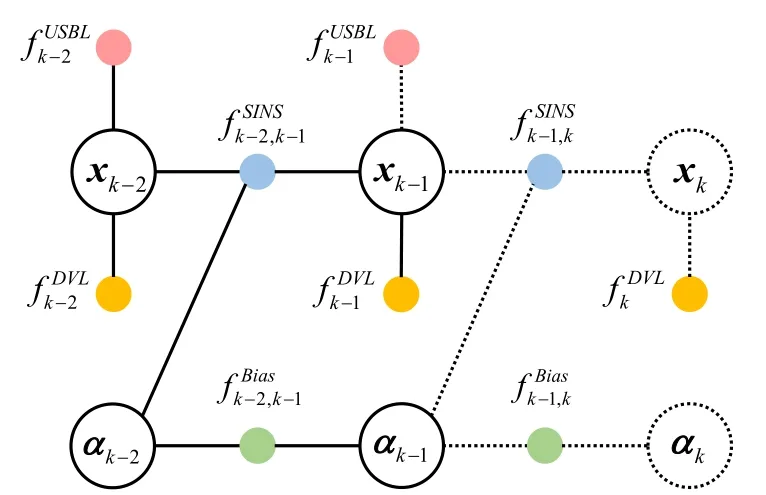
图5 存在信息滞后情况的因子图框架Fig.5 Factor graph framework with information lag

3 半实物仿真试验结果与性能分析
3.1 半实物仿真条件设置
在天津塘沽海面实验中,使用了GNSS、SINS、DVL等多种传感器,获取了一艘自主式水下航行器在水面行驶的数据。
为验证本文所提算法在实际应用中的可用性,提取AUV航行期间的SINS与DVL观测数据,所使用设备的标称参数如表1所示。由于缺乏可用的USBL定位数据,本文将GNSS位置观测信息转换到载体系下模拟USBL应答器在基阵坐标系下的位置观测信息,更新频率为1 Hz,设置0.2%斜距的高斯白噪声。
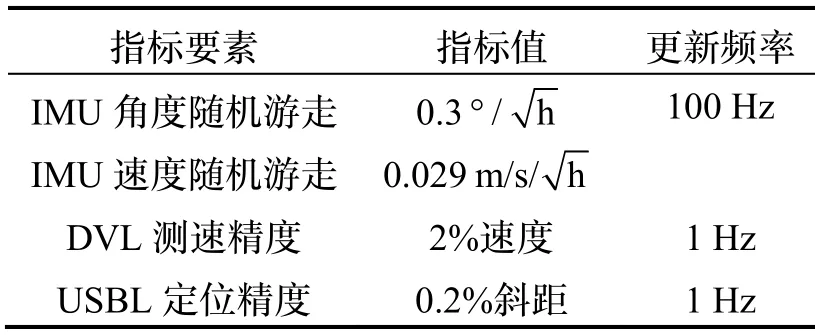
表1 试验设备参数Tab.1 Experimental equipment parameters

图6 实测实验现场Fig.6 The experiment site

图7 AUV轨迹图Fig.7 The AUV trajectory
3.2 试验与分析
在以往的研究中,滤波算法常用曲线拟合法来处理顺序信息,AUV航行速度较慢,因此运动参数在短时间内变化不大,可以用曲线函数来近似描述载体的位置信息并推估当前测量值。对于出序信息,在保证实时性的前提下,可以选择丢弃出序数据[11],简单易行且计算量小,但大量的数据弃用会降低信息利用率,影响定位精度。
为了分析存在因子图信息滞后处理算法的性能,比较在不同USBL信息滞后情况下的效果,本文在海测数据的基础上模拟了顺序、出序以及不同滞后时长下的7组试验进行对比,如表2所示。试验1为传感器信息不存在滞后的情况,可以作为比较基准。
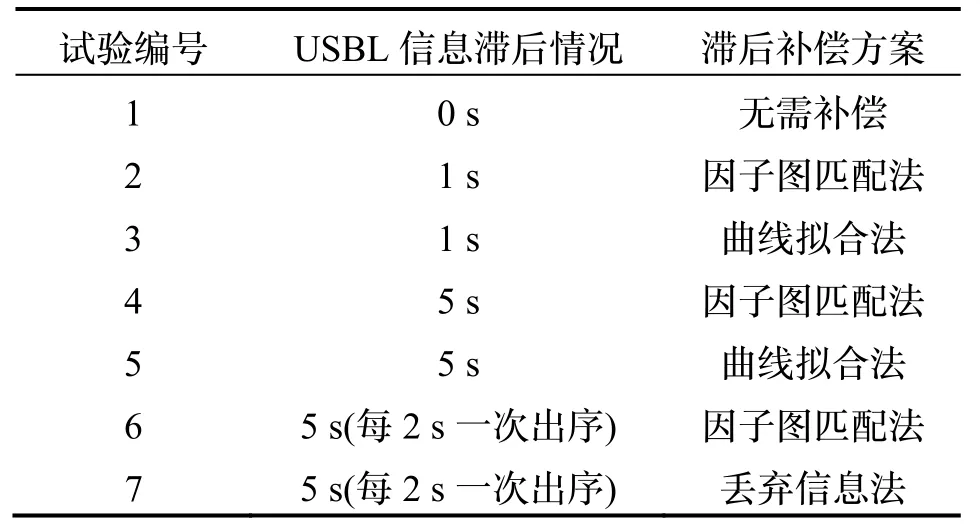
表2 试验条件设置Tab.2 The conditions of each test
首先分析无滞后情况下的USBL/DVL/SINS信息融合算法性能,AUV的高度信息通常由深度计直接提供,因此只需分析平面精度。以GNSS/INS组合导航结果为真值,图8、9分别为位置与速度误差曲线,平面北方向与东方向的位置误差在-2.0~+2.0 m以内,速度误差在-0.5~+0.5 m/s以内。
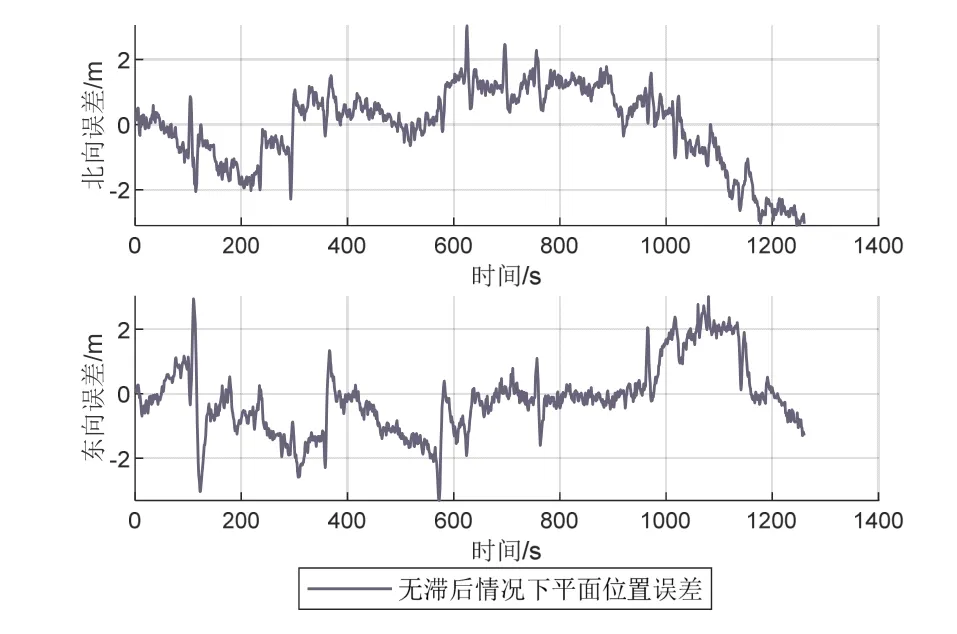
图8 试验1平面位置误差曲线Fig.8 Error curves of plane position in experiment 1
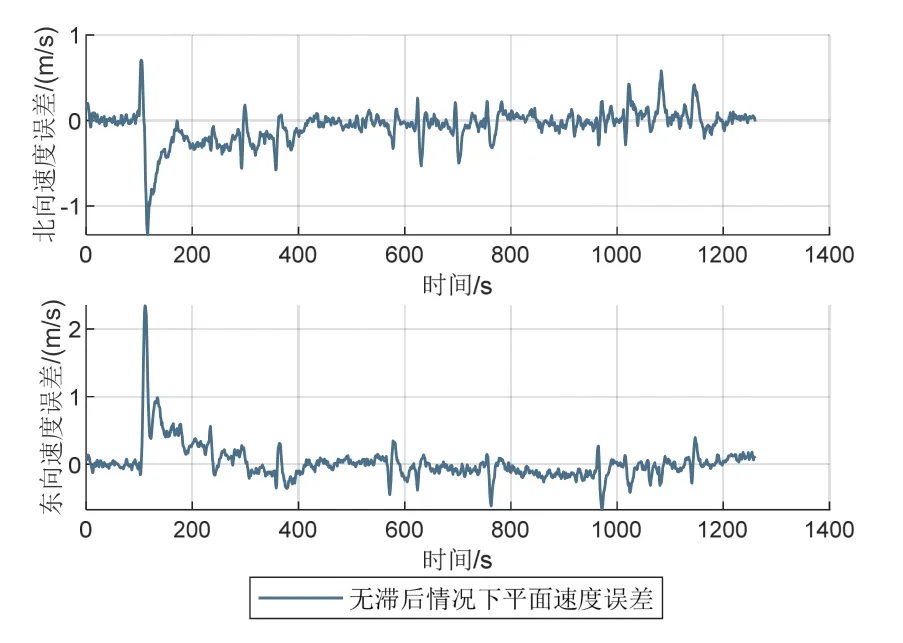
图9 试验1平面速度误差曲线Fig.9 Error curves of plane velocity in experiment 1
为定量分析试验结果,统计实验1、2、3的位置均方根误差(RMSE),如表3所示。图10为试验1、2、3的位置误差曲线对比。显而易见,当USBL信息滞后时间为1 s时,因子图处理方法获得了与理想情况下定位结果相当的定位精度,而曲线拟合法虽然能够保证实时输出定位结果,但精度有所下降。在USBL信息延迟1 s时,相比于曲线拟合法,因子图法解算精度提高了12%。
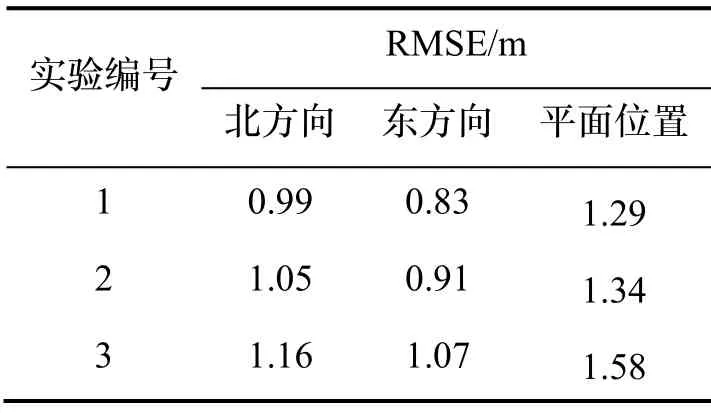
表3 试验1、2、3定位误差统计结果Tab.3 Statistics of position error in experiment 1,2,3
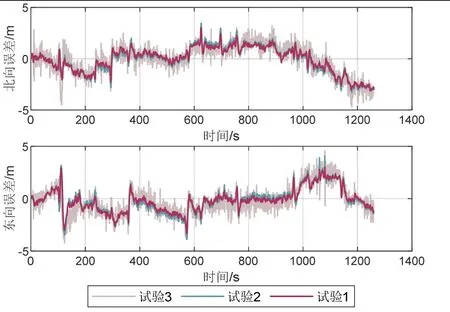
图10 试验1、2、3平面位置误差曲线对比Fig.10 Error curves of position error in experiment 1,2,3
表4为试验1、4、5的位置均方根误差(RMSE),图11为试验1、4、5的位置误差曲线对比。当USBL信息滞后时间为5 s时,由于SINS因子预积分时间间隔增大,误差累积导致因子图方法的定位精度相对于无滞后情况降低41.9%,说明因子图法虽然能够完整利用延迟到达的信息,但无法修正测量信息空白期间的SINS累积的误差。与此同时,同等条件下曲线拟合法向外推断的误差已经达到±10 m,已经无法满足高精度定位需求。综上,相比于曲线拟合法,因子历史信息匹配方法在滞后时间较长情况下更优越,但长时间的误差积累也使其绝对精度下降。
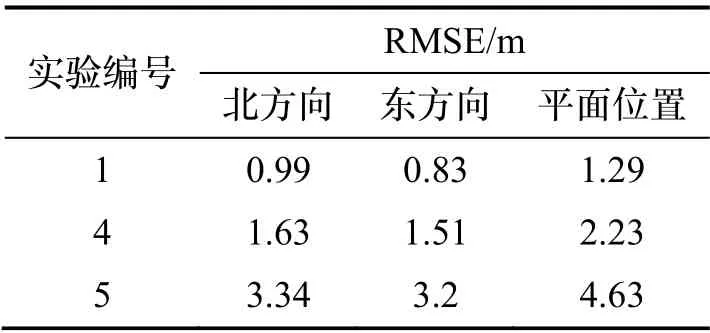
表4 试验1、4、5定位误差统计结果Tab.4 Statistics of position error in experiment 1,4,5
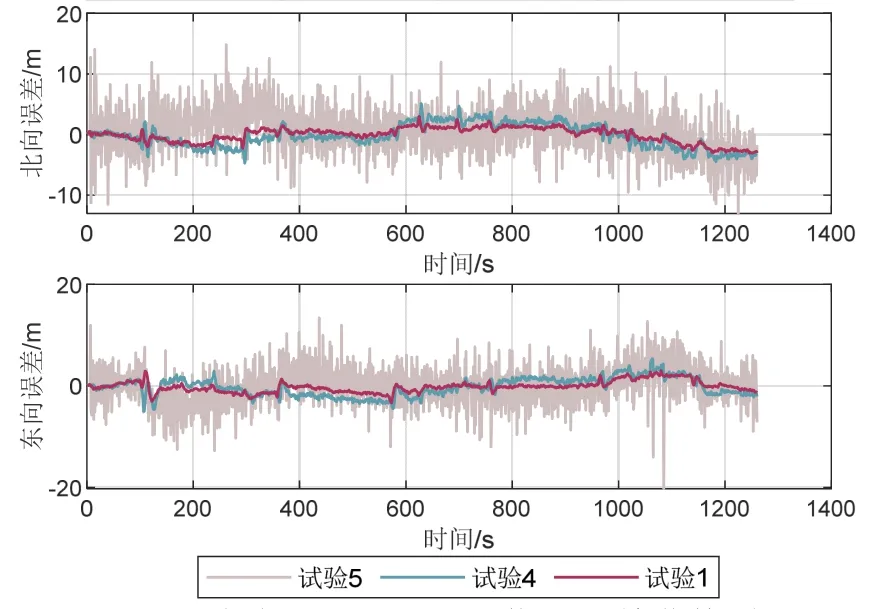
图11 试验1、4、5平面位置误差曲线对比Fig.11 Error curves of position error in experiment 1,4,5
再考察在USBL信息出序的情况下因子图算法的性能。表5为试验1、6、7的平面位置误差统计,位置误差曲线如图12所示。针对信息时延且出序的问题,传统的补偿方法在判断出序信息后通常选择直接丢弃,等待下一个顺序信息到达后再进行更新。与丢弃数据法相比较,因子图匹配法在整体滞后5 s且每2 s发生一次出序的情况下可以提高19.7%的平面精度。因此,使用因子图法能够使出序信息被合理利用,提高信息利用率。
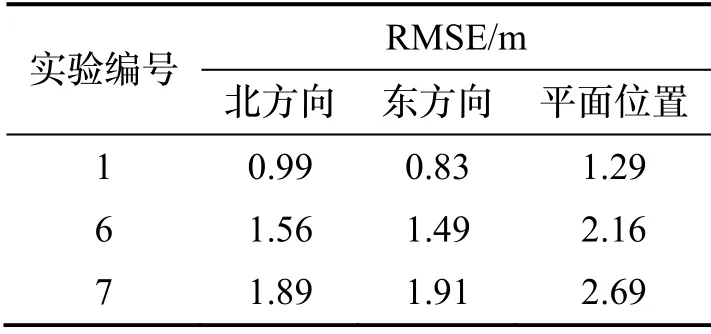
表5 试验1、6、7定位误差统计结果Tab.5 Statistics of position error in experiment 1,6,7
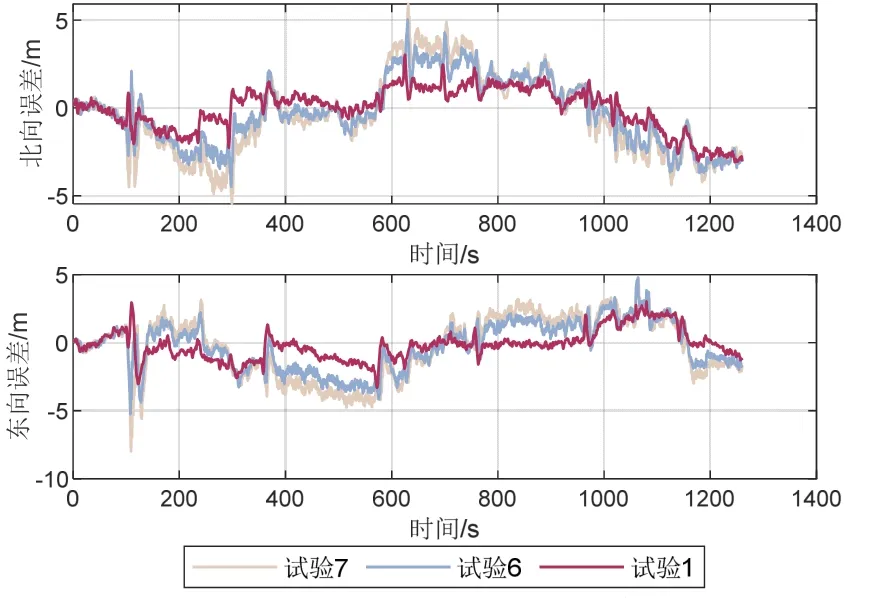
图12 试验1、6、7平面位置误差曲线对比Fig.12 Error curves of position error in experiment 1, 6, 7
以上分析可见,因子图算法凭借其可以在当前时刻追溯历史时刻的传感器状态的优势,当USBL信息滞后时间较短时,可以实现与没有滞后时相近的导航精度且计算量小,但是当USBL信息滞后时间较长时,修正效果变差但相比于曲线拟合法仍有明显改进。此外,在处理出序信息的表现上,因子图法也比弃用数据法解算效果更佳。
4 结 论
本文在考虑了AUV传感器信息滞后问题的前提下,采用因子图算法实现了基于SINS/USBL/DVL的多传感器信息融合定位,提出了对滞后信息的处理策略,并进行了试验分析并得出如下结论:当滞后传感器信息顺序到达时,相较于曲线拟合法,因子图匹配历史信息能够明显削弱时延不良影响,在USBL信息延迟1 s时精度提高12%,延迟5 s时精度提高52%,在滞后时间较长情况下更加优越,但长时间的误差积累使其相对于无滞后情况降低41.9%,可以针对该问题开展进一步研究;当滞后传感器信息出序到达时,相较于直接丢弃,因子图法能够迅速、完整地利用出序信息,提高19.7%的平面精度。综上,该算法可以有效补偿时延导致的精度下降,可以灵活应用于多种条件下的时延问题。
