基于混合人工鱼群算法的机器人路径规划研究

张 军 于士坤

（1.安徽理工大学人工智能学院；2.安徽理工大学机械工程学院 安徽淮南 232001）

移动机器人的路径规划是指在一个工作空间中，依据特定的优化准则（如行走成本最小、行走路径长度最短、耗费时间最少等），找到一条从起始位置到目标位置的最优路径,并且不能碰撞任何障碍物[[1]。目前，国内外学者针对路径规划问题进行了广泛探索并提出了诸多有效算法，如人工势场法[2]、遗传算法[3]、蚁群算法[4]、粒子群算法[5]、快速随机树算法[6]、人工鱼群算法[7]等。这些算法均能解决一定环境下的机器人寻路问题，但规划结果往往不是最优，需进一步研究改进。

文献[8]在传统蚁群算法中加入伪随机因子，减少了迭代次数、加快了收敛速度，有效提高了蚁群算法寻找路径寻优的效率。文献[9]在JPS算法基础上，提出以2个优化目标对路径点序列进行平滑处理的方法，并利用多段高阶多项式对所得轨迹进行优化，使路径长度得到减少，并明显提高了路径平滑性。文献[[10]针对A＊算法的水下重力匹配导航路径规划问题，通过前后向对比分析对单个路径节点逐个进行筛选过滤，有效减少了冗余航向调整，提高了算法效率和路径的平滑度。文献[11]使用神经网络改进了粒子群算法，改进后的算法在动态和静态障碍物环境中均可以高效规划出理想路径。文献[12]提出了无碰撞检测RRT算法，去除了RRT算法中的碰撞检测，在代价函数中引入风险评估函数，使改进后的算法大幅度提高了收敛速度，且具有良好适应性。文献[13]在无人机的路径规划问题中对遗传算法的选择、交叉和变异算子进行了改进，显著提高了算法的性能。文献[14]针对船舶航迹规划问题，在传统蚁群算法基础上提出了领头顶点蚁群算法，通过保证蚁群的领头并利用顶点法对路径进行优化，使算法耗费时间和路径航路点数量都得到减少。

人工鱼群算法是由李晓磊博士等人提出的一种群智能优化算法，通过模仿鱼群的聚群、追尾、觅食等行为寻找最优解，在机器人路径规划中取得了较好效果。但是，传统人工鱼群算法存在收敛速度较慢、寻优精度较低、规划出的路径折点多等不足[15]，通过将人工鱼与天牛须算法进行融合，利用动态人工鱼视野和动态拥挤度因子来平衡兼顾算法的全局收敛和局部搜索能力，以提高混合算法的寻优精度。将混合算法在不同规模的栅格地图中进行仿真验证，结果表明规划出的路径在长度和折点数发面均有明显改善。

一、基本人工鱼群算法

人工鱼群算法是通过观察模拟鱼群行为得出的优化算法。在某片水域里，鱼群往往集中在食物最丰富的地方，通过模仿鱼群的一些列行为便可以实现寻找最优解的目的。在鱼群中，每条鱼都具有觅食、聚群、追尾和随机四种行为，鱼类通过按照一定规则迭次进行这四种行为可以逐步趋向食物最优处（最优解）。

假设鱼群由S条人工鱼组成，向量X=（x1,x2,x3,…,xs）表示每条人工鱼个体的状态,其中i=1,2,3,…,S；Yi=f（Xi）表示人工鱼当前位置食物浓度，f（）为目标函数；人工鱼个体间距为dij=||xi-xj||；visual表示人工鱼的视野范围；δ表示拥挤度因子；step表示人工鱼的移动步长；try_number表示人工鱼进行觅食活动的最大尝试次数；rand为0到1之间的随机数。

（一）觅食行为。觅食行为表示人工鱼趋向高食物浓度方向的行为，状态为Xi的人工鱼个体在其视野范围内随机选择一个状态Xj，其适应分别计算适应度值并进行比较，若Yj优于Yi，则Xi向Xj方向移动一步，Xj更新为移动之后的新状态，否则重新觅食。

若尝试try_number次后仍未满足觅食前进的条件，则进行随机行为。

（二）聚群行为人工鱼鱼为保证自身生存和躲避危害会自然地聚集成群，聚群行为能够加强算法的全局收敛性。状态为Xi的人工鱼个体从当前当前位置视野内搜索到伙伴数目为Nf，并获取视获伙伴的中心位置Xc，若Yc/Nf优于δYi，表明中心位置状态较优且不太拥挤，则Xi向Xc位置方向移动一步，否则执行觅食行为。

拥挤度因子δ用来表示鱼群的拥挤程度，通多调整δ可以限制人工鱼的聚群规模，防止局部最优。

（三）追尾行为。追尾行为表示当某条鱼发现食物后，鱼群向其所在位置靠拢的行为。状态为Xi的人工鱼个体从当前位置视野内搜索伙伴数目Nf和状态最优个体Xj，Nf适应度值为Yj，若Yj/Nf优于δYi，表明Xj位置状态较优且不太拥挤，则Xi向Xj位置方向移动一步。否则执行觅食行为。

（四）随机行为。随机行为是觅食行为的一个缺省行为。当反复进行一定次数的觅食尝试后仍未满足移动条件时，人工鱼便会在视野范围内随机移动一步。随机行为能在一定程度上防止局部最优。

（五）公告板。公告板用来记录人工鱼的最优位置。人工鱼将每次行动所得位置与公告板中的位置进行比较，若新获得的位置状态更优秀，则将共告板中的位置进行更新，反之则不做处理。

二、天牛须算法

天牛须算法[16]是受到天牛觅食原理启发而开发的算法。与其他依靠种群智能的仿生算法不同，天牛须算法只需要一个天牛个体便可以完成寻优过程。天牛在觅食时会根据两侧触角来检测食物气味的强弱，从而选择前进方向。如果其中一侧检测到的状态较优，则向该侧方向前进一步，否则转向另一侧前进。当到达下一个状态位置时，天牛的转向是随机的，将重新根据两侧触角检测结果来决定前进方向。通过迭代前进，逐步接近目标点。天牛须算法的具体步骤为：

（1）为模拟搜索行为，随机生成天牛搜索的方向向量，并进行标准化

其中，n是待优化参数的维度。

（2）计算两侧触角的坐标

其中，xt为t时刻天牛质心的坐标，dt是t时刻质心到触角的距离，xl和xr分别为t时刻左右两侧触角坐标。

（3）根据两触角对应的适应度函数值，决定下一时刻的移动方向，并计算要到达的位置

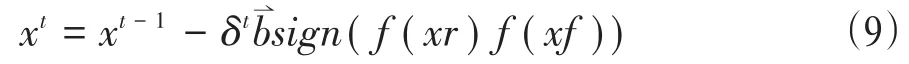
其中，δt为t时刻的移动步长，f为适应度函数。

（4）参数更新

其中，dt和δt分别是搜索距离和步长的更新衰减系数。

三、混合人工鱼群算法与栅格法

（一）混合人工鱼群算法。融合人工鱼群算法和天牛须算法的优点，利用天牛须算法对人工鱼群算法进行优化。传统人工鱼群算法存在较多随机性，在避免陷入局部最优的同时也会降低算法的收敛性，考虑天牛须算法全局收敛性强的优点，在聚群或追尾行为与后续的觅食和随机行为之间，加入一次人工鱼个体利用天牛须算法寻优的过程，以提高算法的全局收敛性。提出动态视野范围和拥挤度因子，使算法兼顾全局和局部收敛性。构想流程图如图1。

图1 混合算法流程图

每条人工鱼在寻优过程中分别从两个方向尝试，第一方向为：聚群行为、追尾行为、天牛寻优行为、觅食行为和随机行为；第二方向为：追尾行为、天牛寻优行为、觅食行为和随机行为。其间，每个方向的任一行为成功，则结束本方向流程，并在公告板更新结果；然后流程转到另一方向尝试。两个方向流程的尝试结束后，当前人工鱼移动到公告板所记录的位置，得到当前人工鱼本次寻优所得的最优位置。算法以第一条人鱼为寻优基准，当第一条人工鱼到达目标点时结束算法，否则，下一条人工鱼继续执行寻优过程。

（二）动态调整人工鱼视野和拥挤度因子。

1.动态视野。视野范围的大小直接影响到人工鱼的搜索能力。人工鱼在进行聚群、追尾、觅食和随机行为时，都需要在一定的视野范围内搜寻位置。基本人工鱼群算法中，视野参数被设为固定值。视野范围较大时，人工鱼的全局寻优能力强，但在接近目标点时的收敛能力弱；视野范围较小时，人工鱼后期收敛能力强，但全局寻优能力弱，且易陷入局部最优[17]。在混合算法中，通过引入下降函数来动态调整视野参数，使人工鱼的视野随着趋近目标值而逐渐下降，让算法兼顾全局搜索和在目标点附近的收敛能力。使用柯西-洛伦兹函数作为下降函数[18]，函数曲线如图4所示，当x0=0、γ=2时函数曲线下降较为平缓且下降幅度较小，适合用来调整人工鱼视野。柯西-洛伦兹函数的具体形式为：

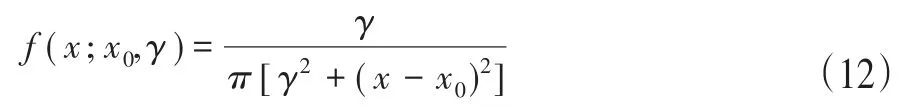
通过柯西-洛伦兹函数调节视野参数，有

其中，dig表示当前点与目标点之间的距离，dsg表示起始点与目标点之间的距离。

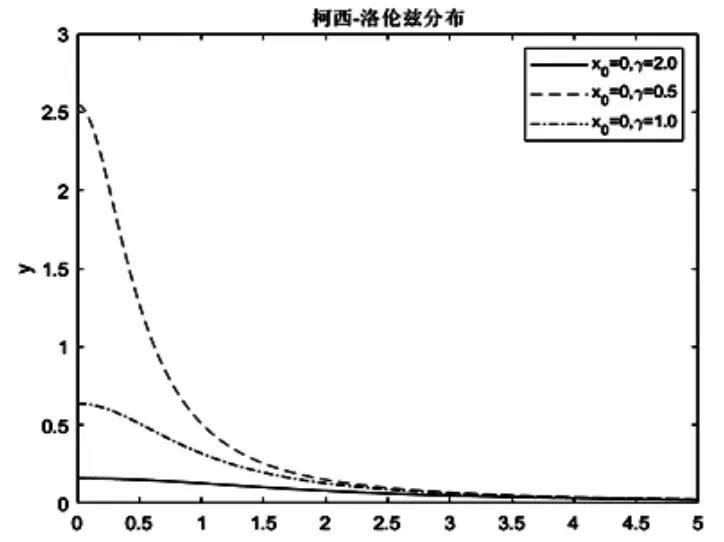
图2 柯西-洛伦兹分布

2.动态拥挤度因子。拥挤度因子δ表示一定范围内鱼群的拥挤程度，人工鱼在进行聚群、追尾和觅食行为时，都需要对搜寻所得点附近的拥挤程度进行判断。在路径规划问题中，δ越大表示允许的拥挤程度越大，有利于全局搜索但精度较差，反之则有利于提高收敛性局部搜索但易陷入局部最优。在混合算法中，引入放大系数Eδ使拥挤度因子δ随迭代次数增加而逐步增大，有

（三）在基本人工鱼群算法中引入天牛须算法。基本人工鱼群算法的寻优过程存在一定的随机性，为提高算法的全局收敛性，在寻优过程中引入天牛须算法。在人工鱼聚群或追尾失败后，先进行一次天牛寻优行为进行位置搜索，尝试利用天牛须寻优的方法进行一次移动，即

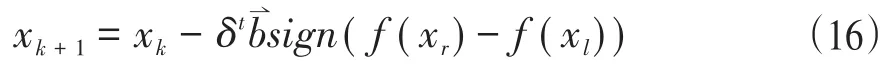
其中k表示天牛须搜索的迭代次数，xl和xr表示天牛左右须的位置。天牛寻优的流程图如图3。

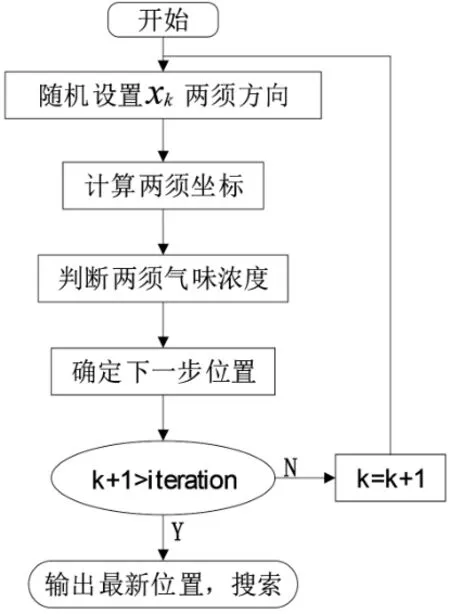
图3 天牛须算法流程图

若搜索成功则将所得位置更新到公告板，否则执行觅食和随机行为。

（四）适应栅格地图的混合算法。

1.栅格地图。采用栅格法建立地图模型，将移动机器人的行走环境空间由三维转换为二维并进行单元分割，将其用大小相等的方块表示出来。黑色方格表示障碍物，白色方格表示允许通行，如图4（a）所示。机器人只能在可行走栅格中通行，不能通过障碍物栅格。

对于每个栅格来说，其邻接的8个栅格为可行走栅格。相邻栅格的距离用中点的欧式距离表示，距离值为1或，如图4（b）所示。

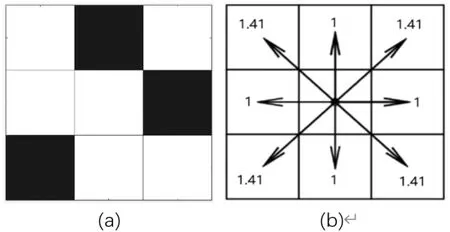
图4 栅格地图环境

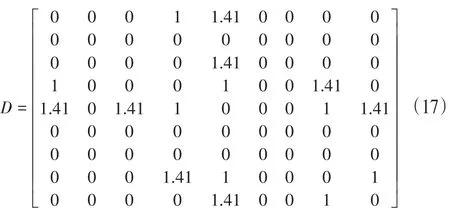
2.邻接矩阵。邻接矩阵是表示顶点之间相邻关系的矩阵。通过建立一个二维数组来存储栅格地图的信息，矩阵的规模为n2×n2，n为地图每一维的长度，n2表示地图中的栅格总数。每个栅格都有唯一对应的序列号，图5展示了栅格在地图中的标号排序方式。邻接矩阵的每一行存储了对应序列栅格与所有栅格的通行关系，障碍物栅格与所有栅格的关系值都为0；非障碍物栅格与邻接可行走栅格的关系值为1或，与非邻接栅格的关系值为0；所有栅格与本身的关系值为0。在栅格地图中，人工鱼的下一移动位置只会在与当前栅格关系值不为0的栅格中产生。以图1为例建立的邻接矩阵如公式（17）。

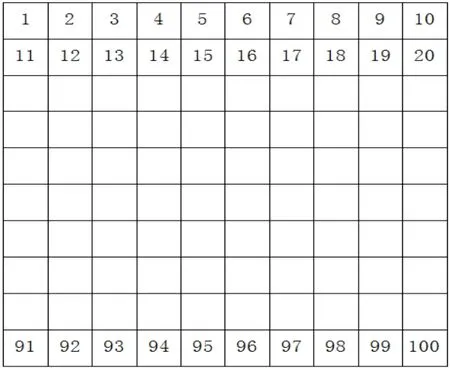
图5 栅格标识方法(xi,yi)

人工鱼在栅格地图中移动时，只可以在相邻的非障碍物栅格移动。设定每次移动的步长固定为1，在MATLAB仿真中，利用取整函数使人工鱼每次移动后的位置坐标为栅格左上角的点（用该点代表相应栅格）。人工鱼的可行域为与当前栅格在邻接矩阵中的关系值不为0的栅格。

通过适应度函数可以评价人工鱼位置的好坏，设人工鱼当前位置栅格坐标为（xi,yi），目标点位置为（xg,yg），则目适应度函数为：

（五）混合算法的具体实现步骤。如图1所示，改进算法实现的具体步骤为：

1.初始化参数，包括鱼群规模S，人工鱼视野Visual，拥挤度因子δ，拥挤度因子放大系数Eδ，人工鱼移动步长step，觅食最大尝试次数try_number，天牛法迭代次数bas_n，天牛步长bas_step，起点Xstart和终点Xgoal。

2.记第一条人工鱼为x1，设置其为位置为Pstart，随机设置其他人工鱼位置，记录每条人工鱼的位置及其适应度值。

3.当前人工鱼进行位置移动。每条人工鱼在当前位置分别进行两种选项的尝试。选项一：①执行聚群行为，若成功则更新公告板并跳出此选项，否则继续执行下一环节；②执行天牛寻优行为，若成功则更新公告板并跳出此选项，否则继续执行下一环节；③执行觅食和随机行为，更新公告板。选项二：与选项一相比除将环节①中的聚群行为变为追尾行为外，其余环节与选项一相同。

4.若当前人工鱼为x1，则将x1的位置加入路径path，判断人工鱼x1的位置是否为目标点位置，若是则结束算法并输出所得路径，否则按顺序更换人工鱼执行步骤3。

四、仿真实验

利用栅格法，在不同规模的地图环境分别进行基本人工鱼群算法和混合人工鱼群算法路径规划的仿真实验。建立30*30、50*50、100*100的栅格地图环境，初始参数：S=n，Visual=0.6×n，δ=0.618,step=1,try_number=10,起点Xstart为（1,1），终点Xgoal为（n,n），改进算法中，Eδ=1.019，天牛寻优迭代次数bas_iteration=50,天牛步长bas_step=1.5以上n表示栅格地图每一维的大小。在30*30地图环境中的试验结果如图6所示。

图6 30＊30地图路径规划结果

在50*50地图环境中的试验结果如图7所示。在30*30、50*50和100*100地图环境中均对两种算法进行20次随机试验。统计三种地图环境中基本算法和混合算法的路径信息，包括最长路径、最短路径、最大折点数、最小折点数、平均路径长度和平均折点数，得到三种地图环境的数据如表1-3所示。

图7 50＊50地图路径规划结果

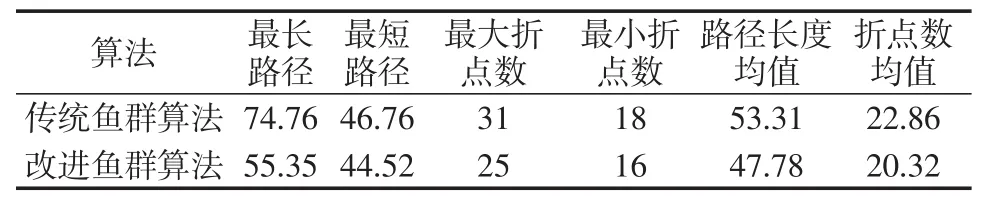
表1 30＊30栅格地图仿真结果

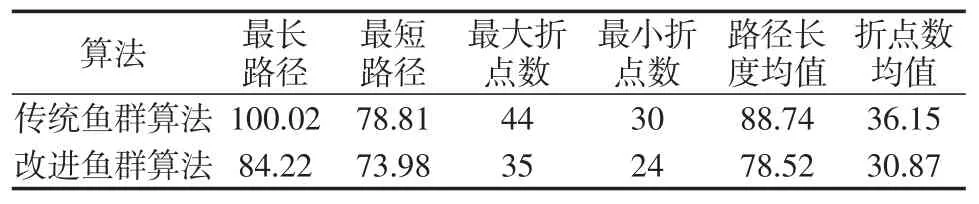
表2 50＊50栅格地图仿真结果

表3 100＊100栅格地图仿真结果

对比不同地图环境中的试验结果可见，混合算法规划出的路径明显优于基本人工鱼群算法，前者路径更短且折点数量更少。对于机器人而言，路径更短表示可以减少能量耗费、节约时间成本，折点数更少则表示可以减少机器人设备的磨损和消耗，延长使用寿命。

以100*100地图中的仿真结果表3为例，与基本人工鱼群算法相比混合算法的最长路径和最大折点数分别减少了29.90%和38.46%，最短路径和最小折点数分别减少了6.02%和23.07%，平均路径长度和平均折点数量分别减少了13.48%和19.74%。

考虑到仿真实验的随机性因素，平均路径长度和平均折点数更能代表算法的性能。根据表1-3，利用对应的优化率数据制成折线图，如图8所示。

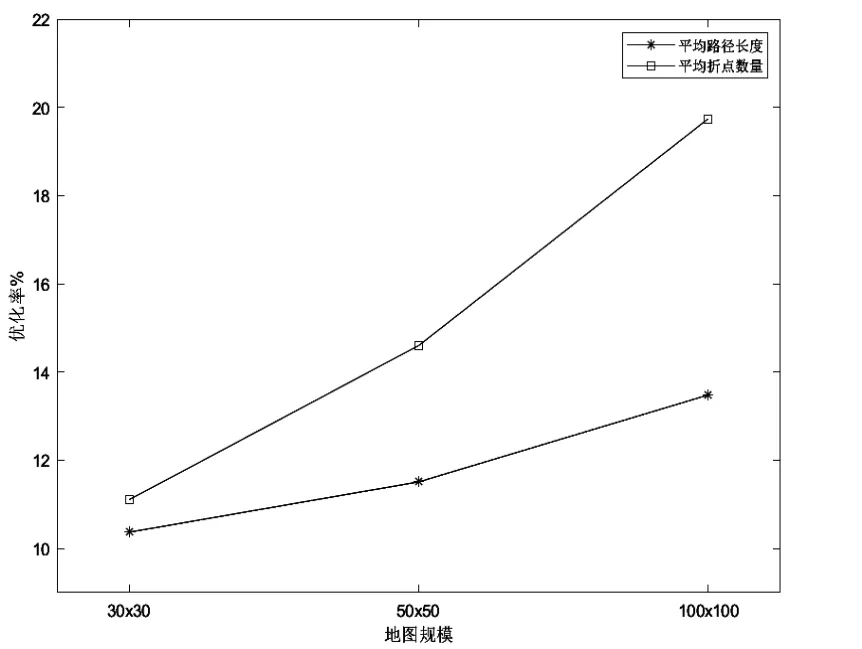
图8 混合算法对路径的优化程度

从图8可以看出，在不同地图中，相对于基本算法，利用混合算法规划出的路径平均路径长度和平均折点数都有明显改善，并且随着地图规模的增大，混合算法的优势也随之扩大。

五、结语

提出了混合人工鱼群算法，有效提高了人工鱼群算法的全局寻优能力，利用下降函数来逐步调整视野参数并提出动态拥挤度因子，使算法兼顾了全局搜索和在目标点附近的收敛能力。在30*30、50*50和100*100栅格地图环境中分别进行了20次随机仿真实验，数据显示混合算法规划出的路径与基本人工鱼群算法相比，三种栅格地图平均长度分别减少了10.37%、11.51%和13.48%，平均折点数量分别减少11.11%、14.60%和19.74%。

仿真实验的结果表明，在相同地图环境下混合算法规划出的路径更短，折点数更少，且随着地图的增大，优化效果逐渐提高。可以预见，在更大规模的地图环境中，混合算法将更具优势。