共轴刚性旋翼悬停状态桨叶表面压力测量试验与计算研究
2022-01-15江露生曹亚雄刘婷樊枫
江露生,曹亚雄,刘婷,樊枫
(中国直升机设计研究所直升机旋翼动力学国家级重点实验室,景德镇 333001)
共轴刚性旋翼高速直升机是当前及未来直升机的重点研究方向[1-2],其上下旋翼在大速度前飞时升力均向前行侧偏置,充分发挥前行桨叶[3]的气动性能,同时为后行桨叶卸载,推迟甚至避免后行桨叶的气流分离,减弱了后行桨叶动态失速的影响。同时,在高速飞行时,通过降低旋翼转速来减弱前行桨叶桨尖的空气压缩性影响,从而实现高速飞行[4]。
由于共轴刚性旋翼的气动原理与常规旋翼具有明显差别,其气动环境和特征与常规旋翼也有很大不同。由于上下旋翼反向旋转,且相距很近,下旋翼大部分区域处于上旋翼强烈的下洗流中,并且存在严重的涡-涡干扰、桨-涡干扰等复杂流动现象,共轴刚性旋翼气动环境是非常复杂的,即使是在悬停状态其流场也是高度非定常的。桨叶表面压力是能够反映桨叶表面流动和旋翼气动特性的重要物理量,为此,本文通过开展共轴刚性旋翼桨叶表面压力计算分析与试验研究,深入探索共轴刚性旋翼气动特性和桨叶表面流动状态,这对指导旋翼气动设计具有重要的学术意义和工程价值。
国外,特别是美国针对共轴刚性旋翼气动特性已经开展了较多的研究[5-9],但绝大多数都是针对共轴刚性旋翼气动性能、气动力、流场,而关于共轴刚性旋翼桨叶表面压力的试验研究却仍然很少。2016年,西科斯基飞机公司针对S-97的旋翼、桨毂、机身开展了缩比模型的气动特性风洞试验研究[10],并给出了少量的桨叶表面压力测量试验结果。国内,针对共轴刚性旋翼气动特性的研究起步较晚,不过在近几年发展较快,开展了一些理论[11-14]和试验[15-17]的研究,但尚未见公开发表共轴刚性旋翼桨叶表面压力测量试验研究的相关文献。
鉴于此,本文通过对4 m直径共轴刚性旋翼模型进行悬停状态桨叶表面压力测量试验,得到了上下旋翼桨叶不同剖面的表面压力数据,为其他数值建模研究提供了可靠的验证数据。在此基础上,根据试验结果,结合数值模拟方法,分析了上下旋翼桨叶表面的压力分布特性及气动干扰特性,得到了有意义的结论。
1 试验方法和内容
1.1 共轴刚性双旋翼试验台
本文试验使用的试验台如图1所示,其通过2个框式应变天平六分量天平分别对上下旋翼进行分开测力,主要部件包括电机、锥齿轮、内轴、外轴、轴承座、天平、滑油机,其中,内轴穿过轴承座内部,外轴中空套于轴承座外。对于此次表面压力测量试验,特别需要说明的是,上旋翼测压点压力数据采用集流环进行传输,下旋翼测压点压力数据采用无线的方式进行传输,无线遥测装置如图2所示。

图1 试验台及试验模型Fig.1 Experimental station and experimental model

图2 无线遥测装置Fig.2 Wireless telemetry device
本文试验采用微型压力传感器测量桨叶表面的非定常压力,传感器型号为kulit LQ-62型,压力传感器如图3所示。该型号传感器具有体积小、灵敏度高等优点,适用于本文桨叶表面压力测量试验。

图3 微型压力传感器Fig.3 Micro pressure sensor
试验台的数据采集处理系统由PXI系统组成,采集处理通道为96个,可进行方位角触发同步采集。上旋翼压力数据通过集流环传输的信号数据通过下方码盘给定触发信号进行采集,一圈采集64个点,一次采集80圈数据。下旋翼压力数据通过无线遥测传输,以固定2 000 Hz的频率进行采集传输,传输至数据采集处理系统中,进行插值处理成一圈64个数据点,一次采集80圈数据,一个遥测具有8个通道,为保证方位角的精确,方位定位触发信号需要占用1个通道,实际压力数据采集只有7个通道。
1.2 试验模型
本文试验的模型为4 m直径共轴刚性旋翼,具体参数如表1所示。

表1 旋翼参数Table 1 Rotor parameters
上下旋翼桨叶分别在展向位置r=0.5R和r=0.8R两个剖面上布有测压点,如图4所示。
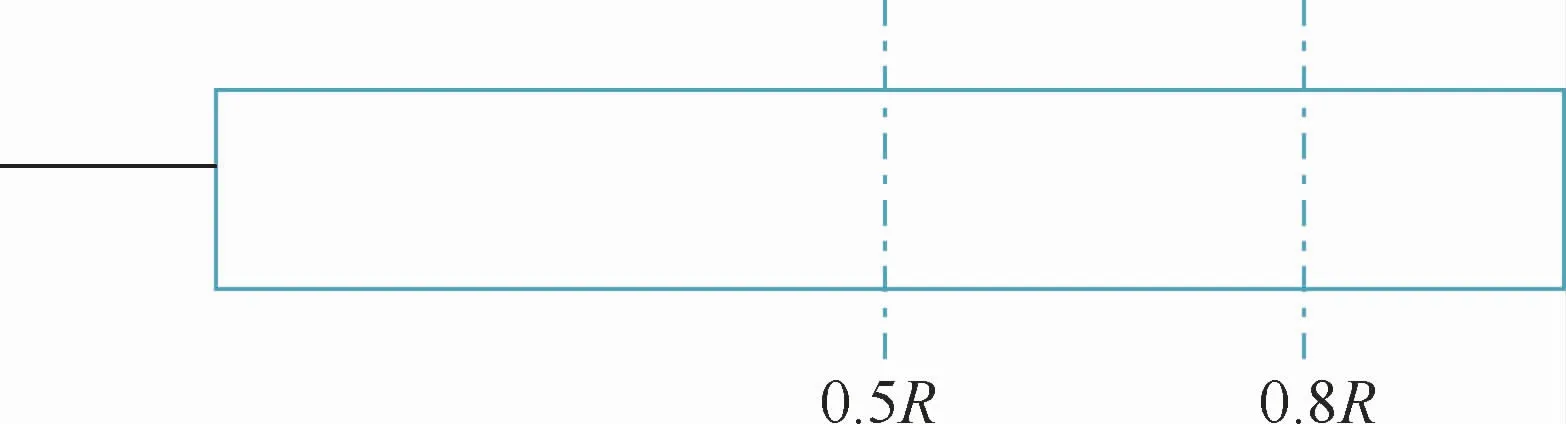
图4 剖面位置示意图Fig.4 Schematic diagram of profile location
上表面布置有5个测压点,下表面布置有3个测压点。测压点位置为:上表面:x/c=0.02、0.05、0.12、0.30、0.7;下表面:x/c=0.03、0.15、0.75。x为测压点距当地剖面前缘的距离,c为剖面位置对应的弦长。
1.3 试验内容
本文试验模型旋翼的额定转速为778 r/min,试验内容主要包括:测量悬停状态共轴双旋翼不同总距角配平状态(以上旋翼为准,φ0.7=5°、7°、9°、10°)下的上下旋翼桨叶表面压力数据,同时开展单旋翼悬停状态总距角(φ0.7=5°、7°、9°、10°)扫描桨叶表面压力测量试验。
2 数值模拟方法
由于试验中压力测量只有2个剖面位置,且每个剖面仅8个测压点数量,为更加全面地研究共轴刚性旋翼桨叶表面压力,本文同时采用了数值计算方法[18]进行了数值模拟,以深入研究共轴刚性旋翼桨叶表面压力的变化特性。
2.1 控制方程
由于共轴刚性旋翼上下旋翼气流相互干扰,不论是前飞还是悬停状态,都处于非定常状态,采用的控制方程为三维非定常雷诺平均Navier-Stokes(RANS)方程:

式中:W 为守恒变量;F(W)和G(W)分别为无黏通量和黏性通量。
为了减小物理耗散的影响及提高计算精度,采用低耗散的Roe格式,并结合MUSCL格式计算交接面上的无黏通量,同时采用物理时间和伪时间相结合的双时间方法进行时间步进。为了更好地捕捉黏性影响,采用了S-A一方程湍流模型。
与常规旋翼相同的是,共轴刚性旋翼各桨叶也存在旋转、变距等复杂运动。而与常规旋翼不同的是,共轴刚性旋翼2副旋翼反向旋转,且间距很小,上下旋翼存在复杂的气动干扰。因此,在生成网格时,上下旋翼桨叶网格要保持足够小的边界。为了准确模拟上下旋翼气动干扰流场,还要求在上下旋翼之间对背景网格进行加密,这也引起了网格量的剧烈增加,导致计算量增大。图5给出了共轴刚性旋翼嵌套网格示意图。本文计算采用的桨叶网格大小为175×43×95(弦向×法向×展向),背景网格大小为271×206×271(纵向×垂向×横向),对处于桨盘平面附近和桨尖附近的背景网格进行局部加密处理。

图5 共轴双旋翼嵌套网格Fig.5 Coaxial dual-rotor overset grids
2.2 共轴刚性旋翼悬停状态计算与试验对比
将本次试验测量得到的结果进行处理,将各个剖面测量得到的压力值P进行无量纲化得到

式中:ρ为空气密度;P为试验中测量得到的压力值;P0为试验开始前测量得到的压力初始值;Vr为对应剖面的相对来流速度。数值模拟得到的压力系数处理方式与试验一致。
首先,研究桨叶表面压力的计算与试验的对比情况,选取拉力系数为0.016 3的共轴双旋翼悬停状态在180°方位角的剖面压力分布。图6给出了配平状态上下旋翼在180°方位角桨叶表面压力计算与试验的对比曲线。图中:Cw为拉力系数。可以看出,上下旋翼的计算结果在0.5R剖面吻合得较好,而在0.8R剖面上,翼剖面压强分布吻合度略差。受上旋翼尾迹干扰,下旋翼桨叶0.8R~0.9R处的流动特征最为复杂,上旋翼收缩的尾迹与桨叶在该位置附近易发生垂直干扰[19],引起尾迹涡的破碎,破碎的涡会对局部的气动力产生影响。尾迹涡与桨叶的这种干扰过程是非定常的,在旋转周期上呈现一定程度的非稳态特性,这种特征也给试验的准确测量和数值模拟带来了困难,从而造成两者之间的误差。
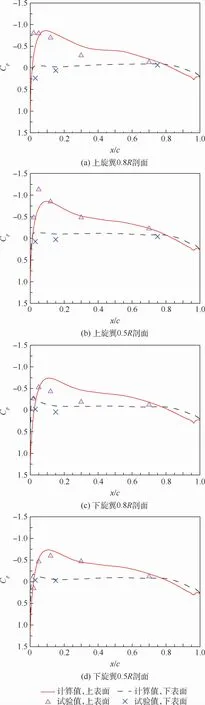
图6 桨叶表面压力系数计算与试验对比曲线(C w =0.016 3)Fig.6 Comparison of blade surface pressure coefficient between calculation and experiment(C w =0.016 3)
图7给出了下单旋翼悬停0.5R剖面压力系数试验结果与计算结果的对比曲线。可以看出,计算与试验吻合得很好。图8给出了单旋翼悬停0.8R剖面压力系数试验结果与计算结果的对比曲线。可以看出,0.8R剖面压力系数的计算结果与试验结果吻合度良好。无论是单旋翼还是双旋翼的计算与试验对比,吻合度均良好,可以看出数值模拟的精度较高,可有效进行共轴刚性旋翼桨叶表面压力特性计算研究。同时,互相验证了结果的可靠性,也为后续分析奠定了基础。
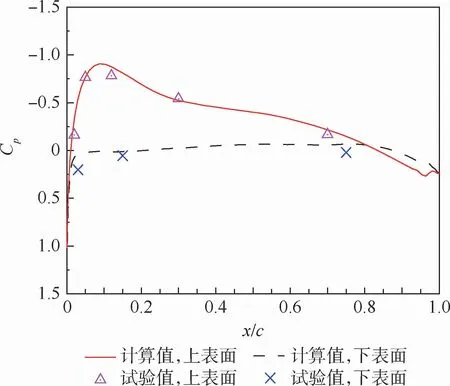
图7 桨叶0.5R剖面压力系数计算与试验对比曲线(C w =0.010 2)Fig.7 Comparison of pressure coefficient of 0.5R blade profile between calculation and experiment(C w =0.010 2)
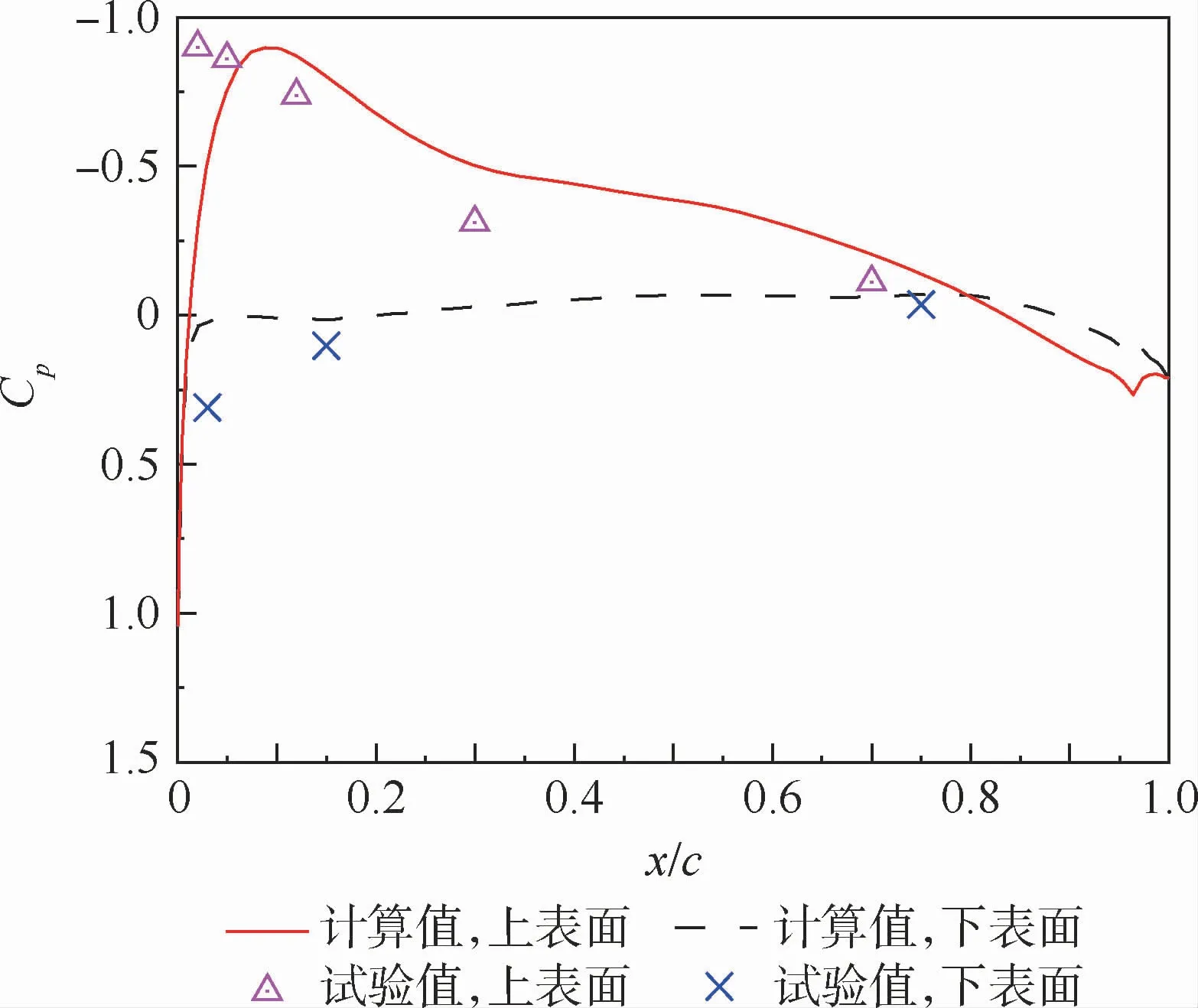
图8 桨叶0.8R剖面压力系数计算与试验对比曲线(C w =0.010 2)Fig.8 Comparison of pressure coefficient of 0.8R blade profile between calculation and experiment(C w =0.010 2)
3 试验与计算结果分析
3.1 配平状态桨叶表面压力特性
为观察共轴双旋翼桨叶表面压力旋转一周的变化曲线,在旋转一周采集64个点的情况下,选取试验配平状态上下旋翼桨叶0.8R和0.5R剖面上表面0.02c测压点,压力变化曲线如图9和图10所示(图中:φ为方位角)。可以看出,上旋翼的上表面2个测压点的压力变化在一个旋转周期内存在8个明显的小周期,这是由于上旋翼的桨叶与下旋翼桨叶在一圈内相遇8次,会出现8次明显的瞬时压力变化,下旋翼桨叶表面压力亦是如此。
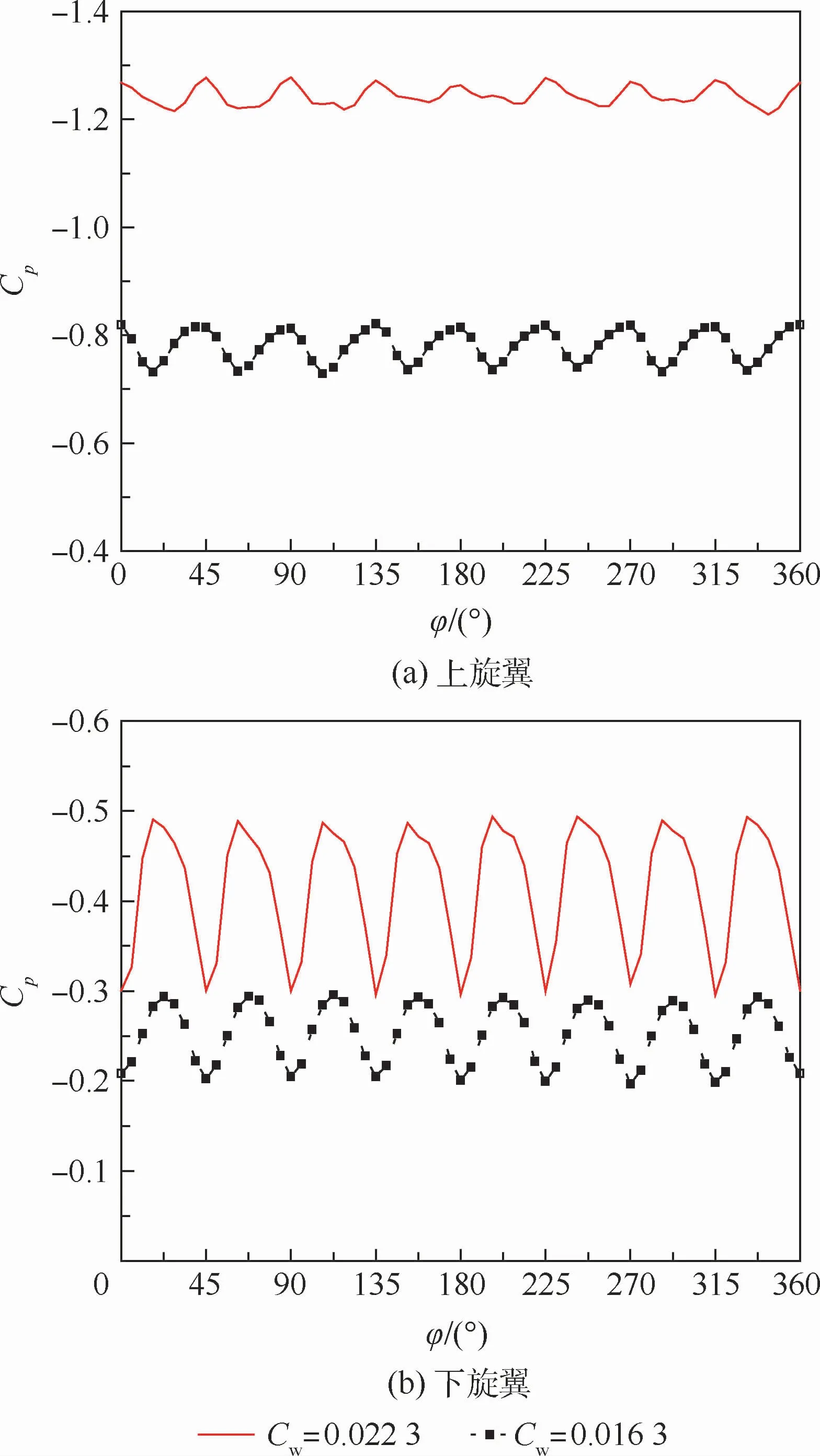
图9 桨叶0.8R剖面测压点压力系数随方位角变化曲线(试验值)Fig.9 Pressure coefficient variation with azimuth angle at pressure measuring point of 0.8R blade profile(experiment value)
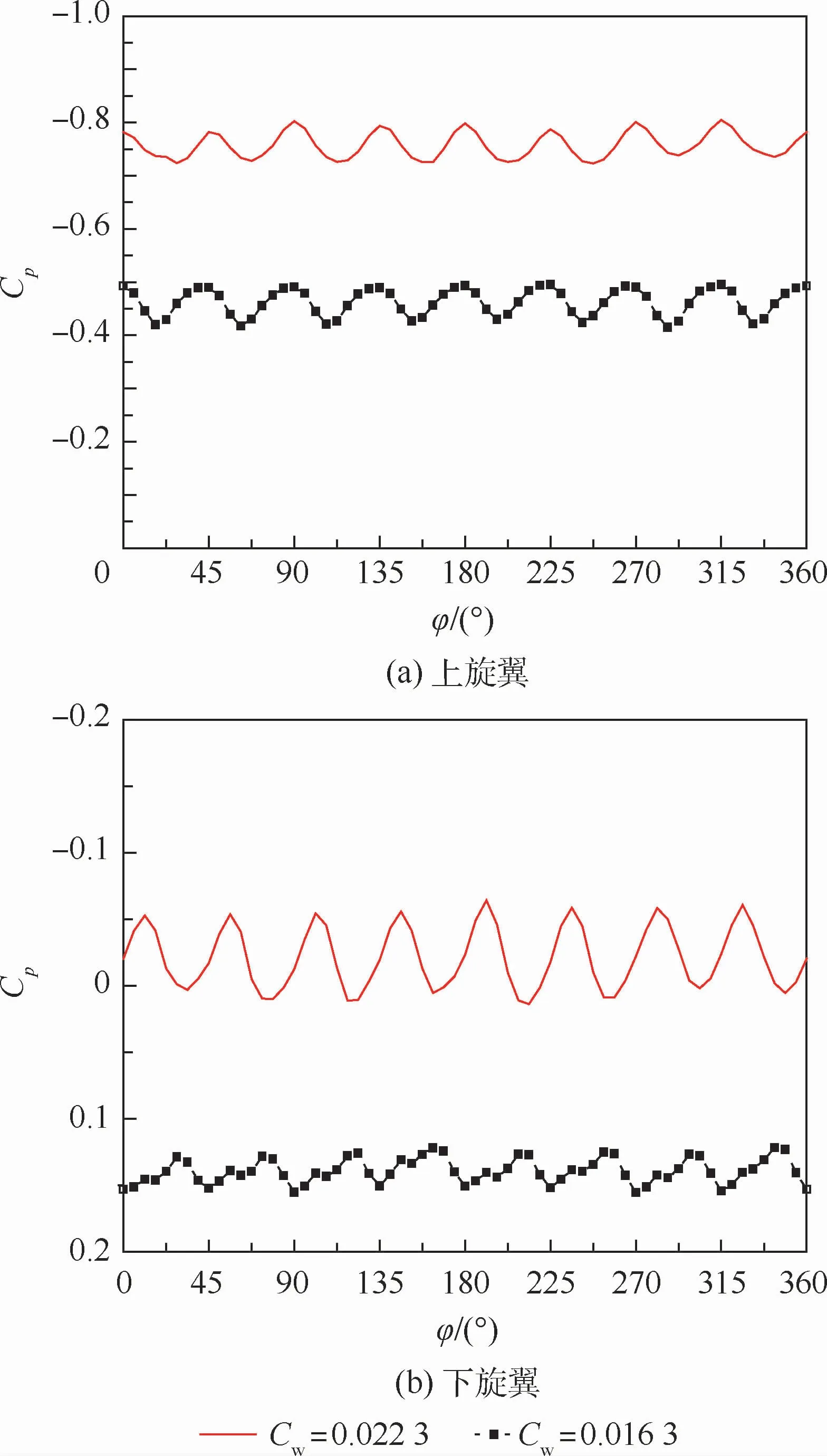
图10 桨叶0.5R剖面测压点压力系数随方位角变化曲线(试验值)Fig.10 Pressure coefficient variation with azimuth angle at pressure measuring point of 0.5R blade profile(experiment value)
从0.5R和0.8R剖面的下旋翼0.02c测压点的不同拉力系数下压力变化可以看出,下旋翼受到上旋翼下洗流的影响,拉力增大,压力系数波动的幅值也会明显增大。但0.5R的测压点压力随着拉力系数增大的幅值变化没有0.8R剖面的大,这是由于下旋翼0.8R剖面不仅受到下洗流的影响,还受到桨尖涡的影响。而上旋翼2个剖面0.02c测压点的压力随着旋翼拉力系数增大幅值变化没那么明显。
本文试验状态及结果有限,为进一步分析桨叶表面压力特性,开展相关的计算研究。首先,分析共轴双旋翼配平状态(上下旋翼扭矩平衡)的桨叶表面压力特性,此时上下旋翼总距角分别为8°和9°,上旋翼拉力系数为0.008 82,下旋翼拉力系数为0.007 46。可以看出,下旋翼的总距角虽然比上旋翼要大,但拉力却要小于上旋翼。图11给出了配平状态上下旋翼桨盘的拉力分布云图。可以看出,下旋翼桨盘的大部分区域拉力小于上旋翼,说明此时上下旋翼存在明显的气动干扰,且下旋翼受到的干扰影响较大。

图11 配平状态桨盘拉力分布Fig.11 Distribution of disc traction in trimmed state
图12给出了配平状态上下旋翼径向剖面的轴向诱导速度V云图。可以看出,下旋翼桨叶比较大的一部分区域(0.4R~0.9R)的诱导速度明显要大于上旋翼桨叶,诱导速度的增大使得桨叶的有效迎角减小,这也就导致下旋翼总距角虽然大于上旋翼,但拉力明显低于上旋翼。而桨尖部分区域的流场主要受到各自桨尖上洗流的影响,桨叶周围的诱导速度场的变化必然会影响桨叶表面的压力变化。由于桨叶不同剖面位置受到的轴向诱导速度不一致,计算了0.5R、0.8R和0.98R三个剖面位置前缘区域的压力云图,如图13所示。可以明显看出,在桨叶0.5R和0.8R上旋翼桨叶上表面的低压区域明显多于下旋翼,而在0.98R出现相反的结果,翼型剖面的压力大小直接影响了剖面的升力,如图14所示。可以看出,上下旋翼压力系数差异主要在前缘区域,也是翼型的主要升力段。在0.5R和0.8R剖面位置的上旋翼桨叶压力系数的负压峰值大于下旋翼,而下旋翼在0.98R剖面位置的升力大于上旋翼,主要是因为0.98R处下旋翼的总距角大于上旋翼,且此时主要受到各自上洗流的影响。

图12 上下旋翼轴向诱导速度云图(180°方位角)Fig.12 Axial induced velocity contour of upper and lower rotor(180°azimuth angle)
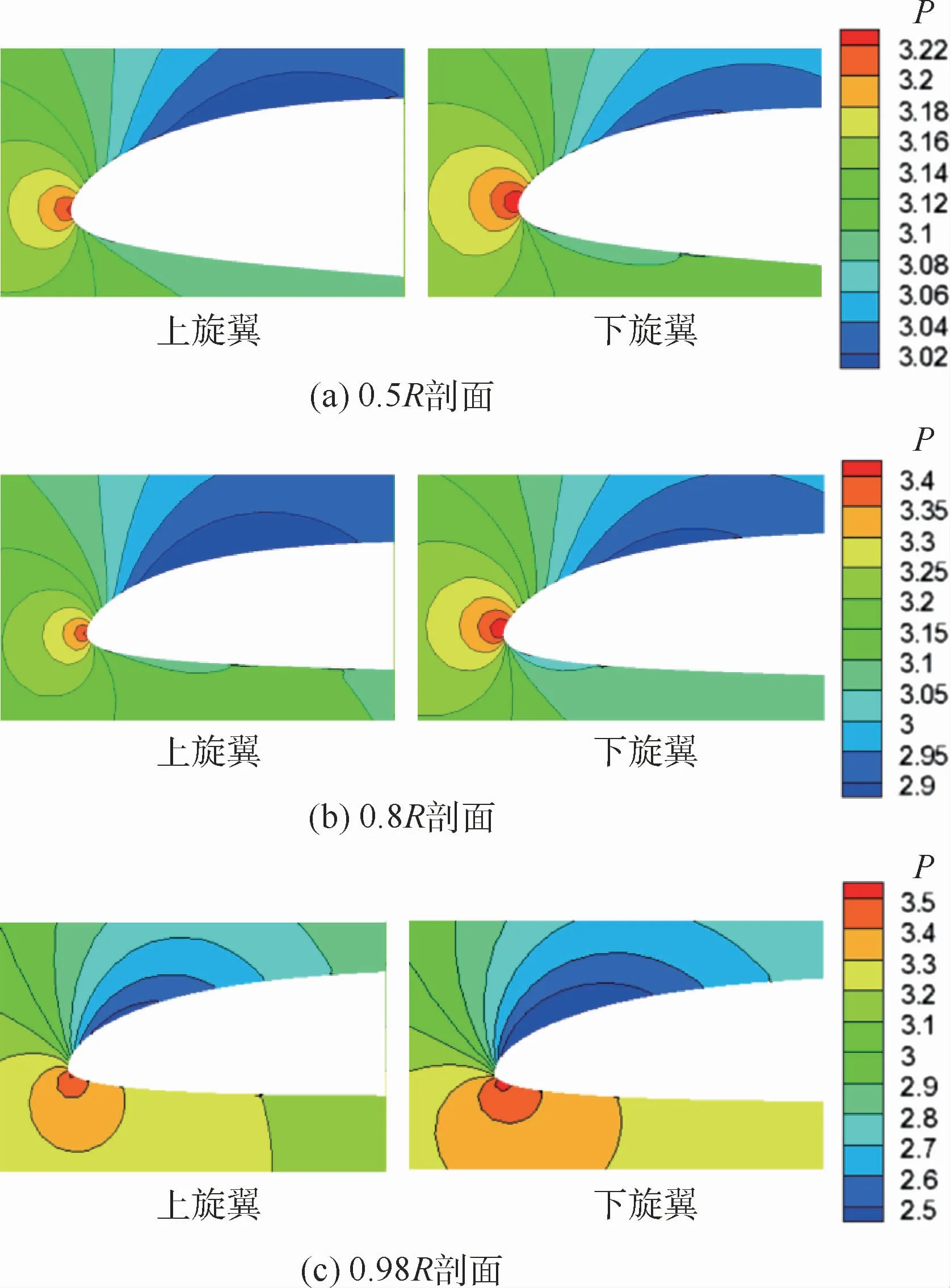
图13 上下旋翼剖面压力云图(180°方位角)Fig.13 Profile pressure contour of upper and lower rotor(180°azimuth angle)

图14 不同剖面位置压力系数分布(180°方位角)Fig.14 Pressure coefficient distribution at different profile positions(180°azimuth angle)
共轴双旋翼上下旋翼反向旋转,因此上下旋翼桨叶表面的压力也是非定常的。图15给出了上下旋翼桨叶0.5R剖面位置不同弦向位置点的压力系数随方位角变化曲线。可以看出,桨叶表面的点,无论是靠近前缘还是后缘,压力均随着方位角呈周期性变化,由于上旋翼一片桨叶与下旋翼桨叶在一圈内相遇8次,会出现8次明显的瞬时压力变化,而且整体来看上旋翼的压力脉动幅值要高于下旋翼。

图15 不同弦向位置点压力系数随方位角变化曲线(C w =0.016 3)Fig.15 Pressure coefficient variation with azimuth angle at different chordwise positions(C w =0.016 3)
3.2 相同总距角状态下桨叶表面压力特性
为更好研究共轴刚性旋翼上下旋翼气动干扰情况,选取上下旋翼总距角均为9°及单旋翼总距角为9°状态下的桨叶表面压力进行对比,此时上旋翼拉力系数0.010 8,下旋翼拉力系数0.006 5,单旋翼拉力系数Cw=0.012 0,上旋翼拉力与单旋翼接近,而下旋翼拉力远低于二者。图16给出了上下旋翼和单旋翼均为9°总距角状态下的桨盘拉力分布云图。可以看出,上下旋翼存在明显的气动干扰。

图16 同总距角状态桨盘拉力分布Fig.16 Distribution of disc traction at the same total pitch angle
图17给出了上下旋翼和单旋翼的拉力系数随着方位角变化曲线,单旋翼的拉力系数近乎一条直线,而上下旋翼的拉力系数则随着方位角呈周期性变化,旋转一圈,呈现出8个小周期。

图17 同总距角状态拉力系数随方位角变化曲线Fig.17 Traction coefficient variation with azimuth angle at the same total pitch angle
图18给出了相同总距角状态下不同剖面的压力系数分布计算结果。可以看出,0.5R和0.8R上旋翼剖面的压力系数与单旋翼比较接近,但整个剖面的拉力在几个剖面位置均低于单旋翼,而下旋翼剖面拉力比上旋翼小得较多。在桨尖部分,0.98R剖面位置上下旋翼的压力系数非常接近,但负压峰值还是略低于单旋翼,此时桨尖区域上下旋翼存在一定的干扰,但干扰相对较小。
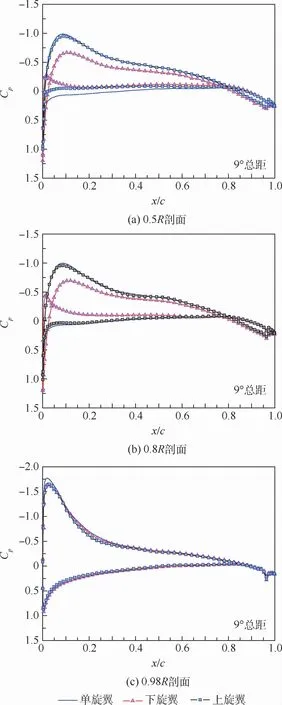
图18 同总距角状态不同剖面位置压力系数分布(180°方位角)Fig.18 Pressure coefficient distribution at different profile positions at the same total pitch angle(180°azimuth angle)
图19给出了0.5R剖面桨叶上表面弦向位置0.02c和0.3c的压力系数随方位角变化曲线。上旋翼呈现比较清晰的周期性,而下旋翼受到的干扰较大,剖面的压力系数随着方位角波动更为明显,而单旋翼波动很小,近乎是一条直线。
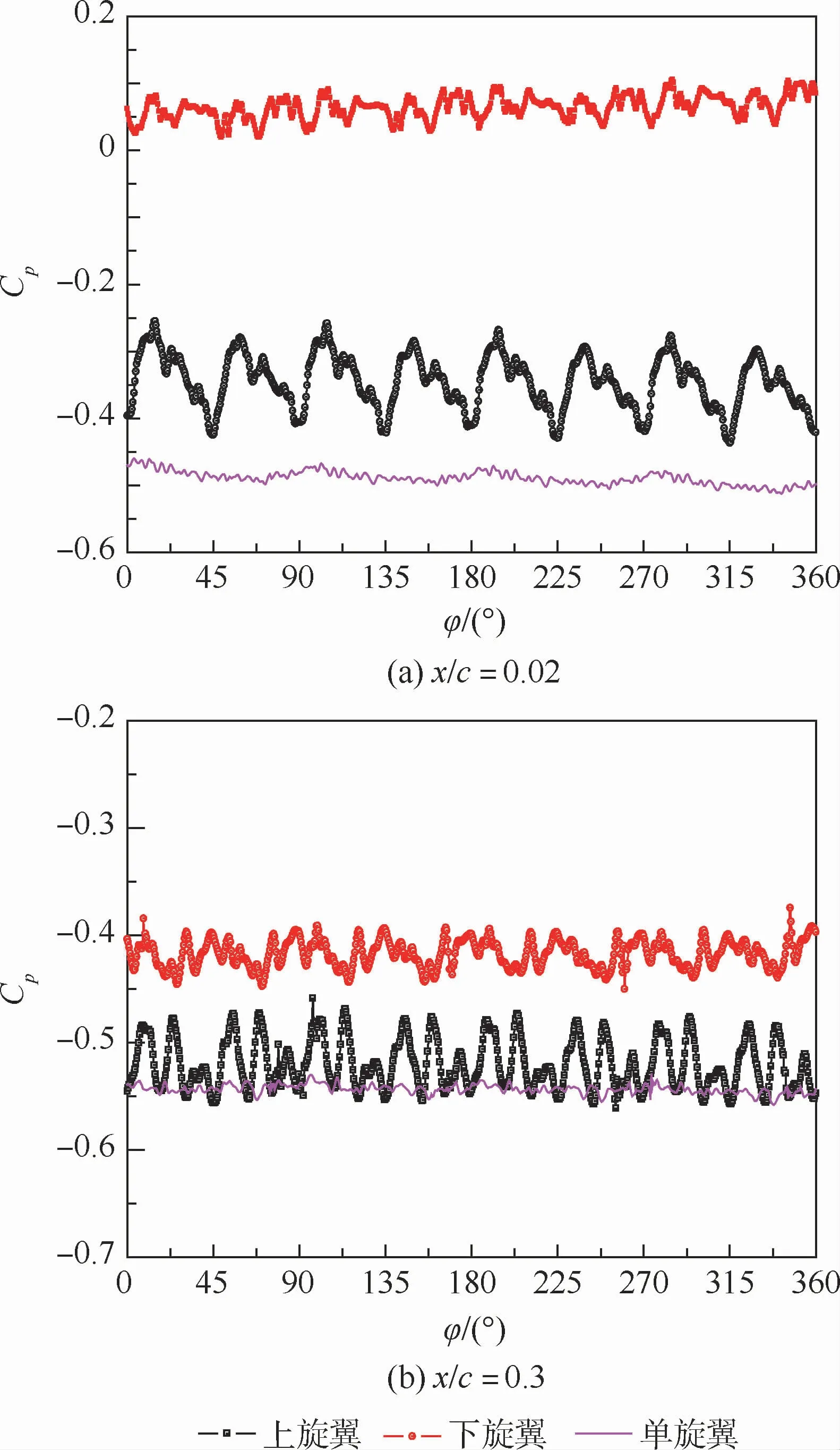
图19 剖面点压力系数随方位角变化曲线Fig.19 Pressure coefficient variation with azimuth angle at profile measuring point
4 结 论
本文针对共轴刚性模型旋翼悬停状态桨叶表面压力进行了试验与计算结果分析研究,得出以下结论:
1)获得了共轴刚性旋翼桨叶表面非定常压力变化试验数据,并验证了计算模型的有效性。
2)对于上下旋翼各4片桨叶的共轴双旋翼悬停状态,桨叶表面压力随着桨叶旋转呈周期性变化,桨叶旋转一周,压力变化8个小周期,而且上旋翼的压力脉动幅值高于下旋翼。
3)在配平状态,下旋翼的总距角大于上旋翼,而下旋翼桨叶大部分区域受下洗流影响,使得下旋翼剖面拉力低于上旋翼;桨尖区域主要受到各自上洗流的影响,使得下旋翼桨尖部分的升力高于上旋翼。
4)相同总距角状态下,大部分区域上旋翼的剖面负压峰值接近单旋翼,但远高于下旋翼;而桨尖区域上下旋翼桨叶剖面的负压峰值基本一致,但还是略低于单旋翼。
