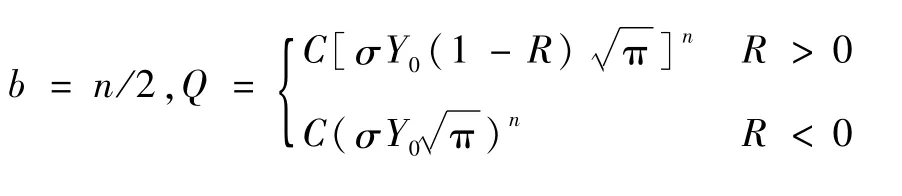耐久性分析相对小裂纹扩展速率公式的参数确定方法
2022-01-15左冉东贺小帆李玉海
左冉东,贺小帆,李玉海
(北京航空航天大学航空科学与工程学院,北京 100083)
飞机结构在使用过程中长期承受交变载荷作用,由此造成的疲劳断裂是飞机结构最主要的失效模式,为了保证飞机结构的使用安全和经济性,应进行耐久性分析确定结构的经济寿命[1]。概率断裂力学方法是一种有效的耐久性分析方法,该方法基于描述结构原始疲劳质量的当量初始缺陷尺寸(EIFS)分布给出损伤度随时间变化的函数关系,进而依据指定的损伤度要求预测结构的经济寿命。在该方法中,原始疲劳质量和使用期裂纹扩展控制曲线(SCGMC)的确定都需要建立结构细节相对小裂纹扩展速率公式[2],因此相对小裂纹扩展速率公式的研究非常重要。
按几何尺寸不同,疲劳裂纹可分为小裂纹和长裂纹。一般而言,小裂纹是指裂纹长度小于几百微米的裂纹,而长裂纹则是指长于2 mm的裂纹[3]。受裂尖应力场的影响,小裂纹和长裂纹的扩展规律不同,需要分别描述[4-5]。而结构耐久性分析针对的多是长度小于或等于工程可检裂纹尺寸的裂纹,其长度一般在0.1~1.2 mm 范围内,通常称为相对小裂纹[6]。目前,已经对相对小裂纹范围内的裂纹扩展规律进行了大量研究。Frost和Dugdale[7]指出等幅载荷下,裂纹长度随载荷循环数的变化可用对数线性关系来表征。Barter等[8-9]基于大量的试验数据指出Frost和Dugale[7]的结论符合F/A-18和Macchi飞机中的7050铝合金的裂纹扩展行为。Molent等[10-11]对随机谱下多个飞机型号结构疲劳断口数据的分析也验证了该结论的正确性。
Yang等[12]在进行飞机结构耐久性分析时,认为相对小裂纹扩展速率与裂纹长度的常数幂线性相关,其中这个常数与材料有关,并用以确定EIFS分布。Gallagher和Stalnaker[13-14]基于孔边角裂纹扩展数据分析,验证了Yang等[12]结论的有效性。Hoeppner和Krupp[15]通过对大量裂纹扩展模型的对比分析,验证了该结论的正确性。
尽管大量的试验数据已经证明了Yang等[12]所提相对小裂纹扩展速率公式的有效性,且该公式在概率断裂力学方法中具有非常重要的作用,但仍存在如下问题:
1)该公式的适用范围不明确,相对小裂纹尺寸范围与细节几何尺寸有关,目前只能从试验数据的规律予以确定,缺乏统一的确定方法。
2)该公式中参数的确定基于耐久性试验,需要取结构细节模拟试件进行至少3个应力水平下的成组耐久性试验,试验工作量大。
为了建立相对小裂纹扩展速率公式中参数的确定方法,本文以受远场均匀拉伸载荷作用的中心圆孔板为分析对象,通过对材料裂纹扩展速率公式的分析、裂纹扩展分析的数值模拟、典型结构细节耐久性试验,以及该式适用范围的统一标准,得到参数Q和b的确定方法。
1 相对小裂纹扩展速率公式分析
按飞机结构设计思想,耐久性分析的对象是除飞行安全关键件外的结构关键件,这些关键件通常承受较高应力水平且存在应力集中,其疲劳失效对飞机结构的经济性造成严重影响,在全寿命周期内需要进行修理才能满足寿命指标要求[16-17]。因此,在相对小裂纹扩展范围内,其裂纹扩展过程主要集中在材料的稳定裂纹扩展段。材料疲劳裂纹扩展的d a/d N-ΔK曲线在双对数坐标下成“S”型,可分为3个阶段,其中第2个阶段,即稳定扩展区,一般可用Paris公式来表征:

当裂纹长度相对较小时,与Y0相比,式(3)等号右侧第2项为小量,即存在au,当a≤au时,可仅保留式(3)等号右侧第1项,即有

需要指出的是,Q为d a/d N=Qab中的系数;au取值与具体分析对象有关,可根据Y的变化情况,按工程许用误差(如±5%)予以确定。
2 远场均匀拉伸中心圆孔板相对小裂纹扩展速率公式参数确定
中心圆孔板在远场均匀拉伸载荷作用下,孔边会出现多种形态的裂纹,如孔边角裂纹、孔壁裂纹等。在相对小裂纹范围内,裂纹均为三维裂纹,应力强度因子求解复杂。本节针对典型裂纹形态,分有近似解和没有近似解2种情况进行研究。
2.1 基于应力强度因子近似解的参数确定
Shah[18]、Raju和Newman[19]使用有限元法得到了中心圆孔有限宽板孔边单边/双边角裂纹的应力强度因子解。Raju和Newman[20]基于有限元解得到了单边/双边角裂纹、单边/双边孔壁裂纹的应力强度因子近似解。
取3种中心圆孔有限宽板,模型尺寸如表1所示。在单侧孔边设置长度为0.1 mm的1/4圆形初始角裂纹,基于单边角裂纹的应力强度因子近似解[20]进行裂纹扩展分析。其中裂纹速率Paris公式参数为C=1×10-10、n=2,交变应力比R=0.1,峰值应力为98 MPa。经裂纹扩展分析得到a-N、a-Y数据,使用式(10)所示割线法计算裂纹扩展速率d a/d N(单位为mm/cycle,其中cycle为载荷循环次数,L为裂纹扩展过程中,相对小裂纹尺寸范围内的(a,N)数据对总数)。d a/d N-an/2曲线和a-Y曲线如图1(a)和图1(b)所示。
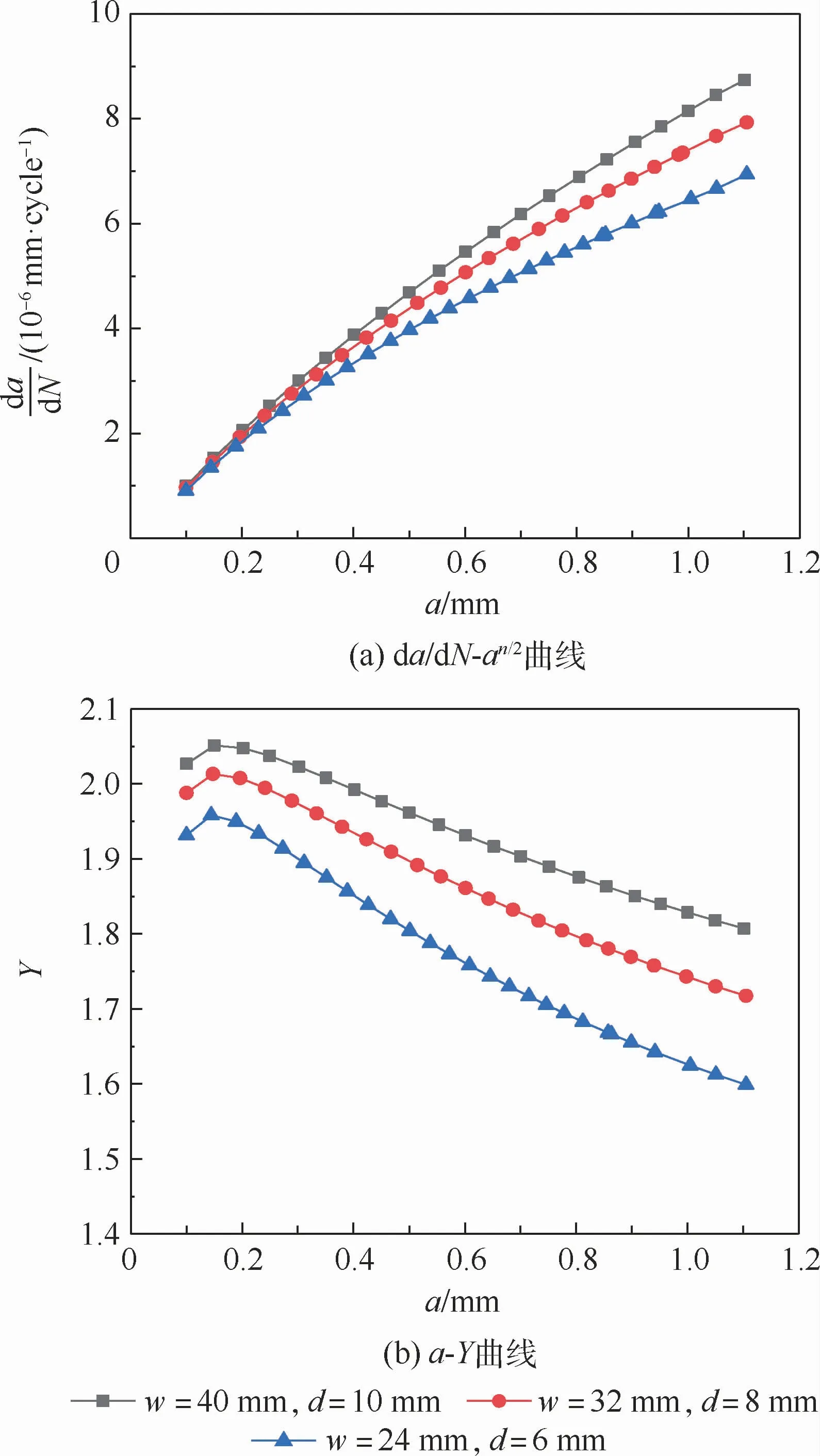
图1 基于应力强度因子近似解的裂纹扩展分析结果Fig.1 Analysis result of crack propagation based on approximate solution of stress intensity factor
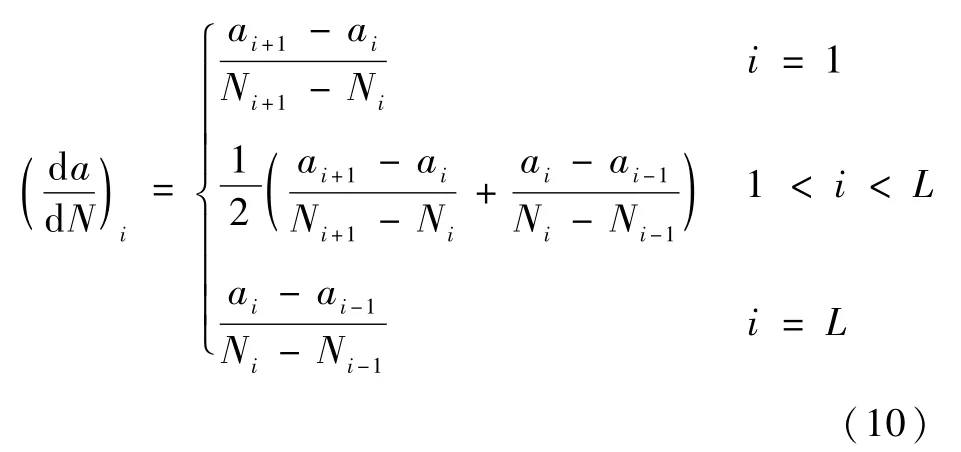
以Y与Y0的差值不超过±5%为依据确定au,各模型对应的au和Y0如表1所示。
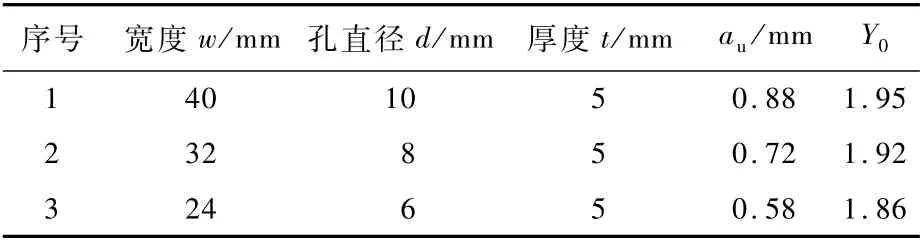
表1 模型尺寸Table 1 Model dimension
对a<au范围内的d a/d N-an/2数据进行线性拟合,斜率即为Q,拟合结果如表2所示,其中r2为相关系数。将参数C、n、σ、R和Y0代入式(9)计算Q值,记为Q′,按式(11)计算Q值的相对误差η,将Q′和η一并列入表2中。
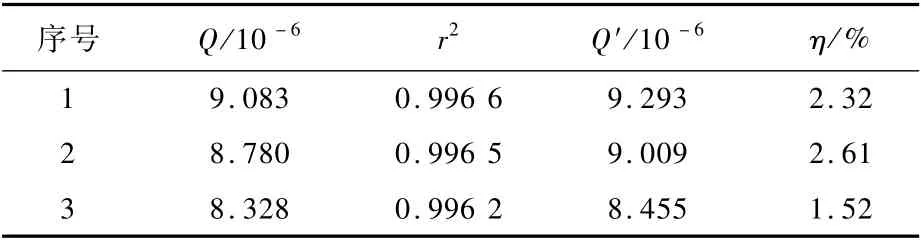
表2 da/dN-an/2数据处理结果Table 2 da/dN-an/2 data processing result

显然,在a<au范围内,d a/d N-an/2数据线性度良好,有式(8)成立;Q与Q′在误差许可范围内,有式(9)成立。
2.2 基于FRANC3D软件裂纹扩展分析的参数确定
2.1节针对有应力强度因子近似解的情况,阐明了相对小裂纹范围内式(7)的适用性和参数确定方法。由于中心圆孔平板试件在交变载荷作用下孔边会出现复杂的裂纹形态,本节针对没有应力强度因子解的情况,借助FRANC3D软件,模拟不同情况下的裂纹扩展并讨论参数的确定方法。
模型尺寸:宽度w=40 mm,孔直径d=10 mm,厚度t=5 mm。载荷谱和裂纹扩展速率参数同2.1节。以孔壁到裂纹前缘的径向最远距离为裂纹长度a,以模型一侧表面为参考表面,用初始裂纹中心到参考表面的距离x来表示初始裂纹中心的位置,如图2所示。
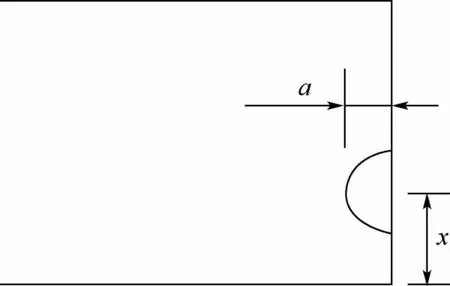
图2 裂纹描述示意图Fig.2 Schematic diagram of crack description
本节考虑如下4种裂纹扩展模式:①单边裂纹。②双边对称裂纹。这2种情况下,在孔侧x=0,1,2,2.5处分别设置初始长度为0.1 mm的半圆形或1/4圆形初始裂纹。③双边裂纹(位置不对称但初始长度相同),在孔壁两侧分别取x=0,1,2,3,4,5六个点为初始裂纹位置,两两搭配,考虑结构的对称性(如x=0与x=5位置,x=1与x=4位置是等效的)并剔除两边对称的搭配,还剩余9种搭配,如表3所示。④双边裂纹(初始裂纹尺寸不相同,位置对称)。在孔两侧x=0,1,2,2.5处分别设置半径为0.1 mm 和0.05 mm,0.2 mm和0.02 mm的圆形裂纹。采用FRANC3D软件模拟裂纹扩展并得到(a,N)数据,采用修正的割线法获得裂纹扩展速率d a/d N,各情况的d a/d N-an/2曲线如图3所示,其中对于双边裂纹(初始裂纹尺寸不相同,位置对称),仅对裂纹较长一侧的裂纹扩展结果进行分析。图3(c)图例含义为:一侧初始裂纹位置x-另一侧初始裂纹位置x-该曲线对应一侧的初始裂纹位置。
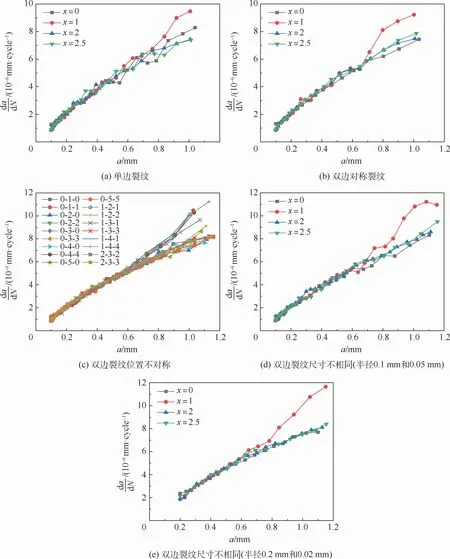
图3 基于FRANC3D模拟的d a/d N-an/2曲线Fig.3 d a/d N-an/2 curves based on FRANC3D simulation
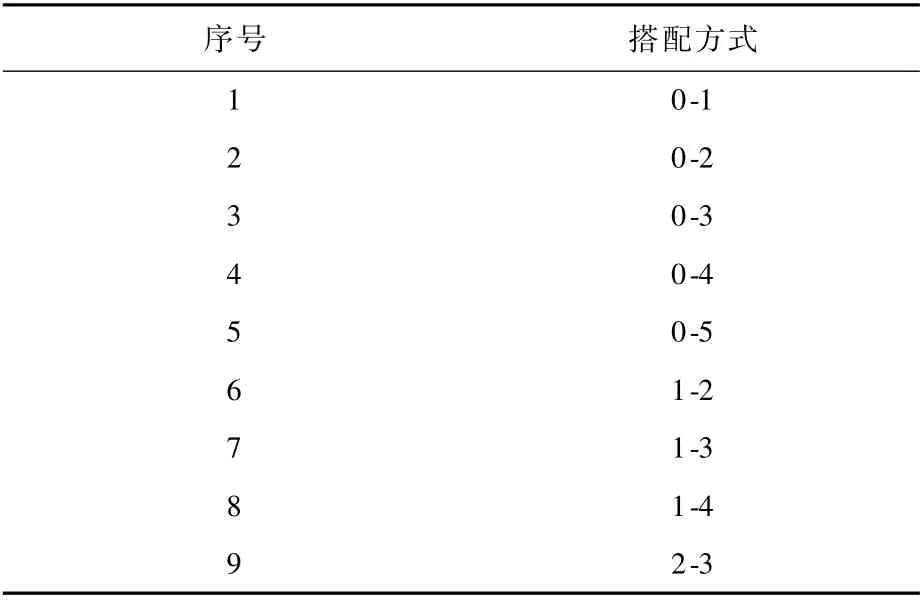
表3 初始裂纹位置搭配Table 3 Initial crack position collocation
取相对小裂纹的尺寸范围为a<0.88 mm、Y0=1.95(见表1)。对a<0.88 mm 范围内的d a/d N-an/2数据进行线性拟合,取截距为0,斜率即为Q,拟合结果如表4所示。将参数C、n、σ、R和Y0代入式(9)计算Q′,可得Q′=9.29×10-6。由此计算η,一并列入表4。
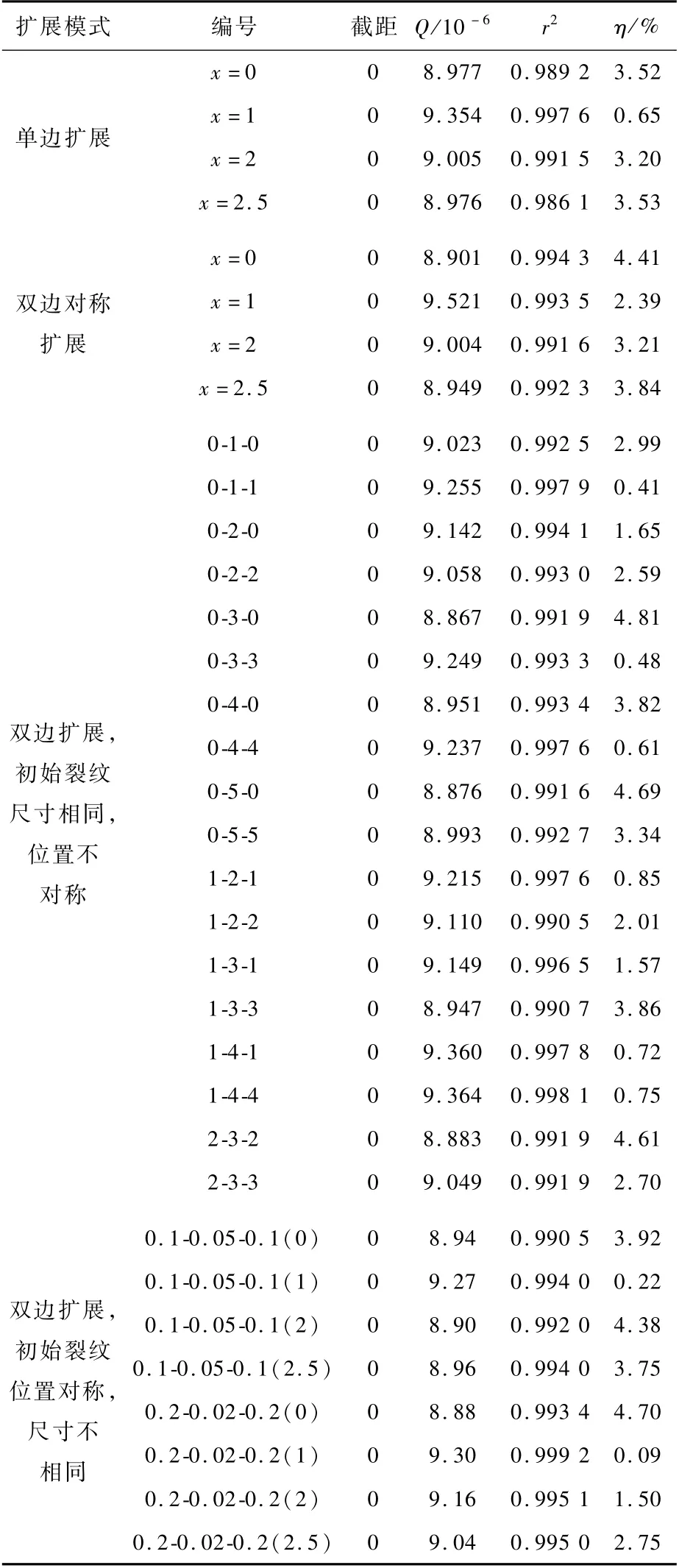
表4 da/dN-an/2数据处理结果Table 4 da/dN-an/2 data processing results
由表4可知,在a<0.88 mm 范围内,d a/d N-an/2数据线性度良好,有式(8)成立;Q与Q′在误差许可范围内,有式(9)成立,且Q的取值与初始裂纹位置、裂纹扩展方式(单边/双边扩展)无关。
3 耐久性试验验证
3.1 耐久性试验
耐久性试验采用中心圆孔平板试件,试件材料为7B04 T7451铝合金,取样方向L-S方向,根据试件孔径和宽度的不同分为3种,如表5所示,试件示意图如图4所示。各试验组应力比R=0.1,峰值应力及有效试件数如表5所示。

图4 试件尺寸示意图Fig.4 Schematic diagram of specimen size
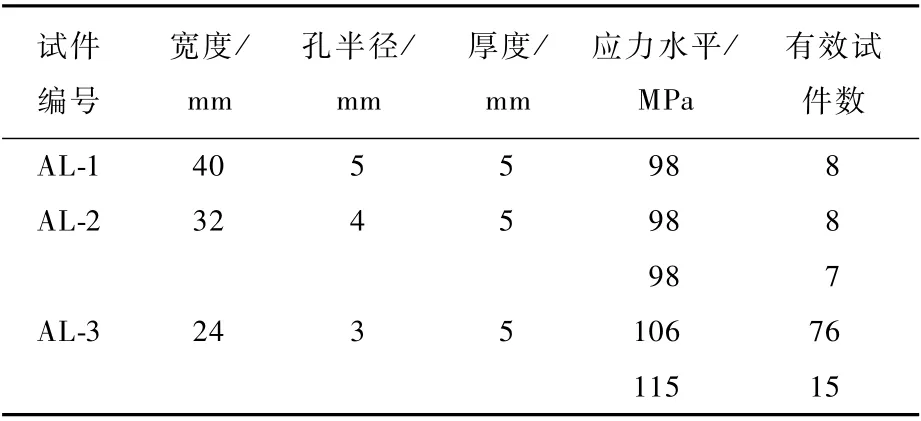
表5 试件尺寸及试验结果Table 5 Specimen size andexperimental results
疲劳试验在Instron 8801液压伺服疲劳试验机上进行,试件直接夹持在夹头上。试验在室温大气环境下进行,轴向加载,正弦波,加载频率5 Hz。为能通过断口判读获取裂纹前缘形状和扩展数据,参考文献[21],在等幅谱中定期插入标识载荷。试验后在工具显微镜下判读断口,获得(a,N)数据。
3.2 参数确定

对各试件a<au(au如表1所示)范围内的d a/d N-a1.566数据分别进行线性拟合,取截距为0,斜率即为对应的Qi(i为试件编号),如表6所示,其中r2为相关系数,试验组编号中括号内的数值为应力水平。由表6可知,在a<au范围内,各试件的d a/d N-a1.566数据线性度良好,有式(8)成立。
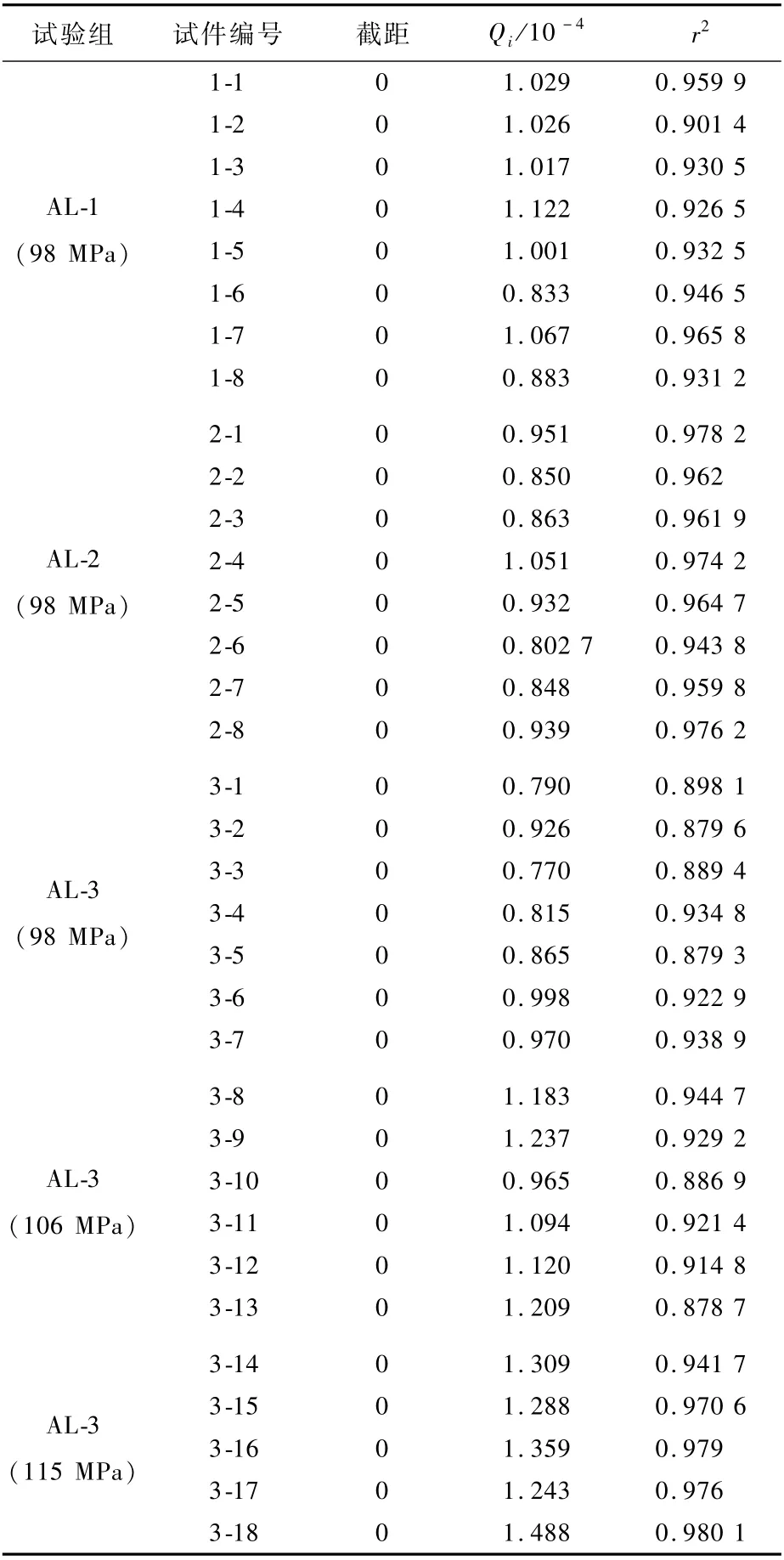
表6 各试件的da/dN-a1.566数据拟合结果Table 6 da/dN-a1.566 data fitting result of specimens
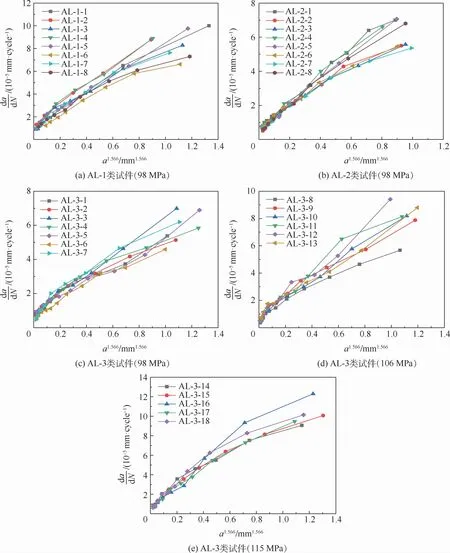
图5 各试验组的d a/d N-a1.566曲线Fig.5 d a/d N-a1.566 curves of experimental groups
由于材料力学特性的分散性,疲劳裂纹扩展速率参数C、n具有分散性,不能用某一试件的d a/d N-an/2数据来表征该种试件在某一应力水平下的裂纹扩展,须综合该应力水平下的所有d a/d N-an/2数据进行表征。假设同一类试件在给定应力水平下的Q服从对数正态分布,记Z=lg Q,则Z的概率密度函数为
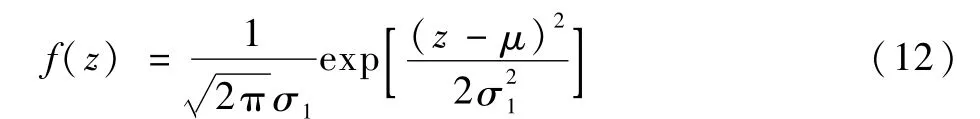
式中:μ和σ1分别为Z的期望和标准差。
则相关参数估计值为
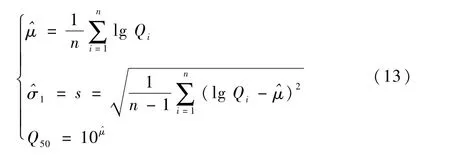
基于式(13)获得各试验组对应的Q50,如表7所示。基于7B04 T7451铝合金稳定裂纹扩展段的疲劳裂纹扩展速率参数[22],将参数C、n、σ、R和Y0代入式(9)计算Q′,并得到η,将Q′、η、au和Y0一并列入表7中。由表7可得,在a<au范围内,Q50与Q′在误差许可范围内,有式(9)成立。
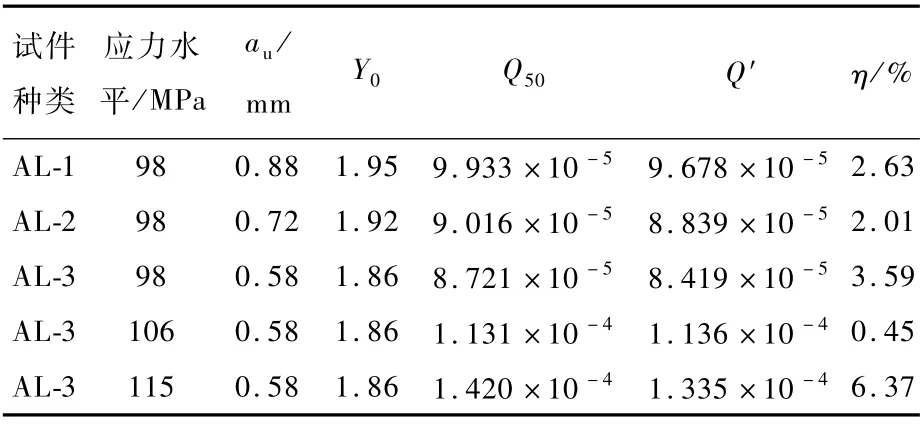
表7 da/dN-a1.566数据处理结果Table 7 da/dN-a1.566 data processing result
4 结 论
本文以受远场均匀拉伸载荷作用的含中心圆孔板为对象,基于裂纹扩展分析和耐久性试验结果分析,验证了耐久性相对小裂纹扩展速率公式,并给出了参数确定方法。结论如下:
1)裂纹扩展速率公式d a/d N=Qab可用于描述相对小裂纹扩展速率,该公式使用范围(裂纹长度上限)根据应力强度因子修正系数近似展开式中首项的误差确定。
2)等幅应力下的裂纹扩展速率参数