变体航行器动力学建模与仿真

颜奇民，胡俊华，陈国明，刘安，张强

（空军工程大学航空工程学院，西安 710038）

变体航行器是指在航行过程中能够改变自身结构特征以适应外界环境和任务需求的一类航行器，其涵盖范围十分广泛，包括变体水下航行器、变体飞机、跨介质航行器、变体航天器等，由于变体航行器可以实现不同构型间的切换，其相比固定构型航行器功能更加丰富、任务范围更广［1］。

变体航行器的动力学建模和仿真往往十分复杂，航行器变体过程中，自身的各项参数会发生变化，如变体飞行器的气动参数、变体水下航行器的水动参数，同时，航行器变体过程中自身结构的调整也会对航行器的运动状态产生影响；针对变体航行器的动力学建模问题，许来斌等［2］基于牛顿欧拉方程，推导了变体飞机运动方程并进行了俯仰和转向运动仿真；王志刚等［3］针对一种后掠变展长组合变形飞行器模型，采用多刚体理论建立了描述飞行器变形过程的动力学模型；Seigler等［4-6］建立了固定于飞机机身的机体坐标轴系，采用笛卡儿矢量描述机体各点的位置，推导了变体飞机的一般动态特性；陈伟和冯高鹏［7］将变体飞机视为一个质点系，得到了变体飞机的力方程和力矩方程；谭骏怡等［8］结合有限元思想和分析力学方法分别分析了刚性翼和柔性翼的动力学特性，并构建了变体飞行耦合动力学模型；上述研究分别建立了针对变体飞机的变体动力学模型，但是存在计算复杂、适用范围小等问题。

本文在陈伟和冯高鹏［7］的研究基础上，采用积分思想，将变体飞机视为由无数质点组成的质点系，建立固定于机体的机体坐标系，分析每个质点的运动，推导了变体航行器动力学扩展方程；对一种具有共形半环翼的变体航行器进行了不同变体速率下的纵向面内开环仿真，针对建立的动力学模型中部分附加力和附加力矩计算困难的问题，根据该航行器的已知变体规律，计算了不同时间节点航行器的静矩并拟合得到静矩的一阶和二阶导数，附加力矩中非静矩的未知项换算为包含静矩的二阶导数的已知项进行计算，简化了计算过程。

1 变体航行器动力学建模

1.1 坐标系建立

以航行器未变体时的质心作为原点建立机体坐标系O1x1y1z1，地面坐标系为O0x0y0z0，如图1所示［9］。

图1 坐标系建立［9］Fig.1 Coordinate system setup［9］

式中：sinγ，cosγ，sinϑ，cosϑ，sinψ，cosψ分别为航行器滚转角γ、俯仰角ϑ和偏航角ψ的正弦和余弦值。

1.2 变体航行器运动方程

将航行器视为由n个质点组成的整体，首先，在地面坐标系中描述航行器的n个质点的位置，表达式为

在此，引入运算符“～”表示向量元素组成的反对称矩阵，其规则为：若x＝xii+xjj+xkk（i，j，k表示沿标准坐标系3个坐标轴的单位矢量），则

式中：Ω ＝［ωxb，ωyb，ωzb］T为机体坐标系相对于地面坐标系的角速度在机体坐标系中的表示；ω为角速度矢量，ωxb、ωyb、ωzb分别为该矢量沿机体坐标系x轴、y轴、z轴的分量。

对式（2）两端求导得

式（21）即普通航行器的动力学方程，因此，本文得到的动力学方程（20）即变体航行器的动力学扩展方程，可以适用于发生任意可知形变的变体航行器，如变后掠航行器、折叠翼航行器、伸缩翼航行器等。

转动惯量张量I的具体表达式为［13］

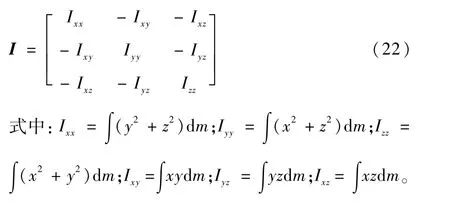
2 共形半环翼航行器变体描述

本文研究的共形半环翼航行器是一种具有共形半环翼布局的跨介质航行器，其空中构型和水下构型分别如图2（a）和图2（b）所示［14-15］。

图2 共形半环翼航行器构型［14-15］Fig.2 Configuration of conformal semi-ring wing vehicle［14-15］

该航行器构型主要针对水空跨越任务提出，航行器在水中航行时，共形半环翼收起，包裹于机体上，其构型与鱼雷相似，航行器冲出水面后，共形半环翼展开为空中构型，迅速加速获取升力起飞，当航行器准备再次入水时，机翼在空中收起，转换为水下构型，并减速俯冲入水。

共形半环翼包含2层翼面，其中，下层翼为刚性翼，上层翼为可弯曲的柔性翼，上、下翼面在翼梢端点处连接，航行器变体时，作动器控制下层翼转动，进而带动上层翼发生转动和弹性形变，其变体过程的翼型正视图如图3所示。

图3 共形半环翼航行器变体过程Fig.3 Process of variant of conformal semi-ring wing vehicle

由于航行器进行对称变体，为准确描述航行器变体情况，取航行器正向单侧剖面，如图4所示。

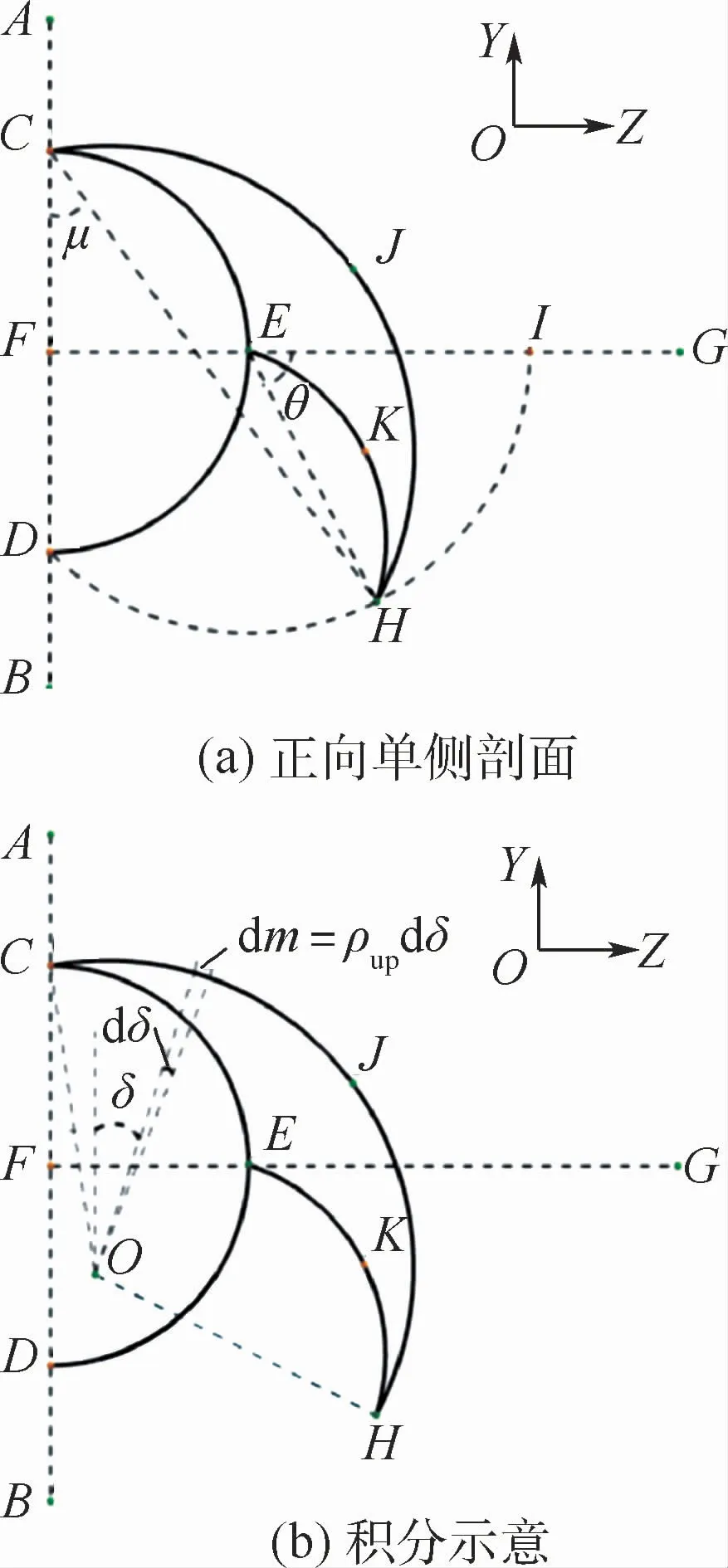
图4 航行器正向单侧剖面图Fig.4 Forward unilateral profile of vehicle

图4中，角θ和角μ分别用以描述下层翼和上层翼的转动角度，且μ的值与θ的值一一对应。

本文的仿真中，设计航行器以不同的变体速度在θ＝0和θ＝3π／8之间进行收回或展开，变体规律为

式中：˙ωθ为下层翼的角加速度，ωθ为下层翼的旋转角速度。

3 航行器变体气动参数

采用Fluent流体力学仿真软件对航行器的升力系数、阻力系数和俯仰力矩系数进行了解算，得到了航行器在不同攻角、不同变体角度的气动系数。根据仿真结果和研究分析，共形半环翼航行器的安全攻角范围为［-π／18，π／9］，因此，本节给出［-π／18，π／9］攻角范围和［0，3π／4］下层翼变体角度范围对应的气动参数（图中已将弧度折算为角度），如图5所示。

图5 航行器变体气动参数Fig.5 Aerodynamic parameters of vehicle in variant phase

4 附加力与附加力矩计算

航行器机翼变形对航行器运动的影响具体表现为由于变形产生的附加力F1～F4及力矩M1～M3，根据附加力和附加力矩表达式，计算附加力需要求得的物理量除基本的运动参数外，还包括静矩S及其一阶、二阶导数，以及附加力矩

本文航行器仅机翼发生变体，因此航行器静矩全部来源于机翼质心的变化，文中采取积分方法计算机翼产生的静矩，如图4（b）所示。

分别计算上、下层翼产生的静矩，可得

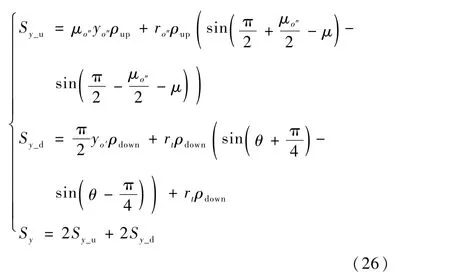
式中：Sy_u和Sy_d分别为上、下层翼产生的静矩；yo″和yo′分别为上、下层翼圆心的纵坐标；μo″、ro″、ρup分别为上层翼的圆心角、半径和单位弧度的质量；rt、ρdown分别为下层翼的半径和单位弧度的质量。根据航行器变体规律，这些参数均可求得。

本文在设定kθ后，可求取航行器变体总用时tw，以tw／20为步长，计算不同时刻的Sy，并利用MATLAB拟合功能［16］，快速求解S·y、S··y的近似值，本文航行器机翼由完全闭合至完全展开过程为例，其静矩及静矩的一阶、二阶导数变化情况如图6所示。

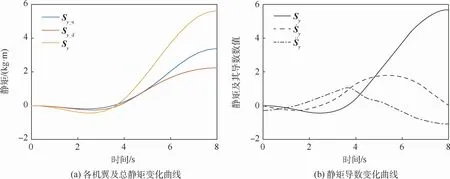
图6 静矩及其导数变化曲线Fig.6 Variation curve of static moment and its derivative

5 不同变体速率开环仿真分析

为研究开环配平状态下不同的航行器变体速度对航行器运动状态的影响，设定航行器的飞行速度为0.8 Ma，分别对航行器下层翼角度θ＝0和θ＝3π／8两种状态进行配平，得到两组配平状态［17］，分别记为A和B，其具体参数如表1所示。

令航行器以不同的变体速度在θ＝0和θ＝3π／8之间进行收回或展开，分别设置变体时间为8，4，2，1 s，仿真结果如图7和图8所示。

由图7和图8可知，在配平状态下，航行器机翼由θ＝0收回至θ＝3π／8状态，会导致航行器产生俯冲运动，速度增加，反之，航行器机翼展开会导致爬升运动，速度降低，同时，航行器变体速度越快，运动状态变化越剧烈。

图7 机翼收回仿真结果Fig.7 Simulation results of retracting wing

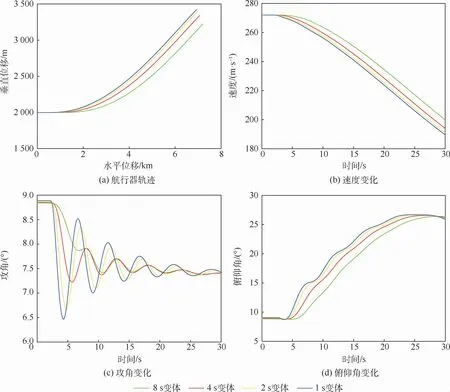
图8 机翼展开仿真结果Fig.8 Simulation results of unfolding wing

2种变体情况都会使航行器的攻角和俯仰角发生振荡。机翼收回时，攻角总体有所上升，俯仰角先上升，而后有下降趋势；机翼展开仿真中，总体趋势与收回仿真相反。这是因为航行器机翼在收回和展开过程中引起气动参数发生变化，在机翼收回过程中，航行器升力、阻力系数和负向俯仰力矩均减小，导致航行器产生俯冲，速度增大，俯仰角增大，从而导致航行器攻角迅速增大，由于航行器具有纵向静稳定性，攻角的增大会引起负向俯仰力矩增加，航行器俯仰角和攻角减小，且在纵向静稳定性的影响下，随后航行器的攻角和俯仰角会产生逐步减小的振荡。

航行器机翼收回过程和展开过程中附加力和附加力矩变化方向相反而趋势相似，因此只给出航行器机翼收回过程中的附加力和附加力矩的变化情况，如图9所示。

图9 附加力与附加力矩变化曲线Fig.9 Variation curve of additional forces and additional moments

基于本文航行器的结构，其变体产生的静矩均沿y1轴，根据附加力与附加力矩的表达式，在航行器俯仰运动中，F1与F4沿y1轴方向，F2与F3沿x1轴方向，M1、M2、M3均沿z1轴方向，因此直接给出各个附加力与附加力矩沿相应轴向的值。

由图9可得，配平状态下航行器进行变体时，变体速度越快，产生的附加力与附加力矩越大。在本次仿真中，F4的值远大于其他附加力，这是因为该仿真中航行器的角速度和角加速度均较小，导致F1～F3较小，F4为航行器静矩的二阶导，可以理解为机翼变体过程中机翼上质点加速对机身产生的反作用力。

附加力矩中，M3的值远大于其他附加力矩，这是由于航行器的角速度、加速度较小，导致M1较小，同时，本文航行器变体过程中惯量矩阵的变化率很低，导致M2的值很小，而M3可以理解为机翼变体过程中的机翼上质点加、减速产生反作用力偏离质心所产生的力矩，变体越快，产生的M3力矩越大。

6 结 论

本文建立了变体航行器的动力学拓展方程，针对变体规律已知的共形半环翼航行器，对不同时刻的静矩及转动惯量进行拟合和求导，求得其变体附加力和附加力矩，该方法也可以适用于其他具有已知变体规律的变体航行器的动力学建模，包括变体飞行器、变体航天器等。

共形半环翼航行器变体飞行的开环仿真结果表明，航行器变体产生的附加力和附加力矩大小与变体速率正相关，其中，由静矩变化引起的F4和M3影响最大；由于本文航行器机翼在整机中占比小，附加力和附加力矩远小于气动力，引起航行器运动状态变化的主要因素仍然是变体导致的气动参数的变化；对于大幅度变体的航行器，则必须考虑附加力和附加力矩对运动的影响。