基于合作博弈的个人综合所得税地区分配方式研究
2022-01-15聂海峰
一、引 言
个人综合所得由个人的工资薪金、劳务报酬、稿酬和特许权使用费所得四项所得构成。从2019年开始,综合所得的税收按年征收,纳税人在第二年将上一年度全部综合所得进行费用扣除、专项扣除、专项附加扣除、合理的捐赠扣除和法律规定的其他扣除后,将应纳税所得对应综合所得的七级累进税率向税务部门进行申报纳税和汇算清缴。综合所得征税的方式,使纳税人来自不同地区的综合所得统一纳税,改变了以往分类所得在来源地纳税的方式。个人所得税的征管方式,从分类所得的代扣代缴转变为预扣预缴和申报汇算清缴的方式。具有多处综合所得来源的个人,需要向主管税务机关申报纳税进行汇算清缴:如果预扣预缴的税额比应纳税额少,个人需要补税;反之,如果预扣预缴的税额比应纳税额多,主管税务部门要对纳税人进行退税。由于个人收入来源于多处地区,相比原来分类所得征收,综合征收产生了税务部门退税分摊和税收地区间分配的两个新问题:
首先是主管部门对纳税人的退税如何在不同收入来源地分摊的问题。纳税人由于工作地点变动、收入的地区分布差异等原因导致纳税申报主管税务地和主要收入来源地不一致,负责纳税人办理汇算清缴退税的地区可能并没有获得纳税人预扣预缴的税收。法律规定由主管税务部门先行办理退税,但是退税和预扣预缴的差异会影响地区之间税收收入的分布。这导致了汇算清缴主管地和个人收入来源地的税收利益冲突。
痊愈为NIHSS评分减少≥90%,脑电图正常;显效为90%>NIHSS评分减少≥50%,脑电图显著改善;有效为49%>NIHSS分恢复≥15%,脑电图有所好转;无效为以上指标均未满足。
其次是各收入来源地如何分享个人的税收。在分类征收时,个人在每个地区获得收入时代扣代缴的税收直接归属于收入来源地,各地的收入彼此无关,收入来源地可以获得相应的税收。在综合所得税制下,在收入来源地只是预扣预缴,所有地区一年内的综合所得合并在一起计算纳税人的最后应纳税额。由于累进税率和共享纳税人的扣除,各地的收入互相影响,共同决定纳税人的综合所得应纳税额。预扣预缴的税率和纳税人综合所得的最后适用税率并不一致,如果纳税人年度汇算申报时补税,需要解决相应税收如何根据个人来自各地的综合所得进行分配的问题。
对这两个问题,当前的解决方法是由汇算清缴地负担全部退税,也由汇算清缴地获得全部汇算清缴时补缴的税收。当前分配方案下,预扣预缴地区获得预扣预缴的税收,而汇算清缴地区获得全部收入的税收,并对其他地区已经预扣预缴的税收提供可退税的抵免。这使得汇算清缴地所得适用个人综合所得税率,而其他地区的所得只适用预扣预缴税率。当个人全年综合所得最高边际税率低于其他地区预扣预缴的税率时,汇算清缴地负责退税,就产生了预扣预缴地和汇算清缴地之间的税负输出问题。因而,现行分配方案没有考虑各地收入在税收创造中的公平地位,存在来源不同地区所得适用税率差异和地区间税负输出问题。
退税分摊问题和地区税收分配问题可以分别单独解决,也可以同时一起解决。如果确定了个人综合所得税在地区之间分配的方式,退税分摊的问题可以看作是地区税收分配的子问题,两个问题按照统一的方式进行解决。本文从合作博弈解的分配角度,提出了基于原则的地区之间个人综合所得税的分配方式,为完善综合所得税制提出了解决和改进思路。
虽然个人所得税地区间分配问题刚刚出现,规模和人数都在初步阶段,但是随着直接税在我国税收收入比重的上升,本文研究的意义会日渐重要。在营改增完成之后,个人所得税已经成为地方政府财政收入的重要来源,如何分配个人所得税收入对地方提供公共服务能力具有重要影响。个人所得税已经是我国税收收入中重要的税种,2018年在全国税收收入中占第3位,在地方税收收入中占第5位。个人所得税是中央和地方分享税,中央和地方按照60比40分享当地的税收收入。在分类征收时,来自各地区的收入由地方和中央直接交涉,各地区之间互不干涉。但在综合所得征收后,纳税人来自各地的综合所得共同决定最后应纳税额。个人综合所得税地区分配问题,涉及到财税体制的地区税收分享问题,是我国建设现代财税治理体制的重要问题。
第四,配套完整、齐全的法律法规。目前面临的实际情况是,对于重组整合,相应的法律法规条款不完善。某些具体的条款不够全面完整。对于某些情况取而代之的是行政指挥命令的方式。这种也很容易影响权利寻租,金钱交易等情况。进而阻碍企业的重组整合进度。影响进度和效率。
在购置实验教学仪器设备之前,应该有详细的购置计划,尽量避免购买重复的实验器材,合理地利用实验建设经费,在列采购清单前一定进行以下几项:首先,查看现有的实验设备是否满足实验需求,其次,统计实验室提出的设备购置申请,最后请专家按照教学大纲合理地对采购清单进行审核修改,交到财务部门进行审核,审核通过后给予采购。
在我国的税制发展过程中,其他税种也有涉及类似的地区之间税收分配问题。但是以下三个个人所得税的特征决定了政府需要根据个人所得税的特点制定新的办法:
用不同浓度的 GSK126 (0、2、5、10、15、20、30、40、50、80 μmol/L) 干预 ONFH 组 MSCs,以确定GSK126最适浓度。然后以最适浓度干预细胞,观察24、48、72 h后细胞增殖情况。调整细胞悬液浓度为2×104/ml,接种于96孔板,各组10孔。培养一定时间后,每孔加入MTT溶液20 μl,37℃孵育4 h后去除上清液,每孔加入150 μl DMSO,振荡10 min,酶联免疫检测仪测定各孔吸光值(波长490 nm)。
第一,个人所得税纳税人数规模大。增值税和企业所得税主要涉及企业行为,而个人所得税涉及个人。根据公开报道,个人所得税的纳税人有2.5亿人
,需要纳税申报的人数规模可能达到8000万
。根据第四次全国经济普查公报,2018年末全国共有从事第二产业和第三产业活动的法人单位2178.9万个
。个人纳税人的数量超过了企业纳税人。
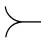
值分配作为合作博弈的解最早由Tijs(1981)提出
。在一个合作博弈(
,
)中,
=
(
)-
(
{
})是地区
在博弈中能得到的收益的支付上限,如果地区
的收益高于这个上限,其他
-1个地区就不愿意和地区
组成联盟来分配收益。因而
维向量
=(
,
,…,
)称为博弈的理想值向量。在综合所得税地区分配中,
表示参与人地区在形成联盟时在最后一个加入联盟的边际收益。由于综合所得税地区分配博弈是凸博弈,对于任意
⊆
⊆
{
},都有
(
∪{
})-
(
)≤
(
∪{
})-
(
)。在形成大联盟的过程中,最后一个加入的边际收益大于其他位置加入时的边际收益
。由于累进税率,这是地区
的综合所得可以适用个人可以达到的最高边际税率时带来的税收增加。对于任意地区
和任意包含
的联盟
,如果其他每个参与人都得到理想值支付,形成联盟后的价值对于参与人
的剩余值为:
第三,个人收入明确。个人因任职、受雇、提供劳务、创作或者转让特许权获得所得,通常是市场公平交易。而企业总分机构之间的交易存在内部转让定价,因而个体的收入具有客观公平性,预扣预缴税务部门具有可靠的记录,可以作为分配税收的基础。
个人所得税的纳税人数目规模大、地区流动频繁和收入明确的特点,使得通过固定公式根据纳税人来自各地的综合所得在地区之间进行公平合理分配,具有公平、公开和公正的特点。通过固定公式分配,分配方式在地区之间透明,便于各地区合作,维护各地区的税收利益。在纳税遵从方面,也便于纳税人理解执行,不影响纳税人就业选择和纳税遵从。聂海峰和刘怡(2020)建立了一个合作博弈模型,讨论了博弈的Shapley值作为地区间税收分配办法的性质,将地区间税收分配问题转化成了文献中的破产问题,提出应用比例法在地区间分配税收:各地区根据来自当地的综合所得占纳税人全部综合所得的比例来分享纳税人应纳税额
。但是比例法分配没有考虑到各地区的收入在纳税人税收创造过程中的作用。
合作博弈是描述多个参与人之间存在约束性协议时,如何在参与人之间公平合理分配彼此共同合作的收益的理论
。在个人综合所得税地区分配问题方面,收入来源的各地区彼此间存在合作和冲突,正好适应合作博弈分析的情景:每个地区都对来自当地的收入有税收征管权,综合所得的累进税率使得个人的收入越多时适用的税率越高。税收分配要保证各地对来自当地税收的基本权利,也要保证分享所有地区一起合作的收益。一旦中央政府选定分配方式,参与地区存在执行协议的约束性。作为地区间税收分配方式,至少满足三个性质:首先是效率性,即所有地区分配相应的全部税收,并且各地区之间不能存在交叉补贴;第二是对称性,即两个具有相同收入的地区应当分配相同的收入;第三是单调性,即综合所得多的地区分配的税收应当不低于综合所得少的地区分配的税收。合作博弈的多种解都满足上述三个性质。
本文的贡献是考虑了合作博弈的多种解,丰富了个人所得税地区间分配问题的解决方案。和Shapley值一样,核仁(Nucleolus)和
值作为合作博弈的解也满足效率性、对称性和单调性的性质。在合作博弈中,对于“公平”的不同解释导致不同的合理解。在Shapley值分配中,每个参与人得到了在合作中的边际贡献。核仁反映了分配方案中不同地区组合的所得和他们自身可以创造税收的差异的最小化,是福利经济学中罗尔斯原则——最大化境遇最差人福利的应用。
值反映参与人在合作博弈中理想值和最小权利值之间的折中。最小权利值反映了参与人参与博弈时至少应当获得的最低收益,而理想值是他参与合作时能获得的最大可能收益。
值分配中,每个参与人保证获得他的最小权利值之后,剩余的合作收益按照每个人未满足的理想值成比例分配。
(1a)赵先生在两处任职受雇地获得工薪收入,赵先生选择A地为主管税务机关所在地。因此,赵先生的专项附加扣除在A地每月工薪所得领取时使用。因而在A地,赵先生的工薪应纳税所得为
=4*12=48万元。由于费用扣除=0
5*12=6万元,专项扣除=1*12=12万元,专项附加扣除=2
4+2
4=4
8万元,赵先生在A地预扣预缴时的全年应纳税所得=48-6-4
8-12=25
2万元。在A地被全年累计预扣预缴的税款为
=0
2*25
2-1
692=3
348万元。
合作博弈的解作为公平合理的分配方式,已经被广泛应用:比如美国田纳西流域建设成本分摊方法和合作博弈中各种解的关系
,合作博弈在保险研究中的应用
,以及合作博弈在中国机场起降费规制改革中的应用
。鉴于Curiel、Maschler和Tijs(1987)提出在破产博弈中利用
值解决破产后债务清偿问题
,本文尝试将
值分配用于解决地区个人所得税的分配问题。
本文余下内容安排如下:第二部分首先对地区税收分配问题构建合作博弈模型,第三部分介绍核仁和
值的性质,将其与Shapley值分配进行对比,并用案例比较分配结果。最后是全文的总结,讨论影响个人所得税地区间分配方法选择的因素。
早在2008 年西门子公司因违反《反海外腐败法》被处罚金16 亿美元,成为全球企业合规发展的一个里程碑事件。从那以后,强化合规管理、防范合规风险已经成为越来越多企业管理创新的重要内容。统计数据显示,自2014 年初以来,已公开宣布115 名国有集团公司的决策层高管因贪污而受到调查,一些央企的主要负责人被调查或处罚。
二、个人综合所得税地区分配问题
(一)个人综合所得税汇算清缴
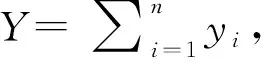
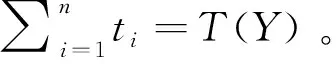
(二)合作博弈分析
合作博弈和传统的非合作博弈不同。合作博弈关注合作利益分配方式的研究,而非合作博弈关注参与人的利益最大化的均衡策略的确定。非合作博弈关注自利参与人的选择的激励相容性,而合作博弈关注收益分配方法的公平、效率和个人理性。
从合作博弈角度,个人综合所得税地区分配问题对应着
个地区之间合作利益分配问题。Von Neumann和Morgenstern(1953)最早提出了联盟形式的合作博弈
。带转移效用的合作博弈由二元组(
,
)表示,这里
={1,2,…,
}表示参与人集合,
是从集合
的所有子集到实数集合的映射,
:2
→
。对于任意参与者的联盟
⊆
,
(
)给出该联盟合作的价值。在税收地区分配问题中,参与人是个人获得综合所得的地区,
(
)=
(∑
∈
)等于所有联盟
中的地区联合起来可以从该个体获得的税收收入。当个人收入来源于多个地区时,地区之间的信息共享才能使得在个人申报纳税时实现综合所得税的良好征管。
(∑
∈
)反映了联盟地区之间信息共享、联盟外的收入信息不被联盟分享的极端假设。对于空集Ø,有
(Ø)=0。
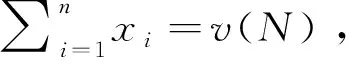
确定合作博弈的解就是寻找恰当分配方案,将合作的收益在参与人之间分配。常用的一个分配原则是激励原则:由于各个成员之间可以组成联盟,每个联盟分配的总和不应当低于他们自身组成联盟时的收益。否则,联盟成员就没有参加大联盟收益分配的激励。这意味着对于任意的联盟
,都要有∑
∈
≥
(
)。满足激励原则的分配方案称为博弈的核心(
)。

对于凸博弈,核心总是存在但不唯一,因而不能给出单一值的合理分配方案。在文献中,广为使用的单一值分配方案是Shapley值、核仁和τ值。作为合作博弈的解概念,可以给出可行的合理分配方案。
三、地区税收分配合作博弈的解比较
(一)Shapley值分配
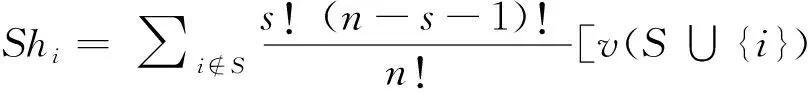
(二)核仁分配
在第二年3月1日至6月30日内,赵先生由于从两处以上取得综合所得,且综合所得年收入额减除专项扣除后的余额超过6万元,赵先生到主管税务机关A地的税务部门办理个人申报进行个人汇算清缴。
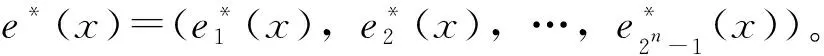
2.2 两组患者冠状动脉造影、介入治疗及术后情况比较 两组患者冠状动脉造影结果提示“罪犯”血管累及回旋支和右冠的比例、术前TIMI血流、术后严重出血、急性/亚急性支架内血栓形成、延迟支架植入比例等方面差异无统计学意义(P>0.05);两组“罪犯”血管累及左主干和前降支的比例、>70%狭窄的冠脉病变数、术中发生无复流、冠脉支架术后TIMI血流和完全血运重建的比例等方面,差异有统计学意义(P<0.05)。见表2。
(三)τ值分配
第二,个人流动性高于企业。企业登记注册和经营地相对固定,企业的迁移成本较高。随着户籍制度完善,教育、就业以及医疗、养老、住房保障等领域的配套政策加快完善,人口就业地区之间流动的频率和规模远远高于企业。根据《中国流动人口发展报告2018》推算,2017年全国流动人口总量为2.445亿人。
(
,
)=
(
)-∑
∈{}
(1)
参与人
的最小权利值(Minimal Right Value)定义为
=max
;∈
(
,
),表示参与人
可以通过形成一个联盟,支付联盟中其他参与人可以得到的上限支付后,确保自己得到的支付。如果地区之间可以自由结合成各种联盟时,这是地区
可以确保得到的最小支付。因而
维向量
=(
,
,…,
)称为合作博弈的下值向量。
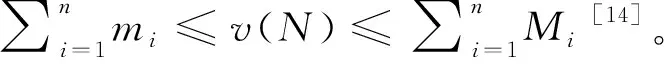
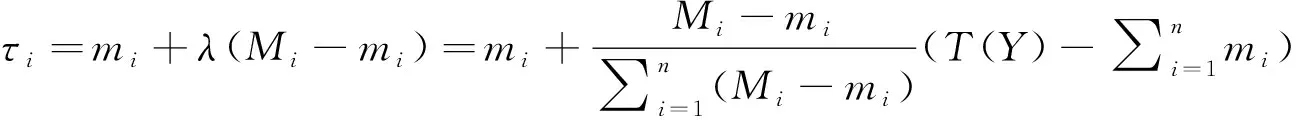
(2)
值作为博弈中参与人的理想值和下值的折中,也具有良好的性质。首先它满足效率性,在所有参与人之间分配合作的总收益;其次满足对称性,如果两个地区具有相同的综合所得,
值会分配相同的税收;再次满足单调性,如果
≥
,则
≥
,即来自地区
的综合所得大于来自地区
的综合所得,那么分配给地区
的税收不低于分配给地区
的税收;最后,如果每个地区单独的综合所得的税收为零(
=0),那么所有地区分配的税收和他们的理想值
成比例。因而,
值的分配类似一种调整比例分配办法,先分配给每个地区的下值对应的税收,然后将未分配的税收,根据去掉已经分配的税收后的理想值税收按照比例进行分配。当成比例分配时,
值分配是根据理想税收收入的比例分配的,而不是根据该地区的综合所得进行分配,更好反映了收入创造税收的功能。
重组改构人肿瘤坏死因子对比顺铂胸腔灌注治疗恶性胸腔积液疗效与安全性的系统评价 ……………… 郭奇遇等(6):839
(四)三种分配方案比较
Shapley值、核仁和
值分配都满足效率性、对称性和单调性的性质。这三种分配结果有时相同,但是相对来说,
值的计算步骤最简单,而Shapley值分配和核仁分配的计算过程都比较复杂。
1.3.1 小鼠LLC细胞培养及肺癌移植瘤模型建立 收集对数生长期LLC细胞,制成1×106个/mL的单细胞悬液;0.2 mL/只,皮下注射入30只C57/BL6小鼠左侧腋下,观察、记录LLC小鼠生长及成瘤情况。
对于一般的情形,这三种分配方法分配的结果不同。Shapley值分配和核仁分配结果总是在博弈的核心中。如果参与分配的地区超过4个,
值的分配可能不在博弈的核心中
。虽然在给定收入时,Shapley值分配和核仁分配都满足单调性,但是核仁分配不满足联盟单调性(Coalition Monotonicity)和强单调性(Strong Monotonicity)。联盟单调性是指两个联盟博弈(
,
)和(
,
),存在一个联盟
满足
(
)>
(
),但是对于任意
≠
,都有
(
)=
(
),那么对于任意
∈
,
(
,
)
>
(
,
)
。这里
是博弈的解,表示如果博弈中某个联盟的收益增加了而其他联盟收益不变,那么这个联盟中包含的参与人分配的收益也要增加。强单调性是指如果对于任意
,
∈
,都有
(
)>
(
),那么
(
,
)
>
(
,
)
。强单调性意味着如果包含参与人
的所有联盟的收益增加了,那么参与人
分配的收益也要增加。Megiddo(1974)通过构造例子表明核仁分配不满足联盟单调性,因而也不满足强单调性
。在地区税收分配中,分配方案满足强单调性意味着如果其他地区的综合所得不变,来自一个地区的综合所得增加了,那么这个地区在收入增加后分配税收不低于收入增加前分配得到的税收。由于核仁分配不满足强单调性,这对核仁的应用是一个不利之处。
在计算复杂性方面,
值的计算最为简单,只需要计算2
+1个联盟的收益;而Shapley值分配和核仁分配都需要计算所有2
个联盟的收益,计算的工作量较大。因而,从计算简单性角度考虑,
值分配方法也是一种具有良好应用前景的选择。
杨宗祥曾经说过“企业家应以人为本来管理企业,董事长及高管、班组长不可能天天去当操作工、开挖机,这些行业的员工很辛苦,企业家要将心比心,解决员工后顾之忧,企业才能获得长远的发展”。为员工购买社会保险,遭遇金融危机工资不降,开发物业成本价基础上还发放补助金保证职工有房住,员工的工会活动经费总是第一时间达到,外加中午免费的午餐。公司各项福利水准在安宁当地也算上乘,绝大多数员工能安心本职工作,公司还为职工新建500套经济适用房,3000多名职工安心本职作业,多年来企业人员流失率始终保持在5%以下。
(五)案例分析
这里考虑一个收入来源于多地的地区税收分配案例。赵先生有2个子女,都在中小学读书,妻子未工作。他没有再接受继续教育,首套住房的贷款已经结清。赵先生为独子,父母双方健在,都超过了60岁。家人都健康,未有疾病。因而,在6项个税专项附加扣除方面,赵先生只适用子女教育和赡养老人两项,其中子女教育2
4万元
年,赡养老人2
4万元
年。
(a)赵先生在甲省A地任职,每月工资收入4万元,三险一金个人部分需缴纳1万元。
(b)因工作关系,公司派赵先生兼任甲省B地公司经理,在该公司每月工资收入2万元,三险一金个人部分缴纳0
5万元。
(c)赵先生6月被邀请赴乙省C地讲学一周,当地主办单位支付赵先生劳务报酬10万元。
(d)赵先生10月的一部书稿被丙省D地出版社出版,出版方支付稿酬5
7142万元。
(e)11月份,赵先生早年一部剧本的电影改编版权转让给丙省E地的一家影视公司,对方支付转让费6万元。
1
代扣代缴阶段
以上为赵先生全年收入,下面分别计算赵先生在各地取得收入时的代扣代缴情况和第二年个人申报纳税汇缴清算情况。
(1b)在B地,赵先生工薪应纳税所得
=2*12=24万元,预扣预缴时费用扣除和专项扣除都为6万元。在B地预扣预缴时全年应纳税所得=24-6-6=12万元。在B地被全年累计预扣预缴的税款为
=0
1*12-0
252=0
948万元。
本文的另一个贡献是提出了更具可行性的分配方式。相比于Shapley值和核仁分配,
值分配的计算公式较简单,在实践中更便于应用。
值也扩展了比例法。在比例法中,每个地区分配税收与来自该地的综合所得成比例;在
值分配中,每个地区保证了单独的贡献之后,分配的税收和来自当地的综合所得能创造的最大税收成比例。
值分配可以看作是一种调整后的比例分配。与按照综合所得比例法分配相比,
值考虑了各地区收入在税收创造过程中的作用,分配的比例因素是每个地区未满足的理想税收收入。
海水中悬浮物颗粒对光的选择性吸收是线性衰减系数不稳定的主要原因。在清澈的海域,除了蓝光的吸收和散射对光的衰减基本相等外,其他颜色的光衰减基本上是因为海水的吸收。在悬浮物比较多的海域,光的衰减则大部分来源于光的散射。而光在传播时产生的荧光散射和拉曼散射则包括了吸收和受激辐射两个基本过程。一般情况下,吸收作用造成的光量的衰减约占光源的40%,而其大部分原因是来源于光的散射作用。
(1c)扣除20
的费用后,赵先生来自C地的劳务报酬收入额
=(1-0
2)*10=8万元。在C地预扣预缴的税款为
=0
4*8-0
7=2
5万元。
干线公路项目施工过程中的质量安全风险管理问题探析………………………………………………………… 李梅(4-229)
(1d)来自D地的收入为稿酬所得,因而在D地的应纳税所得
=(1-0
2)*0
7*5
7142=3
2万元。按照20
的比例预扣率,在D地预扣预缴的税款为
=0
2*3
2=0
64万元
(1e)来自E地的收入为特许权使用费所得,在E地的应纳税所得
=(1-0
2)*6=4
8万元。按照20
的比例预扣率,在E地预扣预缴的税款为
=0
2*4
8=0
96万元
2.个人汇算清缴阶段
核仁是由Schmeidler(1969)提出的合作博弈的分配解
。Shapley值分配侧重考虑参与人在形成联盟时的边际贡献,而核仁强调分配的公平性,可以看作是从公平角度最大化最小分配方案差异的结果。Inarra、Serrano和Shimomura(2019)是对核仁研究的最新全面综述
。
赵先生的全年税前收入=48+24+10+5.7142+6=93.7142万元。费用扣除为6万元,两处取得工薪所得的专项扣除=12+6=18万元,6项专项附加扣除=4.8万元。扣除劳务报酬、稿酬所得和特许权使用费所得的费用后,赵先生综合所得收入额Y=48+24+8+3.2+4.8=88万元。因而,全年综合所得应纳税所得=88-6-18-4.8=59.2万元。根据对应的边际税率和速算扣除数,应纳税额T(Y)=0.3*59.2-5.292=12.468万元。
赵先生被预扣预缴的税收总额=3.348+0.948+2.5+0.64+0.96=8.396万元。因而,赵先生需要向A地主管税务机关补缴税款12.468-8.396=4.072万元。赵先生税前收入的个人所得税负担率=12.468/93.7142*100%=13.3%。
3.综合所得税地区分配阶段
赵先生全年综合所得收入额88万元来自5个地区,共享赵先生的费用扣除、专项扣除和专项附加扣除之后按照七级累进税率表创造了12.468万元的税收。在地区之间的税收分配,就是按照前文提到的合作博弈的分配方法分配赵先生的税收。然后根据分配的税收,其他4个地区和A地的主管税务机关进行汇算清缴。表1中列出了按照Shapley值、核仁值和
值分配的地区税收。相应分配的税收和当地已经预扣预缴的税收的差额就是与A地汇算清缴的数额。
从表1中列出的税收分配方案可以看到,如果不进行税收地区间分配,来自B地的收入高过了C地,但是预扣的税收低于C地。在汇算清缴阶段,补缴的税收将都归属与A地。B地的税收利益受到较大的影响。
一直以来,无论是市场营销学理论界还是教科书,都把市场营销分为传统和现代两大观念,作为市场营销学的经典理论被广泛应用。

在不同分配方案中,来自A地的应纳税所得最高,A地分配的税收也最多;来自D地的应纳税所得最低,相应分配的税收就最少。三种分配方法中,Shapley值方法分配给A地6.83万元,核仁方法分配给A地区6.638万元,而
值方法分配给A地区6.768万元。在给D地的税收分配中,核仁方法分配了0.48万元,Shapley值方法分配了0.464万元,
值方法分配了0.469万元。因而,Shapley值强调边际贡献,对来源应纳税所得最高的地区分配的税收较大,而核仁方法对应纳税所得较小的地区分配的税收相对Shapley值方法有所调整。
除了A地之外,其他四个地区的应纳税所得都小于个体的扣除合计,如果单独计算应纳税收等于0,四个地区的τ值分配的税收成比例。如果按照应纳税所得的比例分配,A地分配的税收将是B地的2倍,但是按照
值分配时,A地分配的税收高于B地的2倍,反映了在累进税率下A地创造税收的能力更高。因而,
值分配也优于按照应纳税所得比例分配。
四、总 结
个人综合所得税制是当前税制改革的新生事物,跨地区个人所得税分配也是一个新的现象。具有跨地区综合所得的纳税人的数目,所得规模和相应税收的规模都需要新的统计。因而,对于跨地区的个人所得税退税和地区分配问题,主管部门需要进行如下决策:第一,是否由主管税务机关负担所有退税;第二,是否在地区之间分配个人跨地区所得个人综合所得税;第三,如果分配,采用哪种原则在地区之间分配个人综合所得税。对于前两个问题,由于目前个人所得税比例较低,综合所得税制刚刚建立,采用过渡的办法,由主管税务机关负担所有退税,不在地区之间分配跨地区个人综合所得税。但是,随着全国劳动力市场统一,劳动力普遍自由流动,个人所得税占税收收入比重增加,跨地区所得成为普遍现象,维护地区间财政收益将成为重要的问题。本文分析讨论的各种分配方法,对未来的政策设计提供了参考指导,帮助政府未雨绸缪,提前谋划。
合作博弈的解对应的分配方法,为个人综合所得税在地区之间分配提供了选择方案,保证了各地区的收入得到公平的对待,并且具有明确可以执行的公式,具有透明性的优点。本文比较了合作博弈中广泛使用的Shapley值、核仁和
值三种博弈解对应的分配方案。这三种解给出的分配方式都满足良好的性质:效率性、对称性和单调性。但是核仁不满足联盟单调性,会导致来自一个地区的收入增加后分配的税收减少的情况。因而,Shapley值和
值作为地区间分配综合所得税的可行方案具有良好的性质。当个人收入来源地区较多时,Shapley值计算量比较大,在实际应用中较复杂;而
值分配的计算公式简单,结合了比例分配法的优点,具有容易使用和推广的潜力。
当然,多元合作英译模式仅是一种宏观的指导思想,要想做好“花儿”外译还需要提出具体的英译策略与方法。“花儿”是一种典型的民间口头传承诗歌,与传统诗歌有着极大的差异,不能简单套用译介传统诗歌的方法,必须另辟蹊径。对民俗学的口头程式理论和表演理论进行跨学科的阐发,可为“花儿”的英译研究提供新视角、新方法。
在具体实践中,除了效率、公平、单调和简明计算的特征之外,影响分配方法选择的另一个因素是收入影响规模。本文的进一步研究方向,就是利用具体的税收统计数据比较各种分配方法对地区之间税收收入分布的影响。
[1] 聂海峰, 刘怡. 个人所得税地区间汇算清缴方法研究[J]. 财政研究, 2020, (5): 90-102.
[2] Bezalel P., Sudhölter P. Introduction to the Theory of Cooperative Games[M]. Berlin Heidelberg: Springer, 2007.
[3] Straffin P., Heaney J. P. Game Theory and the Tennessee Valley Authority[J]. International Journal of Game Theory, 1981, (1): 35-43.
[4] Lemaire J. Cooperative Game Theory and Its Insurance Applications[J]. Journal of the International Actuarial Association, 1991, 21(1): 17-40.
[5] 董保民, 郭桂霞. 机场博弈与中国起降费规制改革: 一个合作博弈论评价[J]. 经济学(季刊), 2006, (3): 1235-1252.
[6] Curiel I., Maschler M., Tijs S. H. Bankruptcy Games[J]. Zeitschrift für Operations Research, 1987, (5): 143-159.
[7] Von Neumann J., Morgenstern O. Theory of Games and Economic Behavior[M]. Third Edition. New York: Princeton University Press, 1953.
[8] Shapley L. Cores of Convex Games[J]. International Journal of Game Theory, 1971, (1): 11-26.
[9] Shapley L. A Value for N-person Games[C]∥ Kuhn H. W., Tucker A. W. (Eds.). Contributions to the Theory of Games II. Princeton: Princeton University Press, 1953: 307-317.
[10] Schmeidler D. The Nucleolus of a Characteristic Function Game[J]. SIAM Journal on Applied Mathematics, 1969, (6): 1163-1170.
[11] Inarra E., Serrano R., Shimomura K. I. The Nucleolus, the Kernel, and the Bargaining Set: An Update[J]. Revue Economique, 2019, (2): 225-266.
[12] 谭春桥, 张强. 合作对策理论及应用[M]. 北京: 科学出版社, 2011.
[13] Tijs S. H. Bounds for the Core and the
-value[C]∥ Moeschlin O., Pallaschke D. (Eds.). Game Theory and Mathematical Economics. Cie: North-Holland Publishing Company. 1981: 123-132.
[14] Tijs S. H., Lipperts F. A. S. The Hypercube and the Core Cover of N-person Cooperative Games[J]. Cahiers du Centre d’études de Recherche Opérationnelle, 1982, (1): 27-37.
[15] Tijs S., Otten G. Compromise Values in Cooperative Game Theory[J]. Top, 1993, (1): 1-36.
[16] Megiddo N. On the Non-Monotonicity of the Bargaining Set, the Kernel, And the Nucleolus of a Game[J]. SIAM Journal on Applied Mathematics, 1974, (2): 355-358.
