单根棉纤维与金属表面摩擦行为分析

2022-01-14闫哲朱存洲郭麟张有强

塔里木大学学报 2021年4期

闫哲，朱存洲，郭麟，张有强 ,2*

（1塔里木大学机械电气化工程学院，新疆阿拉尔 843300）（2新疆维吾尔自治区教育厅普通高等学校现代农业工程重点实验室，新疆阿拉尔 843300）

新疆棉花产量占全国总产量87.3%［1］，棉纤维束加工包括从田间收获到轧棉厂将纤维从种子上分离，最终将纤维转化为纱线或其他工程产品的单元操作。整个加工过程中，不同的机器部件将纤维拉、拽、抓住并彼此摩擦，直到他们排列成所需的形状或形式，由此引起棉纤维细丝之间、棉纤维束与加工设备部件表面不断摩擦，导致棉纤维束断裂、缠结和金属部件表面磨损。

为控制所需的棉产品质量，如良好的力学性能、尺寸精度和视觉外观等，对纤维材料摩擦性能的研究是非常有必要的。国内外学者对纤维材料种类、结构、材料表面状态及织造过程中张力、摩擦速率等其他因素的影响进行了大量研究［2-8］。肖振华等［9］在探究纤维摩擦性能时，提出纤维的压力与接触面积成指数关系的理论模型，通过对测试纤维在点接触与线接触两种接触方式下的摩擦性能的测试，得出纤维的横截面积及丝束方向、接触方式、外加载荷都会影响纤维的摩擦性能。MULVIHILL D M等［10］用自制的设备模拟碳纤维的摩擦行为，并建立了一种理想化接触模型，结果显示纤维束的排列方向及其表面上浆量都会改变纤维与金属表面接触时的实际面积，导致纤维的摩擦性能受到影响。CORNELISSEN B等［11］通过对碳纤维加工过程中碳纤维束的摩擦行为进行模拟，探究纤维束与金属表面的摩擦机理，并开发出一种基于宏观压力与宏观面积的比值等于实际法向力的数学关系的接触模型，较好地预测纤维与光滑表面的实际接触面积和摩擦因数。但对丝束与织物摩擦的比较是基于与表面接触的丝束材料数量大致相同的假设，存在一定的局限性。目前，大多数学者通过试验或建模的方法，得到纤维的摩擦性能与两者间的实际接触面积有关，但对两者间的摩擦现象的原理未作探究。

本研究在总结纤维材料与金属表面摩擦现象研究现状的基础上，对棉纤维束与金属表面的干摩擦行为提出合理的假设，考虑金属表面形貌对纤维摩擦性能的影响，通过建立接触力学模型的方法，揭示单根棉纤维的摩擦学行为，预测摩擦力的变化趋势，为纤维材料与金属表面的摩擦行为研究提供一定的理论基础。

1 模型建立

1.1 理论接触模型

纤维与金属表面的接触最普通的方式就是两个粗糙表面的接触，由于受表面粗糙度的影响，两个粗糙表面的真实接触主要发生在一些离散的微凸体上，两个表面开始进入接触时，最初接触只发生在几个微凸体上，接触表面承受法向载荷。随载荷的增加，更多的微凸体都逐渐进入相互接触的状态，同时也会使已发生的接触面积进一步增大，以承担更多的外加载荷，接触区发生的变形将产生抵抗外加载荷的应力，变形到一定程度时，应力与外加载荷保持平衡。

考虑到纤维束是由许多纤维细丝组合而成，其表面的不规则性至少比金属的低一个数量级左右，所以假定纤维细丝是一个个光滑的圆柱体，接触通常发生在柱体表面。对于粗糙表面与光滑表面之间的弹性和弹塑性混合接触的问题，GREENWOOD J A和WILLIAMSON J［12］提出的一个经典的统计接触模型（GW模型）：假设表面上分布很多微凸体，且微凸体顶端为球体；表面的微凸体顶端半径相同；微凸体的高度是随机变化；表面上的微凸体峰高服从高斯分布，如图1所示。实际上许多表面服从高斯分布，但关于微凸体的半径为常数的假设是不成立。

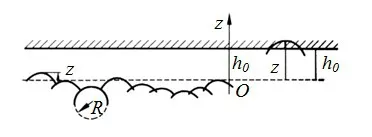
图1 GW随机表面模型

GREENWOOD J A 和 TRIPP J H［13］对粗糙表面的接触问题分析发现，对于微凸体形状及分布不规则的两个粗糙表面，接触大多发生在微凸体侧面，如果表面峰高服从于高斯分布，那么微凸体形状及其在单个或者两个表面的位置对接触的影响不太重要，故微凸体顶端被假定为球形以便于数值计算。因此，基于GW模型对粗糙表面接触模型的考虑，需要对金属表面的粗糙峰尺寸形状和高度分布等进行一定的假设：粗糙表面各向同性；粗糙峰峰顶近似球体，峰顶曲率半径相同，且高度服从高斯分布；粗糙峰之间不会互相影响；接触过程中不发生变形。

通过上述假设，单根棉纤维与金属表面的接触类似于圆柱体纤维细丝与多个粗糙峰接触。对于单个接触点，单个小粗糙峰与纤维细丝之间的接触类似于一个弹性光滑表面与一个球体单峰相接触。考虑到金属硬度远大于纤维材料，所以假设两者之间的接触始终为弹性。接触模型如图2所示，其中F为法向力，d为法向变形总量，R为粗糙峰当量曲率半径，a为接触面积半径。根据赫兹接触理论，接触区面积类似一个圆，且随着法向载荷的增加，变形量增大，实际接触面积也会增大。

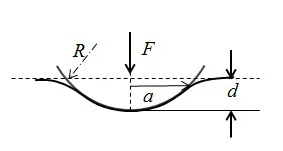
图2 弹性光滑表面与球体单峰的接触

1.2 理论摩擦力模型

接触面积与摩擦力（Ff）的关系是摩擦学研究中最重要、最具挑战性的问题之一。经典阿蒙顿定律指出，摩擦因数与表观接触面积无关。后来研究人员逐渐认识到，由于表面粗糙度的影响，实际接触面积只占整个表观接触面积的小部分，显然摩擦只发生在这些小区域。常用经典库伦摩擦定律表示两种材料之间的滑动摩擦。

式（1）中：μ为库伦摩擦系数，N为法向力。库伦摩擦定律提出摩擦系数与材料性质有关，且为固定值，即摩擦力与法向力成正比。但对于纤维和其他复合材料来说，Ff与N不存在线性关系，对此HOWELL H G等［14］提出了修正公式。

式（2）中：N为法向力；t、n为实验拟合参数，t与纤维材料性质有关；n由接触点变形机制决定，n取值范围为2/3～1，当材料发生完全弹性变形时n为2/3，当材料发生完全纯塑性变形时n为1。

ROSELMAN I C等［15-16］通过对单根纤维的摩擦行为观测后提出，Ff由接触材料的界面剪切强度（τ）与两者的实际接触面积（Ar）的乘积和犁沟力（P）共同决定。

P对纤维束Ff的影响比较小，因此在当前模型中被忽略。研究表明使用纤维束进行100多次测量后，金属滚筒表面未受影响，且未观察到材料转移到金属滚筒，同时纤维束中纤维细丝也无任何损伤［17］。此外纤维细丝的细度导致相对较低的弯曲刚度，使纤维与金属表面粗糙峰之间形成良好的接触，进一步减小犁沟力的影响。

2 材料与方法

2.1 棉纤维束材料

纤维细丝所受负载与纤维束在金属表面的实际接触根数相关，考虑到单根纤维细丝所受负载较小。为方便计算与分析，假定纤维细丝所承受的法向载荷Nfil变化范围为0.1～1.0 N/m之间。棉纤维束选取新疆长绒棉，其棉纤维细丝的基本参数如表1所示。

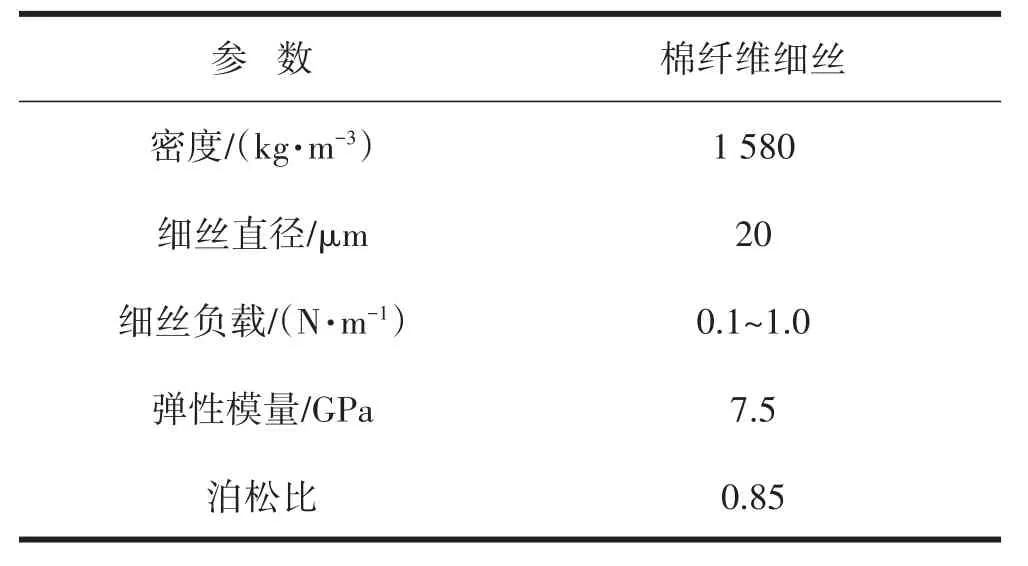
表1 棉纤维细丝的基本参数及对应值

2.2 金属表面形貌

大量的绞盘实验［17］摩擦结果表明牵引端力随金属材料的粗糙度特征而变化，金属表面的微观几何特性强烈影响表观摩擦系数［16］。故本研究选取粗糙度为（0.020±0.003）μm的光滑金属样品和粗糙度为（1.100±0.400）μm的粗糙金属样品，对两种样品分别进行三维形貌扫描，粗糙金属表面叠加（0.016±0.003）μm的小粗糙度，得到金属表面形貌如图3、图4，具体参数见表2。

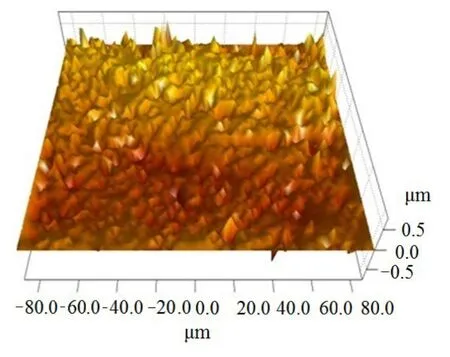
图3 光滑金属表面形貌

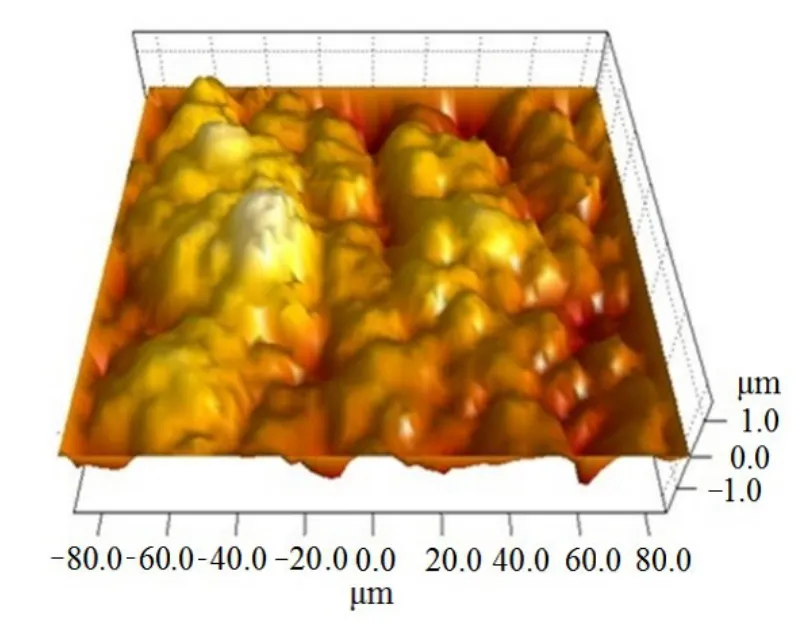
图4 粗糙金属表面形貌

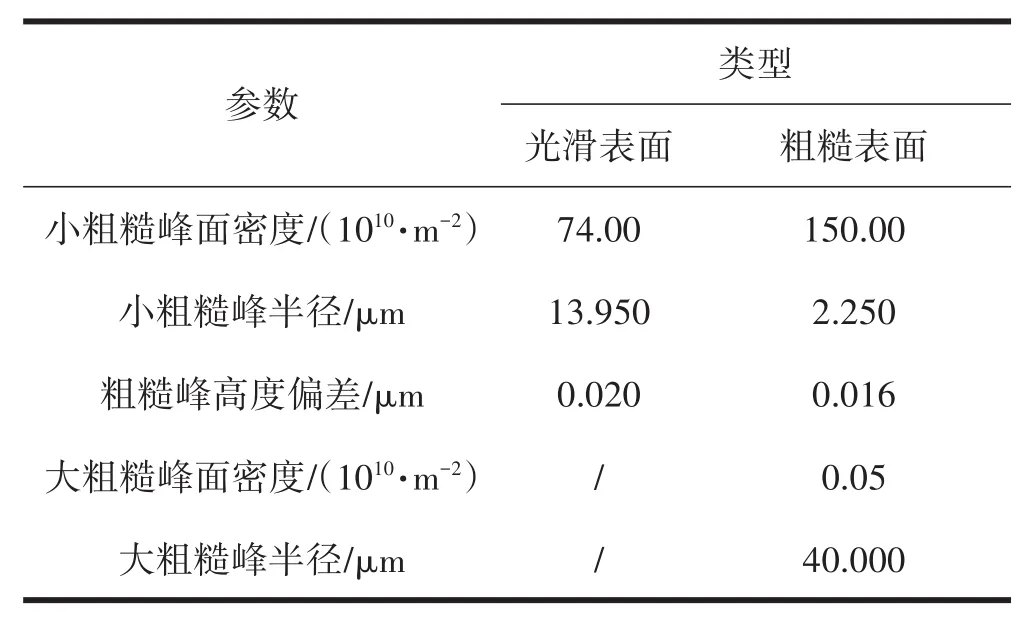
表2 两种不同粗糙度的金属样品形貌参数及对应值

2.3 计算方法

本研究提出一种分析接触力学模型的方法来描述单根棉纤维与金属表面接触时的摩擦行为。在确定系统中相关的接触载荷后，所提出的模型分析方法由确定纤维细丝与金属表面之间接触面积的两步过程组成。首先，用赫兹接触理论，计算纤维丝与金属表面之间的名义接触面积。其次，考虑金属表面真实的微几何形貌，计算两者的实际接触面积［18］。

3 结果与分析

3.1 名义接触面积

名义接触面积是指在这一步的计算中假定完全理想的金属表面微观几何的接触，采用赫兹接触理论分别对两种不同金属表面形貌下的接触面积进行计算。

3.1.1 光滑金属表面名义接触面积

在纤维细丝的半径范围内，光滑金属表面的粗糙峰尺寸较小，纤维细丝与光滑金属表面接触类似于圆柱与光滑表面之间的接触，如图5所示。

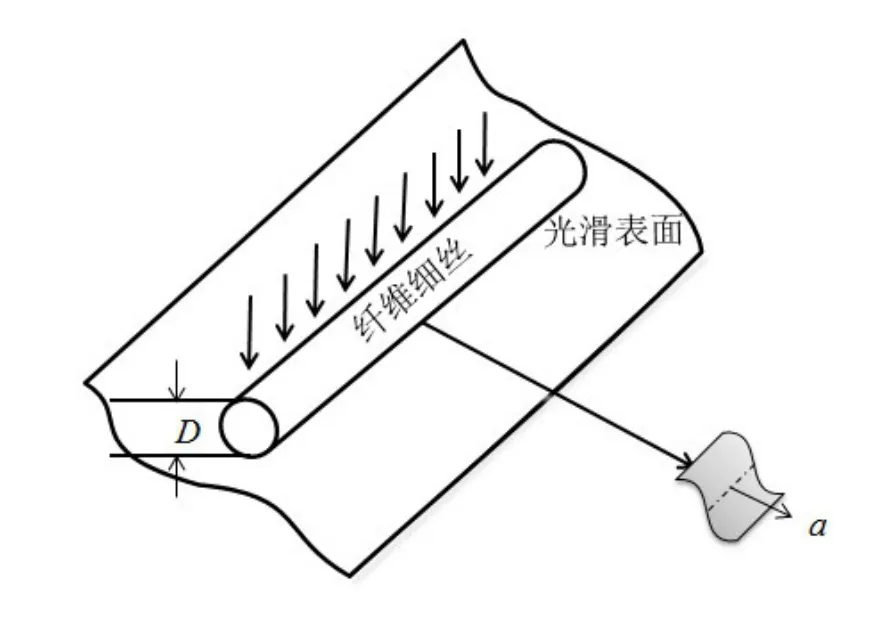
图5 纤维细丝与光滑表面接触

对于光滑金属表面形貌两者之间接触为线接触，接触区面积为：

式（4）中：a为接触区半宽，mm；Nfil为作用在纤维细丝上的法向负载，N；Rm为接触体的平均曲率半径，mm；E*为材料的等效弹性模量，GPa。

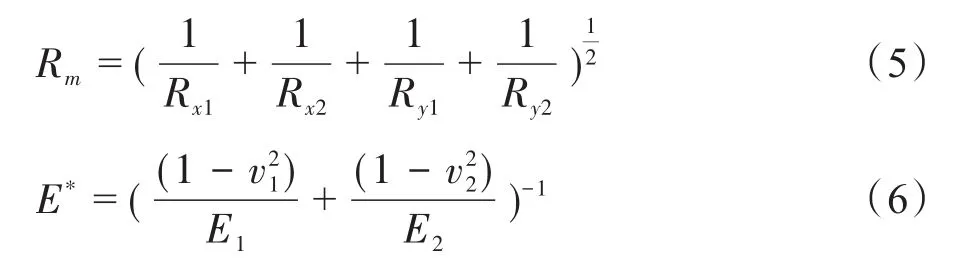
式（5）、式（6）中：Rx1、Ry1分别为纤维细丝横向与轴向曲率半径，mm；Rx2、Ry2分别为光滑金属表面粗糙峰横向与轴向平均曲率半径，mm；E1为纤维细丝的弹性模量，GPa；E2为金属的弹性模量，GPa；v1为纤维细丝的泊松比，v2为金属的泊松比。其中Rx1=Rfil；Rx2=∞；Ry1=Ry2=∞。

纤维细丝在光滑金属表面的名义接触面积An1=2a，且光滑接触的名义接触面积与分布正态载荷的平方根成正比。

3.1.2 粗糙金属表面名义接触面积

在纤维丝半径范围内，粗糙金属表面存在尺寸较大的非球面，纤维细丝与粗糙金属表面接触可类比于圆柱与球体［19］之间的接触，接触面积近似椭圆形接触区，如图6所示。

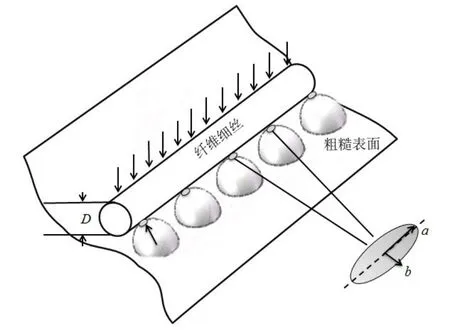
图6 单根纤维与粗糙表面接触

对于粗糙金属表面形貌，两者之间的接触为点接触，名义接触面积由几个较大的椭圆接触区组成。接触区面积为：

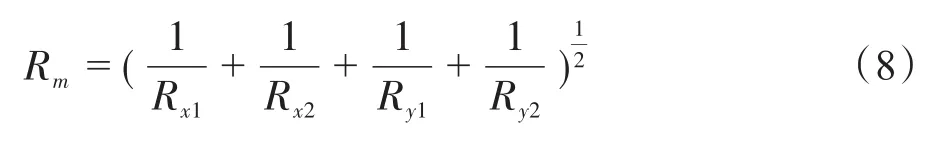
式（8）中：Rm为平均有效曲率半径，mm；纤维细丝横向与轴向平均曲率半径满足：Rx1=Rfil，Ry1=∞；金属表面粗糙峰横向与轴向平均曲率半径满足：Rx2=Ry2=βsmall；椭圆接触面积的长半径和短半径分别为a和b。

式（9）、式（10）中：E*为杨氏弹性模量，GPa；Nasp为单个粗糙峰上的负载，N/m；α、β是引入的无量纲参数。

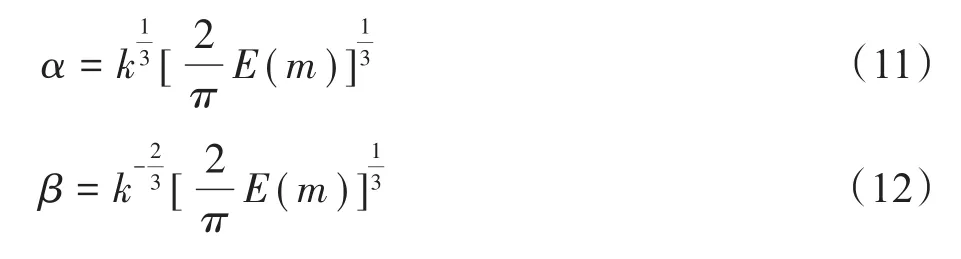
其中椭圆率k=a/b时，k有以下关系：

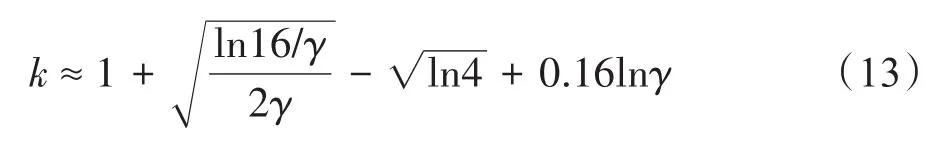
满足γ=Rx/Ry，0＜γ≤1，曲率半径Rx、Ry为：

其中第二类完全椭圆积分E(m)近似为［19］：

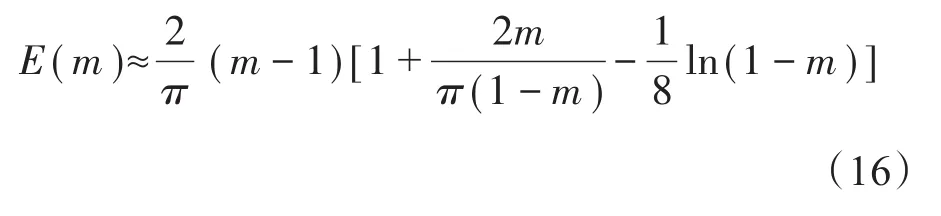
式（16）中m=1-k2，可利用Matlab对E(m)的数值进行计算验证。最终圆柱形细丝与粗糙金属表面单个粗糙峰的名义接触面积（Aasp）表达式为：

基于三维共焦显微镜表征的粗糙金属表面形貌，单根纤维细丝与金属的接触大约有2.36×104个点，由于在给定的法向载荷Nfil下，每个粗糙峰的接触面积是均匀的，得到纤维细丝与金属间的名义接触面积（An2）表达式为：

粗糙接触的名义接触面积与分布正态载荷的满足：

3.2 实际接触面积

在名义接触面积内的实际接触面积是由粗糙峰高度（Z）分布决定的，受粗糙峰高度偏差（σsmall），小粗糙峰面密度（ηsmall）和小粗糙峰半径（βsmall）共同影响，随着载荷的增加，纤维细丝与金属表面的分离距离（d）逐渐减小，实际接触面积随之增加，如图7所示。

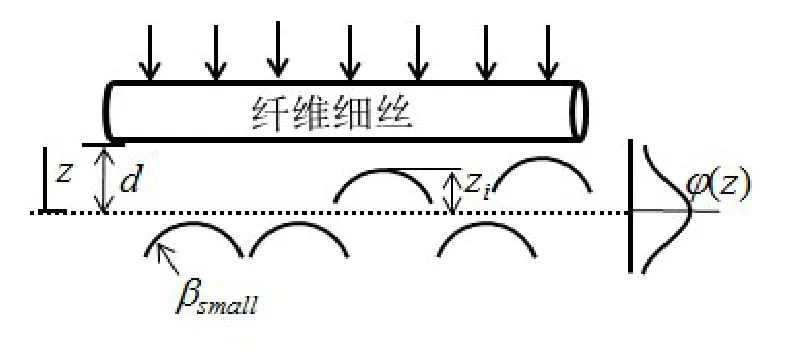
图7 粗造表面统计形貌

根据前文提出的理论接触模型，与单个粗糙峰的接触面积尺寸相比，纤维细丝的曲率半径非常大，细丝表面可近似为一个平面，两者之间的接触为粗糙峰与弹性平面之间的接触，实际接触面积（Ar）为名义接触面积（An）的概率密度函数［12］。

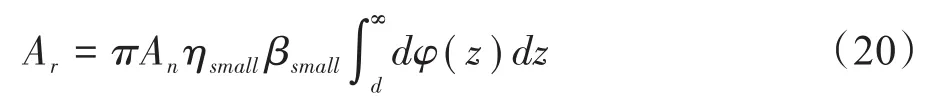
式（20）中φ(z)是粗糙峰的峰高的正态分布概率密度函数，当粗糙峰高度偏差满足σ=σsmall时［19-20］：

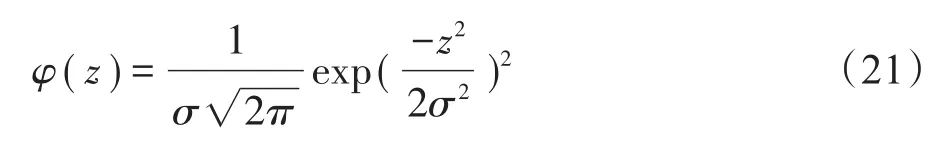
加载后，金属表面的粗糙峰以Zi-d的距离压入纤维细丝表面，造成微接触，单个微接触的总和构成纤维细丝与金属表面之间的实际接触面积。

3.3 模型计算

将棉纤维细丝参数与两种金属表面形貌参数代入上文推导的公式，基于数值计算得到两者的真实接触面积。

从图8可知，随着法向负载的增加，棉纤维细丝与金属表面之间实际接触面积也在增加；棉纤维细丝在光滑表面上的实际接触面积始终大于粗糙表面上的实际接触面积，且两者的比值约为30%～35%（该比例仅适用于纤维细丝法向负载Nfil=0.1～1.0 N/m的条件下）。

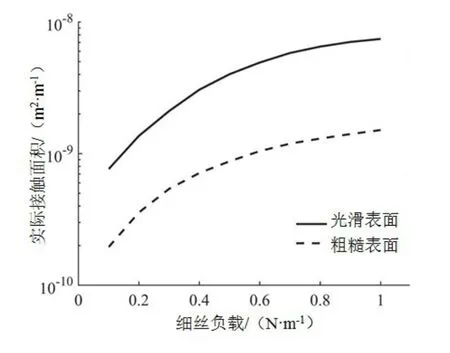
图8 棉纤维束与金属表面的真实接触面积

3.4 模型预测

τ是预测Ff的重要参数，但τ值的测定方法较为复杂，且目前为止对本研究所讨论体系的界面抗剪切强度的精确测量还没有发表，在该模型中，对τ进行有根据的假设。有研究发现碳纤维类材料在不同金属表面上滑动时τ值从20～100 MPa不等，石墨纤维最高理论上限为600 MPa［21］。预计柔软的棉纤维束的τ值比碳纤维的小，故本研究选τ为10 MPa、100 MPa两种界面剪切强度作为参考值。根据式（2）和式（3），对纤维细丝的Ff与所受载荷进行最小二乘法拟合可得拟合参数如表3。

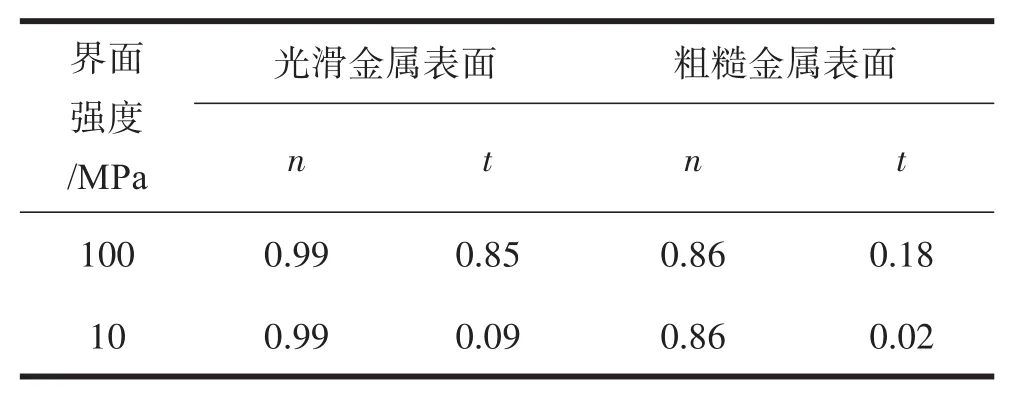
表3 拟合参数

根据棉纤维细丝的摩擦特性可预测棉纤维束的Ff变化，随着法向力的增加，纤维细丝与金属表面的实际接触根数也随之增加。对棉纤维束在不同法向载荷下的接触横截面面积进行观测，发现其受负载影响较小，可假设实际接触的棉纤维细丝根数不变。根据上文假定的载荷范围，可设定棉纤维束所受法向负载为0.1～1.0 N/m，根据式（2）对棉纤维束与金属表面Ff进行预测，结果如图9、图10所示。

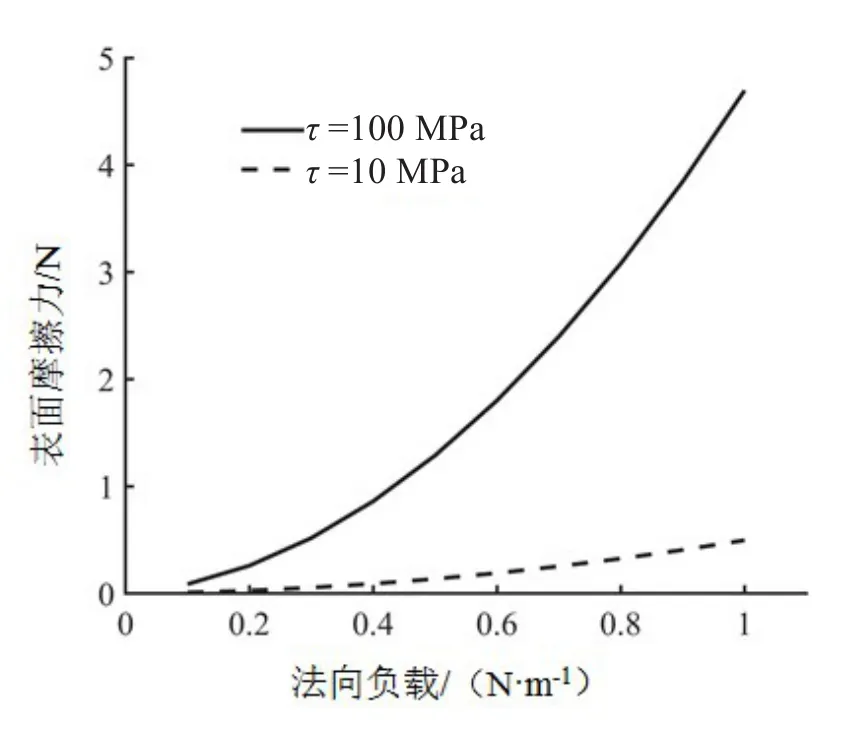
图9 光滑表面预测摩擦力

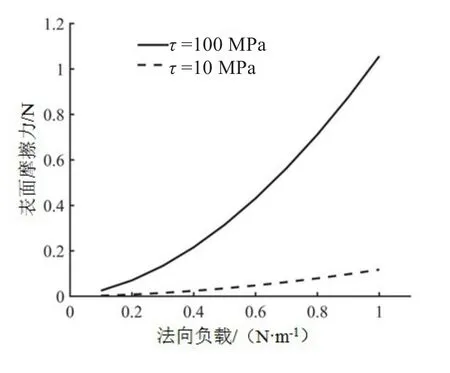
图10 粗糙表面预测摩擦力

本研究假设τ参数是特定于界面但独立于表面形貌，故对于光滑和粗糙两种金属表面形貌采用相同的τ值。结果表明棉纤维束在光滑金属表面上的预测摩擦力大于在粗糙金属表面上的预测摩擦力。

预测值显示Ff随金属表面粗糙度的增大而减小，与基础的摩擦学规律不一致，这一现象可从本研究的接触力学模型进行解释。由式（3）可知，在τ一致的情况下，Ff取决于实际接触面积。由图7可知粗糙峰高度Z是影响纤维细丝与金属表面实际接触面积的重要因素，前文1.1提到粗糙峰高度服从高斯分布，接触发生在粗糙峰球形顶端。对于两者的接触，实际接触区只占名义接触区域的很小部分，随金属表面粗糙度的增大，粗糙峰高度随之增大，与棉纤维束的实际接触区面积逐渐减小，最终导致Ff的减小。