BiPLS结合SPA对苹果可溶性固形物含量的近红外检测方法

张立欣，杨翠芳，陈杰，王亚明 ，张晓*

（1塔里木大学信息工程学院，新疆 阿拉尔 843300）（2南京理工大学理学院，江苏 南京 210094）

中医认为苹果具有生津止渴、润肺除烦、健脾益胃、养心益气等功效，并且味道酸甜适口，营养丰富，因此，深受人们的喜爱。但是由于环境因素、土壤特征等条件的不同，导致各地苹果的品质存在差异。消费者在购买水果时，除了注重颜色、大小、形状等外部品质外，对内部品质口感也是极为看重，其中可溶性固形物含量直接影响其口感［1］。传统可溶性固形物含量的检测方法是破坏性或侵入性测量，不仅费时、费力，而且破坏了水果的完整性。近些年，NIR分析技术因具有快速、便捷、无损的优点逐渐被用于农产品的检测中，如水蜜桃［2］、红提［3］、滑皮金桔［4］、灵武长枣［5］等。魏康丽等［6］采用单积分球技术定量分析苹果低温贮存（0℃，150 d）期间可溶性固形物、总可溶性糖、果糖、葡萄糖及蔗糖与吸收和散射性质的关系，该研究为光学技术检测果实品质提供了理论参考。王浩云等［7］提出了一种基于高光谱图像与三维卷积神经网络（3D-CNN）的苹果高光谱多品质参数同时检测方法，建立的糖度模型相关系数高达0.827。刘燕德等［8］为了实现不同产地苹果糖度的快速在线无损检测，减少产地差异对近红外光谱检测模型的影响，建立了苹果糖度的UVEPLS通用模型，提高其他产地样本糖度的预测稳健性。徐永浩等［9］验证了微型近红外光谱仪(NIRscan)用于苹果糖度的现场快速和高精度无损检测具有可行性。谭保华等［10］设计了水果含糖量的近红外检测实验系统。乔鑫等［11］设计了手机联用的苹果糖度便携式检测装置，通过优选特征波段确定适合苹果糖度检测的波段范围及光学传感器，完成苹果糖度的高效、便携及低成本的无损检测。在这些光谱分析中，全谱中不可避免地含有大量噪声、无信息甚至是干扰的变量，这些变量的存在不仅增加了多元校正模型的复杂程度，还有可能影响模型的预测性能，因此在建立模型前，需要提取特征变量，变量选择已成为近红外光谱分析中的一个重要步骤。特征波段的提取主要有SPA［12-13］，竞争性自适应重加权算法（CARS）［14］、主成分分析（PCA）［15］等，或者几种方法同时使用［16］，选择的对象一般是单一光谱变量，选择光谱区间对苹果可溶性固形物含量的检测鲜有报道。

朱绍农等［17］采用偏最小二乘法结合区间以及后向区间法对全谱进行变量筛选，构建形成iPLS和Bi-PLS定量分析土壤样品中铜、镍元素含量的模型。张丙芳等［18］结合近红外光谱分析技术，利用间隔偏最小二乘-连续投影算法进行特征波段选择，建立一个适于检测油脂中酸值和羰基价变化，且精确度较高的模型。饶利波等［19］用后向区间法选出177个特征波长，结合竞争性自适应重加权算法再进一步筛选，提取出7个特征波长，利用偏最小er乘法建立基于特征波长的可溶性固形物含量检测模型，证明了后区间法结合竞争性自适应重加权算法在提高苹果可溶性固体物含量检测精度方面的有效性。

由于不同样品内部结构不同，特征光谱区间也不同。本试验以阿克苏‘红富士’苹果为研究对象，基于近红外光谱技术对苹果中的可溶性固形物含量进行分析，建立PLS模型，研究区间变量选择方法和单一变量选择方法相结合，对定量分析性能提升的影响。

1 材料与方法

1.1 供试材料

以阿克苏的‘红富士’苹果为实验对象，在实验中所使用的苹果均产自红旗坡农场，挑选的苹果表面没有缺陷、直径范围为65～85 mm、大小均匀，去除表面的污垢，放置在冰箱内保存，温度控制在4℃，实验前分批拿出，待其恢复到室温(20～25℃)环境后开始实验。

实验中所用的高光谱系统为北京卓立汉光公司的Hyperspectral Sorting System推扫式高光谱分选系统，光谱测定的范围为900～1700 nm(实际可测量到1750 nm)，采用卤钨灯为光源，光谱分辨率5 nm，光谱采样点4 nm，对样品进行扫描，获取影像和光谱信息，通过自带的ENVI 4.7软件获取每个样品的光谱值，导出为Excel文件。

1.2 实验方法

1.2.1 可溶性固形物含量的检测

选用糖度盐度两用仪(MASTER-BX/S28M)，对采集过高光谱图像的苹果部位挖取适量果肉，深度为皮下0.5 cm左右，压榨出汁水，对可溶性固形物含量进行测量，测量3次取平均值，以此来作为苹果可溶性固形物含量的标准值。

1.2.2 建模方法

PLS算法的建模思想主要是从自变量和因变量矩阵中提取第一主成分，并求得协方差，再提取第二主成分，求得协方差，依次类推，最后根据交叉验证的结果，建立最终的偏最小二乘定量回归预测分析模型。它集多元线性回归分析、典型相关分析和主成分分析的基本功能为一体，特别适合变量之间有多重共线性的场合［19］。

1.2.3 特征变量选择方法

iPLS是将数据集均分成同等宽度的小区间，建立每个子区间的PLS模型，再根据各个模型的交叉验证结果优选出最佳的光谱波段［19］。与全光谱变量建模相比，可以减少建模所用变量，但是由于只选一个区间建模，有可能会丢掉其他区间的有效信息。

BiPLS是在iPLS的基础上进行多次计算，并依次减少交叉验证表现最差的区间，直到剩下一个数据区间，进而得出交叉验证结果最小，即预测效果最好的波段集合［20］。可以克服单一区间建模的缺点，选取更多区间的有效信息。

SPA通过计算光谱矩阵中某一波长对其他波长的投影，在该波长序列中选取投影量最大的波长作为下一个波长，序列中的每个波长都与前一个波长相关性最小，能最大程度消除共线性对模型的干扰，降低建模过程的复杂度［20］。该算法简要步骤如下：

记初始迭代向量为xk(0)，需要提取的变量个数为N，光谱矩阵为J列。

1）任选光谱矩阵的1列（第j列），把建模集的第j列赋值给xj，记为xk(0)。

2）将未选入的列向量位置的集记为s，即：

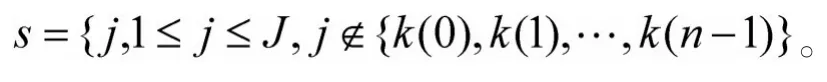
3）分别计算xj对剩余列向量的投影：

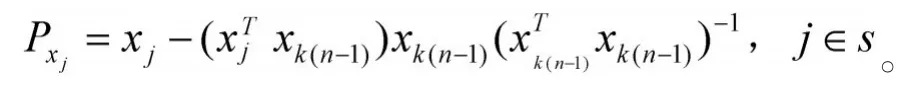
4）提取最大投影向量的光谱波长：

6）n=n+1，若n＜N，则按步骤1）～6）循环计算。

1.2.4 模型验证

将数据分为训练集和测试集，依靠训练集建立模型，测试集将通过已经建立好的模型进行验证，以测试集的均方根误差、相关系数作为标准来评判模型的优劣，均方根误差越小，相关系数越大，模型的预测效果越好。其计算公式为：

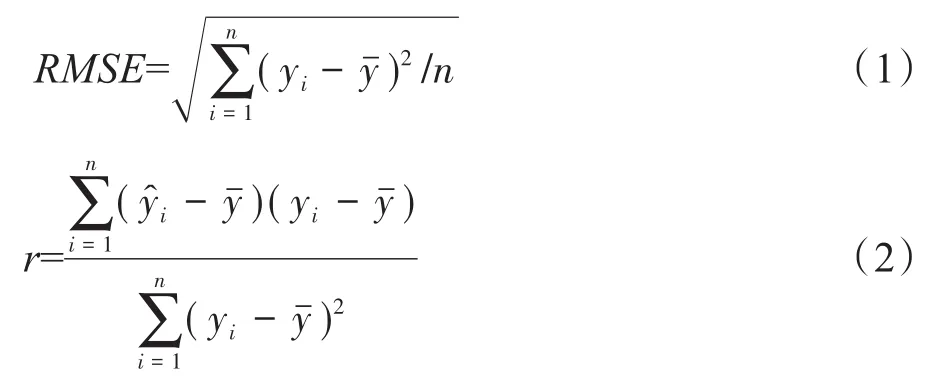
式（1）、式（2）中，RMSE：均方根误差；r：相关系数；n：样本个数；yi：第i个样本的观测值第i个样本的预测值（i=1,2,3,…，n）；yˉ：观测值的平均值。

2 结果与分析

采集的‘红富士’苹果高光谱数据中，剔除异常值后，共得到160个样本，其原始光谱曲线如图1所示。近红外光主要是对含氢基团X—H（X为C、N、O）振动的倍频和合频吸收，其中包含了大多数类型有机化合物的组成和分子结构的信息。选用连续改变频率的近红外光照射某样品时，由于试样对不同频率近红外光的选择性吸收，通过试样后的近红外光线在某些波长范围内会变弱，透射出来的红外光线就携带有机物组分和结构的信息。由图1分析可知，950 nm波段附近处有一个明显的峰，这是O—H基团的3倍频吸收带，1060 nm波段处的峰是N—H基团的3倍频带，1180 nm处的波谷位于C—H的3倍频带，1440 nm处的波谷是H2O的2倍频吸收带等，这些化学键又是组成水分、可溶性糖等物质的基础形式，如果样品的组成相同，则其光谱也相同，反之亦然。因此，近红外光谱分析法是一种间接的分析技术，如果建立了光谱与可溶性固形物含量的对应关系，那么只要测得样品的光谱，就能很快预测其可溶性固形物含量。

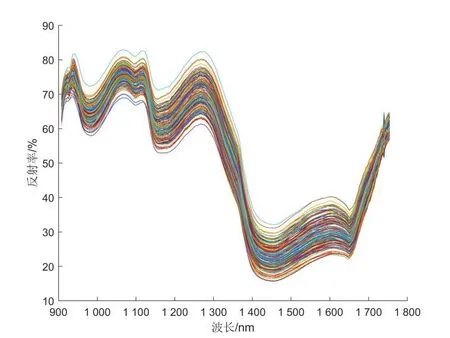
图1 原始光谱图

从图1可以看出，光谱曲线比较分散，采用多元散射校正(multivariate scatter correction，MSC)对光谱数据进行预处理，预处理之后的光谱曲线如图2所示，分析可知，预处理之后，光谱的重合度变高，减弱了散射对原始光谱的影响。

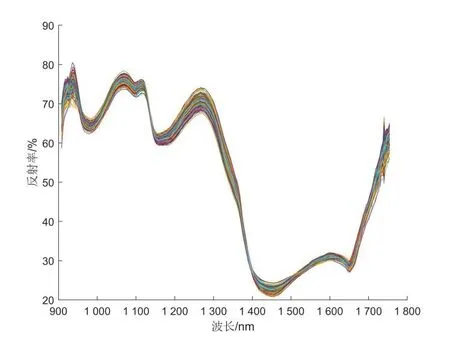
图2 预处理之后的光谱图

采用Kennard-Stone算法将数据集以3∶1的比例划分为训练集和测试集，训练集和测试集的划分结果如表1所示。测试集的数据都落在训练集数据范围之内，说明数据的划分是合理的。

表1 训练集和测试集中的可溶性固形物含量

2.1 PLS模型

在PLS建模过程中，潜变量数目（LV）的选择尤其重要，若LV过小，会导致光谱中较多信息的丢失，造成欠拟合；若LV过大，造成过拟合，影响模型的泛化能力。本研究以交叉验证的均方根误差最小来确定模型的最佳潜变量个数。采用全光谱波段建模，交叉验证的均方根误差和潜变量的关系如图3所示，分析可知，交叉验证均方根误差(RMSECV)的值随着LV的增加而减小，当LV增加到4时，RMSECV值基本趋于平缓，以后再增加LV值，RMSECV并无明显增加的趋势，为避免出现过拟合，因此LV可以取4。选择潜变量个数为4，建立苹果中可溶性固形物含量的全光谱PLS模型。训练集和测试集的建模结果如图4所示，训练集的r=0.8304，RMSE=1.1177，测试集的r=0.7694，RMSE=1.3483。

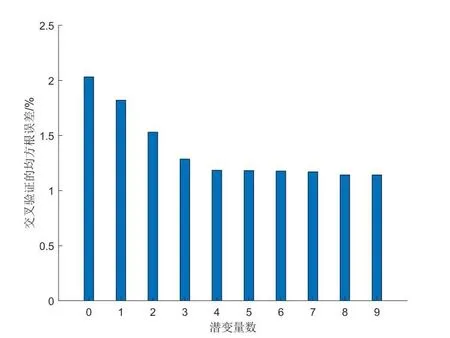
图3 不同潜变量数对应的交叉验证均方根误差

图4 PLS模型的预测结果

2.2 iPLS模型

由于光谱能够体现物质所含成分及含量，但同时包含大量的冗余信息，因此，需要提取特征波长。利用iPLS方法，将全光谱波段依次按10～25个区间进行等分(若不能等分，则最多相差一个波段)，并在每一个区间建立PLS回归模型。将每次等分获得的最小RMSECV作为衡量标准，来确定建模的光谱子区间。结果如表2所示，在区间划分过程中，当划分为20个小区间时，对应的第2个子区间的RMSECV最小，故选择第2个子区间的光谱波段作为iPLS模型的输入自变量。

表2 不同区间个数的iPLS模型的RMSECV

建立可溶性固形物含量的iPLS模型，模型的预测结果如图5所示，训练集的预测结果r=0.8478，RMSE=1.0640，测试集的预测结果r=0.8189，RMSE=1.5053。

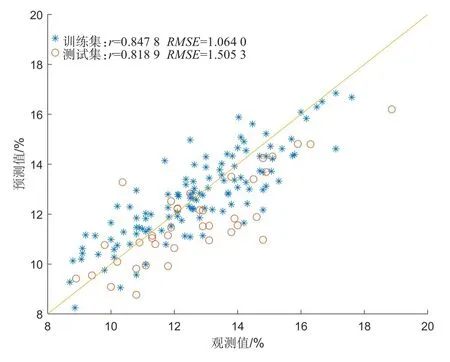
图5 iPLS模型的预测结果

2.3 BiPLS模型

虽然iPLS模型对数据进行了筛选，但是由于只取了一个子区间，忽略了多区间建模效果更优的可能性，所以可能会丢掉一些其他区间的有效信息，因此，采用BiPLS模型选取子区间的组合来建模。

由于在采用BiPLS模型选取子区间时，间隔大小能够影响波长范围的选取，间隔过小，会使得到的结果太过复杂，间隔过大，会丧失一部分有用信息。由于从理论上无法确定最佳的间隔数，所以尝试采用10～25个间隔数，将全光谱分成等宽度的子区间(若不能等分，则最多相差一个光谱波段)，并挑选出RMSECV值最小的子区间组合作为建模的光谱区间，表3为不同间隔数的BiPLS模型选取的结果。由表3分析可知，以均方根误差最小为标准，当划分为14个小区间，并选取其中的3个小子区间组合时，所建模型的RMSECV值最小。这3个子区间分别为第9、11、12子区间，选取在这3个子区间上的54个波长变量建模。

表3 不同间隔数下BiPLS模型的RMSECV

BiPLS训练集和测试集的预测结果如下图6所示，训练集的预测结果r=0.9167，RMSE=0.8015，测试集的预测结果r=0.8978，RMSE=1.0119。相比较于PLS和iPLS模型，BiPLS模型的预测性能明显提升。

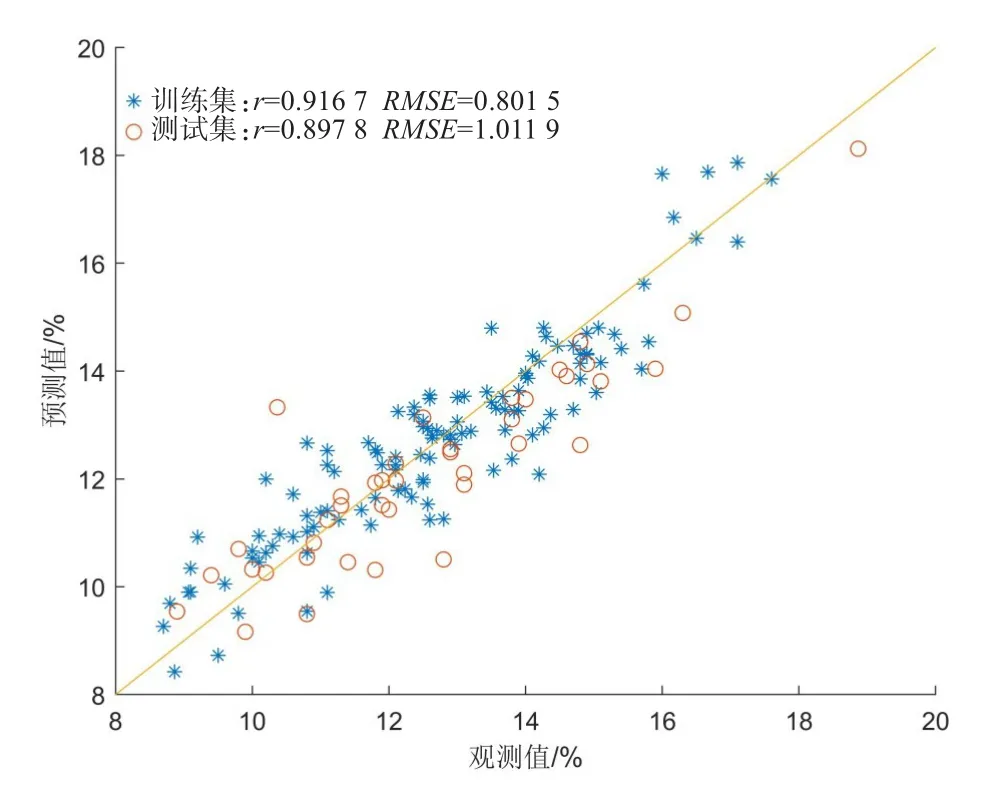
图6 BiPLS模型的预测结果

2.4 SPA-PLS模型

若对全光谱波段直接采用SPA算法提取特征波长变量，以均方根误差最小来确定最终选取的变量，指定波长变量数为2～20。选取过程如图7所示，分析可知，随着所选变量个数的增加，均方根误差呈现先减少后增加的趋势，当所选变量个数为8时，均方根误差最小为1.0648。因此，最终选取8个波段变量，波长分别为917.29 nm、939.16 nm、961.12 nm、1110.91 nm、1334.81 nm、1697.27 nm、1732.84 nm、1743.55 nm，即为图8中小方框所对应的横坐标。

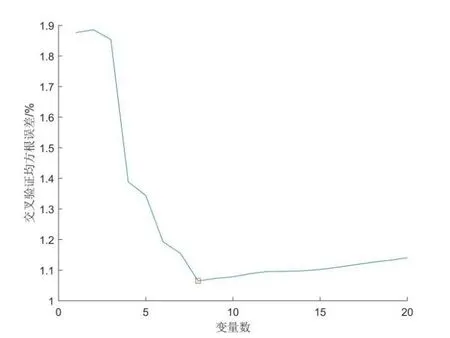
图7 SPA选取变量

图8 SPA选取的变量

以此8个波长变量作为输入自变量，建立PLS模型，训练集和预测集的预测效果如图9所示，训练集的预测结果显示r=0.7556，RMSE=1.3141，测试集的预测结果显示r=0.6753，RMSE=1.5490。

图9 SPA-PLS模型的预测结果

2.5 SPA-iPLS模型

iPLS模型将全光谱区间划分为20个小区间，对应的第2个子区间建模输入自变量，但是没有考虑输入变量之间的共线性。对第2个小子区间采用SPA算法提取特征波长变量，以均方根误差最小来确定最终选取的变量。最终选取3个波段变量，波长分别为951.7 nm、964.27 nm、976.86 nm，以此3个波长变量作为输入自变量，建立PLS模型，训练集和预测集的预测效果如图10所示，训练集的预测结果显示r=0.7561，RMSE=2.4159，测试集的预测结果显示r=0.7248，RMSE=1.8354。

2.6 SPA-BiPLS模型

BiPLS模型选取子区间的组合作为建模输入自变量，但是没有考虑输入变量之间的共线性。为提高模型的稳健性，避免共线性的影响，对BiPLS选出的变量采用SPA算法提取特征变量，指定波长变量数为2～10，采用均方根误差最小来确定最终变量个数，变量选取过程和结果如图11所示,分析可知，刚开始，随着所选变量个数的增加，均方根误差呈现递减的趋势，当选取变量个数为6时，均方根误差为0.4652，之后随着所选变量个数的增加，均方根误差并无明显减少的趋势，因此，选取6个波长变量参与建模，对应的波长分别为：1381.97 nm、1402.29 nm、1522.14 nm、1556.80 nm、1584.66 nm、1626.66 nm。以这6个波长变量为输入自变量来建立模型，训练集和测试集的预测结果如图12所示，训练集的预测结果显示r=0.8919，RMSE=0.9073，测试集的预测结果显示r=0.8981，RMSE=0.9371。与BiPLS模型相比，参与建模的变量个数从54个减少到6个，提高了运行效率。

图12 SPA-BiPLS模型的预测结果

所建立的6种模型的总结果如表4所示。

表4 模型对比

由表4可知，分别采用整个的波长区间、一个子区间、组合的子区间所建立的PLS、iPLS、BiPLS模型，选取的变量个数在13～254之间，预测效果最好的是BiPLS模型。分别对这3种区间采用SPA算法选取特征变量，所选取的变量个数在3～8之间，建模变量个数的减少有益于提高运行效率，但是所建立的SPA-PLS、SPA-iPLS模型预测精度降低了，仅有SPABiPLS模型预测精度稍有提高。

3 讨论与结论

全光谱波段建立PLS模型，254个变量参与建模，由于掺杂了过多的干扰信息，导致模型的泛化能力较差。iPLS模型中，当区间划分为20个小区间，以第2个子区间的波长变量参与建模时，虽然训练集表现优于PLS，但是测试集的RMSE却变大了，这是由于iPLS模型剔除了部分有用信息，造成模型的欠拟合。BiPLS模型在iPLS的基础上选取了更多的子区间来建模，训练集和测试集的预测效果优于PLS和iPLS模型。对全光谱波段，采用SPA算法，去除了共线性的影响，但是有效变量之间的距离不一定最大，因此，筛选出的变量子集中可能包含一些无用信息，甚至是干扰信息，降低模型的泛化能力。由于iPLS模型剔除了部分有用信息，故SPA-iPLS模型欠拟合。在BiPLS模型所选组合的光谱子区间的基础上，采用SPA算法，选取6个特征波段变量，建立SPA-BiPLS模型，去除了共线性的影响，提高了运行效率。

采用GUO Z M等［13］的CARS方法提取12个特征变量建模，训练集的预测结果显示r=0.9332，RMSE=0.7210，测试集的预测结果显示r=0.8932，RMSE=1.0158。采用WU Y等［14］的PCA方法提取5个主成分建立模型，训练集的预测结果显示r=0.4371，RMSE=2.5560，测试集的预测结果显示r=0.2166，RMSE=2.3483。采 用 ZHANG D Y 等［15］的 CARS-SPA方法提取7个特征变量建模，训练集的预测结果显示r=0.8957，RMSE=0.7954，测试集的预测结果显示r=0.8608，RMSE=1.2404。采用饶利波等［19］的CARS-BiPLS方法提取13个特征变量建模，训练集的预测结果显示r=0.9360，RMSE=0.4985，测试集的预测结果显示r=0.8750，RMSE=1.0511。效果均不及SPA-BiPLS模型的，这是因为PCA方法只是对自变量做了重新组合，并没有考虑因变量的影响，因此，建模的精度最低。CARS、CARS-BiPLS方法无法克服变量之间共线性的影响，这都将会影响模型的泛化能力。CARS-SPA虽然去除了共线性的影响，但也剔除了部分有用信息，导致欠拟合。

总之，采用BiPLS算法选出组合的光谱子区间，保留了更多的光谱信息，在此基础上与SPA相结合，一定程度上实现了算法之间的优势互补，提高模型的预测效果。