等离子体中在极板上运动的介质颗粒的带电量测量

郭志强，孙文涛，蔡雅文，张宁，张顺欣，贺亚峰

(河北大学 物理科学与技术学院，河北 保定 071002)

尘埃等离子体物理是近20年来发展起来的一个新的研究方向.尘埃等离子体是由电子、离子、中性原子以及大量带电的固态弥散微粒子组成的系统[1-3]，在宇宙天体空间中到处都充斥着尘埃等离子体,近年来关于等离子体的研究同样处于快速发展阶段[4-6].到目前为止，各领域的学者在尘埃等离子体系统中观察到了许多新的物理现象，如尘埃颗粒的充电过程[7]、实验室等离子体中尘埃颗粒的产生[8]、单个尘埃颗粒在等离子体鞘层中的受力及其运动情况[9]、尘埃等离子体中的非线性结构[10]、凝聚结晶[11]以及尘埃晶格在磁场作用下的旋转[12]、等离子体中尘埃颗粒的可控性整流[13]等现象.尘埃颗粒带电量的测量是尘埃等离子体中一个重要的研究方向.大部分等离子体实验研究的是悬浮在等离子体鞘层附近的微米级尘埃颗粒的带电情况，这些尘埃颗粒通常情况下是带负电的，带电量为102～107e[14].目前，有关极板上较大颗粒的运动以及颗粒的带电情况还未见报道.在极板上，尘埃颗粒可呈现出许多新的物理现象，而为了揭示这些现象背后的物理机制，首先需要搞清楚颗粒的带电情况.

在尘埃等离子体中当2个带电颗粒发生碰撞时，其中任何一个颗粒都可以被看成是探测另一个颗粒的探针去研究另一个颗粒.本文采用一种新的方法，即利用等离子体中带电颗粒的中心弹性碰撞运动，来研究极板上运动的尘埃颗粒的带电量.通过实验可以得到颗粒碰撞的录像，利用图像处理得到颗粒的碰撞轨迹，进而通过2个碰撞颗粒的轨迹就可以得到带电颗粒的电荷量.

1 实验装置

实验在尺寸为200 mm×200 mm×130 mm的真空室中进行，如图1所示.上极板为ITO导电玻璃接地，尺寸为175 mm×130 mm，下极板为不锈钢板接直流电源，尺寸为145 mm×145 mm，两极板间距离为60 mm.实验采用氩气作为放电气体，气压为6～20 Pa，氩气流量为10 mL/min.实验中使用大孔吸附树脂作为介质颗粒，其形状为圆形球体且大小均匀，颗粒半径约为250 μm.在下极板的中心位置上放置一个高为20 mm，直径为65 mm的玻璃圆环，用来约束尘埃颗粒的运动范围.

图1 实验装置示意Fig.1 Schematic diagram of the experimental setup

玻璃圆环内壁表面附近有鞘层存在，鞘层电场进而会影响着颗粒的水平运动.为了尽量减小玻璃圆环鞘层对颗粒水平运动的影响，因此在实验中选择了较大半径的玻璃环(其半径大于鞘层的厚度)，同时在数据分析时选择在玻璃环中心处颗粒碰撞的录像，这是因为圆心处的颗粒除了相互之间作用外，受到玻璃圆环的影响最小.

实验开始前将少数颗粒随机放置在下极板玻璃圆环内，接通电源，放电产生均匀等离子体后，当到达一定的气压时，颗粒将在下极板上做随机运动.在真空室的上方采用一个环形光源来均匀照射颗粒.通过真空室上方的高速相机(最高6 000帧/s)来观察并记录颗粒的运动过程.进一步利用 MATLAB程序对所采集到的图像视频进行处理分析，通过程序对颗粒的运动进行跟踪，可以得到颗粒运动的轨迹、碰撞颗粒的相对速度等参量，进而求得下极板上运动的颗粒的带电量.

2 实验结果

实验中，在一定的气压和电压下接通电源放电产生等离子体后，带电颗粒会在玻璃圆环内进行滚动并会不时地与圆环内壁和其他带电颗粒发生随机的碰撞运动.带电颗粒运动的方向具有随机不确定性，大小会随着实验的电压和气压变化而发生相应的改变，在玻璃圆环中心处颗粒碰撞的速度最大可达到0.2 m/s.

为了减小玻璃圆环鞘层颗粒水平运动的影响，选取了一特定的实验条件下在圆环中心处颗粒碰撞的实验录像.实验的条件为气压6.88 Pa，电压-279 V.通过调节高速相机的曝光时间，最终得到了较为理想的2颗粒碰撞运动轨迹录像，进一步对这一条件下2颗粒的碰撞现象进行了分析.

图2为实验所观察到2带电颗粒发生碰撞某时刻的空间位置，其运动轨迹已给出.利用MATLAB程序对这2个带电颗粒的碰撞过程进行处理，得到了碰撞前后的2颗粒中心间距随时间的变化曲线，结果如图3所示.从图2、3中可以看出2个带电颗粒在发生碰撞时的相对距离略大于颗粒的直径，所以2颗粒在碰撞过程中没有发生直接的接触，这也说明它们所带的电性相同，受到彼此排斥力的作用.

图2 带电颗粒的碰撞轨迹Fig.2 Trajectory of charged particles

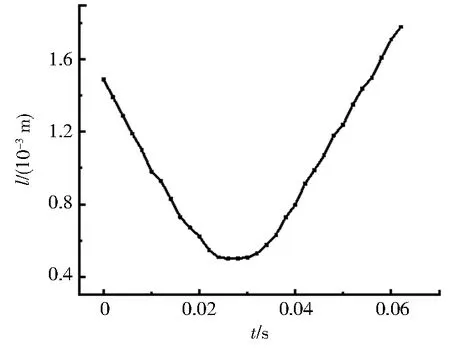
图3 颗粒间距随碰撞时间关系Fig.3 Image of particle spacing changing with time

也就是说其中1个颗粒都处在对应颗粒形成的电场中，因此根据带电颗粒在彼此电场中的受力可以得到

(1)

其中，l是2个颗粒之间的距离；Q为颗粒的带电量；E1、E2分别为2颗粒的场强.在尘埃等离子体中每一个带电颗粒周围都有一个屏蔽库伦势，因此公式(1)可以写成

(2)

其中，r为2带电颗粒中心的相对距离，λ是带电颗粒的屏蔽长度.进一步进行替换使得

A=2πε0mλ3/Q2，y=l/λ，

这样公式(2)可以写成如下公式：

(3)

(4)

其中t0和t是起止时间点，由此可以计算出颗粒碰撞时的相对速度.

图4给出了2带电颗粒碰撞前后相对速度的变化曲线.可以明显地看出，2颗粒在碰撞发生前各自做匀速运动，从t=0.01 s开始，2个带电颗粒受彼此电场相互之间作用发生碰撞，其各自先减速到零之后再反向加速，在t=0.06 s之后2颗粒又以匀速做反向运动，碰撞过程持续约0.05 s.至此，2带电颗粒的碰撞完成并各自在下极板上继续进行随机运动，直至发生下一次碰撞.从图4中也可以明显地看出，2带电颗粒在碰撞前后都做匀速运动，且速度绝对值近似等于0.05 m/s，颗粒在碰撞前后相对速度的方向相反、大小相同，即颗粒体系在碰撞前后动能没有变化.在2颗碰撞达到颗粒间距最小时体系的动能为零，势能达到相应的最大值.因此碰撞前后满足能量守恒定律，2带电颗粒的碰撞为弹性碰撞.

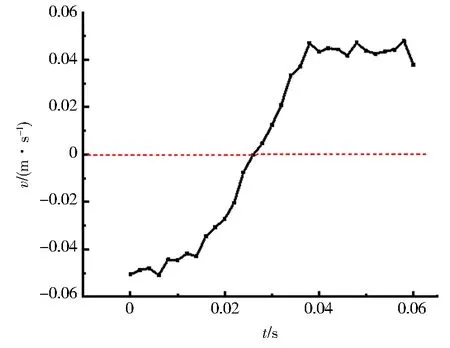
图4 带电颗粒碰撞时相对速度的变化Fig.4 Velocity variation of charged particles in collision

利用带电颗粒的中心碰撞法来计算颗粒带电量[15].该方法要求在颗粒碰撞的轨迹中提取出2个带电颗粒的相对速度和中心距离，而其轨迹与每个颗粒周围的电势分布密切相关.考虑2种电势分布：1)屏蔽库伦势(Yukawa势)；2)库伦势，并分别讨论.

1)首先假设每个颗粒周围都有一个屏蔽的库仑势，这是尘埃等离子体中普遍采用的电势分布

(5)

其中，r为2带电颗粒中心的相对距离；λ是带电颗粒的屏蔽长度.

通过进一步计算可以得出颗粒带电量Q的表达式为[15]

(6)

如前所述，颗粒在碰撞过程中电荷量与屏蔽长度不变，因此，在图5中，不同时刻的系列曲线会存在一个交点，该交点唯一对应颗粒的带电量和屏蔽长度.接下来需要找出屏蔽长度λ为多少时电荷量的相对偏差δQ/Q是最小值便可以得到该交点，进一步利用MATLAB计算出了带电量Q的相对偏差δQ/Q与λ屏蔽长度的关系曲线，如图6所示.在图6中可以看出，带电量的相对偏差随屏蔽长度的增加呈现出先减小后上升的趋势，所以可以很容易地找到带电量相对偏差的最小值即图6中的最低点，该最低点对应的屏蔽长度λc≈0.161 5 mm.得到屏蔽长度λ的值之后，便可以在图5中找到屏蔽长度λc≈0.161 5 mm时颗粒的电荷量Q≈4.375×107e.

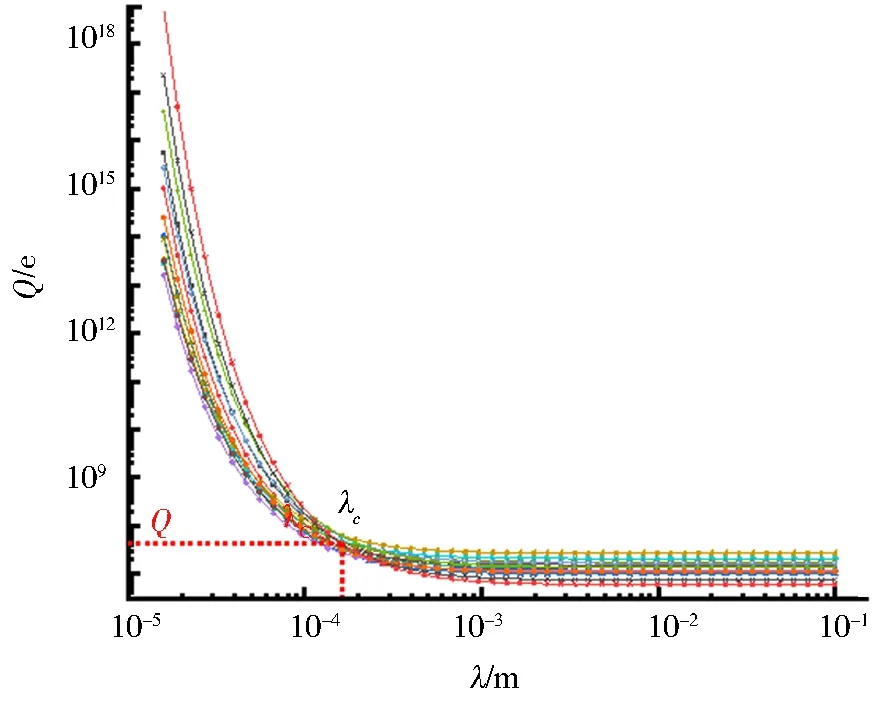
图5 带电量Q随屏蔽长度λ的变化曲线Fig.5 Change curve of the electric charge with the shield length

图6 带电量Q的相对偏差与屏蔽长度λ的关系曲线Fig.6 Relation between relative deviation of charge and the shielding length

2)考虑下极板上带电颗粒之间通过库伦势相互作用

(7)

其中r为2带电颗粒中心的相对距离.通过进一步计算得出带电量Q的表达式为

(8)

式(8)相比于式(6)，并没有出现屏蔽长度λ这个未知量，因此便能够通过实验测得的颗粒相对距离和速度直接确定颗粒的电荷量，在不同时刻电荷量Q的值稳定在同一个数量级，取平均得出Q≈1.398×107e.结果表明在这2种电势分布的情况下，所得到的颗粒带电量的结果相差不大.

3 结论与讨论

利用等离子体中带电颗粒的中心弹性碰撞运动的方法，对直流放电等离子体中下极板上运动的介质颗粒的带电量问题进行了研究.通过分析带电颗粒发生碰撞运动时的碰撞轨迹，得到颗粒运动的相对速度等参量，最终求得颗粒的带电量Q约107e.

众所周知，目前大部分等离子体实验所研究的都是悬浮在等离子体鞘层中的尘埃颗粒，较小的颗粒通常分布在鞘层边界附近，带负电.而大颗粒靠近极板，甚至在极板上，带正电[10].在实验结果分析中对颗粒周围电势的分布考虑了2种情况：1)屏蔽库伦势(Yukawa势)；2)库伦势.分析表明，这2个公式中都有距离r.如前所述，如果将带电颗粒看成是点电荷，需要用2颗粒的球心距离计算，颗粒的带电量Q约107e.如果考虑颗粒的大小，要用2颗粒表面的最近距离计算，其结果减小为点电荷计算时的1/10，带电量Q约106e.在实际过程中需要综合考虑颗粒表面的电荷不均匀分布，r既不是球心距离也不是颗粒表面的最近距离，实际颗粒所带的电荷应该介于这两者结果之间，颗粒的带电量Q为106～107e.