基于直觉模糊多属性决策的逆向物流供应商选择

郭子雪，张运通，田雨，曹秀萌，王子柱

(1.河北大学 管理学院，河北 保定 071002；2.河北大学 图书馆， 河北 保定 071002)

逆向物流是发展循环经济、实现社会经济高质量发展的重要基础和条件，企业加强逆向物流管理，不仅可以减缓环境污染、节约资源，还可以降低成本，增强企业竞争优势，提高企业经济效益.

供应商选择是逆向物流管理的重要组成部分，国内外相关研究主要涉及逆向物流供应商评价指标体系与评价模型的构建2个方面.在评价指标体系构建方面，美国学者Dickson[1]首先通过调查给出了包含服务质量、交货期、历史绩效、资金能力、生产设备和能力、技术能力等23个准则的供应商选择标准；Cleveland[2]建立了包括企业资源实力、管理能力、服务质量、信息技术等4大类指标的物流供应商选择评价体系；李敏等[3]根据逆向物流的特点，从服务水平、联盟性、企业实力、经验和价格5个维度建立了第三方逆向物流供应商选择的评价指标体系；陈春霞等[4]认为构建逆向物流供应商评价指标体系时应考虑综合素质指标、兼容性指标等；曹琳[5]从资源、服务质量、管理水平、信息技术水平、环保水平等5个方面研究了逆向物流供应商选择问题.在评价模型构建方面，Meade等[6]建立了基于ANP的逆向物流供应商选择问题评价模型；Momeni等[7]通过构建多目标可加网络DEA模型，研究了第三方逆向物流供应商效率问题； Li等[8]构建了基于混合信息多准则决策的第三方逆向物流供应商选择模型；贺团英等[9]建立了基于可拓评价法的报废汽车逆向物流供应商选择评价模型；李晓丽[10]、陈可嘉[11]、李娟等[12]分别将粗糙集理论、Gl(改进的主观赋权)法与TOPSIS法(逼近理想解的排序方法)相结合，研究逆向物流供应商选择问题；杨利平等[13]利用基于二元语义的多属性群决策方法，讨论了逆向物流供应商评价与选择问题；王巧玉等[14]通过定义满意度概念，建立了逆向物流供应商选择的多属性评价模型；Govindan等[15]基于ELECTRE I(选择消去)法提出了可持续第三方逆向物流供应商选择途径.本文在相关研究基础上，根据逆向物流供应商选择问题的特点，利用基于信息熵的直觉模糊多属性决策方法研究逆向物流供应商选择问题，希望通过建立逆向物流供应商选择评价模型，帮助企业合理制定逆向物流供应商选择决策.

1 预备知识

1.1 直觉模糊集及其距离测度

(1)

1.2 直觉模糊熵

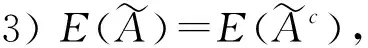
(2)

是一个直觉模糊熵.

1.3 直觉模糊加权集结算子

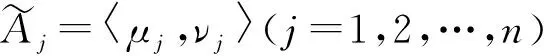
(3)

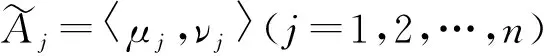
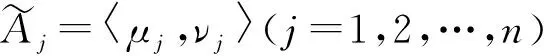
(4)

2 逆向物流供应商选择的直觉模糊多属性决策算法

2.1 问题描述

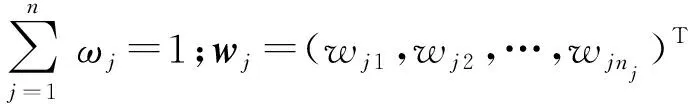
表1 关于准则Bj的直觉模糊决策矩阵Fj

2.2 逆向物流供应商选择的决策步骤

步骤1 构建决策准则Bj下的直觉模糊决策矩阵Fj.确定逆向物流供应商选择问题的备选方案集Y={Y1,Y2,…,Ym}，用直觉模糊数表示各备选逆向物流供应商关于二级指标的评价信息，构建Yi(i=1,2,…,m)关于准则Bj(j=1,2,…,n)的直觉模糊决策矩阵Fj.

步骤2 确定逆向物流供应商选择问题的直觉模糊决策矩阵F.首先利用直觉模糊熵，分别计算准则Bj下的二级指标Cjkj(j=1,2,…,n,kj=1,2,…,nj)的模糊熵Ejkj和权重wjkj：

(5)

(6)

根据直觉模糊加权平均算子(IFWA)，可以计算备选逆向物流供应商在准则Bj(j=1,2,…,n)下的直觉模糊评价值

(7)

步骤3 根据直觉模糊多属性决策矩阵F确定逆向物流供应商选择问题的正理想解Y+和负理想点Y-：

(8)

(9)

步骤4 计算各备选逆向物流供应商Yi(i=1,2,…,m)到正理想解Y+和负理想解Y-的距离.利用直觉模糊熵计算准则Bj(j=j=1,2,…,n)的模糊熵Ej和权重ωj：

(10)

(11)

(12)

(13)

步骤5 选择最优逆向物流供应商.计算各备选逆向物流供应商Yi(i=1,2,…,m)的贴近度

(14)

并利用贴近度ci的大小对备选的逆向物流供应商Yi(i=1,2,…,m)进行排序，ci越大表明Yi离正理想解越近,离负理想解越远，相应的供应商越优.

3 数值分析

3.1 问题描述与评价信息

设某制造企业需要选择1家逆向物流供应商，现有4家供应商Y1,Y2,Y3,Y4作为备选方案，供应商选择指标体系如表2所示.假设该制造企业组织有关专家对4家备选的逆向物流供应商Yi(i=1,2,3,4)关于决策准则Bj(j=1,2,3,4)下的二级指标Cjkj(j=1,2,3,4;kj=1,2,…,nj;n1=n3=n4=4,n2=5)进行评价，各备选逆向物流供应商对各二级指标的满足程度可用直觉模糊数来表示，有关评价结果如表3至表6所示.

表2 逆向物流供应商选择指标体系

表3 关于准则B1的直觉模糊决策矩阵F1

表4 关于准则B2的直觉模糊决策矩阵F2

表5 关于准则B3的直觉模糊决策矩阵F3

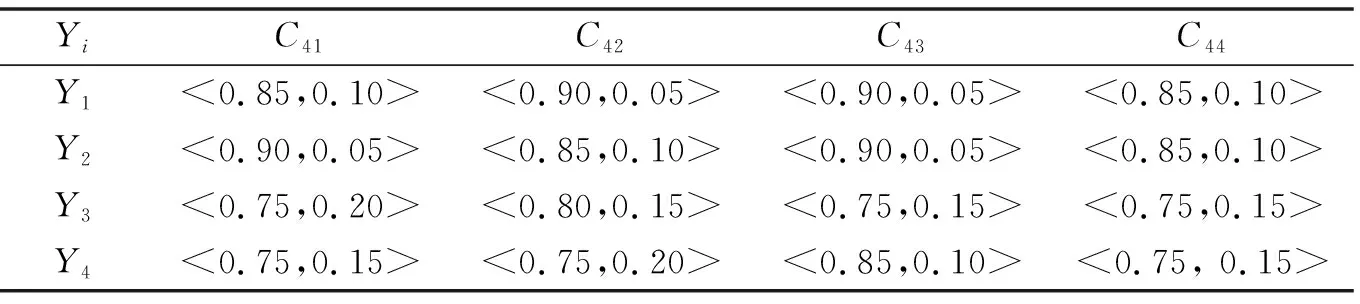
表6 关于准则B4的直觉模糊决策矩阵F4

3.2 方案评价与结果排序

下面用直觉模糊熵-TOPSIS法对4家逆向物流供应商进行评价和选择.

步骤1 计算各二级指标的权重

根据表3至表6，利用式(5)和式(6)计算各二级指标Cjkj(j=1,2,3,4;kj=1,2,…,nj)的权重wjkj，计算结果如表2所示.

表7 逆向物流供应商选择的直觉模糊决策矩阵F

步骤3 确定正理想解Y+和负理想解Y-.由表7可知，其正理想解Y+和负理想解Y-分别为

Y+=(〈0.878,0.090〉,〈0.873,0.078〉,〈0.879,0.075〉,〈0.879,0.052〉),

Y-=(〈0.745,0.189〉,〈0.806,0.142〉,〈0.766,0.146〉,〈0.764,0.161〉).

步骤4 计算决策准则Bj(j=1,2,3,4)的权重.将表7的数据代入式(10)和式(11)，可计算决策准则Bj(j=1,2,3,4)的模糊熵Ej和权重ωj分别为

E1=0.580 0，E2=0.485 3，E3=0.505 7，E4=0.486 8；

ω1=0.216，ω2=0.265，ω3=0.255，ω4=0.264.

表8 备选逆向物流供应商的相对贴近度

由表8可知，4个备选逆向物流供应商的优劣排序为Y1Y2Y3Y4，即逆向物流供应商Y1为最佳.

4 结论

本文将模糊熵、直觉模糊加权平均算子、TOPSIS法相结合，研究了逆向物流供应商选择问题.利用直觉模糊熵确定逆向物流供应商评价指标的权重；运用直觉模糊加权平均算子对二级指标评价信息进行集结，得到逆向物流供应商选择问题的直觉模糊决策矩阵；在此基础上，构建了基于直觉模糊熵-TOPSIS法的逆向物流供应商评价模型，为企业合理选择逆向物流供应商提供了一种可行方法.